自主巡线四旋翼无人机建模及姿态控制器设计

洪世杰，李嘉欣，侯佳木，杜程茂，李忠兵

（西南石油大学电气信息学院，成都 610500）

0 引言

四旋翼无人机是一种具有良好的实用性和发展前景的微型飞行器，可以实现自动悬停、前飞、倒飞等操作[1]。由于具有轻便快捷、成本低、巡航力强等优良的性能，在军事侦察、航空摄影、应急救援、信息获取等方面得以广泛应用[1]。正是由于四旋翼无人机在国防、民用、商用等发展潜力巨大，国内外的科研机构及企业对四旋翼无人机进行了大量研究和开发，如北京航空航天大学、美国宾夕法尼亚大学、中国大疆创新科技有限公司、德国MK公司、法国PARROT公司等。总的来说，目前四旋翼无人机的研究主要体现在基于惯导的自主飞行、基于视觉的自主飞行和自主飞行器系统设计这三个方面。近年来，基于视觉的四旋翼飞行器巡线飞行成为科研工作者研究的热门话题[2-3]。

QUAV的关键技术包括：结构改进、精确数学模型的建立、姿态解算以及控制策略等。然而，QUAV系统具有驱动不足、强耦合、多变量、非线性等特点，其控制器设计存在一定的难度[4]。目前主要提出的控制器主要有：线性二次型最优（LQR）控制器[5]、经典PID控制器[6]、自适应模糊 PID（FPID）控制器[4]、反步控制器[7]及滑模控制器[8]等。经典PID控制器及LQR控制器均为早期研究中提出的基于线性系统的控制理论，具有一定的局限性；FPID控制器参数优化未达到最优；反步控制器运算量较大，影响系统响应的实效性；滑模控制器鲁棒性较好，但容易导致飞行器在飞行中产生抖动[9]。

为了解决QUAV自主巡线飞行及悬停过程中存在的控制精度差、抗干扰能力弱等问题，设计一种新型姿态控制器。分析了QUAV的基本工作原理，建立基于牛顿-欧拉（Newton-Euler）方程的QUAV数学模型，提出一种基于微分进化算法的PID（DE-PID）姿态控制器，搭建仿真及实验对新型姿态控制算法的有效性进行验证。

1 四旋翼无人机数学模型

1.1 QUAV 的基本工作原理

按系统架构分类，可将四旋翼无人机可分为“X”型和“十”型两类。“十”型在调节参数方面比较方便，飞行容易。以“十”型QUAV为研究对象，无刷电机作为动力装置分别对称安装在四轴的末端，QUAV系统结构如图1所示。QUAV的电机可分为两组，前后电机实现顺时针旋转，左右电机实现逆时针旋转。四个以固定角度安装的电机分别代表四个输入力，即每个螺旋桨产生的推力。在保持总推力不变的情况下，俯仰运动是通过增加（降低）后电机的转速，同时减少（增加）前电机的转速后来获得的；增加（降低）右电机的转速，同时减少（增加）左电机的转速以获得翻滚运动；偏航运动可通过增加（降低）前后电机的转速，同时减少（增加）左右电机的转速实现。另外，同时等量增加（减少）四个电机的转速，可实现QUAV的垂直起降运动。

图1 QUAV系统结构图

1.2 QUAV数学模型

四旋翼无人机是具有四输入、六输出的欠驱动的系统，外界干扰输入对稳定性的影响较大，同时，由于其结构复杂使得数学模型的建立存在困难。为建立相对精确的数学模型，需作如下假设：①QUAV视为刚体且具有完全对称结构；②机身重心与两轴交点重合，忽略飞行高度以及地球自转对重力加速度的影响；③飞行过程中机身所受空气阻力视为常数。

为进一步建立QUAV的数学模型，需定义惯性坐标系和机体坐标系，如图1所示。四旋翼无人机的方向由翻滚角φ、俯仰角θ、偏航角Ψ三个欧拉角表示。基于机体坐标系的旋转矢量表示为ΩT=（φ，θ，Ψ）；基于惯性坐标系的位置矢量表示为rT=（x，y，z）。采用变换矩阵R可将机体坐标系转换到惯性坐标系：

式中，SΨ、Sθ、Sφ为取三个欧拉角的正弦值；CΨ、Cθ、Cφ为取三个欧拉角的余弦值。QUAV四个旋翼产生的升力可表示为：

b为升力因素，ωi为第i个电机的转速，其中i=1，2，3，4。则四个旋翼所产生的总升力为：

由Newton-Euler定理得到描述QUAV加速度的微分方程：

由惯性对角矩阵 I（主对角元素为惯量 Ix、Iy、Iz）、

转动惯量IR、描述作用于飞行器机身的转动惯量矩阵M，陀螺力矩惯量MG可以得到下一个微分方程：

其中，向量M表示为：

四个旋翼的旋转速度ωi为QUAV的四个实际速度输入变量，为使变换后的输入变量同样适用于所建立模型。将输入变量重新定义为：

式中，u1为作用于 QUAV 的升力；u2、u3、u4分别为产生翻滚转矩、俯仰转矩、偏航转矩的力。由于陀螺仪扭矩取决于旋翼的旋转速度以及转换后的输入变量uT=（u1u2u3u4），输入变量函数定义为：

结合（4）式和（5）式可以得到QUAV所有的动力学模型如下：

2 微分进化优化算法

式中，randj,i是一个均匀分布的随机数，且randj,i∈（0，1）；,分别为上边界和下边界。

针对给定的参数向量xi,G任意选择三个向量xr1,G、xr2,G和 xr3,G。下标 r1、r2 和 r3 为不同整数且 r1、r2、r3∈（1，2，…，NP）。将 xr2,G、xr3,G的加权差与基本向量 xr1,G求和可得：

变异系数F为0～2之间的常数，可以控制的微分变异的程度；向量vi,G+1即为变异向量。

交叉算子可以融合上一代成功的解决方案，试验向量ui,G+1是由目标向量xi,G的元素和突变向量vi,G+1的元素组成，交叉算子表示为：

微分进化是由Storn和Price提出的一种随机的、基于人群的优化算法，能够优化实参、实值函数，并在求解连续非线性优化问题中具有鲁棒性。微分进化是由初始化和变异、交叉和选择阶段的循环构成，是一种基于种群NP参数向量的并行直接搜索方法[10]。因此，若需优化一个具有D参数的函数，必须先确定种群NP的值。

其中，xi,G是在每一代产生的参数向量；i=1，2，…，NP；j=1，2，…，D；G 表示代数；NP 在最小化过程中保持恒定。在已限制的搜索空间内的一个较高的上边界与较低的下边界之间，所有的参数向量都是被随机初始化（G=0）。初始化形式采用下式：

CR为用户决定的控制参数，被称为交叉率，CR∈[0,1]。Irand 是取自[1，2，…，D]的随机整数，可保证 ui,G+1从vi,G+1中至少得到一个参数。为使迭代过程中vi,G+1的所有元素都在已定义的边界范围内，采用文献[10]所提出的表达式：

目标向量xi,G与试验向量ui,G+1作比较，选择低代价函数值作为下一代：

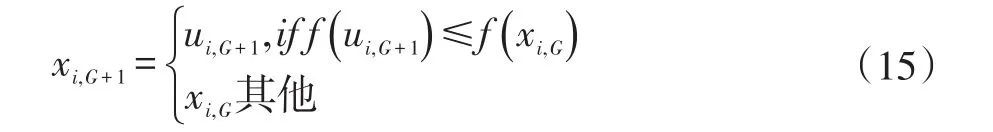
3 姿态控制器设计

微分进化算法被视为解决优化问题的一种高效的技术，可用于QUAV姿态控制器的参数优化。微分进化从包含一系列参数向量的初始种群开始，其中每个参数向量都是问题的解，其性能由适应度函数进行评估。微分进化算法主要由变异、交叉和选择三个基本阶段组成且持续循环直到满足中止条件为止。本文提出一种基于微分进化算法的PID姿态控制器结构如图2所示：

图2中，DE-PID控制器的输入为QUAV姿态角的参考向量（φref，θref，Ψref），输出为 QUAV 的翻滚角、俯仰角和偏航角三个姿态角向量（φ，θ，Ψ）。微分进化算法模块用于优化每一姿态角的PID控制参数（KP,KD,KI）。应用于微分进化算法的适应度函数是通过求取误差的方均根值得到：

式中，N表示在采样时间内所采样的数据个数。

4 仿真与实验

为验证本文提出的DE-PID姿态控制器的有效性，搭建MATLAB/Simulink仿真对姿态控制器性能进行分析，然后搭建QUAV系统实物平台对控制算法进行验证。QUAV实物系统采用DE-PID控制的姿态内环、FPID控制的位置外环的双闭环控制策略。图3为基于视觉的自主巡线QUAV的系统结构图，主控芯片采用STM32F407ARM处理器；图像处理模块由OV707摄像头模块与一片独立STM32F407ARM芯片构成；高度信号采集模块采用HR-SRF05超声波传感器；飞行器姿态角度采集采用MPU-9150传感器实现。

图3 基于视觉的QUAV系统结构图

4.1 仿真结果

针对不同QUAV系统，微分进化算法的参数设定将有所不同。本文仿真参数设置如下：种群量值NP为25，需优化变量个数为9，最大代数为1200，变异因素F=0.7，交叉因素CR=0.3。QUAV系统详细仿真参数如表1所示：

表1 仿真参数

为体现所提出的姿态控制器优越的控制性能，采用自适应模糊PID姿态控制器作为对照。输入阶跃信号时，两种不同控制算法下得到的姿态角PID控制参数如表2所示。图4为输入阶跃信号时姿态控制器的响应曲线，图中红线、蓝线、绿色虚线分别表示DE-PID控制器、FPID控制器下系统的响应曲线及阶跃信号。从图中可以看出，采用两种姿态控制器下系统的超调都较小，能零误差跟随阶跃信号，但是DE-PID控制器的快速性优于FPID控制器。

表2 两种姿态控制器的控制参数

图4 阶跃响应曲线

表3列出了系统的超调量os、上升时间tr、调节时间ts以及稳态误差ess四个性能指标的数值。从表3数据可以看出，DE-PID控制器不但具有FPID控制器稳态误差为零的优势，而且上升时间及调节时间更短。因此，仿真结果验证了DE-PID姿态控制器具有控装置精度高，响应速度更快的优点。

表3 控制器性能指标数值

4.2 实验结果

通过搭建基于STM32F407主控芯片的QUAV实物系统测试可知，四旋翼无人机能保持稳定的飞行姿态定高自主巡线飞行。当遇到如风等外界干扰时，系统将以很快的响应速度及时调整姿态，完成精确的巡线任务。

5 结语

针对四旋翼无人机在自主巡线飞行及悬停过程中存在控制精度差、抗干扰能力弱等问题，提出一种基于微分进化算法的新型PID姿态控制器。仿真和实验结果表明，新型姿态控制算法具有比传统模糊自适应PID控制算法更好的控制性能，采用新型姿态控制器下的QUAV系统在自主巡线飞行过程中具有巡线精度高、响应速度快以及抗干扰性强的优点。

图5 实验结果

[1]刘浩蓬,龙长江,万鹏等.植保四轴飞行器的模糊PID控制[J].农业工程学报,2015,31（1）:71-77.

[2]杨红莉,曾宪阳,杜安国等.飞行器摄像头模块设计及自适应循迹算法研究[J].电子器件,2017,40（6）:1421-1425.

[3]鲁建权,王文虎,成天乐.四旋翼无人机自主循迹算法研究[J].现代计算机,2016,29:14-17.

[4]王健,王承龙,李智等．基于自适应模糊PID的四旋翼飞行器悬停控制[J]．桂林电子科技大学学报,2016,36（5）:406-411.

[5]刘丽丽,左继红.基于ARX模型四旋翼飞行器的LQR控制方法[J].电光与控制,2017,25（8）:1671-4598.

[6]吴成富,刘小齐.四旋翼无人机建模及其PID控制规律设计[J].电子设计工程,2012,20（16）:68-70.

[7]Bouchoucha M,Seghour S,H.Osmani M B.Integral Backstepping for Attitude Tracking of a Quad-Rotor System[J].Electronics and Engineering,2011,116（10）：75-80.

[8]S Bouabdallah,R Siegwart.Backstepping and Sliding-mode Techniques Applied to an Indoor Micro Quadrotor[J].IEEE Conferenceon Robotics an Automation,2005:2247-2252.

[9]王文建,袁亮.四旋翼无人机改进模糊PID姿态控制[J].机械设计与制造,2017,8:9-12.

[10]K.Price,R.Storn,J.Lampinen.Differential Evolution:A Practical Approach to Globle Optimization,Berlin,Germany:Springer,2005.