命题逻辑可满足性问题求解器的新型预处理子句消去方法

宁欣然，徐 扬，陈振颂

(1.西南民族大学 计算机科学与技术学院，四川 成都 610041；2.西南交通大学 系统可信性自动验证国家地方联合工程实验室，四川 成都 610031；3.武汉大学 土木建筑工程学院，湖北 武汉 430072)

0 引言

自动推理是计算机科学和数理逻辑的一个交叉学科，基于命题逻辑的可满足性问题求解和基于一阶逻辑的定理机器证明是自动推理领域中重要且关键的研究内容，其本质是将现实中的问题转化为命题逻辑公式或一阶逻辑公式，通过遵循一定的逻辑推理规则，在逻辑层面判定现实问题是否具有逻辑一致性。大量科学、技术、社会等问题因具有抽象性、复杂性和规模性而无法实现人工逻辑推理与求解，需要采用人工智能手段之一——自动演绎推理自动地进行逻辑推理与求解。当今能够较好地应用自动推理的领域包括软硬件验证领域[19]、专家系统[20]、问答系统[21]、语义网、知识图谱等知识表示和知识推理领域[22-23]、人工智能中的模型推理研究领域[24]和数学定理证明[25-26]等。命题逻辑可满足性问题是逻辑学的一个基本问题，是第一个被证明的NP完全问题[28]，也是当今计算机科学和人工智能研究的核心问题。工程技术、军事、工商管理、交通运输和自然科学研究中的许多重要问题，如智能规划、程控电话的自动交换、大型数据库维护、大规模集成电路自动布线、软件自动开发、机器人动作规划等，均可转化为命题逻辑可满足性问题。

子句集化简一直是命题逻辑表示的可满足性问题求解方法重要的研究方向之一，在当前主流的命题求解器中子句集化简是不可或缺的部分。子句消去方法是简化命题逻辑子句集非常重要的方法，通过删除子句集中的冗余子句，可以简化子句集，加快命题逻辑可满足性问题求解器的求解速度，特别对于由现实问题转化而来的大规模命题逻辑可满足性问题，其子句集中包含有大量冗余子句，如果不进行处理，则可能导致后续命题逻辑求解过程在错误的路径上打转，大量浪费时间和内存，因此在求解初期对这些大规模问题进行简化具有重要的作用。在命题逻辑可满足性问题求解研究初期有一些简单的子句消去方法，例如Davis等[1]提出单元传递和纯文字消去两种简化规则，作为DPLL(Davis-Putnam-Logemann-Loverland)算法[1]回溯时唯一运行的两种规则沿用至今；包含消去(Subsumption Elimination，SE)被嵌入Kowalski连接图中作为删除原则[2]。随后，出现了一些判定条件更加复杂但删除子句范围更广的子句消去方法，例如2010年提出的封锁子句消去方法(Blocked Clause Elimination，BCE)[3]，作为命题逻辑可满足性问题求解器的预处理器，在极大地减少原始命题逻辑子句集规模的同时加快了命题逻辑可满足性问题求解器的求解速度；同年，Heule等[4]将隐藏和不对称概念与著名的子句消去方法——恒真消去方法和包含消去方法结合，发展出新型子句消去方法，包括隐藏恒真消去(Hidden Tautology Elimination，HTE)[4]、隐藏包含消去(Hidden Subsumption Elimination，HSE)[4]、不对称恒真消去(Asymmetric Tautology Elimination，ATE)[4]、不对称包含消去(Asymmetric Subsumption Elimination，ASE)[4]，并分别探讨了这些子句消去方法的规模约简能力、布尔约束传播保持性、约简一致性和逻辑等价性；2012年，Javisalo等[5]再次将归结与文献[4]方法结合，进一步发展出新型子句消去方法，包括归结包含消去(Resolution Subsumption Elimination, RSE)[5]、归结隐藏包含消去(Resolution Hidden Subsumption Elimination, RHSE)[5]、归结不对称包含消去(Resolution Asymmetric Subsumption Elimination, RASE)[5]、归结隐藏恒真消去(Resolution Hidden Tautology Elimination, RHTE)[5]和归结不对称恒真消去(Resolution Asymmetric Tautology Elimination, RATE)[5]。

2017年，Kiesl等[6]将量化布尔公式上的量化蕴涵外部归结式[18]提升到一阶逻辑上，提出一阶逻辑上的蕴涵模归结(Implication Modulo Resolution, IMR)原则，通过该原则将一些命题逻辑上的子句消去方法提升到一阶逻辑上，并给出可行性证明。该文献将IMR原则降到命题逻辑上，提出适应命题逻辑层面的IMR原则，即在子句集F中，若子句C基于其中的一个文字，得到的所有归结式都被F{C}中的子句所蕴涵，则称该子句满足IMR原则。那些看似毫无关联的命题逻辑子句消去方法BCE，RSE，RHSE，RHTE等均在IMR原则之下，因而能将这些子句消去方法进行结合推广，形成新型命题逻辑子句消去方法(BC+RS)E，(RS+RHT)E和(RHS+RHT)E，并给出可行性证明。此外在不同时间限制内，将(BC+RS)E，(RS+RHT)E，(RHS+RHT)E与著名的子句消去方法BCE进行实验对比，结果表明：化简子句数量庞大且结构复杂的子句集时规定的时间越长，新型子句消去方法对化简子句集的效果越好。在同样的限定时间中，当子句消去方法的判定条件难易程度和时间复杂度达到平衡时，子句消去方法的化简能力最好；当化简比较简单的命题逻辑子句集时，有效性越高的新型子句消去方法化简子句集的能力越强，且均优于BCE方法。

1 背景知识

2 命题逻辑上的蕴涵模归结原则

Kiesl等[6]在2017年将量化布尔公式上的量化蕴涵外部归结式[18]提升到了一阶逻辑上，提出一阶逻辑上的蕴涵模归结原则。本文认为该原则同样可以降到命题逻辑上，在该原则框架下提出新型命题逻辑子句消去方法，并保证这些子句消去方法在命题逻辑上具有可行性。本章主要介绍延伸到命题逻辑上的蕴涵模归结原则。

定义2设在子句集F中，若子句C基于文字l(l∈C)与F中的子句归结，得到的所有归结式都被F{C}蕴涵，则称子句C是基于l上的蕴涵模归结子句，满足蕴涵模归结原则。

蕴涵模归结子句的一个特例是子句C中含有纯文字l，因为l是纯文字，子句集中没有文字能够与l归结，所以没有l-归结式，这样的子句C是比较特殊的蕴涵模归结子句。下面的例子展示的是更为一般的蕴涵模归结子句。

蕴涵模归结子句是冗余的，即删除满足这样条件的子句不会影响到子句集本身的不可满足性或是可满足性。在证明蕴涵模归结子句的冗余性之前先证明一个引理。

引理1设子句C是子句集F中基于l(l∈C)上的一个蕴涵模归结子句，指派α满足F{C}中的所有子句，但是弄假子句C。通过翻转指派α对文字l的赋值，保持其他赋值不变，得到指派α′，则指派α′不仅满足子句C，还满足F{C}中所有子句。

定理1设子句C是子句集F中的蕴涵模归结子句，则子句C在子句集F中是冗余的。

证明从引理1可知，若F{C}在一个指派α下是可满足的，则一定可以找到一个指派α′，F在α′下是可满足的。因此F和F{C}是等价满足的。综上，子句C在子句集F中是冗余的。

3 新型子句消去方法

本章讨论命题逻辑上已有的具有蕴涵性质的子句消去方法，并说明这些子句消去方法能够在蕴涵模归结原则的框架下进行组合推广，形成新型子句消去方法。

3.1 具有蕴涵性质的子句

2010年，Heule等[4]基于子句的冗余性质提出多种子句消去方法，这些冗余子句看似相互独立，并不关联，实际上均具有蕴涵性质。本节证明这些这些冗余子句均具有蕴涵性质，为3.2节提出新型子句消去方法做准备。表1所示为子句的各类冗余性质[4]。

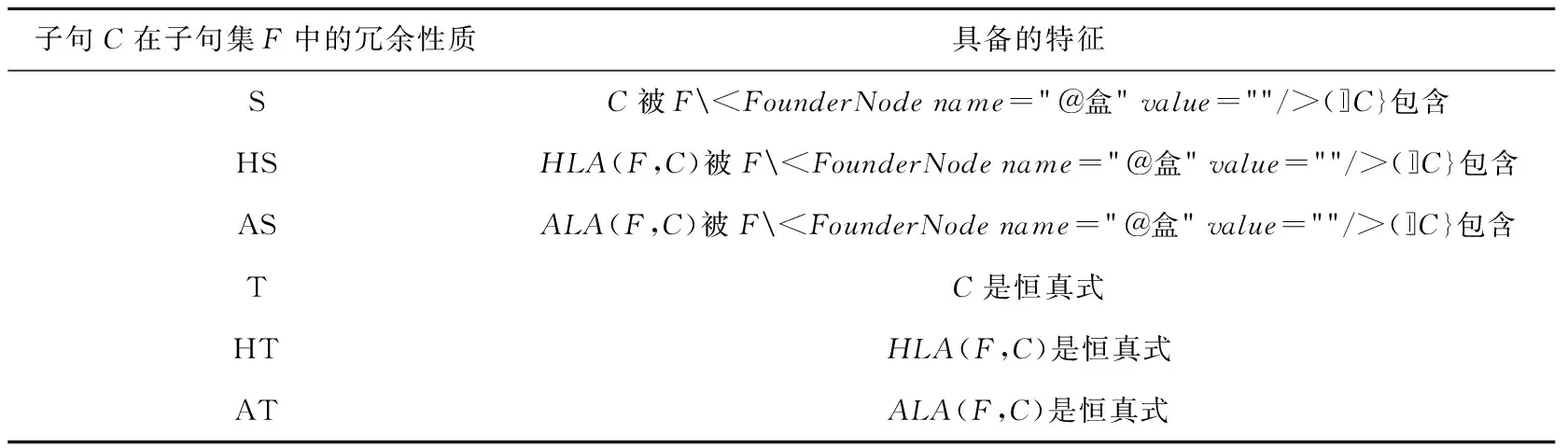
表1 子句的冗余性质说明

表1中的冗余性质有效性的高低如图1所示。图中箭头含义为，若性质A指向性质B，则表示性质A比性质B更为有效。换言之，若一个子句具有性质B，则其一定具有性质A。

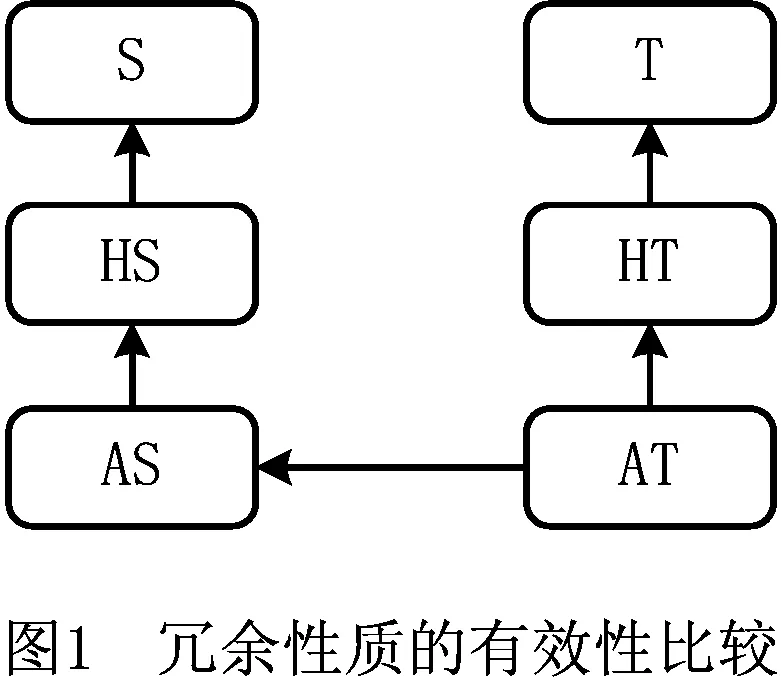
在Heule等[4]提出表1中所展示的子句冗余性质后，Jarvisalo等[5]提出冗余性质的拓展概念，其将归结原则R置于表1中各类冗余性质的前面，得到的性质仍然是冗余性质。简而言之，基于冗余性质P，子句消去方法PE(PE为删除子句集中具有性质P子句的子句消去方法)具有可靠性，则基于性质RP，性质RP是冗余性质，且子句消去方法RPE(RPE为删除子句集中具有性质RP子句的子句消去方法)具有可靠性。根据表1中的冗余性质，扩展的冗余性质如表2所示。

表2 扩展的冗余性质说明

表2中的冗余性质有效性如图2所示[4]。

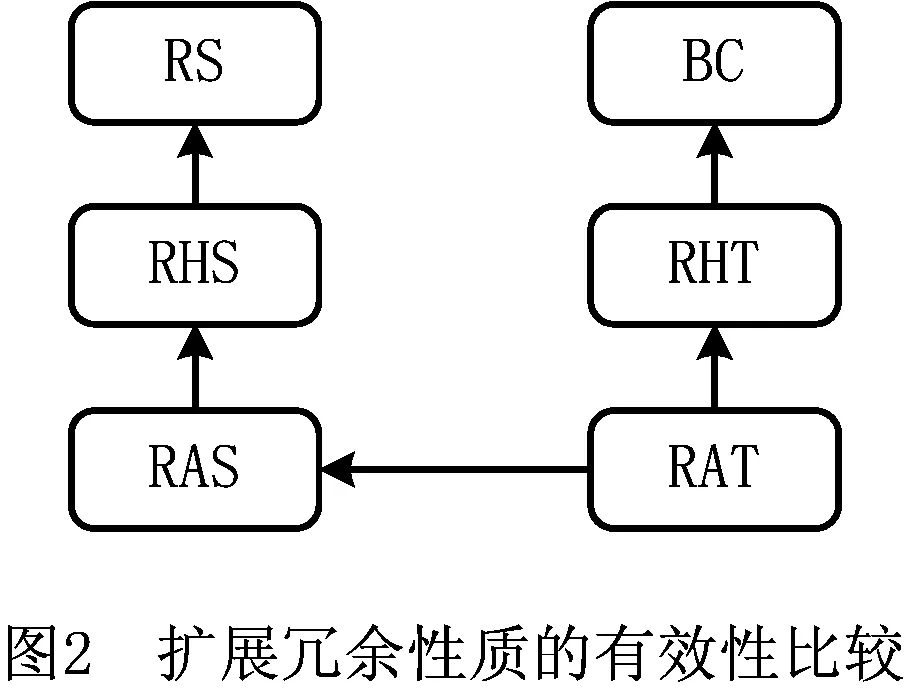
具有表1冗余性质的子句均具有蕴涵性质(被F{C}蕴涵)。当子句C被F{C}包含，则其一定被F{C}蕴涵；子句C是恒真式时，也被F{C}蕴涵。下面证明当ALA(F,C)和HLA(F,C)具有蕴涵性质时，子句C也具有蕴涵性质。

引理2设文字l是子句集F中子句C的不对称文字，则有F{C}(C≡C∨l)。

定理2设子句C是子句集F中的子句，若ALA(F,C)被F{C}蕴涵，则子句C被F{C}蕴涵。

证明假设子句D=ALA(F,C)，则存在一个序列l1,…,ln，其中li是F{C}中子句的文字，li是C∨l1∨…∨li-1的不对称文字，且C∨l1∨…∨ln=D。通过重复应用引理2，有F{C}(C≡C∨l1∨…∨ln)。因为ALA(F,C)被F{C}蕴涵，F{C}(C∨l1∨…∨ln)，F{C}C，所以C被F{C}蕴涵。

定理3设子句C是子句集F中的子句，若HLA(F,C)被F{C}蕴涵，则子句C被F{C}蕴涵。

证明隐藏文字增加可以看作为不对称文字增加的特例，即每一个提供不对称文字的子句均为二元子句。从定理2得知，若ALA(F,C)被F{C}蕴涵，则子句C被F{C}蕴涵。HLA(F,C)作为ALA(F,C)的特例，同样满足定理2，因此若HLA(F,C)被F{C}蕴涵，则子句C被F{C}蕴涵。

定理4若在子句集F中子句C是隐藏包含子句HS或者不对称包含子句AS，则子句C被F{C}蕴涵。

证明设子句C是AS，则子句C的ALA(F,C)子句被F{C}包含，且被F{C}蕴涵。根据定理2，子句C被F{C}蕴涵。当子句C是HS时，子句C的HLA(F,C)子句被F{C}包含；当HLA(F,C)子句被F{C}包含时，HLA(F,C)子句被F{C}蕴涵。根据定理3，子句C被F{C}蕴涵。综上，若在子句集F中子句C是隐藏包含子句HS或者不对称包含子句AS，则子句C被F{C}蕴涵。

定理5若在子句集F中子句C是隐藏恒真子句HT或者不对称恒真子句AT，则子句C被F{C}蕴涵。

证明设子句C是HT子句，则子句C的HLA(F,C)子句是恒真式，被F{C}蕴涵。根据定理3，子句C也被F{C}蕴涵。若子句C是AT子句，则子句C的ALA(F,C)子句是恒真式，被F{C}蕴涵。根据定理2，子句C被F{C}蕴涵。综上，若在子句集F中子句C是隐藏包含子句HT或者不对称包含子句AT，则子句C被F{C}蕴涵。

3.2 新型子句消去方法

从3.1节可知，当子句集F中子句C满足冗余性质S，HS，AS，T，HT或AT时，子句C被F{C}蕴涵。蕴涵模归结原则要求子句C′的所有l-归结式均被F{C}蕴涵，又因为子句C′的每一个l-归结式满足性质S，HS，AS，T，HT或AT，根据定理4和定理5可知子句C′的每一个l-归结式都被F{C}蕴涵，所以若子句C′的每一个l-归结式满足性质S，HS，AS，T，HT或AT，则C′满足蕴涵模归结原则，在子句集F中是冗余的。

定义3设子句C是子句集F中的子句，且文字l∈C。若子句C共有m个l-归结式R1,…,Rm，且满足2个条件：①每一个Ri(1≤i≤m)具有性质Pj∈{P1,P2,…,Pn}；②性质Pi(1≤i≤n)满足“若一个子句C′具有性质Pi，则该子句具有蕴涵性质”。则称子句C拥有性质RP1+RP2+…+RPn。

定理6若在子句集F中子句C基于文字l∈C，具有性质RP1+RP2+…+RPn，则子句C是子句集F中的冗余子句。

证明设子句C在子句集F中基于l∈C共有m个l-归结式R1,…,Rm。因为子句C在子句集F中具有性质RP1+RP2+…+RPn，所以对于任意Ri(1≤i≤m)，有性质Pj∈{P1,P2,…,Pn}。又因为性质Pi(1≤i≤n)满足“若一个子句C′具有性质Pi，则该子句具有蕴涵性质”，所以子句C的所有l-归结式均具有蕴涵性质，根据蕴涵模归结原则，子句C被F{C}蕴涵，从而可得子句C在子句集F中是冗余的。得证。

下面介绍3种有效的新型组合推广子句消去方法，并证明这些新型组合推广子句消去方法比原始子句消去方法更有效。

定理7若在子句集F中，基于l∈C，子句C具有性质BC+RS，则子句C在子句集F中是冗余的。

证明因为子句C基于文字l在子句集F中具有性质BC+RS，所以子句C的所有l-归结式均具有性质T或S，所有l-归结式均被F{C}蕴涵，子句C满足蕴涵模归结原则，子句C在子句集F中是冗余的。

由于(BC+RS)E删除了子句集中的BC+RS子句集，而RSE和BCE分别删除的是子句集中的RS和BC子句集，只需证明BC子句集和RS子句集是BC+RS子句集的真子集，即可证明(BC+RS)E比RSE和BCE更有效。

命题1BC子句集是BC+RS子句集的真子集。

证明若在子句集F中子句C是基于文字l的BC子句，则子句C的所有l-归结式具有性质T。因为BC+RS子句要求所有l-归结式具有性质T或S，所以当子句C的所有l-归结式具有性质T时，子句C也是BC+RS子句。可以得到结论，当一个子句是BC子句时，它也一定是BC+RS子句，然而当一个子句是BC+RS子句，它不一定是BC子句。例如在例2中，子句C是BC+RS子句，但它不是BC子句，因为其中一个l-归结式a∨d∨e不具有性质T。因此，BC子句集是BC+RS子句集的真子集。

命题2RS子句集是BC+RS子句集的真子集。

定理8若在子句集F中，基于l∈C，子句C具有性质RS+RHT，则子句C在子句集F中是冗余的。

证明因为子句C基于文字l在子句集F中具有性质RS+RHT，所以子句C的所有l-归结式均具有性质S或HT，所有l-归结式均被被F{C}蕴涵，子句C满足蕴涵模归结原则，子句C在子句集F中是冗余的。

同样地，子句消去方法(RS+RHT)E比子句消去方法RSE和RHTE更为有效，即在同一个子句集F中相比删除的子句数，(RS+RHT)E比RSE和RHTE相同或者更多。命题3和命题4充分解释了这一点。

命题3RS子句集是RS+RHT子句集的真子集。

证明若在子句集F中子句C是基于文字l的RS子句，则子句C的所有l-归结式具有性质S。因为RS+RHT子句要求所有l-归结式具有性质S或HT，所以当子句C的所有l-归结式具有性质S时，子句C也是RS+RHT子句。可以得到结论，当一个子句是RS子句时，也一定是RS+RHT子句，然而当一个子句是RS+RHT子句时，它不一定是RS子句。例如在例3中，子句C是RS+RHT子句，但它不是RS子句，因为其中一个l-归结式a∨c不具有性质S。因此，RS子句集是RS+RHT子句集的真子集。

命题4RHT子句集是RS+RHT子句集的真子集。

证明若在子句集F中子句C是基于文字l的RHT子句，则子句C的所有l-归结式具有性质HT。因为RS+RHT子句要求所有l-归结式具有性质S或HT，所以当子句C的所有l-归结式具有性质HT时，子句C也是RS+RHT子句。可以得到结论，当一个子句是RHT子句时，它也一定是RS+RHT子句，然而当一个子句是RS+RHT子句时，它不一定是RHT子句。例如在例3中，子句C是RS+RHT子句，但它不是RHT子句，因为其中一个l-归结式a∨b不具有性质HT。因此，RHT子句集是RS+RHT子句集的真子集。

定理9若在子句集F中，基于l∈C，子句C具有性质RHS+RHT，则子句C在子句集F中是冗余的。

证明因为子句C基于文字l在子句集F中具有性质RHS+RHT，所以子句C的所有l-归结式均具有性质HS或HT，所有l-归结式均被F{C}蕴涵，子句C满足蕴涵模归结原则，子句在子句集F中是冗余的。

(RHS+RHT)E子句消去方法也不例外，它同样比其原始子句消去方法RHSE和RHTE更有效。命题5和命题6证明了这一点。

命题5RHS子句集是RHS+RHT子句集的真子集。

命题6RHT子句集是RHS+RHT子句集的真子集。

4 实验结果比较

在规定的不同时间内，比较(BC+RS)E，(RHS+RHT)E，(RS+RHT)E 3种子句消去方法与现有的子句消去方法BCE化简子句集的能力。虽然在理论上，子句消去方法(BC+RS)E，(RHS+RHT)E，(RS+RHT)E均能在同一个子句集中删除更多的子句，比现有的BCE方法更有效，但是在具体实现上，这些子句消去方法的判定条件更复杂，时间复杂度更高，因此在规定的时间内不一定能比BCE删除更多的子句数。实验分为两部分：①针对由规划问题转化而来的子句数量大且结构复杂的命题逻辑可满足性问题，测试这4种子句消去方法的化简能力；②针对简单随机生成的命题逻辑可满足性问题，测试这4种子句消去方法的化简能力。

自从1992年Kautz等[29-30]首次将规划问题求解转化为命题逻辑可满足性问题求解，所建成的black-box规划系统(该规划系统是将规划问题转化为命题逻辑可满足性问题进行求解)在第一届智能规划系统比赛中获得第一名后[31]，越来越多的规划问题被转化为命题逻辑可满足性问题进行求解。然而，由于规划问题为大规模问题，对转化后的命题逻辑子句集进行子句集化简，以提高后续命题逻辑可满足性问题求解器的求解效率，是非常重要的一环。在实验的第①部分选取由规划问题转化而来的命题子句集，测试这些新型子句消去方法对这类特殊命题逻辑子句集化简是否有效。

实验第①部分选取SATLib标准库(https://www.cs.ubc.ca/～hoos/SATLIB/benchm.html)中所有由现实规划问题转化来的命题逻辑可满足性问题，共有11个，其平均子句数为23 261.27个。因为这些子句集子句数量庞大，无法在短时间内找出子句集中所有相关的冗余子句，所以将时间分别限定为0.5 min，1 min，2 min，3 min，4 min，5 min，6 min，7 min，8 min，9 min，10 min，对比各种子句消去方法删除这11个可满足性问题的平均冗余子句数，实验结果如图3所示。

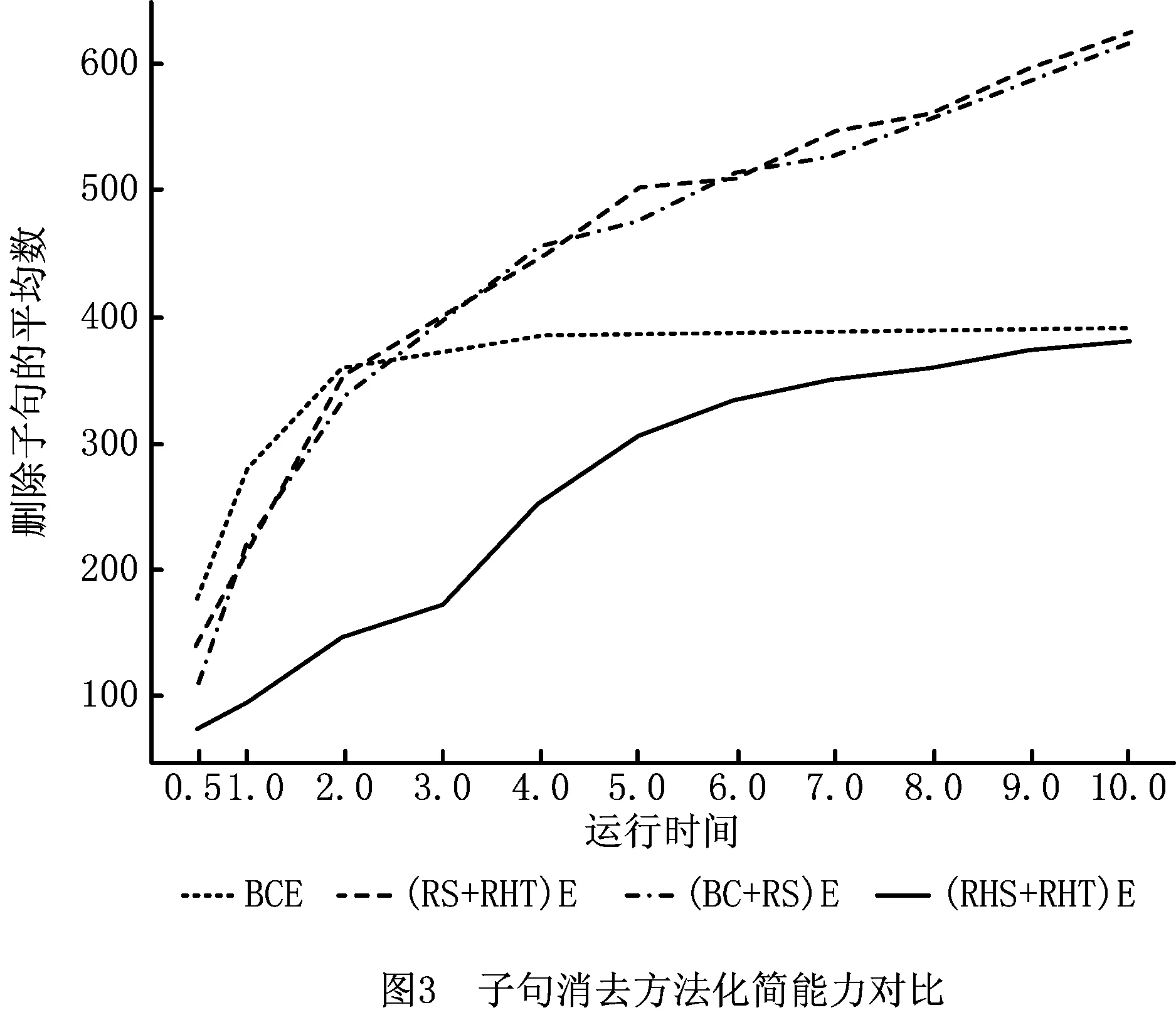
由图3可见，随着限定时间的增加，各类子句消去方法删除子句的平均数逐渐上升。BCE方法的判定条件最简单，能够在较短时间内找到子句集中所有的BC子句，然而由于有效性最低，当限定时间超过4 min时，其删除的BC子句便基本不再增加。虽然理论上(RHS+RHT)E的有效性在4种子句消去方法中最高，但是因为其时间复杂度最高，因此检测到单个RHS+RHT子句的时间最高，所以在限定时间内删除的平均子句数量反而最少。(BC+RS)E和(RS+RHT)E方法的有效性和判定条件的难易程度处于4种子句消去方法的中等水平，其表现最好。当限定时间在2 min内时，这两种方法比BCE删除的平均子句数少，但在2 min后，删除的平均子句数远远超过BCE方法。

从实验结果可知，这些新型子句消去方法化简由规划问题转化而来的命题逻辑可满足性问题是有效的，当化简时间为10 min时，(BC+RHS)E和(RS+RHT)E方法删除的命题逻辑子句集平均超过600个子句，能够较好地化简由规划问题转化而来的命题逻辑可满足性问题。

实验第②部分是测试4种子句消去方法化简随机生成的130个命题逻辑可满足性问题的能力。其中30个命题逻辑可满足性问题包含100个子句、40个变量，另100个命题逻辑可满足性问题包含500个子句、200个变量。由于这130个命题逻辑可满足性问题比较简单，4种子句消去方法均能在较短时间内找到所有冗余子句。表3所示为4种子句消去方法删除130个问题子句的平均数。

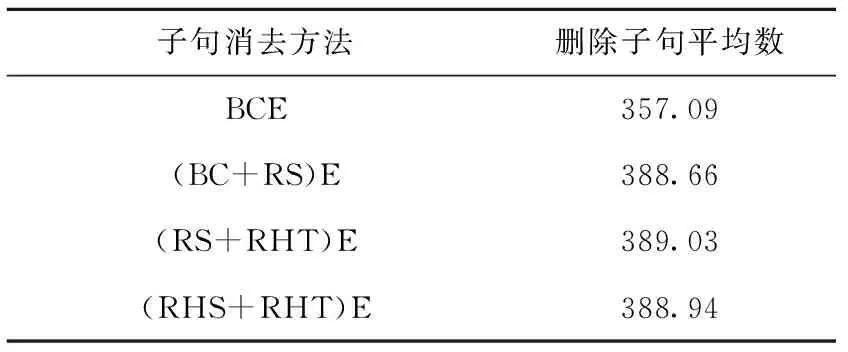
表3 各子句消去方法删除子句的平均数

从表3可见，3种新型子句消去方法化简较为简单的命题逻辑子句集的能力均比BCE方法更强。一般来说，子句消去方法的有效性越高，能够删除的平均数量越多，但是并不是所有子句消去方法都满足这一规律。例如，(RHS+RHT)E比(RS+RHT)E更为有效，但是(RHS+RHT)E删除的平均数反而比(RS+RHT)E更少，原因在于这3种新型子句消去方法均不具有confluence性质，即删除子句的顺序不同，导致最后能够删除的子句数量可能不同。实验依次简单地判断子句集中的子句是否为冗余子句，是则删除该子句，否则保留该子句，然后继续判断下一个子句。

5 结束语

本文将一阶逻辑上的蕴涵模归结原则扩展到命题逻辑上，根据该原则将已有命题逻辑上的子句消去方法进行组合推广，提出比原始子句消去方法更有效的新型子句消去方法，并证明了这些新型子句消去方法的可行性，即利用这些子句消去方法化简子句集，得到的新子句集和原始子句集具有等价满足关系，即新子句集与原始子句集同时具有可满足性或者不可满足性。最后，将新型子句消去方法(BC+RS)E,(RS+RHT)E，(RHS+RHT)E与著名的BCE方法进行实验分析和比较，得到：当化简由规划问题转化而来的子句数量庞大的命题逻辑可满足性问题时，随着限定时间的增加，各种子句消去方法删除的子句平均数据均在增大。在这4种子句消去方法中，表现最好的是(RS+RHT)E和(BC+RS)E方法，其能较好地平衡判定条件的复杂度和有效性，在限定时间为10 min时，能够平均删除由规划问题转化而来的命题逻辑子句集超过600个子句，这两种子句消去方法对化简由规划问题转化而来的命题逻辑子句集是有效的；在化简较为简单的命题逻辑可满足性问题子句集上，3种新型子句消去方法均比BCE方法更强，而且子句消去方法的有效性越高，删除子句的平均数越多。

本文只初步实现了各类子句消去方法，这些方法不具有confluence性质，如果删除子句的顺序不同，则最后得到的新子句差别会很大，本文算法只简单地按照子句集中子句的顺序依次判断子句是否为冗余子句，因此算法仍有很大的改进空间。未来研究将根据这些子句消去方法的特性制定相应的优化策略，进一步提高子句消去方法针对子句数量较大和结构较复杂子句集的化简能力，以期将这些子句消去方法作为命题逻辑可满足性问题求解器的预处理方法来简化子句集，使后面的求解更加高效。