基于Workbench的直齿轮模态与谐响应分析

2018-07-05张小辉孙长青

沈阳工程学院学报（自然科学版） 2018年2期

王超，张小辉，孙长青

(沈阳工程学院 a.工程实训中心；b.机械学院，辽宁沈阳 110136)

随着高、精、尖机器的飞速发展，对传动系统的要求越来越高。齿轮传动是机器传统系统的主要形式，其啮合的动态性能对机器性能起着关键作用。为降低齿轮的失效形式，研究齿轮接触的动力学分析就显得非常重要。齿轮啮合工作中，在外界因素和自身性能的激励下将发生振动现象。振动系统的固有频率和固有振型是其动态特性的关键因素，通过模态分析得出齿轮啮合的固有频率和振型变化是研究机器避免发生共振的基础，从而提高机器运转的工作效率和寿命。齿轮啮合过程中，轮齿会受到载荷冲击，在不同载荷激励下，轮齿的受损程度不同。轮齿结构在受到不同频率沿正弦变化载荷作用下，得到应力、应变的频率响应曲线，为进一步研究齿轮特性提供参考。

齿轮啮合是一种复杂的接触过程,因为作用力的改变而成为一个非线性问题。传统的理论分析是建立在弹性力学的基础上,利用赫兹公式求解齿轮啮合过程的应力和应变值，求解过程是建立在很多假设的理想情况下，结果不够准确。齿轮工作过程中会产生应力、应变和变形，为保证其正常工作需要对齿轮的轮齿和整体受力进行分析，保证其强度和刚度的要求。因此，采用ANSYS软件对齿轮进行模态分析和谐响应分析，并与理论分析进行对比，ANSYS分析则具有直观、准确、快速方便等优点。

1 建立分析模型

对于齿轮啮合运动的分析较为复杂，可以转化为振动学模型。齿轮传动是较为简单扭转振动模型，可等效转化为单自由度系统的振动，如图1所示。

图1 齿轮啮合单自由度模型

单自由度无阻尼系统的运动微分方程：

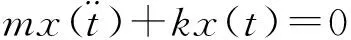
(1)

wn是自由振动系统的自然频率：

(2)

Tn是自由振动的固有周期：

(3)

fn振动频率：

(4)

由运动模型分析可知，综合刚度kv是随时间变化的函数，也是齿轮啮合所受到的刚度激励，齿轮啮合系统的固有频率公式：

(5)

以X6132铣床为例，机床电机额定功率为P=7.5 kW ，输出转速为n=1 440 r/min，主动齿轮材料为20 Cr，从动齿轮材料为40 Cr，如表1所示。

P=T×n/9 550

(6)

圆周力：

Ft=2T/d

(7)

径向力：

Fr=Ft×tanα

(8)

法向力：

Fn=Ft/cosα

(9)

由公式求得：Ft=1 275.37 N，Fr=464.24 N

表1 直齿轮的几何参数

2 基于 Proe/E的参数化建模及模态仿真

2.1 建立有限元模型

根据Proe/E软件的参数化曲线方程准确建立齿轮三维模型，对其进行啮合装配及仿真，保存副本IGES格式，然后导入到Workbench环境中。

2.2 定义材料属性

主动齿轮材料为20 Cr，从动齿轮材料为40 Cr，弹性模量为E=2.06×1011Pa，泊松比为μ=0.3，ρ=7.8×103kg/m3。

2.3 导入模型及网格划分

对于三维实体来说，Meshing网格划分方法分为Automatic、Tetrahedrons、Hex Dominant、Sweep、MultiZone和Inflation。Automatic是最简单的划分方法，但不够精确；Tetrahedrons划分网格可以快速自动生成，对于较复杂的实体，在关键区域可使用曲度和近似尺寸功能自动细化网格，比较精确，单元和节点合适，计算时间合理；Hex Dominant划分网格比较精确，但计算时间较长；Sweep、MultiZone和Inflation网格划分方法比较复杂。结合实际，采用Tetrahedrons划分方法。

通过Geometry命令导入模型，生成实体模型，根据网格划分方法选择Tetrahedrons四面体网格划分，共生成17 047个单元，31 988个节点，如图2所示。

2.4 施加载荷及约束

对两个齿轮施加Fixed Support，选取内孔的4个半圆面，为节约计算时间，选取齿轮啮合部分施加载荷Ft、Fr，从动齿轮受到反向的载荷。

图2 模型划分网格

2.5 模型求解及后处理

研究对齿轮施加预应力的模态分析，图3为前8阶模态总变形分析云图。

2.6 模态结果及分析

通过分析得到前8阶固有频率和固有振型。对于低频响应来说，高阶模态影响不大，可以忽略。为了减小工作量，得到真实的结果，只求解前8阶低频模态结果。对前8阶模态总变形分析云图进行分析，可得出齿轮在固有频率激励下振型的变化情况，如表2所示。

图3 前8阶模态总变形分析

在固有频率为0～2 468.5 Hz和4 646.4 Hz的激励下，齿轮啮合过程稳定，不会发生共振现象。在2 809.4～4 487.2 Hz的激励下，齿轮啮合发生弯曲和扭转变形；在6 392.4～7 063.1 Hz的激励下，齿轮发生复杂变形。因此，轮齿发生共振可能性最大的振型是弯曲变形。

表2 齿轮模态分析前8阶固有频率和振型特征

3 谐响应分析

谐响应分析是计算在齿轮啮合过程中几种不同频率下的响应，得出位移对频率的曲线图，从图中找到峰值，进一步分析在此频率下的应力值。为设计人员提供齿轮结构的动力特性，通过增加阻尼防止发生共振现象的发生。

在谐响应分析中，齿轮啮合的所有节点都在相同频率、不同相位下运动；结构中，阻尼值的差异导致了相位不同。

3.1 谐响应基本方程

ANSYS 计算动力学的基本方程为

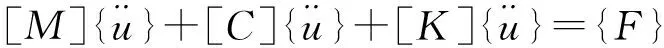
(10)

在谐响应分析中，结构中所有节点以同频率、不同相位运动，位移表达式为

{u}={umaxeiΦ}eiΩt

(11)

式(11)中，umax是最大位移;Ω是强迫频率;φ是位移相位偏量，力矢量表达式为

{F}={Fmaxeix}eiΩt

(12)

将式(11)和式(12)带入式(10)中，得谐响应求解方程如下：

(-Ω[M]+iΩ[C]+[K])({u1}+
i{u2})={F1+F2}

(13)

3.2 后处理及分析

单击Frequency Response，得到节点随频率变化的位移和相角曲线，如图4所示。修改Damping Controls值为0.05，得到节点随频率变化位移和相角曲线，如图5所示。

在4 500 Hz的载荷下，主动齿轮内圈处的(Von-Mises)Stress最大，最大应力值为13.441 MPa。机床齿轮箱内的齿轮材质差异性较大，修改Damping Controls 值为0.05后，在4 500 Hz激励下，齿轮内圈处的(Von-Mises)Stress还是最大且激励频率也没有发生变化，最大应力为5.950 2 MPa。因为阻尼系数的变化，最大应力值差异性很大。所以，通过谐响应分析，可以采用增加阻尼的方式来改变在相同激励载荷作用下的最大应力值，从而避免发生共振，提高齿轮制造性能，延长使用寿命。