基于混合粒子群算法优化BP神经网络的机床热误差建模
2018-07-05,
,
(1.重庆科创职业学院 信息与机电学院,重庆 402160; 2.西南交通大学 机械工程学院,成都 610031)
机床的精密加工技术可以提高市场的竞争力,也是未来加工产业发展的必然趋势.根据市场统计数据,中国是世界最大的数控机床进口国家[1].因此,研究高精密加工的数控机床已经成为中国研究的重要课题之一.当前,数控机床对于精度要求,不仅仅是满足机械的几何精度和运动精度,在机械产品加工过程中产生的摩擦热、切削热及环境温度的变化,都会导致机床、刀具及工件发生变形,引起主轴运动轨迹发生偏差,从而造成工件精度下降.大量研究表明,热误差是影响机床加工误差的主要来源,占总误差的70%左右[2].而导致机床热误差的重要原因是机床主轴旋转产生的热变形.因此,建立机床热误差预测模型,对于改善机床加工精度具有重要意义.
随着机床热误差的深入研究,产生了许多理论和方法.例如:文献[3]采用遗传算法优化BP神经网络,建立机床热误差预测模型,给出遗传算法优化BP神经网络,通过实验验证预测模型的精度,提高了寻优速度;文献[4]采用模糊C均值聚类法筛选温度测量值,通过径向基函数(RBF)建立热机床误差预测模型,通过实验对预测模型进行评价,降低了温度测量数据;文献[5]采用多元线性回归理论,建立机床热误差预测模型,选择机床上敏感温度点,通过多元线性回归理论对温度点进行拟合,提高了机床热误差补偿的精度和效率.以往研究的机床热误差预测模型预测精度较低,造成机床主轴加工误差较大.针对误差较大问题,本文采用混合算法优化BP神经网络参数,将优化后的BP神经网络用于机床热误差预测.在优化过程中,引用了改进粒子群算法和遗传算法,建立了BP神经网络结构简图模型,设计了混合算法优化BP神经网络流程图,通过具体实验,将混合算法优化的BP神经网络用于机床热误差模型预测,将预测结果用于机床热误差补偿,为提高机床加工精度的研究提供了理论依据.
1 混合粒子群算法
粒子群算法通过初始化随机产生一群粒子,每个粒子采用位置、速度及适应度值来表示其特征.粒子在求解空间中移动,通过对比个体极值、群体极值来改变自身的位置和速度.粒子的位置和速度更新方程式[6]为Vt+1=ωVt+c1r1(Pt-Xt)+c2r2(Pt-Xt)
Xt+1=Xt+Vt+1
(1)
式中:ω为惯性权重系数;c1,c2为速度更新参数;r1,r2为随机数,其取值范围为[0,1].
标准粒子群算法,其惯性权重系数ω通常采用线性递减方式,导致粒子陷入局部最优值范围内,也造成全局搜索的难度.对此,采用S形函数改进惯性权重系数,使粒子寻优效果更好.改进惯性权重计算方程式[7]为
(2)
式中:ωmax,ωmin分别为最大和最小惯性权重系数;t,T分别为当前和最大迭代次数;e为速度变化调节系数.
随着粒子群迭代次数的增多,粒子与粒子的相似度就会增强.改进惯性权重系数在一定程度上缓解了各个粒子间的相似度,但是很难避免.对此,在改进粒子群算法的基础上增加遗传算法中的交叉和变异操作,从而快速地搜索出全局最优解.
交叉操作是把个体优秀值和群体优秀值进行交叉,从而获取更优秀的个体.第m个个体最优染色体Am和第n个群体最优染色体An交叉操作方程式[8]为
(3)
式中:r为随机数,r∈[0,1];k为实数编码位数.
变异操作是保持种群的多样性,主要是对自身进行变异操作,从而得到更优秀的个体,选择出最优个体进入下一次迭代中.第i个个体第j个基因变异操作方程式[8]为
(4)
f(t)=1-r(1-t/T)a
(5)
式中:Amax和Amin分别为Aij上界和下界.
2 优化BP神经网络
2.1 BP神经网络
BP神经网络是一种按误差反向传播算法训练学习的多层前馈网络,非线性能力较强,目前采用较为广泛.BP神经网络拓扑结构包括输入层、隐含层、输出层3个部分[9-10],其网络结构如图1所示.在图1中,Xi代表输入值,Yj代表输出值,Wij代表输入层与隐含层连接权值,Wjk代表隐含层与输出层连接权值.
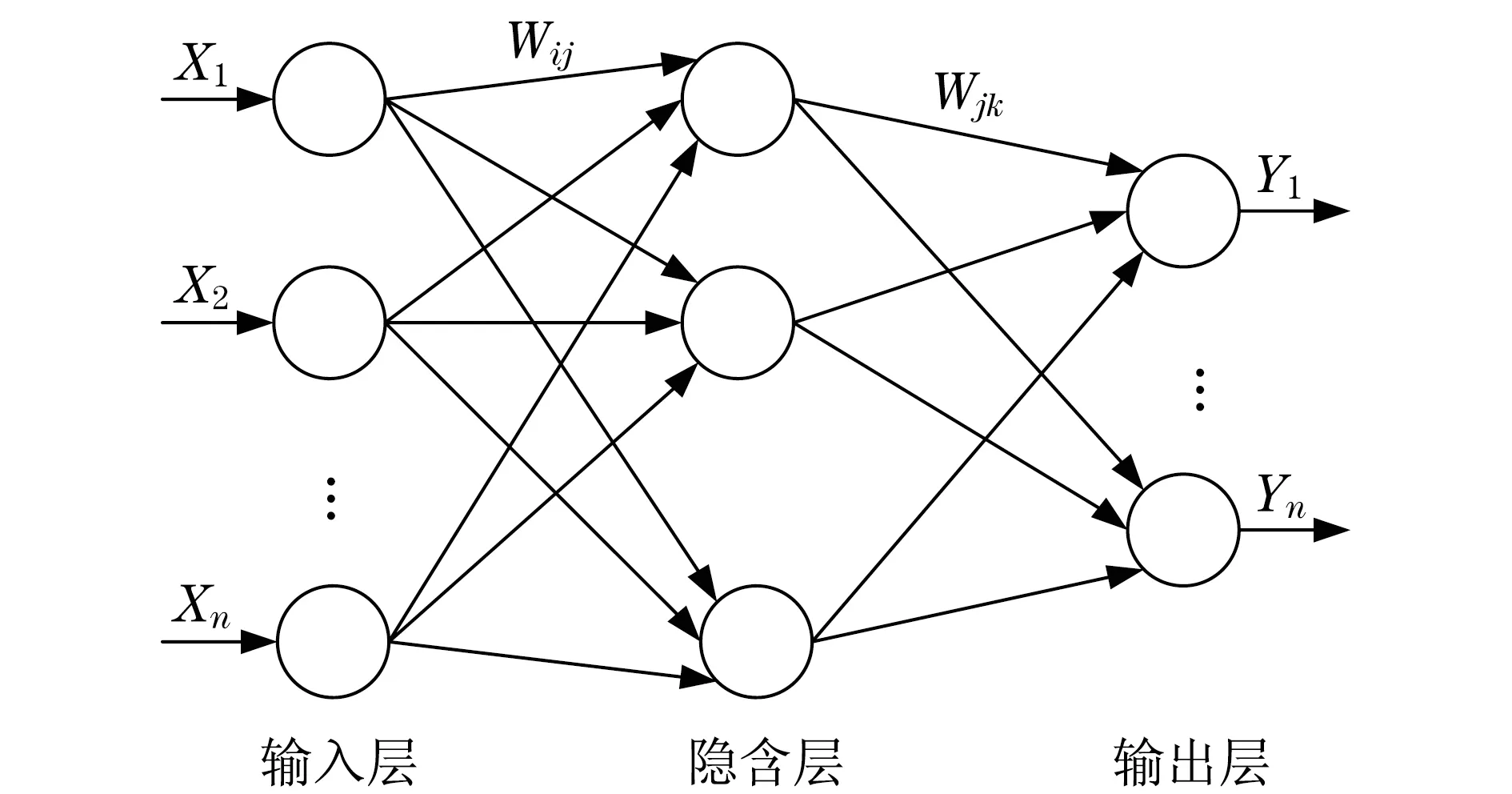
图1 BP神经网络结构简图Fig.1 BP neural network structure diagram
2.2 混合算法优化BP神经网络结构
采用混合算法优化BP神经网络结构,不仅可以搜索到全局最优解,还能够克服BP神经网络结构的不足.混合算法优化BP神经网络结构,采用BP神经网络结构误差平方和的倒数为机床热误差目标函数,其方程式[11]为
(6)
式中:E为机床输出热误差;yi为网络第i个实际值;y′i为网络第i个期望值.其优化流程图如图2所示.

图2 BP神经网络寻优流程图Fig.2 BP neural network search flow chart
3 结果与讨论
3.1 选择温度测量点
采用三轴立式铣床对机床热误差进行测试研究,温度传感器在机床的分布位置如图3所示.主轴转速设置范围为2 000~3 000 r/min之间.在图3中,铣床主轴上安装6个温度传感器用来测试机床运行过程的温度参数,其中,T1在横梁上,T2,T3在铣床主轴上,T4,T5,T6在刀具附近位置.
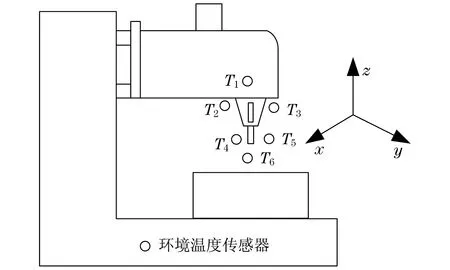
图3 铣床温度传感器位置分布图Fig.3 Position distribution of temperature sensor of milling machine
在实验过程中,外界环境温度为25 ℃,主轴转速以2 000 r/min运行120 min,然后改变主轴转速,以3 000 r/min运行180 min,每5 min测试一次数据,连续测试60组温度数据,实验测试过程如图4所示.

图4 热误差实验过程Fig.4 Thermal error experiment
3.2 BP神经网络热误差预测结果
实验测量温度值作为BP神经网络模型的输入,分别以y轴、z轴方向产生的热误差为目标函数的输出,其预测模型如图5所示.
将连续测试60组温度数据分成两大模块:第1模块为45组,用作训练数据;第2模块为15组,用作测试数据.BP神经网络学习过程中,参数设置如下:学习率为0.02,输出层误差为10 μm,训练迭代次数最大值为300,采用BP神经网络热误差预测y轴、z轴方向结果分别如图6和图7所示.
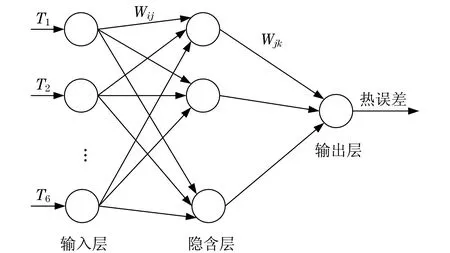
图5 BP神经网络预测模型Fig.5 BP neural network prediction model
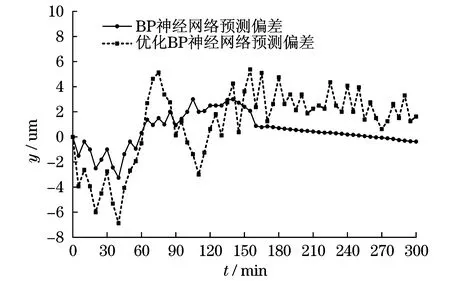
图6 y轴方向预测偏差Fig.6 y-axis direction prediction deviation

图7 z轴方向预测偏差Fig.7 z-axis direction prediction deviation
同理,将连续测试60组温度数据分成两大模块:第1模块为45组,用作训练数据;第2模块为15组,用作测试数据.混合算法优化BP神经网络学习过程中,参数设置如下:学习率为0.02,输出层误差为10 μm,初始种群大小为100,交叉概率为0.1,变异概率为0.02,迭代次数最大为300.采用混合算法优化BP神经网络热误差预测y轴、z轴方向结果分别如图6和图7所示.
3.3 对比与分析
由图6和图7预测模型可知,BP神经网络预测模型预测数据值波动较大,与实验测量值偏差较大,在y轴方向预测误差最大值为6.9 μm,在z轴方向预测偏差最大值为6.7 μm,预测偏差在7.0 μm以内.而混合算法优化BP神经网络预测数据值波动较小,与实验测量值偏差较小,在y轴方向预测偏差最大值为3.3 μm,在z轴方向预测偏差最大值为3.5 μm,预测偏差都在4.0 μm以内.因此,混合算法优化BP神经网络,可以提高热误差预测精度,及时进行热误差补偿,降低机床加工零件产生的误差.
4 结论
本文采用混合算法优化BP神经网络,将优化后的BP神经网络模型用于机床热误差预测,主要结论如下:
(1) 在改进粒子群算法的基础上增加了遗传算法,能够避免单一算法在优化过程中陷入局部最优解.
(2) 优化BP神经网络预测模型,能够降低机床热误差的理论与实际偏差,预测精度较高.
(3) 优化后的BP神经网络,不仅可以用于机床热误差模型预测,而且可以将混合算法优化BP神经网络结构扩展到其他学科优化问题中.
参考文献:
[1] 李世龙.数控机床可靠性评估及分配技术的研究[D].重庆:重庆大学,2013.
LI S L.Research on reliability assessment and allocation technology of CNC machine[D].Chongqing:Chongqing University,2013.
[2] 刘征文.铣车复合加工中心整机热变形及误差补偿的研究[D].兰州:兰州理工大学,2013.
LIU Z W.Research on thermal deformation and error compensation of the milling-turning compound machining center[D].Lanzhou:Lanzhou University of Technology,2013.
[3] 任小洪,徐卫东,刘立新,等.基于遗传算法优化BP神经网络的数控机床热误差补偿[J].制造业自动化,2011,33(5):41-43.
REN X H,XU W D,LIU L X,et al.Thermal error compensation on CNC machine tools based on GA-BP neural network[J].Manufacturing Automation,2011,33(5):41-43.
[4] 苏铁明,叶三排,孙伟.基于FCM聚类和RBF神经网络的机床热误差补偿建模[J].组合机床与自动化加工技术,2011(10):1-4.
SU T M,YE S P,SUN W.Thermal error compensation modeling based on fuzzy C means clustering algorithm and RBF neural network modeling[J].Modular Machine Tool and Automatic Manufacturing Technique,2011(10):1-4.
[5] 田国富,胡军,郭玉学.多元线性回归理论在数控机床热误差补偿中的应用[J].机械工程与自动化,2013(2):128-130.
TIAN G F,HU J,GUO Y X.Application of multiple linear regression theory in thermal error compensation of CNC machine tool[J].Mechanical Engineering and Automation,2013(2):128-130.
[6] ABDULSHAHED A M,LONGSTAFF A P,FLETCHER S.A cuckoo search optimisation-based grey prediction model for thermal error compensation on CNC machine tools[J].Theory and Application,2017,7(2):146-155.
[7] MA C,ZHAO L,MEI X S,et al.Thermal error compensation of high-speed spindle system based on a modified BP neural network[J].The International Journal of Advanced Manufacturing Technology,2017,89(10):3072-3084.
[8] 付涛,弓清忠,王大镇,等.基于ANN模型和HPSO算法的数控机床可靠性分布模型研究[J].四川大学学报(自然科学版),2015,52(2):263-265.
FU T,GONG Q Z,WANG D Z,et al.Numerical control machine reliability distribution model researchbased on the ANN model and HPSO algorithm[J].Journal of Sichuan University (Natural Sciencc Edition),2015,52(2):263-265.
[9] HUANG Y Q,ZHANG J,LI X,et al.Thermal error modeling by integrating GA and BP algorithms for the high-speed spindle[J].The International Journal of Advanced Manufacturing Technology,2014,71(10):1669-1675.
[10] LIANG R J,YE W H,HAI Y,et al.The thermal error optimization models for CNC machine tools[J].The International Journal of Advanced Manufacturing Technology,2012,63(10):1167-1176.
[11] 魏效玲,张宝刚,杨富贵,等.基于GA-BP 网络的数控机床热误差优化建模研究[J].组合机床与自动化加工技术,2016(12):100-102.
WEI X L,ZHANG B G,YANG F G,et al.Research on optimization modeling of CNC machine tools thermal error based on GA-BP neural network[J].Modular Machine Tool and Automatic Manufacturing Technique,2016(12):100-102.
