粒子群算法优化的双臂机器人模糊逻辑控制仿真研究

,

(1.廊坊燕京职业技术学院 机电工程系,河北 廊坊 274015; 2.北京工业大学 电子信息与控制工程学院,北京 100124)

当前,单臂机器人主要应用于焊接、冲压、贴片及喷涂等许多制造行业[1].但是,在高精度装配和复杂工作领域内,单臂机器人很难满足工作的需要.对此,需要使用双臂机器人替代单臂机器人完成复杂任务.双臂机器人执行复杂工作任务具有以下优点[2]:① 使用灵活,可以取长补短;② 扩大工作范围,提高工作效率;③ 具有双重特性,能更好实现人机交互功能.因此,双臂机器人是未来研究和发展的方向.

伴随计算机和电子通讯业的快速发展,研究者对机器人控制也做了许多研究.例如:文献[3]设计了双臂机器人的硬件系统和软件系统,采用单片机技术设计机械臂控制器,根据编码器控制指令实现机械臂的速度、位置及正反转的控制,从而满足机械臂定位控制的要求.文献[4]设计了双臂机器人神经网络PID控制方法,通过在线调节神经网络加权系数,实现3层BP网络性能的最优化,建立神经网络PID控制系统的仿真图,对控制系统运动轨迹进行了仿真验证.文献[5]设计了鲁棒自适应反演控制算法,根据机器人位置和速度误差的反馈,通过神经网络对误差的在线学习,从而实现机器人运动轨迹的自适应控制,控制精度较高.然而,双臂机器人在与外界环境交互过程中,存在外部不确定性的干扰和突变问题,使得双臂机器人很难按照预定轨迹进行运动.针对以上问题,本文建立双臂机器人复杂非线性动力学模型,引用模糊逻辑控制理论,针对控制系统的不稳定性,采用粒子群算法对模糊控制系统进行优化.采用Matlab软件对双臂机器人运动轨迹进行动力学仿真,并与传统PID控制系统仿真结果进行比较,为深入研究双臂机器人运动精度和抖动问题提供了理论基础.

1 双臂机器人模型

机器人手臂具有复杂的非线性动力学,从而增加了精确和稳定控制的难度.为了验证改进模糊逻辑控制性能,选取双臂机器人简图模型为研究对象(见图1).双臂机器人动力学通常采用非线性微分方程表示,建立双臂机器人的动力学方程为[6]

(1)

式中:D(θ)为正定惯性对称矩阵;C(θ,θ′)为向心矩阵;G(θ)为重力矢量;τ为控制输入力矩;θ为转动关节的关节角.

图1 双臂机器人简图Fig.1 Double arm robot sketch

双臂机器人的动力学方程通过计算得到如下:

(2)

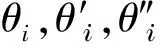
2 模糊逻辑控制器

机器人跟踪轨迹控制的目标是使实际运动轨迹与理论运动轨迹之间误差最小化,定义轨迹跟踪误差为

(3)

式中:θd为理论运动轨迹;θ为实际运动轨迹.

模糊逻辑控制主要有3个组成要素,分别是模糊化、模糊推理引擎(决策逻辑)和去模糊化3个阶段[7].模糊逻辑控制的框图(见图2),第1个块是模糊化,通过查找一个或多个隶属度函数将输入数据的每个元素转换成对应函数的隶属度值.该规则基础和推理基础具有基于模糊概念进行人工决策的能力,以及利用模糊蕴含推断模糊控制的能力及模糊逻辑推理规则的推理能力.模糊集的隶属度函数和模糊控制规则对控制性能有很大影响.第3个操作被称为去模糊化,结果模糊集被模糊化为一个清晰的控制信号.

图2 模糊逻辑控制器结构Fig.2 Fuzzy logic controller structure

在机器人轨迹控制中,模糊逻辑控制的输入变量是转动关节处的误差量e及误差变化趋势e′.模糊控制器的输出变量是联合控制输入量μ.通过模糊化运算,将e和e′映射到语言变量误差量值和数量差异值.模糊逻辑控制的输入是由5种语言术语[8]组成,分别为NB(负方向极大偏差)、NO(负方向中等偏差)、SS(零)、PO(正方向中等偏差)和PB(正方向极大偏差).同时,转动关节的扭矩(模糊控制输出量)被划分为5个相同的模糊集,这组语言术语组成了输入和输出空间的模糊划分.

对于模糊逻辑控制器的输入量和输出量都使用了高斯隶属度函数.高斯隶属函数定义如下[9]:

(4)

式中:c和σ分别为高斯隶属函数的均值和偏移量.

机器人轨迹控制的if-then模糊规则如表1所示,其中规则的总数是25.

表1 模糊逻辑控制规则Tab.1 Fuzzy logic control rules

隶属度函数产生的模糊集必须转换为一个信号,并作为控制输入量发送给控制进程.机器臂的模糊逻辑控制仿真模型如图3所示.

图3 机械臂模糊逻辑控制仿真模型Fig.3 Simulation model of fuzzy logic control for manipulator

3 粒子群算法优化

3.1 粒子群算法

进化计算技术基于群体的运动和智力,寻找最合适的对象点.“群体”是指移动个体的无序集合(群体),其倾向于聚集在一起,而每一个个体都在随机移动.该方法使用了大量的代理(粒子)组成一个在搜索空间中移动的群体以寻找最佳的解决方案.每个粒子都被看作是一个n维空间中的点,其根据自身的“飞行经验”和其他粒子的“飞行经验”来调整它的“飞行”.每个粒子都在问题空间中跟踪它的坐标,这与迄今为止实现的最佳解决方案(适应性)有关,这个值被称为个体最优位置.粒子群优化跟踪的另一个最优值是粒子周围的粒子所获得的最优值,这个值被称为全局最优位置.

粒子群优化算法的概念包括改变每个粒子的速度(或加速度)到其所在的个体最优位置和在每一个时间点上的全局最优位置.每个粒子都根据其当前位置和个体最优位置之间的距离来调整其当前位置、速度,以及当前位置和全局最优位置之间的距离.在每n步中,基于个体最优位置pbest、全局最优位置gbest,第i个粒子的新速度可以表示为[10]

(5)

式中:χ为约束因子;r1,r2为[0,1]之间的随机数;φ1,φ2为学习因子;pbesti为第i个个体最佳位置;gbest为种群中最佳位置;Pi为粒子第i个个体位置.

约束因子为[11]

(6)

通过这种方式改变速度，使第i个粒子搜索它的局部最佳位置pbest和全局最佳位置gbest.根据更新的速度,每个粒子改变的位置为

(7)

3.2 粒子群优化模糊逻辑控制

应用粒子群优化的最关键步骤是选择最佳的成本函数,用于评估每个粒子的适应度.在粒子群优化的寻优过程中,使用3种不同成本函数中的一种作为平方误差(MRSE)的均值、误差的绝对值(MAE)以及基于控制力的参考误差(RBECE).第i个粒子的成本函数如下:

(8)

(9)

|μ1(i)|+|μ2(i)|

(10)

式中:e1(i)为第i样本第1转动关节处的轨迹误差;e2(i)为第i样本第2转动关节处的轨迹误差;N为样本的数量;k为迭代次数;μ1(i)和μ2(i)分别为第1转动关节和第2转动关节处的控制信号.

假设外界干扰因素为正弦波y=sint,设置粒子群算法的种群大小为100,迭代次数为300,学习因子φ1=φ2=2.05,随机数r1=r2=1.通过粒子群优化算法对模糊逻辑控制进行优化的过程块结构如图4所示.所有的模糊逻辑控制参数均在最后时刻(tf)更新,改进模糊逻辑控制成本函数计算结果如表2所示.

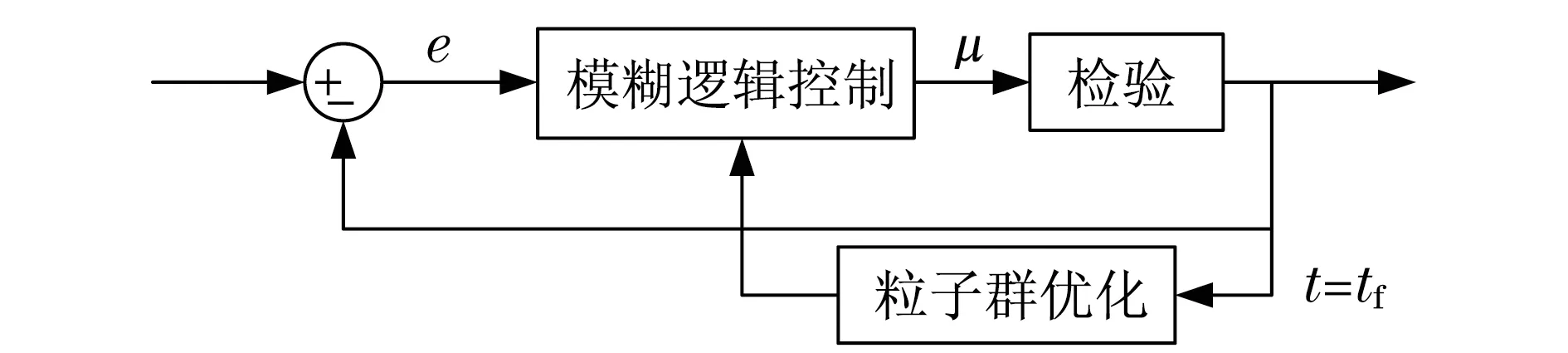
图4 模糊逻辑控制参数的优化过程Fig.4 Optimization process of fuzzy logic control parameters

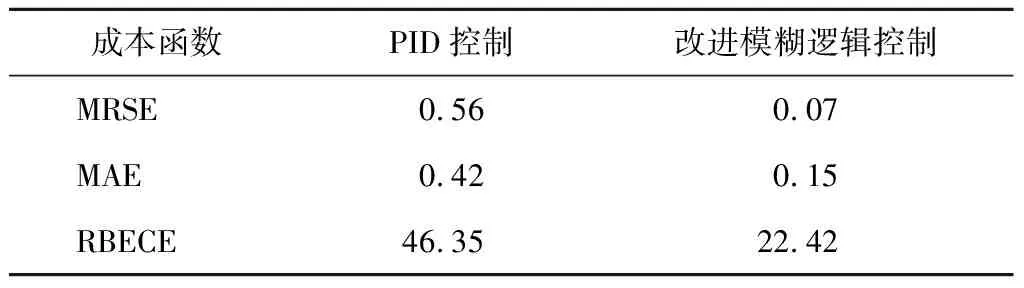
表2 成本函数计算结果Tab.2 The result of cost function calculation

4 仿真结果与分析

为了验证双臂机器人运动轨迹的跟踪效果,采用Matlab软件对机械臂运动轨迹进行数值仿真.仿真参数设置如下:机械臂m1=2 kg,m2=1 kg,机械臂长度l1=1.2 m,l2=0.6 m,g=9.8 m/s2,初始条件为θ(0)= [0 0]T,运动轨迹为θ1=θ2=sin(2t-π/2)rad,外界干扰因素为正弦波y=sint,仿真时间为t=8 s.在无外界干扰情况下,分别采用改进模糊逻辑控制和PID控制对机械臂运动轨迹进行误差仿真,误差曲线如图5所示.分别采用改进模糊逻辑控制和PID控制对机械臂控制力矩进行仿真,力矩波动曲线如图6所示.在正弦波干扰情况下,分别采用改进模糊逻辑控制和PID控制对机械臂运动轨迹进行误差仿真,误差曲线如图7所示.分别采用改进模糊逻辑控制和PID控制对机械臂控制力矩进行仿真,力矩波动曲线如图8所示.

比较图5和图6可知:在无外界干扰情况下,PID控制和改进模糊逻辑控制都能有效地控制机械臂运动轨迹,运动轨迹误差相差不大,同时,采用改进模糊逻辑控制力矩波动相对较小,能够削弱系统的抖动现象.比较图7和图8可知:在外界正弦波干扰情况下,改进模糊逻辑控制明显优于PID控制方法,PID控制机械臂运动轨迹误差较大,在力矩控制方面,采用改进模糊逻辑控制变化不大,控制效果较好.

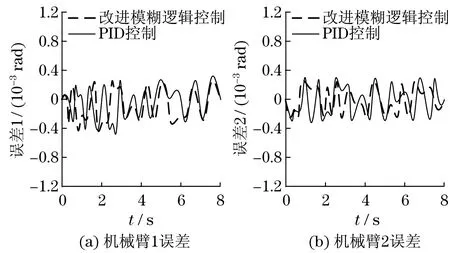
图5 机械臂运动轨迹误差(无干扰)Fig.5 Trajectory error of manipulator (no interference)

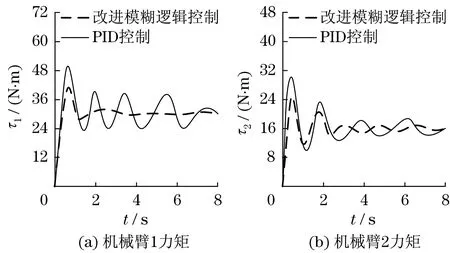
图6 机械臂控制力矩(无干扰)Fig.6 Control torque of manipulator (no interference)

图7 机械臂运动轨迹误差(有干扰)Fig.7 Trajectory error of manipulator (with interference)

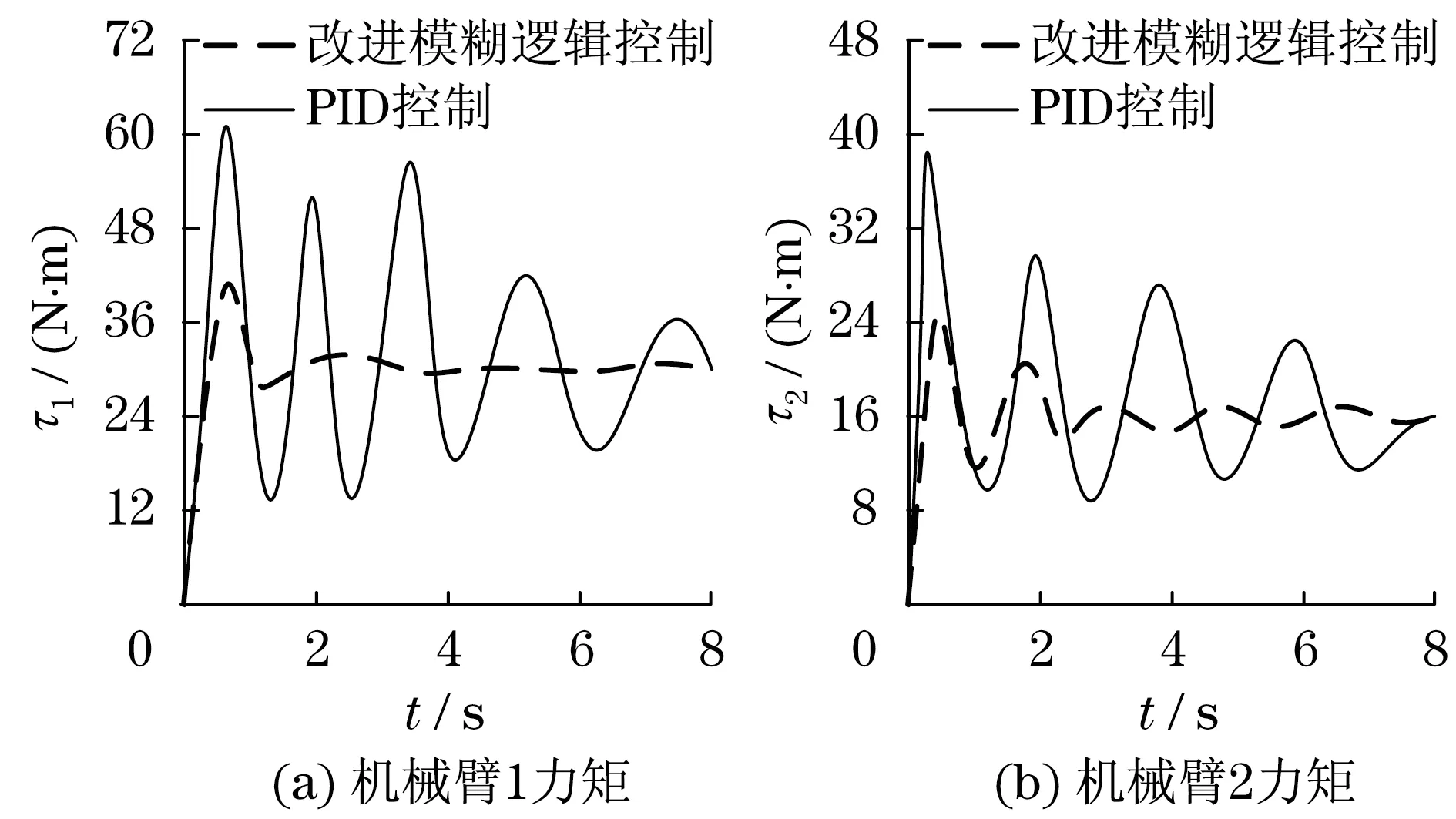
图8 机械臂控制力矩(有干扰)Fig.8 Control torque of manipulator (with interference)

5 结论

针对双臂机器人运动轨迹控制问题,采用了改进模糊逻辑控制方法,并对控制方法进行仿真验证,得到如下主要结论：

(1) 与PID控制方法相比,双臂机器人采用粒子群算法优化模糊逻辑控制后,其平方误差均值、误差绝对值及控制力参考误差值较小.

(2) 在没有外界干扰因素时,改进模糊滑模控制和PID控制都能精确实现双臂机器人运动轨迹的跟踪控制,保证控制系统运动的稳定性.

(3) 在受到外界干扰因素影响时,双臂机器人运动轨迹跟踪精度和抖动幅度采用改进模糊滑模控制方法优于PID控制方法.

参考文献:

[1] 张盼盼.面向复杂自由曲面的喷涂机器人作业规划方法研究与实现[D].南京:东南大学,2016.

ZHANG P P.Research and implementation of planning method for spraying robot based on complex freeform surface[D].Nanjing:Southeast University,2016.

[2] 孙志良.码垛机器人控制系统的设计及实现[D].天津:河北工业大学,2015.

SUN Z L.Design and implementation of control system for palletizing robot[D].Tianjin:Hebei University of Technology,2015.

[3] 王慧东.双关节机器人操作臂控制系统设计[J].自动化技术与应用,2009,28(12):131-133.

WANG H D.Control system design of robot manipulator with dual joints[J].Techniques of Automation and Applications,2009,28(12):131-133.

[4] 付邦晨,王海,邱皖群,等.基于PID的柔性关节机械臂控制策略研究[J].安徽工程大学学报,2016,31(2):45-48.

FU B C,WANG H,QIU W Q,et al.Flexible joint manipulators control strategy based on PID control[J].Journal of Anhui University of Engineering,2016,31(2):45-48.

[5] 赵丹青.机器人的柔性关节机械手控制研究[J].计算机仿真,2011,28(2):244-247.

ZHAO D Q.Research on flexible-joint control for robots[J].Computer Simulation,2011,28(2):244-247.

[6] KUMAR V,RANA K P S.Nonlinear adaptive fractional order fuzzy PID control of a 2-link planar rigid manipulator with payload[J].Journal of the Franklin Institute,2017,354(2):997-1002.

[7] 江一鸣.基于约束优化的双臂机器人协调控制研究[D].广州:广东工业大学,2015.

JIANG Y M.Coordinated control of dual arm robots based on constrained[D].Guangzhou:Guangdong University of Technology,2015.

[8] KUMAR A,KUMAR V.Evolving an interval type-2 fuzzy PID controller for the redundant robotic manipulator[J].Expert Systems with Applications,2017,73(5):163-175.

[9] 夏琳琳,潘旭影,王丹,等.基于类高斯隶属函数的模糊万能逼近器性能分析[J].沈阳工业大学学报,2014,36(3):317-321.

XIA L L,PAN X Y,WANG D,et al.Performance analysis of fuzzy universal approximator based on Gauss-type membership function[J].Journal of Shenyang University of Technology,2014,36(3):317-321.

[10] MUNOZ D M,LLANOS C H,COELHO L,et al.Hardware opposition-based PSO applied to mobile robot controllers[J].Engineering Applications of Artificial Intelligence,2014,28(6):66-75.

[11] MAHMOODABADI M J,TAHERKHORSANDI M,BAGHERI A.Optimal robust sliding mode tracking control of a biped robot based on ingenious multi-objective PSO[J].Neurocomputing,2014,124(2):196-207.