先试后议,让学生经历学习的过程
——“长方形、正方形的面积计算”教学实践与反思
2018-07-05施国柱
□ 施国柱
数学教学必须以学生为中心,让他们自主地经历数学学习的整个过程,体验知识、方法和思想的发生、发展已经成为广大教师的共识,并在实践中进行尝试和探索。那么,教师如何凸显学生的主体地位,让学生经历数学学习的过程?对此,笔者将结合一位新教师的随堂课的数学实践来展开分析思考,内容是人教版三年级下册66页“长方形、正方形面积的计算”。
一、创设和谐氛围,激发探索欲望
【片段一】
师:我们已经学习了长方形的面积,谁能说出黑板的面积有多大吗?
生:大约15平方米吧。
师:黑板比较大,用平方米为单位非常合适。因为结果是估出来的,用上了“大约”,你考虑问题很严谨。
生:我认为大约6平方米,因为上节课学习了1平方米的大小。用1平方米去量,大概6个差不多。
师:用已经学过的1平方米的正方形去量,是一种很好的测量面积大小的方法。你很会学习数学,向你学习(学生自发响起掌声)!用这种方法来估计黑板的面积,会更加接近正确值。黑板很大,操作不方便。我们该怎么来研究它的面积大小呢?
生:它是一个长方形,我们可以先研究纸上的小长方形的面积,找出规律,再计算出黑板的面积。
师:说得太好了!先从小的长方形中探究出面积计算的一般方法,再来计算黑板的面积。下面我们就来研究“长方形的面积计算”。
【反思】
以黑板的面积有多大引入教学,一开始就调动了学生的情绪。因为黑板就在他们的眼前,是一个真实的存在,较好地激起他们探究的欲望。在对话的过程中,教师在倾听的基础上,及时捕捉学生发言中有价值的内容,真诚地予以肯定。学生感受到教师的欣赏,享受着成功的欢乐。同时,教师的评价语也是对全体学生数学地思考问题的引领。
不仅如此,教师还重视数学思想的渗透。“黑板很大,操作不方便,该怎么研究它的面积呢?”学生已经有了这方面的认识基础,自然就想到了需要“变大为小”,“转换”的数学思想得到了悄然渗透。自此,教学内容的进一步展开就显得非常自然。
二、提供尝试机会,展现思维过程
【片段二】
课件显示“例”:一个长方形长5厘米,宽3厘米。你能求出它的面积吗?
师:大家可以用老师发的面积是1平方厘米的小正方形来摆,也可以用其他的方法,求出这个长方形的面积。假如有不止一种的方法那就更好了。
【反思】
这个环节几乎用了5分钟的时间,完全由学生自己拼摆、思考、计算。教师不发声,只是巡视学生的学习情况。
学生在学习新知识前不是一张白纸,他们是带着生活的经验和已有的知识基础走进课堂的。教师抛出需要解决的问题,但不发表个人的意见,这样不会对学生的思维过早地定向引导。从而使学生调动起跟学习内容有关的已有知识和先前经验,努力为解决问题寻求各种可能的路径。在这种状态下,学生的情绪是兴奋的,注意是高度集中的。
郑毓信教授说,努力养成学生“长时间思考”的习惯与能力是我们当前应当特别重视的几个问题之一。而要让学生能够长时间的有效思考,需要具有相当思维含量的问题引领,使他们既有思考的明确目标,又不能轻易地达成。“你能求出长方形的面积吗”引导学生的思维离开了“舒适区”,绞尽脑汁想办法突破现有发展区,向着最近发展区“跳一跳”,再“跳一跳”。此时,教室里的气氛是静谧的,但学生的思维却是异常活跃的。理想的课堂不一定是发言热闹的课堂,而应该是学生用心思索的课堂。
5分钟过后,大多数学生都有了自己解决问题的办法,有的还不止一种。当学生的学习意愿被充分激活,他们的学习力和创造力常常会超出我们的预期。
三、组织精准议论,逐渐形成共识
经过尝试解答后,学生会呈现多种解决问题的方法。并不是所有的方法都要展示,需要组织全体学生共同交流的是能够帮助达成学习目标的内容。通常为三种类型:一是一般的解决问题的方法,二是较为创新的想法,三是存在的典型问题。在学生独立尝试以及之后的小组交流过程中,教师在不停地巡视并与学生互动。其间,除了帮助学生解决存在的个别问题,介入有关小组的研讨外,重要的是寻找有价值的内容,为接下去的全班议论提供载体。
【片段三】
教师选取四种解决问题的方法,逐个展示在投影仪上。

图1

图2

图3
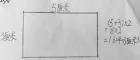
图4
师:请同学说一说是怎么想的?
生1:我用面积1平方厘米的小正方形一个一个铺到长方形里面去,全部铺满后数一数,总共是15个,长方形的面积就是15平方厘米。
师:用面积是1平方厘米的正方形去铺,是一种常用的好方法。总共15个小正方形,你是一个一个数出来的吗?
生1(笑了笑,有些不好意思):5×3,算出来的。
师:能够使用简便方法,很不错。
生2(指着图2):全部铺满太费时间了,只要摆成这样就可以了。第一排摆5个小正方形,说明第二、三排都可以摆5个,不需要再摆了。再看竖的可以摆3个,5×3=15,一共可以摆15个,就是15平方厘米。
师:真有想法!沿着长方形的长可以摆5个小正方形,就是5平方厘米。沿着宽可以摆3个,说明有3个5平方厘米,就是5×3=15(平方厘米)。还有别的想法吗?
生3:也可以这么看,先沿着宽摆,可以摆3个,就是3平方厘米。沿着长摆5个,说明有5个3平方厘米,就是3×5=15(平方厘米)。
师(赞许地点点头):说得真好!
师(指着图3):这位同学是怎么想到这样算的呢?
生4:培训学校里的老师教我的,长方形的面积就是长乘宽。
师:那现在你知道长乘宽为什么就是长方形的面积了吗?
生4:沿着长摆5个正方形,就是5平方厘米。沿着宽摆3个,说明有3个5平方厘米,长方形的面积就是5×3=15(平方厘米)。
师(指着图4):这位同学又是怎么想的呢?
生5(显得有些难为情):我做错了,我把周长和面积混淆了。
【反思】
该片段中,教师的话语不多,但每一句都将学生的思维引向教学的目标,较好地站在了组织者、引导者的位置。“你是一个一个数出来的吗?”这一问题将学生的思维指向了5×3,拉近了达成目标的距离。当生2回答以后,看似教师在复述学生的回答,其实把学生说的“第几排”和“竖的摆”换成了“长”和“宽”,将学生原生态的想法进行了数学化、模型化地归纳,为最终得出长方形面积的计算方法做好铺垫。同时指着图2重点阐述对5×3=15(平方厘米)的意义的理解,使学生看到长方形长是5厘米,每行就可以摆5个1平方厘米,就是5平方厘米;宽是3厘米,就能摆3行。这样,使一维长度数与二维面积单位的个数较好地对应起来。数的意义不同,但大小是相同的,面积单位的总个数就是长、宽两个数的乘积。由此,长方形面积计算公式已经呼之欲出。生4的情况在现在的课堂上是普遍存在的现象,培训学校常常以超前教学来显示它的“成果”。学生在尝试学习阶段虽然能够计算长方形的面积,但不知其所以然。教师让学生复述长乘宽为什么就是长方形的面积,既补上了算理这一课,也是领着全体同学对前面的理解过程的一次巩固。生5的问题是初学长方形面积的三年级学生中普遍存在的,课堂上的提醒有利于学生进一步澄清面积与周长的区别。
在这个议论的过程中,选择的话题要么是对引导学生理解长方形面积公式具有重要支持作用的内容,要么是能够帮助学生理清原来不甚明白或者容易产生混淆的概念。师生间的每一次对话都让全体学生有收获、有感悟,步步深入、层层递进,学生的思维完全沉浸在探究的氛围之中。课堂上没有呈现个别学生恣意表现的快意和学生间热烈争论的场景,但每个学生都那么的专注,他们在享受疑惑被解除以后的喜悦。
由此看来,让学生经历数学学习的过程关键还在于教师如何摆正自己的角色,由对学生不放心、不放手转向充分信任、鼓励尝试。让教学从封闭走向开放,从预设走向生成。教师尽可能地让出话语权,给学生提供自主学习的课堂时空。使他们时时处于主动实践、积极思考的探索状态,让学生的学习真正成为充满思考的学习过程。学生其实很愿意自己去探究,只是有时我们剥夺了他们进行探究的机会。只要我们顺着学生的天性设计和实施教学,课堂上的学习就会真正发生。
