大连黏性土压缩指数与物理指标相关性分析

刘 伽， 朱 斌， 段 磊， 李舒静

(西京学院 陕西省混凝土结构安全与耐久性重点实验室， 陕西 西安 710123)

在土体物理力学指标中，压缩指数是反映土体压缩特性的重要指标。《工程地质手册》中规定，可以采用与变形参数具有相关性、比较容易获取的物理特性指标(如天然含水量、初始孔隙比、干密度、液限与塑限等)，通过经验公式计算得到相应的变形参数，并将此应用于地基沉降计算中。多位学者针对巴西、新加坡、曼谷、日本、韩国等地黏性土进行了系统研究。Skempton等[1～4]建立了压缩指数与液限的经验关系；Koppula[5,6]等认为压缩指数与天然含水率的相关性较好，而Schofield[7～9]等建立了压缩指数与塑性指数的经验模型；魏道垛[10～14]等通过对上海黏土、江苏软土、深圳软土、广州软土的研究，建立了压缩指数与初始孔隙比或天然含水率间的经验公式；Azzouz等[15,16]认为可以采用塑性指数、天然含水率、初始孔隙比、重度、比重等多参数建立与压缩指数的经验关系，并对此进行了深入研究。

土体分布具有典型的地域特征，目前针对大连地区黏性土压缩指数与物理指标相关性的研究相对较少。本文基于大连某人工岛地基岩土勘察资料，通过对黏性土物理力学指标的相关性分析，试图建立压缩指数与物理指标间的经验公式，为该地区地基沉降计算提供参考。

1 大连黏性土指标统计分析

大连某地兴建人工岛工程，勘察结果表明，该地区土体由上至下划分为海相沉积层、海陆交互相沉积层及陆相沉积层。其中，海相沉积层主要由粉质黏土混砂、淤泥质粉质黏土、淤泥及淤泥质黏土组成；海陆交互相沉积层则由黏土与粉质黏土组成；陆相沉积层由黏土与粉质黏土构成。图1为黏性土含水率、孔隙比、比重、干重度、液限、塑性指数及压缩指数随深度分布图，对应数据统计结果见表1。由图可见，含水率随深度增加呈现出先增加后减小的趋势，含水率均值为34.19%。与含水率分布规律相似，孔隙比均值达到了0.96。重度与比重变化范围相对较小，二者均值分别为14.07，2.73 kN/m3。随深度的增加，液限与塑性指数呈先增加后保持稳定的趋势，液限均值为39.00%，塑性指数均值达到了18.76。不同土层的压缩指数变化范围较大，随深度变化呈先增加后减小趋势，均值为0.33。其中，海相沉积层土体的压缩指数较大，为高压缩性土；而海陆交互相沉积层与陆相沉积层则为中或低压缩性土。

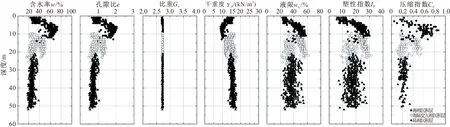
图1 土体指标随深度分布

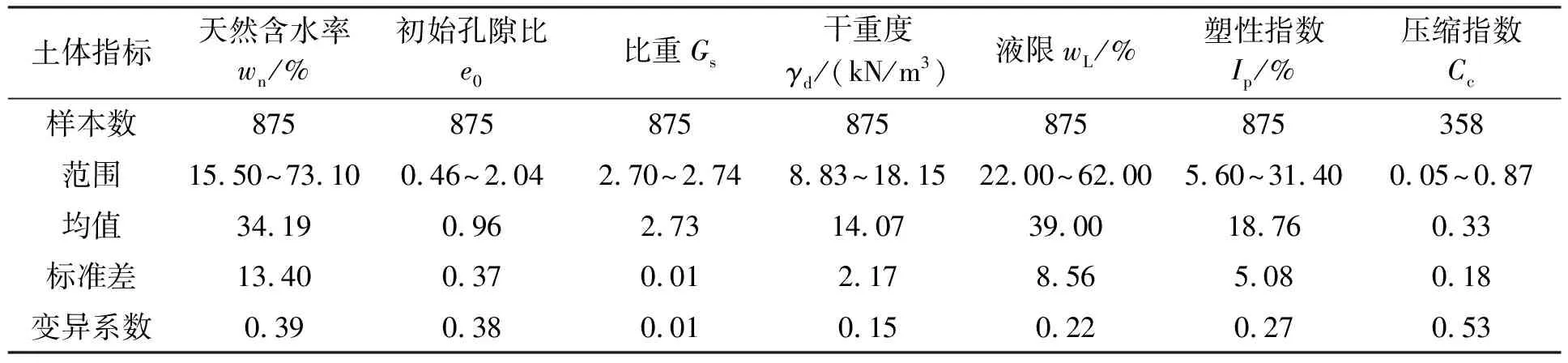
土体指标天然含水率wn/%初始孔隙比e0比重Gs干重度γd/(kN/m3)液限wL/%塑性指数Ip/%压缩指数Cc样本数875875875875875875358范围15.50～73.100.46～2.042.70～2.748.83～18.1522.00～62.005.60～31.400.05～0.87均值34.190.962.7314.0739.0018.760.33标准差13.400.370.012.178.565.080.18变异系数0.390.380.010.150.220.270.53

2 压缩指数与物理指标相关性

2.1 物理力学指标相关性分析

借鉴他人研究成果，与土体压缩指数相关性较大的物理指标为天然含水率、初始孔隙比、干重度、比重、液限及塑性指数。选取上述参数进行相关性分析，结果见表2。由表可见，对于大连黏性土，天然含水率、初始孔隙比、干重度及压缩指数间的相关性较大，相关系数介于0.929～0.999之间。比重与天然含水率的相关性较小，相关系数仅为0.461。对于压缩指数而言，相关性较大的指标为初始孔隙比、天然含水率、干重度；液限与塑性指数次之；比重的相关性最差。鉴于此，本文尝试采用与压缩指数相关性较好的参数(初始孔隙比、天然含水率、干重度)进行单参数回归分析，采用初始孔隙比、天然含水率、干重度、液限及塑性指数等进行多参数回归分析，并将分析结果进行对比。

表2 土体物理力学指标相关性分析(相关系数R)

2.2 单参数回归分析

图2为压缩指数与天然含水率、初始孔隙比及干重度单参数回归分析结果。由图可见，随着天然含水率与初始孔隙比的增加，压缩指数呈增大趋势；而随着干重度的增加，压缩指数呈减小趋势。压缩指数与天然含水率、初始孔隙比及干重度近似为线性关系，相关系数分别为0.942，0.944，0.929。与此同时，选取图2中回归方程与文献中代表性经验公式对压缩指数进行计算，统计压缩指数预测值与实测值比值的均值与标准差，结果见表3。由表可见，当采用液限进行计算时，Terzaghi公式[17]预测结果较好，预测值与实测值比值的均值为0.950，标准差为0.306。当采用天然含水率计算时，Azzouz公式[15]预测结果较好，均值与标准差分别为1.021与0.305，而Yoon模型[4]预测结果偏大。当采用初始孔隙比与塑性指数计算时，Schofield模型[7]预测结果相对较好，均值与标准差分别为0.933与0.308。当采用本文回归方程计算时，压缩指数与天然含水率公式预测结果最好，均值与标准差分别为1.016与0.303，表明预测值与实测值较为接近，数据离散性小，为单参数拟合最优解。

图2 土体压缩指数与物理指标关系

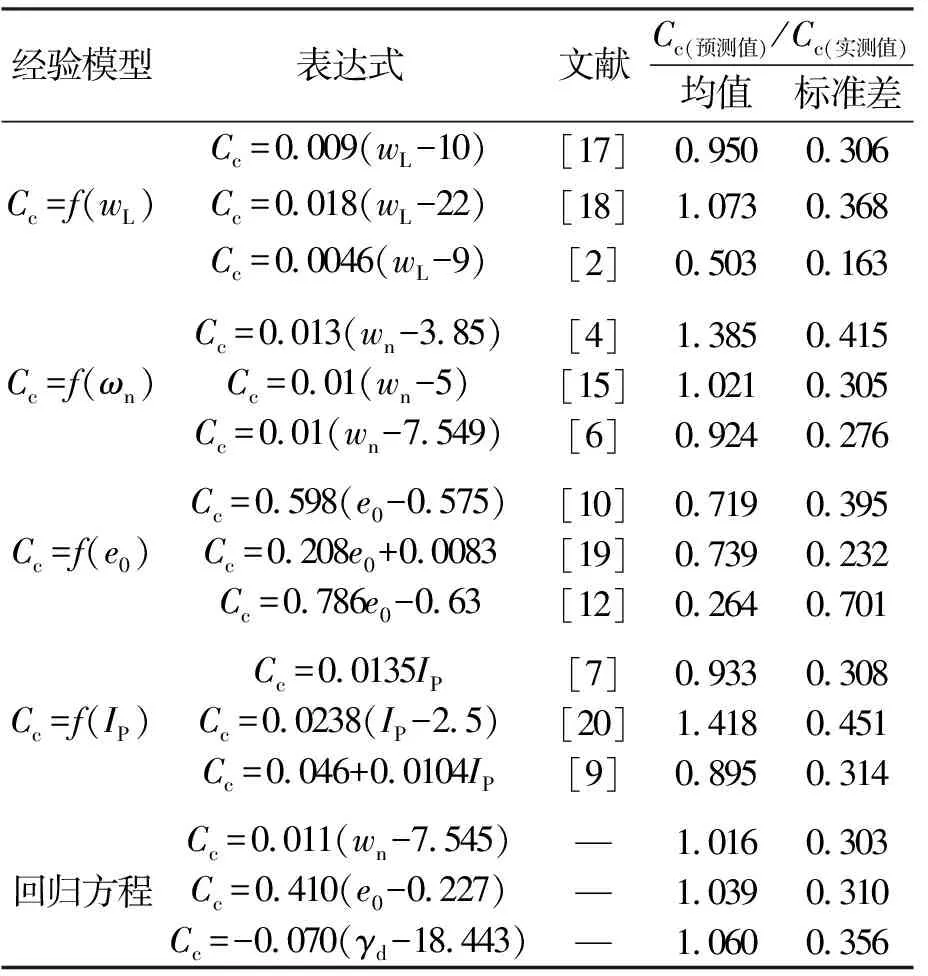
经验模型表达式文献Cc(预测值)/Cc(实测值)均值标准差Cc=f(wL)Cc=0.009(wL-10)[17]0.9500.306Cc=0.018(wL-22)[18]1.0730.368Cc=0.0046(wL-9)[2]0.5030.163Cc=f(ωn)Cc=0.013(wn-3.85)[4]1.3850.415Cc=0.01(wn-5)[15]1.0210.305Cc=0.01(wn-7.549)[6]0.9240.276Cc=f(e0)Cc=0.598(e0-0.575)[10]0.7190.395Cc=0.208e0+0.0083[19]0.7390.232Cc=0.786e0-0.63[12]0.2640.701Cc=f(IP)Cc=0.0135IP[7]0.9330.308Cc=0.0238(IP-2.5)[20]1.4180.451Cc=0.046+0.0104IP[9]0.8950.314回归方程Cc=0.011(wn-7.545)—1.0160.303Cc=0.410(e0-0.227)—1.0390.310Cc=-0.070(γd-18.443)—1.0600.356

2.3 多参数回归分析

表4为采用天然含水率、初始孔隙比、干重度、液限与塑性指数多参数回归分析结果，表中仅列举相关性较好的回归方程。由表可见，5组经验公式相关系数介于0.942～0.960之间。当采用初始孔隙比、干重度、液限组合时，相关性最好，相关系数达到了0.960。当采用干重度、液限、塑性指数组合时，相关系数为0.942。与此同时，采用本文回归方程与文献中代表性的多参数经验公式对压缩指数进行计算，统计压缩指数预测值与实测值比值的均值与标准差，结果见表5。由表可见，采用Azzouz公式[15]预测结果相对较好，预测值与实测值比值的均值与标准差分别为0.955与0.268。采用Yoon公式[4]预测结果低于Azzouz预测结果，均值与标准差分别为0.934与0.324。当采用本文回归方程计算时，预测值与实测值比值的均值介于0.972～1.081之间，标准差介于0.217～0.313之间。其中，采用初始孔隙比、干重度、液限组合时，预测结果最好，均值与标准差分别为0.995与0.217，为多参数拟合最优解。

表4 压缩指数多参数回归分析结果

表5 多参数压缩指数预测值与实测值比值统计结果

注：γw为水的容重

2.4 单参数与多参数预测结果对比

从以上分析可知，当采用单参数经验模型计算时，预测结果最好的为压缩指数与天然含水率经验公式；文献中则为Terzaghi经验模型[17]。当采用多参数经验模型预测时，初始孔隙比、干重度、液限组合时预测结果最好；文献中则为Azzouz模型[15]。图3列出单参数与多参数拟合最优解预测值与实测值分布曲线。由图可见，采用单参数或多参数拟合最优解预测时，数据集中分布于平分线两侧；采用Azzouz公式[15]预测时，数据相对离散，而采用Terzaghi公式预测时，结果严重偏离平分线。从整体预测结果来看，采用本文回归分析得到的多参数组合(初始孔隙比、干重度、液限)预测结果最好、离散性最小。

图3 单参数与多参数拟合结果对比

图4为单参数与多参数拟合最优解频数分布曲线。由图可见，单参数与多参数频数分布曲线均为正态分布。在单参数频数分布曲线中，本文拟合最优解与Terzaghi拟合解[17]分布幅度相差不大，本文拟合最优解峰值更靠近直线(预测值/实测值=1)，而Terzaghi拟合解峰值偏离直线。在多参数频数分布曲线中，本文拟合最优解得到的频数分布曲线更集中、离散性更小。而Azzouz公式[15]得到的频数分布曲线离散性更大，峰值更偏离直线。由此可见，图4频率分布曲线验证了图3分析结论，由回归分析得到的多参数拟合最优解更适用于压缩指数的预测。

图4 单参数与多参数频数分布曲线

3 压缩指数与天然含水率经验模型

在实际计算过程中，多参数在提高预测精度的同时，也使计算过程变的复杂。相反，在预测可靠度允许情况下，采用单参数预测可以简化计算过程。对于单参数而言，天然含水率、初始孔隙比、干重度与压缩指数的相关性较好，且天然含水率更易获取、试验结果的可靠性较高。因此，本文整理了上海、广州、江苏、大连、温州、连云港等地黏性土的试验数据，尝试采用天然含水率对压缩指数进行回归分析，结果见图5。由图可见，压缩指数随含水率的增加而增大，二者近似为线性关系，相关系数达到了0.946。其中，上海、大连、广州地区黏性土拟合结果相对较好，而江苏地区黏性土拟合结果相对较差。对于宁波、温州、杭州等地黏性土，由于试验数据较少，已有数据基本满足相关性。由以上分析可知，对于上海、广州、大连等地黏性土，可以采用本文经验模型由天然含水率来计算压缩指数。然而，土体压缩特性与其物理指标仅仅是一种近似关系，若想得到压缩指数的精确值，必须通过固结试验来获取[21]。

图5 多地区土体压缩指数与天然含水率关系

4 结 论

本文基于大连某人工岛岩土勘察资料，采用单参数或多参数法对压缩指数进行回归分析，建立了适用于该地区压缩指数计算的经验公式。同时，针对上海、广州、江苏、温州、杭州等地黏性土，建立了天然含水率与压缩指数的经验模型。

(1)物理力学指标相关性分析表明，压缩指数与天然含水率、初始孔隙比、重度的相关性较好；与比重的相关性较差。

(2)单参数回归分析结果表明，压缩指数与天然含水率模型预测结果最好，为单参数拟合最优解。多参数回归分析结果表明，采用初始孔隙比、干重度、液限组合时预测结果最好，为多参数拟合最优解。

(3)通过对多地区黏性土压缩指数的回归分析，建立了含水率与压缩指数的经验模型，该模型适用于上海、广州、大连等地黏性土压缩指数的近似计算。

[1] Skempton A W, Jones O T. Notes on the compressibility of clays[J]. Quarterly Journal of the Geological Society, 1944, 100(2): 119-135.

[2] Cozzolino V M. Statistical Forecasting of Compression Index[C]//Proceedings of the 5th International Conference on Soil Mechanics and Foundation Engineering. Paris: International Society for Soil Mechanics and Foundation Engineering, 1961: 51-53.

[3] Tanaka H, Locat J, Shibuya S, et al. Characterization of Singapore, Bangkok, and Ariake clays[J]. Canadian Geotechnical Journal, 2001, 38(2): 378-400.

[4] Yoon G L, Kim B T, Jeon S S. Empirical correlations of compression index for marine clay from regression analysis[J]. Canadian Geotechnical Journal, 2004, 41(6): 1213-1221.

[5] Koppula S D. Statistical estimation of compression index[J]. Geotechnical Testing Journal, 1981, 4(2): 68-73.

[6] Rendon-Herrero O. Universal compression index equation[J]. Journal of Geotechnical & Geoenvironmental Engineering, 1980, 106(11): 1179-1200.

[7] Schofield A, Wroth P. Critical State Soil Mechanics [M]. London: Mcgraw Hill, 1968.

[8] Nacci V A, Wang M C, Demars K R. Engineering Behavior of Calcareous Soils[C]//Proceedings of Civil Engineering in the Oceans III. New York: ASCE 1975: 380-400.

[9] Nakase A, Kamei T, Kusakabe O. Constitute parameters estimated by plasticity index[J]. Journal of Geotechnical Engineering, ASCE, 1988, 114(7): 844-858.

[10] 魏道垛, 胡中雄. 上海浅层地基土的前期固结压力及有关压缩性参数的试验研究[J]. 岩土工程学报, 1980, 2(4): 13-22.

[11] 姜安龙, 郭云英, 高大钊. 润扬大桥南汊北锚碇地基土压缩特性[J]. 建筑科学, 2005, 21(2): 69-71.

[12] 缪林昌, 张军辉, 陈艺南. 江苏海相软土压缩特性试验研究[J]. 岩土工程学报, 2007, 29(11): 1711-1714.

[13] 赵有明, 江辉煌, 张惠明. 深圳地区软粘土变形参数研究[J]. 中国铁道科学, 2004, 25(3): 40-43.

[14] 丁 雷, 江永建, 陈多才, 等. 广州软土的力学特性及相关性分析[J]. 铁道建筑, 2011, (10): 75-77.

[15] Azzouz A S, Krizek R J, Corotis R B. Regression analysis of soil compressibility[J]. Soils and Foundations, 1976, 16(2): 19-29.

[16] Wroth C P, Wood D M. The correlation of index properties with some basic engineering properties of soils[J]. Canadian Geotechnical Journal, 1978, 15(2): 137-145.

[17] Terzaghi K, Peck R B. Soil Mechanics in Engineering Practice[M]. New York: John Wiley and Sons, 1967.

[18] Gao D Z, Wei D D, Hu Z X. Geotechnical Properties of Shanghai Soils and Engineering Applications[C]//Marine Geotechnology and Nearshore/Offshore Structures. Philadelphia: ASTM, 1986: 161-177.

[19] Bowles J E. Physical and Geotechnical Properties of Soils[M]. New York: McGraw-Hill, 1989.

[20] 白 冰, 周 健, 章 光. 饱和软粘土的塑性指数对其压缩变形参数的影响[J]. 水利学报, 2001, (11): 51-55.

[21] 武朝军, 叶冠林, 王建华. 上海浅部土层压缩指数与天然含水率的关系[J]. 岩土力学, 2014, 35(11): 3184-3190.