基于自构建小波神经网络的内模控制

赵彬宏，王建鹏，王元元

(1.山西省自动研究所，太原 030012；2.太原科技大学电子信息工程学院，太原 030024)

内模控制所具有的优良特性使其成为一种便于实际应用的先进控制策略，内模控制系统设计的关键是建立过程的模型及其逆模型。由于非线性过程的复杂性，传统的辨识方法难以获得其精确的模型。神经网络强大的非线性映射能力，可以有效解决非线性系统建模的难题。因此，非线性过程神经网络内模控制方法得到了控制界的关注与发展[1-3]。在诸多类型的神经网络中，小波神经网络(Wavelet neural network, WNN)很好地结合了小波变换的时频局部分析性质和神经网络任意非线性逼近能力。

神经网络的非线性逼近能力和泛化能力均与网络的结构密切相关，许多学者对网络结构的确定进行了研究，并提出一些相关算法[4-6]，文献[7]中为了得到较优的网络结构，提出了一种关于结构的自学习机制，通过隐含层神经元的最大输出值与设定阈值的关系来决定是否产生新的神经元，根据神经元对的作用强度来确定是否需要将其删除。文献[8]中提出了一种自构建RBF神经网络，该网络能够根据给定的判定条件自动增加神经元节点，以满足辨识精度的要求；为了防止网络学习过拟合，基于灵敏度方法对神经网络隐层节点进行修剪删除。文献[9]在文献[8]的基础上，将基于自构建RBF神经网络的内模控制策略应用于舰载火箭炮伺服系统设计中，仿真结果表明了该方法可有效克服非线性因素的影响。此外，文献[10]针对变结构模糊小脑模型进行了研究。神经网络动态变结构的思想，在一定程度上克服了网络结构难以确定的难题，然而，将此类动态网络与内模控制结合的研究还处于起步阶段，仍需要进一步探索。

本文利用自构建小波神经网络建立非线性过程的模型和逆模型，在此基础上设计内模控制系统，使模型辨识网络和内模控制器网络的结构根据系统性能在线调整，采用可以自适应调节步长的梯度下降法优化网络参数，在保证逼近精度的同时提高了网络的收敛速度。仿真结果表明，本文方法可使系统具有跟随输入快、无超调等良好的动态特性，且能在系统受到干扰或过程参数发生摄动时，保持良好的鲁棒性。

1 自构建小波神经网络

1.1 小波神经网络的数学描述

小波神经网络是用小波函数来取代Sigmoid函数的前馈神经网络，且用小波函数的伸缩因子和平移参数分别代替神经网络的权值和阈值。

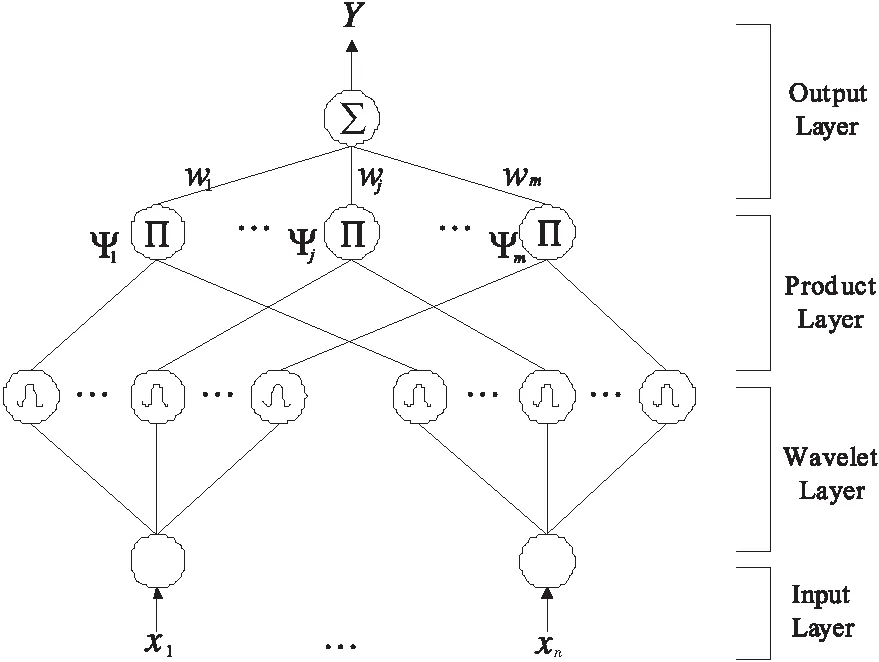
图1 小波神经网络结构图

Fig.1 Structure of the wavelet neural network

图1为n个输入、m个小波基和单输出的小波神经网络结构，小波神经网络共分为四层，分别为输入层、小波层、乘积层以及输出层。小波层节点的激励函数φd,t(x)由墨西哥帽小波母函数Ф(x)变换得出，表达式分别如下：

φ(x)=(1-‖x‖2)exp(-‖x‖2/2)

(1)

(2)

式中,d为伸缩因子，t为平移参数。

若X=[x1,x2,…xn]Т为小波神经网络的输入，那么小波层第j个小波基对第i个输入的激励可表示为：

(3)

乘积层第j个节点的输入为：

(4)

网络的输出为：

(5)

1.2 小波基增加规则

相似性度量用来表示个体间的相似程度，其值越大说明个体间相似度越大、差异越小，与小波基中心距离较近的数据与对应小波基有较高的相似度，且小波基对其激励也较大，据此，可用Dj=|ψj|来表示输入数据与小波基的相似度。把输入样本与小波基的相似度作为空间对象群的属性，根据相似度的变化来实现增加小波基的操作。为了计算方便，把函数取值规范化到(0, 1]，可进行如下计算：Sj=exp[-Dj(xi)]，Sj为关于Dj的单调递减函数，当相似度较大时Sj的取值较小，因此小波基的增加规则如下：

1.3 小波基修剪规则

如果y是系统的实际输出，那么根据神经网络的逼近理论可知，存在一个有着最优结构的理想网络来逼近该输出，设此网络的输出为：

图2 神经网络学习流程图Fig.2 Flowchart of the learning process

(6)

(7)

网络的目标函数取为：

(8)

用泰勒级数展开上式可得：

(9)

(10)

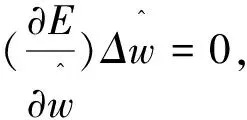
(11)

(12)

式中包含每个小波基对逼近理想输出的作用程度，△E的值较大说明对应的小波基较活跃，且相关参数频繁的更新(修正)，相反，若△E的值较小则对应小波基被认为是不重要的，即该小波基对网络输出的贡献可被忽略。

αj(k+1)=αj(k)×exp{-β×δ[Eth-ΔEm]}

(13)

(14)

αj为第j个小波基对输出的影响程度，其初始值为1.当Eth-△E≥0时，说明第j个小波基对网络没起到有效激励，αj减小，否则其值不变。经过多次无效激励后，若αj≤αth，则第j个小波基可被认为对网络的输出是无效的，可将其删除，αth为预先设定的删除阈值，β为预先设定的衰减率。图2为自构建小波神经网络的学习流程图。

2 自构建小波神经网络内模控制

若过程可逆，则设计神经网络内模控制系统如图3所示，其中，可由自构建小波神经网络逼近过程模型NNM及其逆，即控制器NNC.

图3 神经网络内模控制系统Fig.3 Internal model control system

图中u，y，ym，v，em，yr，e分别为控制量、被控过程输出、模型输出、不可测干扰、模型误差、参考输入以及系统误差。辨识被控过程的模型NNM和逆模型NNC是神经网络内模控制设计的关键，模型的建立可以采取在线或者离线的方式，即分别在在系统运行时，或者利用预先采样的系统输入输出数据建立NNM和NNC，本文采用在线辨识的方式。在建模过程中，NNM的可调参数可根据模型误差em进行训练，同时NNC的可调参数可根据NNM通道反传的梯度信号和系统误差e进行训练。

2.1 过程模型的建立

采用离散时间非线性系统表示非线性过程，即：

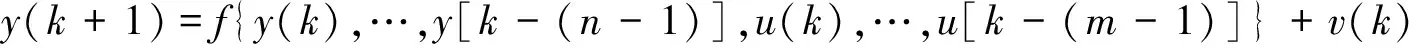
(15)

式中，f(*)为非线性函数，y(k)，u(k)和v(k)分别为过程的输出、输入和扰动，n，m分别为过程输出和输入的滞后时间。

利用小波神经网络建立过程模型，就是利用其强大的非线性映射能力来逼近式(15)中的非线性函数f(*).此时，过程输入和输出的各次滞后可作为网络输入，网络的输出即可表示过程的输出。建立过程模型如下：

输入层：

(16)

小波层：

(17)

乘积层：

(18)

输出层：

(19)

式中，xi(k)为输入层的输入，φd,t(xi(k))为第j个小波基对第i个输入的响应，ψj(k)为第j个小波基的输出，ym(k)为模型的输出，N为输入层神经元个数，M为小波基个数，wj为乘积层与输出层之间的连接权。

神经网络的目标函数如下：

(20)

用梯度下降法调整参数，算法如下：

(21)

(22)

(23)

η为网络的学习步长，选取合适的步长是神经网络收敛的关键，学习率小，收敛速度慢；学习率过大，可能导致振荡。本文采用变步长梯度下降法进行参数的修正，即在参数调整过程中，若误差函数值向小的方向变化，表明误差逐步减小，则学习步长应当增加；相反，若误差函数值向大的方向变化，表明新误差逐步增大，则学习步长应当减小。自适应调节步长的公式如下：

(24)

式中，α、β的取值范围为α≥1，β≤1，本文取α=1.05，β=0.85.

2.2 过程逆模型的建立

根据逆模型的定义，并对yr(k+1)进行线性化预测，则被控过程逆模型的表达式如下：

(25)

此外，还需将em(k)=y(k)-ym(k)反馈到控制器的输入端，所以，神经网络内模控制器的输入输出关系可表示为：

(26)

采用小波神经网络来实现式(26)所表示的非线性函数φ(*).

输入层：

(27)

隐含层：

(28)

乘积层：

(29)

输出层：

(30)

逆模型网络的目标函数为：

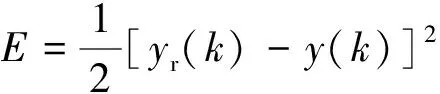
(31)

参数学习算法如下：

(32)

(33)

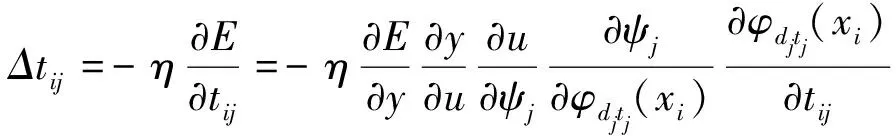
(34)

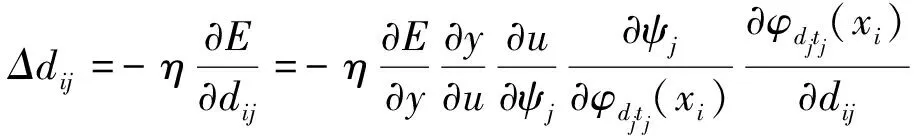
(35)

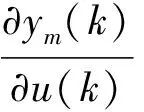
3 仿真及结果分析

为验证本文所提方法的有效性，针对非线性过程进行仿真研究与分析，并与常规神经网络方法进行对比。非线性被控过程如式(36)所示。

(36)

式中，a=1.2，b=1.5.

根据经验公式选取小波神经网络中小波基的个数r：

(37)

式中，p，q分别为神经网络输入和输出的个数，考虑到网络的自构建特性，可取l=0.同时，在基于常规小波神经网络方法中，通过试凑选择l=5.

系统的输入为单位阶跃信号，控制过程中神经网络节点变化如图4所示，可见网络在逼近NNM和NNC的过程中，实现了自构建功能。系统的阶跃响应如图5所示，其中在采样点k=50时系统加入幅值为0.1的输入阶跃扰动，仿真结果表明所提设计方法具有更好的动态跟随和干扰抑制性能。

另外，相同训练次数两种方法的跟踪误差如表1所示，对比可见本文方法的跟踪误差远小于传统方法，表明具有更快的收敛速度。

表1 两种方法的跟踪误差

Tab.1 Tracking errors of two methods

训练次数跟踪误差常规方法本文方法5-1.5焊10-19.0焊10-210-4.3 焊10-22.3焊10-415-1.9焊10-21.3焊10-420-6.2焊10-36.1焊10-5

为了验证控制系统的鲁棒性，在采样点k=50时令过程参数发生摄动，即a=1.0，b=1.3，系统单位阶跃响应如图6所示，可见本文方法具有优于常规方法的鲁棒性。

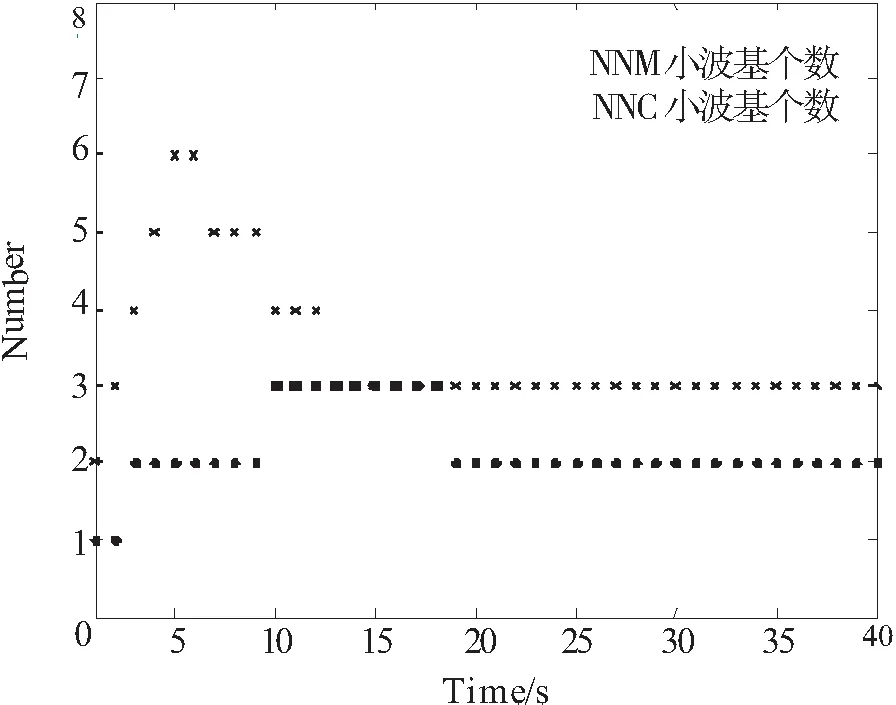
图4 训练过程中小波基的个数

Fig.4 The number of wavelet bases in the training process

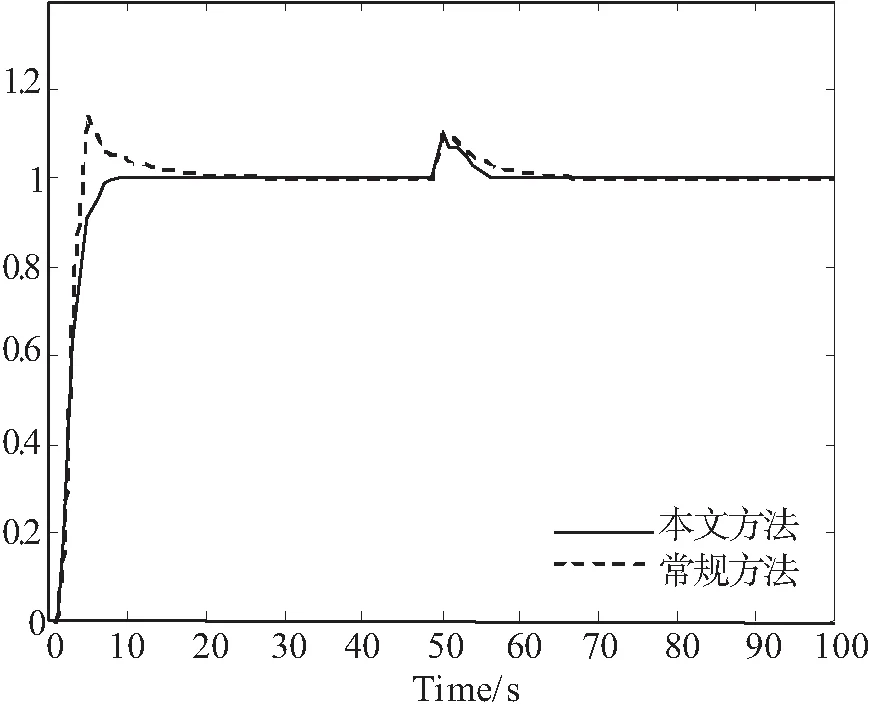
图5 系统的单位阶跃响应

Fig.5 Step response of the system

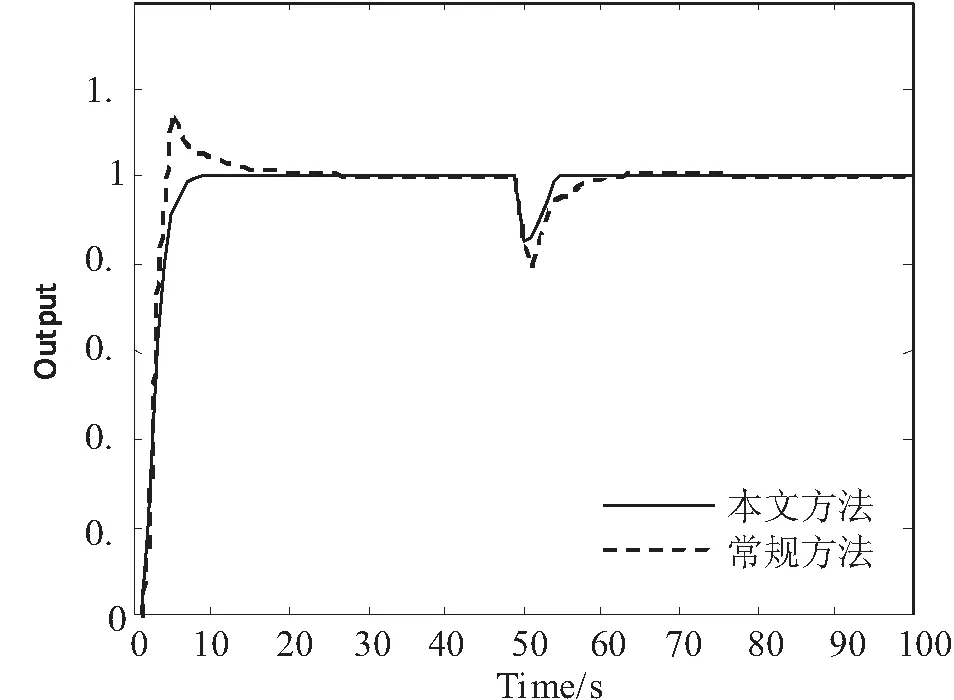
图6 过程参数摄动时系统的阶跃响应

Fig.6 Step response of the system with process parameter perturbation

表2 控制系统的性能指标

Tab.2 Performance indicators of control system

方法标称情况模型失配σ%IAEkσ%IAEk常规14.603.402014.603.6624本文02.87703.015

为了以准确的量化指标验证所提方法的优越性，选择超调量(σ%)、偏差绝对值积分(IAE)以及受扰后恢复稳态的训练次数k作为闭环系统性能指标，指标参数越小意味着系统性能越好。在标称和失配情况下，两种方法的性能指标如表2所示，表明本文方法可使系统具有更好的控制性能。

4 结论

本文提出了一种自构建小波神经网络设计方法，实现了网络结构学习和参数学习，并将该算法与内模控制相结合，针对非线性过程设计了内模控制系统。在控制过程中，如果网络的逼近性能欠佳则增加新小波基以提高其学习能力，如果网络中存在不必要的小波基则删除该小波基以减轻计算负担，参数学习采用可以自适应调节步长的梯度下降法。仿真结果表明，本文方法可使控制系统具有更好的动态性能和克服参数摄动的鲁棒性。

参考文献：

[1] 夏光, 陈无畏, 赵林峰,等. 平衡重式叉车底盘小波网络动态逆内模控制[J]. 机械工程学报, 2015, 51(18): 126-135.

[2] HE Y, ZHENG S, FANG J. Start-up current adaptive control for sensorless high-speed brushless DC motors based on inverse system method and internal mode controller[J]. Chinese Journal of Aeronautics, 2017, 30(1): 358-367.

[3] 张新良, 朱琳, 郭晓迪. 一种频率依赖性迟滞的神经网络内模控制[J]. 测控技术, 2016, 35(9):52-54.

[4] HSU C. Adaptive growing-and-pruning neural network control for a linear piezoelectric ceramic motor [J]. Engineering Applications of Artificial Intelligence, 2008, 21(8): 1153-1163.

[5] LIN C, XU Y. A self-adaptive neural fuzzy network with group-based symbiotic evolution and its prediction applications[J]. Fuzzy Sets and Systems, 2006, 157(8): 1036-1056

[6] HASSEN M, MOHAMED C, NABIL D. Variable structure neural networks for adaptive control of nonlinear systems using the stochastic approximation[J]. Simulation Modelling Practice and Theory, 2006, 14(7): 1000-1009.

[7] CHENG K. Auto-structuring fuzzy neural system for intelligent control[J]. Journal of the Franklin Institute, 2009, 346(3): 267-288.

[8] 赵志诚, 王元元, 刘志远. 一种自构建神经网络的内模控制方法[J]. 控制工程, 2014, 21(1): 111-115.

[9] 曾令梦, 高强, 侯远龙. 基于自构建神经网络的舰载火箭炮内模控制[J]. 火炮发射与控制学报, 2017, 38(4): 40-44.

[10] LEE C, LIN C, CHEN H. A self-constructing fuzzy CMAC model and its applications[J]. Information Sciences, 2007, 177(1): 264-280.