平衡立方体在PMC模型下的1-好邻条件诊断度

赵 昳，原 军

(太原科技大学应用科学学院, 太原 030024)

目前，半导体技术的快速发展使得大规模计算机系统在各领域的应用越来越广泛。然而，要建立一个没有缺陷的大规模计算机系统互连网络是非常困难的。因为在系统中，所有的处理器要同时运行，随着处理器数目的急剧增加，网络发生故障是不可避免的。因此，须及时发现并更换系统中坏掉的处理器，以此来保障计算机系统的可靠性。为此，我们可以用特定的方法，通过系统故障诊断这样一个过程来识别出系统中那些出现故障的处理器。1967年，系统级故障诊断理论是被Preparata等[1]创建的。在研究故障诊断问题的过程中他们利用了图论的方法。在此过程中，Preparata等[1]还提出了第一个该理论所依赖的测试模型——PMC模型。在系统级故障诊断理论中，通过诊断度这一个参数来衡量互连网络系统的故障诊断能力。在一个互连网络系统中，诊断度是该系统能够诊断的最大故障结点机的数目。 经典的诊断度总是不加区分地假定系统的每个结点子集都有可能同时发生故障。这样就会产生一个问题，一般来说，大规模的互连网络系统的一个结点上的所有邻点发生故障的情况少之又少。 从而这样就无法精确地度量大规模互连网络系统的自我故障诊断能力。为了克服以上所述的问题，Lai等[2]对系统中结点的邻点集的故障条件进行约束，要求所有顶点的邻点都不能同时发生故障，由此提出了条件诊断度的概念。类似地， Peng等[3]通过对系统中非故障结点的邻点集的故障条件进行限制，使得每个非故障顶点满足至少有g个非故障邻点的条件，由此提出了g好邻条件诊断度。平衡立方体属于超立方体变形网络，相比超立方体它有更好的性质。本文在前人研究基础上，选取PMC模型对平衡立方体的1-好邻条件诊断度进行了研究。

1 基本概念及符号说明

计算机系统互连网络可以用无向图G=(V,E)来表示，其中图G的顶点集V=V(G)代表网络中的处理器, 边集E=E(G)代表网络中的处理器之间的连接。假设H是V的一个非空子集。顶点集用H表示，则边集即为G中的两端点均在H中的边构成的集合。满足上述条件的顶点集和边集构成的全体的子图，称为H在G中的导出子图，记为G[H]. 一般地，在图G中与顶点v关联的边数，称为顶点v在图G中的度，记为dG(v).特别地，G的顶点的最小度和最大度分别记为δ(G)和Δ(G).若图G中每个顶点的度都是k，称图G为k正则图。给定图G的一个顶点u,N(u)表示在图G中与顶点u相邻的顶点组成的集合。给定取图G的任一顶点集S, 邻集NG(S)是S在G中的与S的顶点相邻的所有顶点的集合。若给定图G的两个顶点u,v, 则C(u,v)表示顶点u,v的公共邻点组成的集合，即C(u,v)={w|w∈N(u),w∈N(v)}. 设F为G的任意顶点子集。G的g好邻条件故障集是指顶点子集F满足条件：V-F中的每一点v在G-F中的邻点个数至少为g, 即V-F中的每一点v的最小度至少为g. 顶点集F称为图G的割若G-F不连通。如果顶点集F既是G的g好邻条件故障集又满足是G的割的定义，则称F是一个g好邻条件故障割。G的g好邻条件连通度是指G中顶点数最少的g好邻条件故障割的阶数，记为κ(g)(G). 其余在本文中没有定义的符号和术语参见文献[4].

采用PMC模型对系统G的两个处理器进行测试时，这两个处理器之间需有物理连线，即这两个处理器要满足相邻的条件。可以用顶点对u,v∈V(G)这种方式来表示系统G中任意一对相邻的结点。其中顶点对左侧的σ(u,v)是测试者，顶点对右侧的u是被测试者。通常用σ(u,v)表示测试结果，σ(u,v)可能是0或1. 假设u没有发生故障。若v是故障的，则σ(u,v)为1;否则，σ(u,v)为0. 反之，假设u是故障处理器，即测试者是故障的，σ(u,v)可能随机的出现0或1, 会得到不可靠的测试结果。所有测试结果的集合σ称为系统G的校验子。校验子σ可以用一个有向图T=(V(G),L)来表示， 其中顶点对(u,v)∈L的充要条件是u和v在图G中相邻。若要故障集F与校验子σ一致需满足下述条件：存在顶点子集F⊆V, 对于任意一条边(u,v)∈L有σ(u,v)=1当且仅当v∈F. 若两个不同的顶点子集F1和F2满足σ(F1)和σ(F2)的交集非空, 则称F1和F2是不可区分的，(F1,F2)是不可区分点对；否则，称F1和F2是可区分的，(F1,F2)是可区分点对。

定义1 若系统G中，故障处理器的个数不超过t，所有的故障处理器通过一次测试全部正确识别出来，就称G是t-可诊断的。在所有使得G是t-可诊断的数中，最大数t称为G的诊断度，记为t(G).

Peng等在文献[3]中对系统中未发生故障的结点的邻集的故障情况加以限制，提出了g好邻条件诊断度的概念。

定义2 设F1和F2是G中任意两个g好邻条件故障集且F1和F2的顶点数至多为t. 若F1,F2是可区分的，则称G是g好邻条件t-可诊断的。图G的g好邻条件诊断度tg(G)是使得G是g好邻条件t-可诊断的t的最大值。

Peng等在文献[3]中提出了G的两个g好邻条件故障集F1和F2可区分的充分必要条件并且研究了超立方体的g好邻条件诊断度。

定理1设F1和F2是G中任意两个相异的g好邻条件故障集， 且|F1|≤t, |F2|≤t. 则G是g好邻条件t-可诊断的当且仅当F1和F2是可区分的。

2012年，Peng等[3]研究了一种较为常见的互连网络——超立方体的g好邻条件诊断度，是在PMC模型的基础上进行研究的。Yuan等[5]在Peng的基础上研究了k元n方体的g好邻条件诊断度。目前，关于一些复杂的互连网络的g好邻条件诊断度的研究成果还较少。

本文研究平衡立方体的1-好邻条件诊断度，下面给出平衡立方体的定义。

定义3 当n≥1时，平衡立方体BHn有22n个点，记为(a0,a1,a2,…,an-1)，其中ai∈{0,1,2,3}，0≤i≤n-1. 每个点与下面2n个点相邻：

(1)(a0±1,a1,a2,…,ai-1,ai,ai+1,…,an-1),

(2)(a0±1,a1,a2,…,ai-1,ai+(-1)a0,ai+1,…,an-1). 其中i是整数且1≤i≤n-1.

定义4 平衡立方体按照递归构造定义如下：

(1)平衡立方体BH1是由四个点构成的圈，四个点分别记为0,1,2,3.

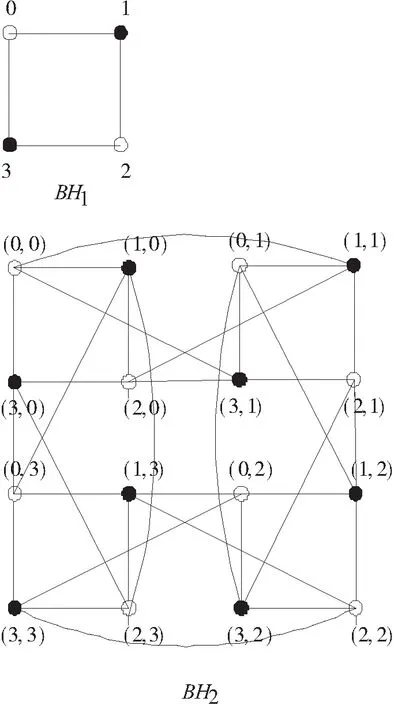
图1 平衡立方体BH1和BH2

Fig.1 Balanced hypercubesBH1andBH2

定理2[6]当n≥2时，平衡立方体BHn的1-好邻条件连通度连通度κ1(BHn)=4n-4.

定理3[7]当n≥1时令u是平衡立方体BHn的任意一点，则存在顶点v, 使得|C(u,v)|=0 或|C(u,v)|=2或 |C(u,v)|=2n，并且有且仅有一个顶点w, 使得|C(u,w)|=2n.

表1表示与顶点(0,0,…,0)距离为2的顶点，以及这些顶点与(0,0,…,0)的公共邻点的个数。

表1 与顶点(0,0,…,0)距离为2的顶点，以及这些顶点与(0,0,…,0)的公共邻点

Tab.1 Vertices with distance 2from vertex(0,0,…,0) and the neighbors vertexes

2 主要结果

先定义顶点集F1,F2以及它们的对称差F1ΔF2=(F1-F2)∪(F2-F1). 下面给出一个由DahBura等在文献[7]中提出充要条件，该充要条件是用来判定PMC模型下F1和F2是否可区分的。

定理4[7]F1和F2是G中任意两个不同可区分的顶点子集当且仅当存在一个顶点u∈V-(F1∪F2),v∈F1ΔF2, 使得边e=uv∈E. 如图2所示。

图2 点集对(F1,F2)在PMC模型下可区分

Fig.2 A distinguishable pair(F1,F2)

引理1 当n≥2时，平衡立方体BHn在PMC模型下的1-好邻条件诊断度t1(BHn)≤4n-1.

证明：在BHn中取a,b,c,d四个点，令a=(0,0,…,0),b=(1,0,…,0),c=(2,0,…,0),d=(3,0,…,0). 令H=(a,b,c,d), 则BHn[H]是一个长度为4的圈。 由定理3和图2可知，N(a)=N(c),N(b)=N(d)且N(a)∩N(b)=∅. 令F1=NBHn(H)，F2=H∪F1, 且BHn-NBHn(H)是不连通的，则|F1|=4n-4, |F2|=4n, 所以|F1|≤4n, |F2|≤4n. 因为H=F1ΔF2,F1=NBHn(H), 由定理4可知F1,F2是不可区分的。

证明F1和F2是1-好邻条件故障集。令Y=V(BHn)-F1∪F2. 因为导出子图BHn[H]是一个长度为4的圈，所以BHn[H]满足最小度至少为1.现在考虑BHn[Y]中的顶点。令u∈Y，由平衡立方体BHn的定义可知，BHn中有且仅有一个顶点满足|N(a)|=|N(c)|=2n，故|N(u)∩F1|<2n. 且平衡立方体是2n正则的。所以，u在Y=V(BHn)-F1∪F2中至少有一个邻点。即BHn[Y]中的顶点满足最小度至少为1.

所以F1和F2是1-好邻条件故障集。

由于F1和F2是不可区分的，|F1|=4n-4, |F2|=4n, 故由定义2和定理1可知当n≥2时，平衡立方体BHn在PMC模型下的1-好邻条件诊断度t1(BHn)≤4n-1.

下面讨论t1(BHn)的下界。

引理2 当n≥2时，平衡立方体BHn在PMC模型下的1-好邻条件诊断度t1(BHn)≥4n-1.

证明：由定义2可知，要证t1(BHn)≥4n-1,只需证明BHn是1-好邻条件(4n-1)-诊断的，也就是要证明在BHn中任意顶点数至多为(4n-1)的两个1-好邻条件故障集F1，F2都是可区分的。

假设BHn中存在这样的两个1-好邻条件故障集F1和F2，它们是不可区分的，并且F1和F2的顶点数不多于(4n-1).由定理4可知，F1和F2不可区分包含以下两种情况：(1)V(BHn)=F1∪F2； (2)V(BHn)≠F1∪F2且V(BHn)-F1∪F2与F1ΔF2之间没有边。不失一般性，假设F2-F1≠∅.

情况1：V(BHn)=F1∪F2.

因为n≥2且BHn的所有点都在F1∪F2中，所以 ：

22n=|V(BHn)|=|F1|+|F2|-|F1∩F2|≤2(4n-1).

矛盾；

情况2：V(BHn)≠F1∪F2,且V(BHn)-F1∪F2与F1ΔF2之间没有边。

因为F2-F1≠∅，F1是1-好邻条件故障集，所以F2-F1中的任意一点在F2-F1的导出子图中至少有一个无故障邻点，即δ(BHn[F2-F1])≥1. 故而|F2-F1|≥2.

断言：F1∩F2是BHn的1-好邻条件故障割。

首先，假设F1⊆F2. 因为F2是1-好邻条件故障集，所以δ(BHn-F2)≥1. 又因为δ(BHn[F2-F1])≥1, 所以F1∩F2是1-好邻条件故障集。由于V(BHn)-F1∪F2与F1ΔF2之间没有边，故V(BHn)-F2与F2-F1不连通。因此，当F1⊆F2时，F1∩F2是BHn的1-好邻条件故障割。

假设F1⊄F2，即F2-F1≠∅，且F1-F2≠∅，因为F1和F2都是1-好邻条件故障集，且V(BHn)-F1∪F2与F1ΔF2之间没有边，所以δ(BHn[F1-F2])≥1,δ(BHn[F2-F1])≥1. 又因为δ(BHn-F1∪F2)≥1, 所以，F1∩F2是BHn的1-好邻条件故障集。由于V(BHn)-F1∪F2与F1ΔF2之间没有边，故V(BHn)-F1-F2与F1ΔF2不连通。因此，当F1⊄F2时，F1∩F2是BHn的1-好邻条件故障割。断言成立。

由定理2可知κ1(BHn)=4n-4. 因为F1∩F2是BHn的1-好邻条件故障割，所以|F1∩F2|≥4n-4. 而|F2|=|F2-F1|+|F1∩F2|, 且|F2-F1|≥2. 因为V(BHn)-F1∪F2与F1ΔF2之间没有边，故N(F2-F1)⊆F1∩F2, 所以有|N(F2-F1)|≤|F1∩F2|.当|F2-F1|=2时，|N(F2-F1)|=4n-2,此时|F1∩F2|≥4n-2. 故|F2|=|F2-F1|+|F1∩F2|=2+4n-2=4n与假设|F2|≤4n-1矛盾。

当|F2-F1|=3时，|N(F2-F1)|≥6n-max{2,2n}=4n,此时|F1∩F2|≥4n. 故|F2|=|F2-F1|+|F1∩F2|=3+

4n与假设|F2|≤4n-1矛盾。

当|F2-F1|≥4时，必有|F2|=|F2-F1|+|F1∩F2|=4+4n-4=4n成立，与假设|F2|≤4n-1矛盾。

证毕。

通过引理1和引理2分别讨论了当n≥2时，平衡立方体BHn在PMC模型下的1-好邻条件诊断度有的上、下界。 综上，有：

定理1 当n≥2时，平衡立方体BHn在PMC模型下的1-好邻条件诊断度t1(BHn)=4n-1.

参考文献：

[1] PRETARATA F P, METZE G, CHIEN R T. On the connection assignment problem of diagnosis systems[J].IEEE Transactions on Computers, 1967, 16: 848-854.

[2] LAI P L, TAN J J M, CHANG C P, et al. Conditional diagnosability measure s for large multiprocessor systems[J]. IEEE Transactions on Computers, 2005, 54: 165-175.

[3] PENG S L, LIN C K, TAN J J M, et al. The g-good-neighbor conditional diagnosability of hypercube under PMC model[J]. Applied Mathematics and Computation, 2012, 218: 10406 -10412.

[4] BONDY J A, MURTY U S R. Graph Theory with Applications[M]. New York: The Macmillan Press Ltd, 1976.

[5] YUAN J, LIU A X, MA X, et al. The g-good-neighbor conditional diagnosability ofk-aryn-cubes under the PMC model and MM* model[J]. IEEE Transactions on Parallel and Distributed Systems, 2015, 26:1165-1177.

[6] YANG M C. Super connectivity of balanced hypercube[J]. Applied mathematics and computation. 2012, 219:970-975.

[7] YANG M C, YANG MH. Reliability analysis of balanced hypercubes[C]// Proceeding of computing, communications and applications conference, London,UK,2012, 376-379.

[8] DAHBURA A T, MASSON G M. AnO(n2.5) faulty identification algorithm for diagnosable systems[J]. IEEE Transactions on Computers,1984, 33:486-492.

[9] LATIFI S, HEDGE M, NARAGHI POUR M. Conditional connectivity measures for large multiprocessor systems[J]. IEEE Transactions on Computers, 1994, 43:218-222.

[10] HAKIMI S L, AMIN A T. Characterization of connection assignment diagnosable systems[J]. IEEE Transactions on Computers, 1974, 23:86-88.

[11] 刘秀丽，原军，马雪. 交换超立方体在PMC模型下的g-好邻条件诊断度[J] .太原科技大学学报 ，2014, 35(5):390-394.