混凝土碳化速率系数的多因素模型

黄 国 理

(广东省建工设计顾问有限公司，广东 广州 510075)

0 引言

混凝土的碳化是混凝土最常见的耐久性问题，大气中的CO2通过混凝土的孔隙进入混凝土内部并与混凝土中的碱性物质发生反应，使混凝土碱性下降，导致混凝土中的钢筋钝化膜被破坏，进而引起钢筋锈蚀。碳化速率系数反映了混凝土的抗碳化能力，因此分析混凝土碳化速率系数的影响因素对混凝土耐久性设计具有重要的意义。

近年来，国内外学者对混凝土碳化速率影响因素做了大量的研究，并建立了相应的预测模型。这些预测模型主要从以下几个方面描述影响混凝土碳化速率系数的因素。基于CO2在混凝土中的扩散过程的阿列克谢耶夫模型[1]和Padakis模型[2]；主要考虑水灰比影响的经验模型如：岸谷孝一模型[3]、依田彰彦模型[4]、朱安民模型[5]等。结合环境因素与材料因素的经验模型如：龚洛书模型[6]、Richardson模型[7]、黄士元模型[8]和张海燕模型[9]。考虑混凝土抗压强度的经验模型如：前苏联碳化模型[10]、牛荻涛碳化模型[11]、邸小坛碳化模型[7]、德国Smolczyk模型[4]等。基于CO2扩散理论并考虑环境与材料因素的半理论半经验模型如：张誉模型[12]、刘亚芹模型[13]、CEB Task Group模型[14]等。上述模型虽然考虑的影响因素众多，具有一定的应用范围，但是没有反映材料因素如矿物掺合料种类与掺量对混凝土碳化速率系数的影响规律，缺少基于材料因素如水胶比、粉煤灰、矿粉的混凝土碳化速率系数多因素模型。

鉴于此，本文通过收集的在标准环境下暴露28 d的混凝土加速碳化试验数据，分析了混凝土材料因素如水胶比、粉煤灰掺量、矿粉掺量对混凝土碳化速率系数的影响规律，进而建立了考虑水胶比、粉煤灰掺量、矿粉掺量的混凝土碳化速率系数多因素模型，为混凝土抗碳化性能的耐久性分析与设计提供了基础。

1 影响因素分析

为了控制碳化环境因素的影响，本文选用通过GB/T 50082—2009普通混凝土长期性能与耐久性试验方法标准中快速碳化试验方法得到的混凝土碳化速率系数试验数据，其标准环境条件为：温度(20±2)℃，湿度(70±5)%，CO2浓度(20±3)%。基于上述试验条件可获得碳化时间为28 d的混凝土碳化深度试验数据，进而由式(1)求得混凝土碳化速率系数[15]：

(1)

其中，X为混凝土碳化深度，mm；t为混凝土的碳化时间，d；k0为混凝土碳化速率系数，mm/d1/2。由于采用了标准碳化试验条件，所以混凝土碳化速率系数主要受材料参数如水胶比(RW/B)、粉煤灰掺量(RFA)以及矿粉掺量(RSG)的影响，因而混凝土碳化速率系数多因素预测模型可以用函数k0(RW/B,RFA,RSG)表示。

1.1 水胶比的影响

水胶比是影响混凝土孔结构的重要因素，水胶比越大，CO2进入混凝土的速度越快，混凝土碳化速率系数越大。由图1a)所示，基于文献[16][19]的试验数据，可得混凝土碳化速率系数随水胶比呈线性增大趋势，所以可以将水胶比(RW/B)与碳化速率系数(k0)的关系描述为：

(2)

1.2 粉煤灰掺量的影响

在混凝土中掺加粉煤灰后，粉煤灰中的活性物质与水泥反应，使得水泥水化生成的可碳化物质减少，混凝土碳化速率加快。由图1b)可知，基于文献[20][21]的试验数据，随着粉煤灰掺量(RFA)的增大，混凝土碳化速率系数呈线性增大趋势：

(3)

1.3 矿粉掺量的影响

随着矿粉掺量的增加，水泥生成的可碳化物质减少，从而使碳化速率系数增大。由图1c)可知，基于文献[22]的试验数据，随着矿粉掺量的增加，混凝土碳化速率系数呈线性增长趋势，由此可以将矿粉掺量(RSG)对碳化速率系数(k0)的影响描述为：

(4)

2 碳化速率系数的多因素模型

根据上文的分析，综合考虑水胶比(RW/C)、粉煤灰掺量(RFA)和矿粉掺量(RSG)的影响，结合式(2)～式(4)，可以建立混凝土碳化速率系数的多因素预测模型：

(5)

其中，k0为混凝土碳化速率系数的预测值,mm/d1/2；α=[α1,α2,…,α6]T为拟合参数。将式(5)展开，并将拟合参数α合并可得：

(6)

其中，b=[b1,b2,…,b7]T为拟合参数。由式(6)可知，复掺粉煤灰矿粉混凝土的碳化速率系数模型包含7个拟合参数，由于并非所有的展开项都对预测模型的计算精度具有显著影响，因此可以采用逐步回归分析法[23]剔除式(6)中的不显著项，从而将式(6)简化为：

(7)

其中，k=[k1,k2,k3,k4]T为拟合参数。基于相关文献[16]～[22],[24]～[31]中的试验数据，可以确定拟合参数k。混凝土碳化速率系数的多因素计算模型如式(8)所示。

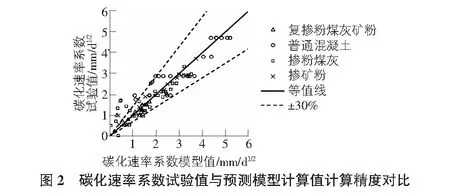
混凝土碳化速率系数模型值与碳化速率系数试验值的对比如图2所示。图2中横坐标为根据式(8)计算的碳化速率系数计算值，纵坐标为碳化速率系数试验数据；图上数据点与等值线越接近，表示模型计算结果越精确。由图2可知，图上数据点基本分布在30%的误差线内，说明所建立的碳化速率系数多因素模型具有不错的精度，且能较好的反映混凝土碳化速率系数与水胶比、粉煤灰掺量、矿粉掺量之间的关系。

(8)

3 模型的对比分析与验证

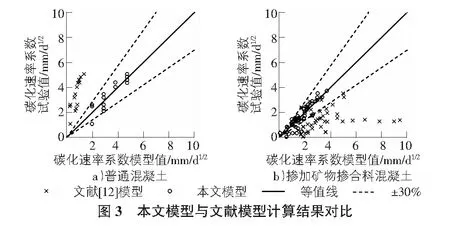
由上节得到的混凝土碳化速率系数模型式(8)，与文献[12]中提出半理论半经验模型进行对比分析与验证，选用相关文献[17][18][22][25][27]～[29][32][33]中的试验数据，对比结果如表1,图3所示。由表1可得，本文模型的残差均方差均较小，且相关系数均较大，说明本文模型具有较高的计算精度和良好的适用性。由图3a)可得，对于普通混凝土，文献[12]模型的计算结果偏低；由图3b)可得，当添加矿物掺合料时，文献[12]模型的计算结果偏高，原因在于矿物掺合料混凝土的水灰比偏大，且没有考虑矿物掺合料种类和掺量的影响，因此计算误差较大。

表1 本文模型与文献模型计算精度对比

4 结语

1)基于混凝土快速碳化试验数据，分析了水胶比、粉煤灰掺量、矿粉掺量对混凝土碳化速率系数的影响。结果表明，混凝土碳化系数模型与水胶比、粉煤灰掺量、矿粉掺量均为近似为线性增长关系。

2)通过逐步回归方法，建立了综合考虑水胶比和矿物掺合料掺量的普通混凝土、掺加粉煤灰混凝土、掺加矿粉混凝土以及复掺粉煤灰矿粉混凝土的碳化速率系数多因素计算模型。

3)通过其他文献模型与试验数据的对比分析，验证了本文模型的有效性和适用性，为混凝土抗碳化性能的耐久性设计提供了基础。

参考文献:

[1] 阿列克谢耶夫.钢筋混凝土结构中钢筋腐蚀与保护[M].黄可信,吴兴祖,译.北京:中国建筑工业出版社,1983.

[2] PAPADAKIS V G,VAYENAS C G,FARDIS M N.Fundamental modeling and experimental investigation of concrete carbonation[J].Aci Materials Journal,1991,88(4):363-373.

[3] 岸谷孝一.铁筋混凝土的耐久性[M].日本:鹿岛建设技术研究所出版部,1963.

[4] 陈树亮.混凝土碳化机理、影响因素及预测模型[J].华北水利水电学院学报,2010,31(3):35-39.

[5] 朱安民.混凝土碳化与钢筋混凝土耐久性[J].混凝土,1992(6):18-22.

[6] 龚洛书,苏曼青,王洪琳.混凝土多系数碳化方程及其应用[J].混凝土,1985(6):12-18.

[7] 曹明莉,丁言兵,郑进炫,等.混凝土碳化机理及预测模型研究进展[J].混凝土,2012(9):35-38.

[8] 许丽萍,黄士元.预测混凝土中碳化深度的数学模型[J].上海建材学院学报,1991,4(4):347-357.

[9] 张海燕,把多铎,王正中.混凝土碳化深度的预测模型[J].武汉大学学报(工学版),2006,39(5):42-45.

[10] 吴建华,张亚梅,孙 伟.混凝土碳化模型和试验方法综述及建议[J].混凝土与水泥制品,2008(6):1-7.

[11] 牛荻涛.混凝土结构耐久性与寿命预测[M].北京：科学出版社,2003.

[12] 张 誉,蒋利学.基于碳化机理的混凝土碳化深度实用数学模型[J].工业建筑,1998,28(1):16-19.

[13] 刘亚芹.混凝土碳化引起的钢筋锈蚀实用计算模式[D].上海：同济大学,1997.

[14] LINDVALL A.Duracrete-probabilistic performance based durability design of concrete structures[A].2nd Int.PhD.Symposium in civil engineering[C].1998.

[15] 牛荻涛,陈亦奇,于 澍.混凝土结构的碳化模式与碳化寿命分析[J].西安建筑科技大学学报,1995,27(4):365-369.

[16] 张亚梅,明 静.3%与20%CO2体积分数下混凝土加速碳化试验研究[J].建筑材料学报,2012,15(5):684-689.

[17] 张海燕.混凝土碳化深度的试验研究及其数学模型建立[D].西安：西北农林科技大学,2006.

[18] 杨 帆.低水泥用量混凝土力学及耐久性能试验研究[D].长沙：中南大学,2008.

[19] 谢东升.高性能混凝土碳化特性及相关性能的研究[D].南京：河海大学,2005.

[20] 陈立亭.混凝土碳化模型及其参数研究[D].西安:西安建筑科技大学,2007.

[21] 都少聪.混凝土连续无损碳化试验研究及碳化综合评价[D].大连:大连理工大学,2012.

[22] 周万良,方坤河,詹炳根.掺粉煤灰、矿粉混凝土抗碳化性能研究[J].混凝土与水泥制品,2012(12):14-19.

[23] 杨绿峰,杨显峰,余 波,等.基于逐步回归分析的随机响应面法[J].计算力学学报,2013,30(1):88-93.

[24] 杜晋军,金祖权,蒋金洋.粉煤灰混凝土的碳化研究[J].粉煤灰,2005,17(6):9-11.

[25] 王培铭,朱艳芳,计亦奇,等.掺粉煤灰和矿渣粉大流动度混凝土的碳化性能[J].建筑材料学报,2001,4(4):305-310.

[26] 吴克刚,谢友均,丁巍巍,等.粉煤灰混凝土的抗碳化性能[J].腐蚀与防护,2008,29(10):596-598.

[27] 杜应吉,黄春霞.大掺量粉煤灰混凝土碳化深度预测模型探讨[J].长江科学院院报,2011,28(3):68-71.

[28] 张小艳,许建民,杜应吉.大掺量粉煤灰混凝土的抗碳化性能研究[J].人民长江,2010,41(6):74-77.

[29] 宋少民,李红辉,邢 峰.大掺量粉煤灰混凝土抵抗碳化和钢筋锈蚀研究[J].武汉理工大学学报,2008,30(8):38-42.

[30] 黄春霞.大掺量粉煤灰混凝土碳化深度预测模型试验研究[D].西安：西北农林科技大学,2011.

[31] 徐 飞.混凝土抗碳化性能的定量设计及其服役寿命研究[D].南宁：广西大学,2014.

[32] 程云虹,闫 俊,刘 斌,等.粉煤灰混凝土碳化性能试验研究[J].公路,2007(12):160-162.

[33] 阿茹罕.大掺量矿物掺和料混凝土的碳化评价方法及影响因素研究[D].北京：清华大学,2011.