基于ODS方法的转子故障分析

侯兴龙，岳林，纪海明

(南京航空航天大学, 江苏 南京 210016)

0 引言

旋转机械广泛地被应用于石油、冶金、化工、电力以及航空等重要的工程领域中[1]。它是以转子及其回转部件作为工作的主体，大部分情况下转子部件都是处于高速运行状态，一旦发生故障，将造成巨大的经济损失和灾难性的后果。因此保证这些关键设备安全、稳定、长周期、满负荷运行对于提高企业经济和社会效益具有十分重要的意义。

1 算法理论

国内外对于转子系统的ODS方法研究还比较少，主要是Ganeriwala SN和Richardson[2]作了一些研究工作，提出了获得频域ODS的一系列方法，包括自功率谱、互功率谱、传递率以及ODS FRF等，并将其应用于桥梁试验中。结果表明ODS FRF方法比传递率方法有更好的消噪效果。Ganeriwala SN等人为了进一步探究ODS方法在转子故障中的实际应用，将ODS FRF方法应用于转子系统不平衡故障中[3]，在旋转设备故障模拟器上，通过比较平衡状态下获得的ODS数据与7种不平衡故障条件下得到的ODS数据，可以发现当转子系统处于不平衡情况下，其ODS将会发生显著的变化，并引入了SCC和SPD参数用来衡量转子不平衡严重程度。

在旋转机械中通过计算ODS的改变量来衡量结构振动程度。为了计算ODS的改变量，通过在数值上比较结构在无故障状态下的ODS与故障发生时的ODS的变化程度，首先引入两个概念。

基准ODS：转子系统在无故障状态下的ODS值；

故障ODS：转子系统在故障发生时的ODS值。

为了比较结构在无故障时ODS值与发生故障后ODS值的改变量，引入两种关键性的数值比较方法。一种方法被称为振型相关系数SCC(shape correlation coefficient)，另一种被称为振型差异百分比SPD(shape percent difference)。这两种计算方法的值都是一个百分数。SCC测量的是结构上两种工况下的ODS的相关性，而SPD是比较基准ODS与故障ODS的百分比差异。

1.1 ODS FRF

ODS FRF方法是一种可以无需计算其激励力信号，直接由响应信号计算得到。它是在传递率函数获得ODS方法的基础之上，由Mark[4]首先提出的。它是通过一个固定参考点与移动响应测点得到，从而获得结构的ODS值，具体公式如下所示：

(1)

式中：Gyy(ω)为结构上参考点的自功率谱；

Gxy(ω)为结构上响应点与固定参考点的互功率谱；

Fx(ω)为结构上响应点的傅里叶变换。

由式(1)可以看出ODS FRF是由参考点与移动的响应信号的互谱值得到的，所以ODS FRF包含了各响应点与参考点之间正确的相位信息，同时公式中也包含了响应点信号正确的幅值信息。而且更重要的是，ODS FRF在共振频率处会产生明显的峰值，这会使仅由响应点信号得到的ODS方法更容易识别结构的模态振型。

当采集测量点的信号时，需要分多次测量，其工况会发生变化。因此需要对计算结果进行校正，可以对每一次获得的ODS结果乘以一个修正因子SFi，其定义如下所示：

(2)

式中：i为当前测量组；

m为测量总次数；

Gyy为当前测量组参考点的自功率谱。

式中的修正因子可以选择任一频率范围，也可以选择某一特定频率处对所得结果进行修正。同样，为了保证测量结果具有较大的信噪比，必须要选择对振源敏感的参考点，而且在分析频率处要保证具有很好的相干性。

通过公式(1)和公式(2)就可以得到相应的ODS向量值。

1.2 振型相关系数(SCC)

SCC是比较结构上两个复数向量之间的相关性，当SCC用来比较的是两个模态振型，它被称为模态置信准则(MAC)，SCC具体定义公式如下所示：

(3)

式中：ODSB为无故障状态下基准ODS向量；

ODSF为故障状态下ODS向量；

‖‖为幅值的平方；

·为两个ODS向量的点乘。

SCC是正常工况下与故障工况下两个ODS向量点积的归一化结果，它的值在[0,1]之间。当SCC计算结果为1表明两种工况下ODS并没有改变，根据经验SCC值>0.9表示ODS发生较小的变化，而SCC的值<0.9时，ODS有较为明显的改变。

SCC是一种旋转机械上ODS改变的数值表示方法。在转子故障诊断中ODS可以根据实际需求由尽可能多的自由度构成，在诊断某一特定类型故障时，往往需要尽可能多的自由度。所以在不同的机械结构中，传感器的安装位置与方向不同，其获得的ODS值也会有所变化。

但使用SCC参数来衡量两个不同工况下ODS变化是远远不够的，因为它只表示了振型的变化。当结构上振型是线性相关的，但其幅值可能是存在变化的，如果机械上ODS的振型没有发生变化，但是其振动水平变的剧烈时，SCC的值可能都是1，得出的结论可能是没有变化，但是其真正的振动水平已经发生改变，会造成误判。为了能够反映结构上振动水平的变化，引进了振型差异百分比(SPD)。

1.3 振型差异百分比(SPD)

SPD是衡量结构上ODS改变量的一种更好的表示方法，因为它不仅仅反映了振型的改变，也反映了振动的剧烈程度，其计算公式如下所示：

(4)

式中：ODSB为无故障状态下基准ODS向量；

ODSF为故障状态下ODS向量；

||为ODS向量的幅值。

如果|ODSF|<|ODSB|，SPD的值为负数。

SPD表示故障状态下的ODS与基准ODS的百分比差异。它在数值上是百分数的形式，当SPD为0时，表明结构在两种工况下的ODS值并未发生改变，当值为1时，表明结构上ODS发生了100%的改变。

总而言之，当机械处于平稳运行并未发生故障的情况下，其SCC的值接近于1，SPD的值接近于0。而当结构发生故障时，SCC的值会下降接近0，而SPD的值会随着振动水平的变化而增大。

所以在转子系统中，可以通过引入两个关键参数SCC和SPD来量化ODS的改变，将其应用于转子系统不平衡、不对中故障中。引进的SCC和SPD值可以作为探测转子系统早期故障的一个重要参考依据。

2 实验验证

为了研究ODS在转子系统故障诊断中的应用，利用ZT-3转子实验台模拟转子进行不平衡、不对中实验，探究其在故障条件下ODS的变化情况，观察其ODS是否明显改变，提出SCC和SPD两个关键参数作为研究旋转机械早期故障的一种方法。

ZT-3转子模拟系统主要由以下部件组成：ZT-3转子故障模拟实验台、MI-7008数据采集分析系统、光电传感器、加速度传感器等部件[5]。其中故障模拟实验台主要由电机、调速器、轴承以及转子轴等零部件组成。它可以控制转子的转速、转子不平衡程度、轴的弯曲程度、碰摩程度以及轴承座与基座的间隙大小，从而可以有效地模拟转子的多种故障。ZT-3转子故障转子实验台如图1所示。

图1 ZT-3型故障转子实验台

2.1 转子不平衡实验分析

不平衡实验系统转速选择分别为2 500r/min、3 000r/min、3 500r/min、4 000r/min，具体故障类型如下：

工况1：故障1(内侧转子处添加2个0.5g的不平衡质量块)在2 500r/min时的情况；

工况2：故障1在3 000r/min时的情况；

工况3：故障1在3 500r/min时的情况；

工况4：故障1在4 000r/min时的情况；

工况5：故障2(内外两侧转子处各添加2个0.5g的不平衡质量块)在2 500r/min时的情况；

工况6：故障2在3 000r/min时的情况；

工况7：故障2在3 500r/min时的情况；

工况8：故障2在4 000r/min时的情况。

SCC与SPD值如图2所示，每一种情况下都是相同转速下基准ODS与故障发生状况下的ODS值比较。

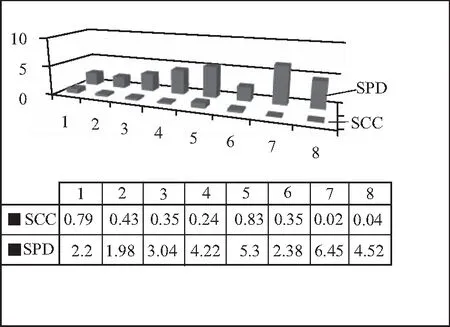
图2 不平衡情况下ODS值比较

图2中，从工况5-8与工况1-4比较中可以看出，在相同转速下故障2的SCC值普遍要低于故障1的情况，而SPD的值可以看出故障2的值要明显高于故障1的值，故障2的振型差异较大，不平衡特性表现得更明显，振动更加剧烈。

2.2 转子不对中实验分析

为了模拟转子不对中状况，实验中在轴承座底部塞入金属垫片，转轴抬高，以至于挠性联轴器联接的轴之间发生不对中故障，垫片的厚度为0.5mm。不对中实验系统转速选择分别为2 500r/min，3 500r/min，4 000r/min，4 500r/min，故障3的垫片厚度为0.5mm,故障4的垫片厚度为0.8mm。

工况1：故障3(外侧转子偏移0.5mm)在2 500r/min时的情况；

工况2：故障3在3 500r/min时的情况；

工况3：故障3在4 000r/min时的情况；

工况4：故障3在4 500r/min时的情况；

工况5：故障4(外侧转子处偏移0.8mm)在2 500r/min时的情况；

工况6：故障4在3 000r/min时的情况；

工况7：故障4在3 500r/min时的情况；

工况8：故障4在4 000r/min时的情况；

不对中状况下的SCC和SPD值如图3所示。每种情况都是在相同转速下，发生故障时获得的ODS值与基准状态下的ODS值对比。

图3 不对中情况下ODS值比较

由图3可知，SCC值在不同工况条件下其结果都>0.9接近1，表明结构在某一转速下基准ODS与故障ODS是线性相关的，但是其SPD在工况1-8时有了较大的改变，表明了故障的发生，在不同工况下其SPD的值都>0，表明了结构ODS的改变；工况1-4与工况5-8相比，在同一转速下，故障4的SPD值要大于故障3的SPD值，说明SPD值可以说明不对中故障的程度，故障4要比故障3严重，而且在同一故障条件下，SPD的值随着转速的升高而增大，振动差异变大，故障更严重。

3 结语

1) 在计算SCC和SPD两个参数中的ODS向量时，选择用ODSFRF的方法，这种方法比一般的传统的其他方法(如传递率法)有更好的信噪比，使测量的ODS向量值更加准确。

2) 当转子系统发生故障时，其结构的ODS发生改变，可以在数值上用SCC和SPD两个关键性的参数作定量描述，SCC表明结构上两个ODS振型是否线性相关，它的值在0～1之间，1表示完全线性相关，发生故障时，其SCC值<1；

3)SPD可以用来衡量两个ODS之间的差异性，因此它是可以定量描述旋转机械的故障程度；

4) 对比不平衡和不对中数据及两幅图可以看出，通过SCC的值可以预测发生了何种故障。当SCC的值接近1时，说明转子一定程度上发生了不对中故障，而相反时，说明转子一定程度发生了不平衡故障。

5) 当故障发生时，SCC减小，SPD随着故障的剧烈程度而增大。在实际应用中，当旋转机械发生故障时，其SPD都会有一个明显的改变，即使ODS变化很小，SPD都会有很明显的表现，因此可以用SCC、SPD来探测旋转机械早期故障及故障严重程度。

[1] 韩捷,石来德. 全矢谱技术及工程应用[M]. 北京:机械工业出版社,2008.

[2] Schwarz B J,Richardson M H. Measurements required for displaying operating deflection shapes[J]. Presented at IMAC XXII January, 2004：26-29.

[3] Ganeriwala S,Schwarz B,Richardson M. Operating deflection shapes detect unbalance in rotating equipment[J]. Sound and Vibration, 2009, 43(1):11-13.

[4] Dossing O. Structural stroboscopy - Measurement of operational deflection shapes[J]. Sound and Vibration, 1988, 22(7):18-26.

[5] 张冰. 滚动轴承的振动特征分析[D]. 南京：南京航空航天大学,2013.