固壁温度对换热系数计算影响的分析研究

周娜，熊元建，戴斌，蔡国煌，苏鹏飞，由旭

(东方汽轮机有限公司，四川 德阳，618000)

1 前言

燃气轮机工作在高温高压环境中，金属部件的温度、应力分布在高温部件中呈现剧烈的变化。优良的流场、温度场和应力场对保证燃机的良好性能和高可靠性十分关键。在燃机强度结构设计工作中，温度、换热系数等参数又为强度、应力、寿命分析提供热边界条件。因此，开展热边界条件分析是燃机设计工作中非常关键的一项工作。

燃机部件如轮盘、中心孔、篦齿气封等的表面换热系数可通过相应的理论公式求得[1-2]。但是理论公式本身所带来的计算误差会影响到热分析所得温度场的准确程度，进而影响到热结构分析的准确性。相比较而言，CFD计算具有其独特的优势，它可以真实地反映研究对象的结构及工作情况，直观地呈现计算结果，减少经验公式所带来的误差。

本文运用CFD工具，同时采用计算流体域和固体壁面热边条的迭代方法，对某型燃气轮机盘腔壁面的换热系数进行计算，得到了壁面的温度和换热系数结果。本工作的主要目的在于尝试手动迭代法得到壁面换热系数的计算方法，检验手动迭代法的可行性，验证固壁温度设置对换热系数计算的影响，为热边界条件的工程应用研究提供一定的指导。

2 迭代计算步骤

手动迭代法，即流体域流动计算和固体域热分析计算分别独立进行，两者之间的温度、换热系数等数据通过手动传输。具体步骤如下：

（1）流体域CFX计算，可得流体域表面的温度Tf，换热系数hf， 热流密度qf；

（2）将CFX计算得到的流体域表面温度Tf和换热系数hf输入固体域Thermal模型中，计算可得固体域表面的温度Ts和热流密度qs；

（3）再将固体域表面的温度Ts输入流体模型中，再次进行CFX计算；

（4）重复步骤（2）和（3）。 理论上， 当流体域表面的热流密度qf和相应固体域表面的热流密度qs相等时，即认为迭代成功。而实际上，两者相等很难实现，因此当迭代所得的表面换热系数值趋于稳定时，即认为迭代计算完成。

3 流体域CFX计算

3.1 物理模型

本文选取了两级轮盘之间的盘腔作为研究对象，目的是求得两级轮盘级间盘腔壁面的热边界条件，即壁面温度和表面换热系数。简化的二维结构如图1所示。流经盘心孔的空气，经过两盘之间的间隙进入盘腔，在盘腔内沿径向外流，经过轮盘端臂上的端面齿间隙和腰形孔到达动叶供气腔。由于端面齿间隙很小，经过它的流量相对腰形孔也很小，本文为了简化计算，只考虑腰形孔。根据该二维结构所建立的流体域物理模型见图2。轮盘端臂全周共有12个腰形孔，可仅取盘腔整周的十二分之一，即30°模型进行计算。

图1 二维结构图

图2 流体域物理模型

为便于流体域和固体域之间壁面数据的传输，将盘腔表面划分成若干个面，各面的位置和命名见图3。

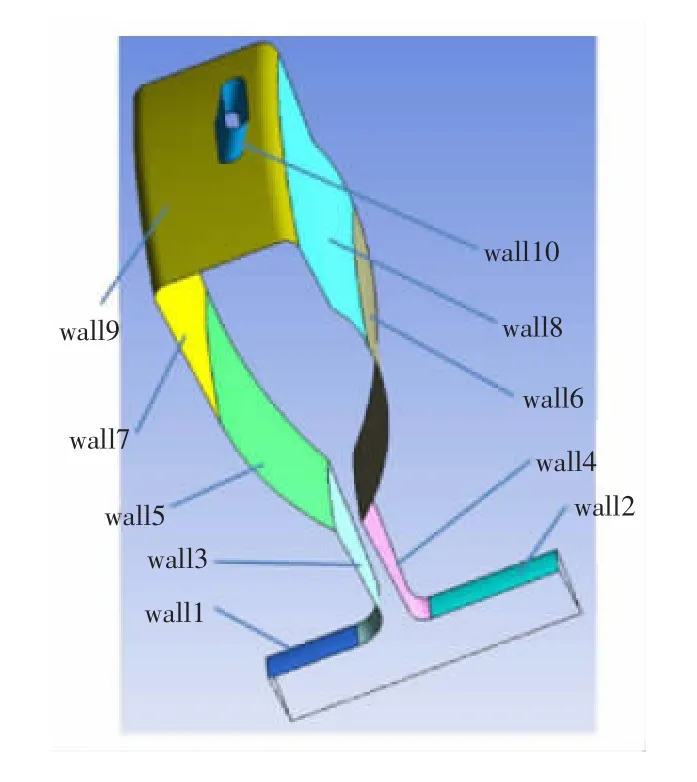
图3 流体域各个壁面的划分及命名

3.2 网格划分

计算模型采用非结构化网格。边界层处网格共15层，第一层厚度为0.01 mm，扩展比为1.2，边界层总厚度为0.72 mm，所得的网格如图4所示。

图4 流体域计算模型网格图

3.3 求解设置

采用SST湍流模型，Heat Transfer选择Total Energy。进口条件为inlet，给定进口总压和总温。出口条件为outlet，给定出口静压。其中各进出口的位置见图2。

4 固体域分析

4.1 物理模型

固体域计算的物理模型见图5。图中同时也给出了wall1、wall2、…、wall10壁面的位置，它们和流体域中wall1～wall10的位置一一对应。

图5 固体域物理模型

4.2 网格划分

固体域的网格划分同流体域的网格划分基本一样，边界层网格的参数设置也相同。

4.3 求解设置

需要输入wall1～wall10各个壁面的流体温度和换热系数来进行求解。这些温度和换热系数来自流体域CFX的计算结果。模型外表面未命名壁面施加第一类边界条件，温度设置为T=900 K。固体域其中一次计算的壁面温度分布如图6所示。

图6 固体域壁面温度分布云图

5 换热系数的修正

流体域对固体壁面表面换热系数h定义如下：

其中：

qf—热流密度， W/m2；

TW—壁面温度，K；

T∞—流体主流温度，K。

本文的迭代计算中，从流体域得到的换热系数hf的定义如下：

其中：

Tf—近壁面第一层网格的流体温度的单元平均值，K。

Tf一般不等于主流温度T∞，因此所得的换热系数hf并非所需的表面换热系数h。需要结合公式（1）和（2），用主流温度对换热系数进行修正，才能得到所需的表面换热系数h。本文主流温度取流体进口温度。

流体换热强烈程度通常用无量纲的Nu数来表征，Nu数表达式为：

其中：

L—计算域的特征长度，m；

λ—导热系数， W/（m·K）。

本文在结果处理中，一般将修正后的表面换热系数h转化为无量纲的Nu数来进行分析。

6 迭代计算A（各壁面假定不同的初始温度值）

对流体域进行计算时，壁面采用第一类边界条件，需给定各壁面温度分布，在初次迭代中对各壁面先分别假定一组初始温度，温度值见表1。

表1 各壁面初始温度值

图7为流体域表面的y+分布云图，壁面所有区域的y+值都在0～30，这是适合于求解换热系数的y+值范围。

图7 流体域表面y+值分布

经过4次迭代计算后，对各个物理量随迭代次数的变化进行了整理，如图8～12所示。

图8、图9分别给出了每次迭代所输入的壁面温度、计算得到的流体域热流密度随迭代次数的变化。其中流体域每次迭代所输入的壁面温度即为上一次迭代中固体域计算所得的壁面温度。可以看出，四次迭代以后，壁面温度和热流密度的值趋于稳定。

图10～12分别给出了每次迭代所得的换热系数hf，根据前述公式修正的表面换热系数h，以及Nu数随迭代次数的变化。观察这些数据发现，各个物理量随迭代次数的变化曲线都比较平缓，尤其是换热系数hf。修正的表面换热系数h和Nu数随迭代次数的变化稍明显一些，但是整体上也比较稳定，特别是第三次迭代以后，各个物理量的值基本不再有明显变化。

比较图8和图10～12发现，壁面温度随迭代次数的变化程度要大于换热系数的变化程度。由于每次迭代的不同之处在于流体域所输入的壁面温度值的差异，也就是说输入差异较大的壁面温度得到了相近的换热系数结果，这意味着壁面温度设置的准确性对我们所关心的表面换热系数影响并不大。

综上所述，经过四次迭代后，所得的表面换热系数结果已基本稳定，我们认为迭代计算工作可以到此结束。实际上，对于大部分壁面来说，经过两到三次迭代已经可以得到相对稳定的换热系数结果。

图8 壁面温度随迭代次数的变化

图9 流体域表面热流密度随迭代次数的变化

图10 流体域表面换热系数hf随迭代次数的变化

图11 修正的表面换热系数h随迭代次数的变化

图12 无量纲Nu数随迭代次数的变化

7 迭代计算B（各壁面假定相同的初始温度值）

前面对wall1～wall10各壁面假定了不同的初始温度进行流体域和固体域迭代计算 （即 “迭代计算A”），发现壁面温度的变化对所关心的表面换热系数影响并不大。为了进一步验证壁面温度对表面换热系数的影响程度，对壁面wall1～wall10全部假定了相同的初始温度，TW=800 K，重新进行了迭代计算，即 “迭代计算B”。计算所用的物理模型以及网格划分设置同 “迭代计算A”完全一样，迭代计算方法也完全一致。

经过两次迭代，得到的各壁面Nu数见图13。图中同时也给出了 “迭代计算A”的Nu数结果以作对比。可以看出，经过两次迭代的“迭代计算B”所得的Nu数跟 “迭代计算A”的结果吻合很好。

根据两种迭代计算的结果，可以得到这样的结论，即：对轮盘壁面温度进行初始设置来获取表面换热系数，在一定温度范围内壁面温度变化对表面换热系数的影响较小。

图13 各壁面无量纲Nu数

8 结论

本文借助CFD工具，应用手动迭代法对某型燃机两级轮盘盘腔壁面的热边界条件进行了计算，得到了壁面温度和换热系数结果。计算结果表明，手动迭代法计算热边界条件是可行的，经过两到三次迭代即可得到比较稳定的换热系数结果；在一定温度范围内，壁面温度对表面换热系数的影响较小，无论是假定不同的壁面温度初始值还是假定相同的壁面温度初始值，都能得到相一致的表面换热系数结果。这样，在工程计算中不用追求准确的壁面初始温度便可得到合理的换热系数。该结论对计算燃气轮机轮盘表面热边界条件具有重要的工程意义。

[1]曹玉璋．航空发动机传热学[M]．北京：北京航空航天大学出版社，2005．

[2]航空发动机设计手册总编委员会．航空发动机设计手册：第16册[M].北京：航空工业出版社，2001．