基于Matlab GUI受不稳定约束弹簧振子运动的研究
2018-07-03张义灵梁冬梅罗志荣玉林师范学院物理科学与工程技术学院广西玉林537000
张义灵, 李 洁, 梁冬梅, 罗志荣(玉林师范学院 物理科学与工程技术学院, 广西 玉林 537000)
0 引 言
在水平面上受稳定约束(即弹簧一端固定不动)的自由振动弹簧振子模型,是由一个实心小球和一轻质弹簧构成,是力学中不可积系统的重要模型[1-2]。文献[3]中对不同控制参数和初始摆角的弹簧摆运动进行了研究,表明当控制参数频率比改变时,弹簧摆的运动较为复杂。文献[4]中对悬挂点在水平方向作匀速或匀变速直线运动的弹簧摆(即受不稳定约束弹簧摆)运动进行了分析和研究,结果表明受不稳定约束弹簧摆的运动比受稳定约束时的运动更为复杂。文献[5]中从不同条件下单摆的自由振动进行数值模拟,发现在大角度摆动时,该系统作非线性运动。文献[6-7]中均是研究在水平面上受稳定约束的弹簧振子运动模型,发现当初速度较小时,弹簧振子在水平面上的运动是准周期运动。文献[8-10]中的研究主要集中在2个或2个以上的弹簧振子系统的运动,都表明了其振动的复杂性。
上述文献主要从不同角度研究了弹簧摆及弹簧振子的运动,但是对于水平面上受不稳定约束(即弹簧一端可以移动)的弹簧振子运动的研究尚未见报道。鉴于此,本文运用Matlab GUI[11-16]对在水平面上受不稳定约束的弹簧振子的运动进行研究,通过设计GUI进行数值模拟,作出系统的演化曲线、相图以及运动轨迹,直观地研究弹簧振子的运动规律。
1 系统的动力学方程
如图1所示,在水平面上受不稳定约束的弹簧振子模型,是由一个轻质弹簧和一个大密度的实心小球构成,其中弹簧的劲度系数为k,原长为l;球的质量为m,直径忽略不计,视为质点。在水平面上建立直角坐标系,分别令弹簧自由伸长点为弹性势能零点,质点小球所在的水平面为零重力势能面,质点小球的坐标为(x,y)。弹簧与x轴的夹角为θ0,其一端与x轴交于点A,另一端连接小球。在时间t=0时刻静止释放小球(初速度为0),同时使点A以速度v开始沿x轴无摩擦向右作匀速直线运动,求弹簧振子的运动情况。

图1 水平面上受不稳定约束的弹簧振子示意图
该系统为保守系统,其拉格朗日方程可以表述为[1,7]
(1)
系统的动能T和势能V分别为:
系统的拉格朗日函数为
(4)
将式(4)代入式(1),其中q1=x,q2=y,则系统在直角坐标系中的动力学方程为:
(5)
2 系统动力学方程的求解
为方便数值计算,对式(5)进行降阶处理。定义4个列向量矩阵y=[y1y2y3y4],设y1=x,y2=dx/dt,y3=y,y4= dy/dt,化为一阶微分方程组:
(6)
本文运用Matlab中ode 45指令求解非刚性的常微分方程(ODE)式(6),求解语句如下:
[t,y]=ode45('zysfun',[0:0.01:str2num(get(handles.tfinal,'string'))],y0,[],k,m,l,v)
其中:zysfun为系统的子函数文件名,步长为0.01,tfinal为模拟时间结束点;y0为初始条件矢量,k,m,l,v为运动参数。
根据式(6),将系统的微分方程表示为odefun函数的编写形式,其程序语句如下:
functionydot=zysfun(t,y,flag,k,m,l,v)
ydot=[y(2);-k/m*(y(1)-v*t)*(1-l/sqrt((y(1)-v*t)^2+y(3)^2));y(4); -k/m*y(3)*(1-l/sqrt((y(1)-v*t)^2+
y(3)^2));]
并保存为zysfun.m文件。在t=0 s时,小球初速度为零,矩阵y的初值y0= [y10y30],其中y1、y3为小球x方向、y方向上的初始位置。
3 系统GUI设计思想
图2为在水平面上受不稳定约束弹簧振子的GUI初始界面设计。

图2 GUI初始界面设计
运用可视化界面探究该系统,具体操作步骤如下:① 对系统进行分析,静止释放小球,同时点A沿x轴作匀速直线运动,运用拉格朗日方程建立直角坐标系下的动力学方程;② 根据第①步的分析,完成设置控制区域的编辑框、静态文本框以及对Push Button按钮编写Callback(回调函数);③ 在已知运动参数以及模拟时间的情况下,运行GUI,通过点击“计算”按钮,激活其他按钮;点击“曲线”按钮,弹簧振子的运动情况以曲线形式展现;点击“保存数据”按钮,计算结果输出并保存在Excel文件;④ 最后通过给定的初始条件,输入不同的运动参数,观察分析得出不同情况下弹簧振子运动的结果。
4 仿真系统演示界面
在简谐振动的运动学普遍定义中,质点运动的动力学方程式为[1]
(7)
式中,频率ω0=k/m。由式(5)和(7)可知,ω0取决于弹簧的劲度系数k和小球质量m。在k和m的值一定时,研究弹簧振子在不同初始条件下的运动情况。
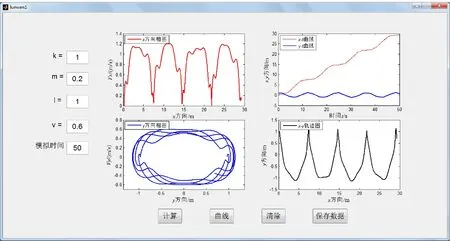
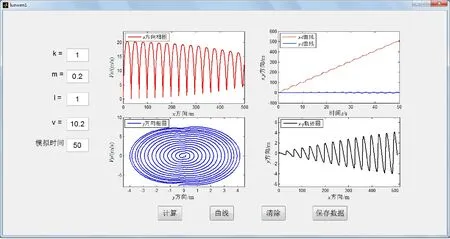
在该系统体系下,选取k=1 N/m,m=0.2 kg,l=1 m,模拟时间取50 s,步长为0.01,当初始角度较小(θ0=5°)和较大(θ0=75°)时,初始条件分别为y0=[0.996 0 0.087 0]和[0.259 0 0.966 0]。当速度分别取较小(v=0.6 m/s)和较大(v=10.2 m/s)值时,弹簧振子运动的情况如图3和图4所示。

(a) θ0=5°
(b) θ0=75°
在图3 (a)中,当速度(v=0.6 m/s)和初始角度(θ0=5°)都较小时,由x方向相图、x-t曲线可见,弹簧振子在沿x方向上作准周期运动,振幅随横坐标时间t作周期性变化的振动,与“拍”现象相似,其特征为:图中上、下两部分的峰不对称,其中上半部分的峰宽度大,而下半部分的峰较尖锐;从y方向相图、y-t曲线可知,弹簧振子在y方向也作准周期运动,同时可以看到一个有趣的现象,以坐标(0.087,0)为起点,在0~1.307 1 m之间,先向右作半径逐渐增大的螺旋式运动到右端点,然后再向左作半径逐渐减小的螺旋式运动回到起点附近坐标(0.047,0.013 4)处,这样一个螺旋式来回准周期运动;从x-y轨迹图可知,弹簧振子在二维空间作类似于正弦图像的准周期运动。而当初始角度较大(θ0=75°)时,通过观察图3(b)可知,x方向相图无明显特征;在x-t和y-t曲线上的幅度波动较大,得到的运动轨迹无规则变化,弹簧振子在二维空间不再作准周期性运动。但观察y方向相图可知,弹簧振子在y方向仍作准周期运动。
(a) θ0=5°

(b) θ0=75°
图4为速度较大(v=10.2 m/s)时的模拟图,通过观察图4(a),当θ0=5°时,由x方向相图、x-t曲线可知,弹簧振子在x方向上仍作准周期运动,但相对于“拍”现象不太明显,其特征与v、θ0较小时相类似;由y方向相图、y-t曲线可知,弹簧振子在沿y方向作类似于“旋涡”运动,其运动形式为以小中心口为起点,而后半径逐渐增大;但观察x-y运动轨迹图可得,弹簧振子在二维空间作准周期性运动,其特征变化与“拍”现象相似。当θ0=75°时,通过观察图4 (b)可知,弹簧振子在二维空间仍作准周期性运动,其中在x方向相图与x-y轨迹图上,“拍”现象明显,而在y方向相图上,其运动结构则是复杂的闭合曲线,作准周期运动。
由图3和图4的分析可得,在θ0、v较小时,弹簧振子在二维空间作类似于正弦的准周期性运动,而在v较小,θ0较大时,弹簧振子将不再作准周期性运动;在v较大时,弹簧振子的运动情况受初始角度θ0的影响较小,仍然在二维空间作单一的半径增大螺旋式准周期运动;通过比较分析图3(a)和4(a)可知,在θ0较小时,弹簧振子的运动受速度影响较小,均作准周期运动;比较图3(b)和4(b)可得:在θ0较大时,弹簧振子的运动受速度影响较大。
5 结 语
本文利用拉格朗日方程推导出在水平面上受不稳定约束弹簧振子运动的动力学方程,运用Matlab GUI对弹簧振子运动情况进行仿真。在水平面上弹簧一端作匀速直线运动时弹簧振子的运动情况较为复杂,弹簧振子运动与弹簧一端的速度大小和初始角度有关;在一定条件下,系统在二维空间作准周期运动。由于篇幅的限制以及系统振动的复杂性,本文只考虑了弹簧一端作匀速运动时不同初始角度下的弹簧振子运动情况,但如果考虑在不同初始条件下弹簧一端作匀变速直线运动,那么弹簧振子的运动情况会更加复杂,我们将作下一步的研究。
参考文献(References):
[1] 漆安慎, 杜婵英. 普通物理学教程·力学[M]. 3版. 北京:高等教育出版社, 2012.
[2] 赵凯华, 罗蔚茵. 新概念物理教程·力学[M]. 北京:高等教育出版社, 2001.
[3] 杨正波, 夏清华, 刘思平. 不同控制参数下的弹簧摆[J]. 大学物理, 2011, 30(5):23-26.
[4] 夏清华, 屈少华. 受不稳定约束弹簧摆运动的研究[J]. 大学物理, 2015, 34(4):6-10.
[5] 李 硕, 赵彤帆, 李根全,等. Matlab软件在单摆自由振动中的应用[J]. 实验室研究与探索, 2013, 32(11):65-68.
[6] 李 阳, 王 宏, 韩艳玲. 与r的一次方成正比有心力作用下质点的运动研究[J]. 物理通报, 2015, 34(12):4-8.
[7] 李 阳, 王 宏, 韩艳玲,等. 在水平面上受稳定约束的弹簧振子运动研究[J]. 广西物理, 2015,36(2):31-34.
[8] 黄 焱. 双弹簧振子在竖直方向的自由振动研究[J]. 大学物理, 2014,33(9):20-23.
[9] 何松林, 黄 焱, 戴祖诚. 对称双弹簧振子横向振动的复杂性研究[J]. 昆明学院学报, 2010, 32(3):86-88.
[10] 杨正波, 夏清华, 刘思平. 多弹簧振子耦合系统运动研究[J]. 大学物理, 2010, 29(4):29-32.
[11] 钟可君, 张海林. 基于Matlab GUI设计的光学实验仿真[J]. 实验室研究与探索, 2010, 29(10):52-53.
[12] 朱飞宇, 徐志宇, 黄国辉,等. 基于MatlabGUI的三容水箱液位实时监控系统设计[J]. 实验室研究与探索, 2017,36(9):83-86.
[13] 温 正. MATLAB科学计算[M]. 北京:清华大学出版社, 2017.
[14] 罗华飞. MATLAB GUI设计学习手记[M]. 3版. 北京:北京航空航天大学出版社, 2014.
[15] Hunt B R, Lipsman R L, Rosenberg J M. A guide to MATLAB: for beginners and experienced users[M]. Cambridge: Cambridge University Press, 2014.
[16] Zhang Z, Bai H, Yang G,etal. Computer simulation of Fraunhofer diffraction based on MATLAB[J]. Optik-International Journal for Light and Electron Optics, 2013, 124(20): 4449-4451.
