股市相关结构：动态演化过程与稳定性特征——基于随机矩阵理论与偏相关系数矩阵方法对中国2015年股灾的分析

杨红伟，江 涛，王励励

(1.浙江工商大学 统计与数学学院，浙江 杭州 310018；2.浙江财经大学 中国政府管制研究院， 浙江 杭州 310018；3.浙江工商大学 国际商学院，浙江 杭州 310018)

一、 引 言

股票市场作为一个复杂系统，其内部结构通过股票之间的相关性程度来体现(Plerou 2002)[1]。量化股票之间的相互关系，区分股票市场价格波动的“噪声”和“市场信息”*在经验数据相关系数矩阵中，“噪声”是指符合随机矩阵性质的部分，“市场信息”是指偏离随机矩阵理论值的差异部分。，分析市场相关结构的演变过程和稳定性特征，是构建投资组合与风险管理的重要依据。随着中国经济金融的发展，股票之间的相依性日益增加，从而引发的系统性风险也日趋频繁。迄今为止，中国已经爆发了九次股灾，*股灾是指股市内在矛盾积累到一定程度时，由于受某个偶然因素影响，突然爆发的股价暴跌，从而引起社会经济巨大动荡，并造成巨大损失的异常经济现象(陈华，2015)[2]。每次都给投资者带来巨大损失(陈华，2015)[2]，且股灾容易引发金融危机等灾难性后果(杜军，2016)[3]。

2015年，中国股市经历了罕见的股灾，致使沪深两市市值减少十几万亿，新股停发、直接融资中断，造成了巨大损失(谢百三和童鑫来，2015)[4]。在股灾前、中、后三个阶段，股市相关结构发生了什么变化？在这些变化中哪些部分代表了市场共同行为？股灾期间是否仍存在不变的稳定性因素？这些都是本文研究的主要问题。通过对股灾期间股市相关结构的主要特征变化研究，进一步把握市场微观运行规律，有助于深入理解股灾的发生机制与演变机理，从而可能帮助政府监管部门和投资者对股灾进行预判，对未来金融危机的发生概率进行预测，并对市场风险进行有效监管。

本文将通过对已有股市相关结构文献的梳理，基于随机矩阵理论和偏相关系数矩阵方法研究中国上证A股的高维股票资产相关结构，深入分析2015年股灾前、中、后三个阶段中国股票市场相关结构的动态过程和稳定性特征，并考察1998年以来股市相关结构的长期演变过程，最后通过上述研究提出相应的建议。由于金融高频数据包含了更为丰富的市场信息，因此研究采用的数据为2014年7月至2017年6月(包括股灾前、中、后三个阶段)的5分钟交易收益率，鉴于高频交易数据估计的股市相关系数矩阵，受到市场微观结构噪声的影响会存在估计误差，文中采用60分钟交易数据进行对照分析；*与5分钟交易数据相比，60分钟交易数据的相关系数矩阵估计受市场微观结构影响小，但样本量显著下降，则使其面临“维数灾祸”问题而导致估计结果存在偏差，因此文中对两类高频数据进行比较研究。同时，采用1998年1月至2017年6月的日交易收益率分析股市相关结构的长期演变过程。

二、 文献综述

中国股市发展时间较短，市场机制还不健全。早期研究认为，中国的股票市场弱式有效性并不成立，存在各种统计套利和投机机会(张亦春和周颖刚，2001；陈灯塔和洪永淼，2003；吴振翔和陈敏，2007)[5-7]，也有学者提出1993年以后市场达到了程度非常低的弱式有效性水平(马向前和任若恩，2002)[8]。而随着股市的不断发展，近期成果显示，市场弱式有效性在逐步提高(高蓉等，2012)[9]，在部分时期或有摩擦条件下达到弱式有效(张鹏，2016；屈博和庞金峰，2016)[10-11]。然而在2014-2016年期间，上证交易所中的“散户”(即资金量低于1000万的自然人投资者)持有市值占比均高于专业投资机构*根据《上海证券交易所2015-2017年统计年鉴》，2014-2016年期间散户投资者年平均持有市值占比为16.87%，高于机构投资者的14.90%。其中，2014-2016年散户投资者持有市值占比分别为17.87%、16.5%和16.23%，机构投资者持有市值占比分别为14.65%、14.49%和15.58%。。刘维奇和刘新新(2014)[12]发现，机构投资者在市场上表现得更为理性，他们的情绪能够预测后市，而个人投资者情绪不具有预测性。这意味着中国股市容易受到“市场情绪”的影响，股市价格的波动中很可能存在显著的市场共同行为，即“过度联动”现象*Kallberg和Pasquariello(2008)[13]指出，不能被基本面因素所解释的资产价格间的共变性被称为过度联动(Excess Comovement)。根据Markowitz(1952)[14]的均值-方差最优投资组合理论，股票间相关性越高，投资组合的风险越难以分散。拓展到整个市场，则代表股市“过度联动”现象越显著，风险也越高，从而容易导致股灾的发生。而股灾不同于其他一般的股价波动，具有突发性、破坏性、联动性、不确定性等特征，相比国外股市的股灾，中国股灾具有自身的一些特点，例如周期短、平均振幅大等(陈华，2015)[2]。而2015年的股灾发生时又包括了连续单日大幅度波动、多次千股跌停、大面积上市公司停牌潮等主要特点(谢百三和童鑫来，2015)[4]。

关于股灾期间市场内部相关性上升的现象，马丹等(2016)[15]认为股票市场在危机事件的冲击下会导致板块间的传染效应迅速增加，从而使股票收益相关性处于非常高的水平。一些实证研究证实股灾及影响更为严重的金融危机期间，股市相关性均会显著提升。例如Han等(2017)[16]通过对金融危机前后的2007年与2008年沪深A股的分时数据的分析，得出我国股市在金融危机期间相关性更加显著的结论；谢邦昌和游涛(2015)[17]研究了中信行业指数网络在金融危机前、中、后三个阶段的联动效应及其社团结构，发现危机期间的网络联动效应最强；刘井建等(2015)[18]发现证券市场不同行业的风险联动具有非线性特征,金融危机冲击后行业风险联动趋势增强,尤其是非线性的放大效应尤为突出；韦立坚等(2017)[19]利用计算实验生成各种风险“情景”,发现2015年中国股市流动性危机引起了个股板块联动和流动性缺失传染。

在对股票市场结构的研究中，股票相关分析是主要方法之一，也称为股市相关结构分析。一些文献采用随机矩阵理论与特征根“偏离”*偏离在本文中指的是经验数据相关矩阵的特征根大于随机矩阵理论谱分析特征根上界的现象。分析来研究其动态演变(Plerou等,2002; Han等,2017; Laloux等,1999; Plerou等,2001; Coronnello等,2007; Garas和Argyrekis,2007; Nakayama和Iyetomi,2009)[1,16,20-24]，也有部分研究利用偏离随机矩阵性质的特征向量分析来识别经济行业部门与部门内相关性分析(Coronnello等,2007; Garas和Argyrekis,2007; Gopikrishnan等,2001; Jiang等,2014)[22-23][25-26]及其结构稳定性(Gopikrishnan等,2001)[25]，但大部分文献的研究对象是欧美股市，利用随机矩阵理论对中国股市相关结构的研究成果非常有限。这其中Han等(2017)[16]虽然研究了我国股市在2007-2008年金融危机前与危机中沪深A股的分时数据的相关性结构变化，但未考虑金融危机后的股市相关性变化。同时，2015年的股灾的发生并非由于金融危机的冲击，也并未导致金融危机的发生，与2008年的情况存在明显差异，因此市场相关性结构的演变过程可能也有所不同。同时考虑股市相关结构的时变性，对中国股市相关结构的分析及其在股灾中的演变需要更深入的理论探讨与更为丰富的经验证据。

为了更深层次揭露股票之间的相关性，Nakayama和Iyetomi(2009)[24]、Kenett等(2015)[27]、Han等(2017)[16]引入去除市场趋势因素后的偏相关系数(Partial Correlation Coefficients)矩阵方法来研究其动态变化过程。Kenett等(2015)[27]通过偏相关分析发现，美国、英国、日本等发达市场的市场稳定程度比印度等发展中国家更高，而一种股票可能受到其主要部门分类之外的不同部门的影响。Han等(2017)[16]发现，与相关矩阵相比，偏相关矩阵显示的相关结构在金融危机前和危机期间的差距明显缩小。但已有研究均缺乏对股市相关结构动态演化过程中的稳定性特征的分析。稳定性特征是随时间变化而相对固定的市场相关结构特征，表明了拥有某些特征的个股之间存在相对稳定的关系，可能的特征包括行业、地域、市值大小等。比如张华勇(2014)[28]就认为由于信息不对称的存在，投资者无法得知某只股票的波动原因和范围，因此会猜想同行业的股票或同类性质的股票也会发生波动，从而做出相应的交易行为。

综合而言，基于随机矩阵理论，国内外围绕股市相关矩阵特征展开了大量的研究，但针对中国股市2015年股灾前、中、后三个阶段相关结构动态演变过程的研究较少，缺乏对股灾期间稳定性特征的深入分析。因此本文的研究将在一定程度上弥补现有研究的不足。

本文研究的主要贡献在于：第一，基于随机矩阵理论，从2015年股灾前、中、后三个阶段的中国股市相关结构“偏离”情况展开分析，揭示市场在三个阶段的相关结构差异；第二，基于偏相关系数矩阵方法，深入分析去除市场指数因素后股市相关结构主要特征的动态变化过程，并探讨了股灾期间仍然存在的稳定性特征；第三，考察了中国长期以来股市相关结构的动态演变过程。

三、 股市相关结构的定量测度理论

(一) 股票价格相关系数矩阵

对股票价格相关性的研究，由于普通收益率{(Si(t+Δt)-Si(t))/Si(t))}在股票上涨和下跌过程中存在价格变化的不对称性，通常会将收盘价通过以下方法转换为对数价格收益率(“对称的价格变化”)。

Gi(t):=lnSi(t+Δt)-lnSi(t)

(1)

其中Si(t)，表示股票i在第t期的收盘价。

在公式(1)的基础上，选取N只股票T时期的收益率进行相关性分析(T远大于N)。同时，考虑到不同的股票之间，波动幅度存在显著差异，研究将收益率数据进行标准化处理。

(2)

由此，可以计算出N只股票T期的收益率的相关系数矩阵C，矩阵的元素为股票i和j在时间区间T中的相关系数，表示为：

Cij=E[gi(t)gj(t)]

(3)

由式(2)、(3)可知，Cij∈[-1,1]。当Cij=1时，表明两只股票完全线性相关(同时上涨且上涨幅度相同)；当Cij=-1时，表明两只股票价格变化完全线性负相关(一只上涨，另一只则下跌，且幅度相同)；当Cij=0时，表明两只股票价格变化不存在线性相关性。因此，相关系数矩阵可以表示为：

(4)

其中，G为N行T列矩阵，元素为{gi,t=gi(t);i=1,…,N;t=0…,T}，GT代表G的转置。

(二) 经典随机矩阵理论

由于实际股票对数价格收益率的时间样本区间T是一段有限时间跨度，在进行平均化处理过程中会导致测量误差。为了探讨股票价格波动是否是完全随机过程，本文采取经验数据相关系数矩阵与随机矩阵理论(RMT)特征相比较的方法，构建同样维度的随机序列相关系数矩阵作为对照研究，来与经验数据相关系数矩阵进行比较分析。构建的随机序列相关系数矩阵如下：

(5)

其中，A为N行T列矩阵，包含的元素为N个T长度的随机序列(每个随机序列的均值为0，方差为1)，因此可以认为N个序列之间是独立的。AT代表A的转置。

基于此，计算矩阵R的非对角线元素{Rij;i≠j}的概率分布P(Rij)、均值E(Rij)，以及特征根λR。

根据RMT，当N→∞和L→∞，且Q≡T/N>1固定时，依照Marcenko-Pastur法则(Marcenko和pastur,1967;Bai,1999; Bai等,2009)[29-31],可以由公式(6)推导出理论上矩阵R的特征根的概率分布Prm(λ)。

(6)

其中，矩阵特征根λ的值位于λ+和λ-之间，而λ+和λ-分别是RMT谱理论特征根的最大值(上界)和最小值(下界)，其计算公式如下：

(7)

(8)

基于上述理论研究，在经验数据实证分析中，研究将矩阵C的非对角线元素{Cij;i≠j}的概率分布P(Cij)、均值E(Cij)，以及矩阵C的特征根λ、特征向量u的概率分布与矩阵R的实际数据进行比较，并分别考察两者相对于与RMT特征根分布、特征向量分布的偏离情况，分析中国股票市场相关结构中的“噪声”与“市场信息”。

(三) 偏相关系数矩阵

根据已有相关文献研究(Han等,2017;Nakayama等,2009)[16，24]，对于任意股票的收益率时间序列，都可以通过下述线性回归方程得到其自身的特异性εi(t)。

Gi(t)=αi+βiGmarket(t)+εi(t)

(9)

其中Gmarket(t)，代表上证指数对数收益率。本文以εi(t)代替Gi(t)构建偏相关系数矩阵C′。

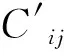
(10)

其中，σεi和σεi代表εi(t)和εj(t)的标准差。相对简单的偏相关系数计算方法可表达为下式(Baba等,2004;Kenett等,2010)[32-33]：

(11)

其中，Cim代表Gi(t)与Gmarket(t)的相关系数，Cjm代表Gj(t)与Gmarket(t)的相关系数。

通过上述计算过程得到的是去除了市场趋势信息影响的股票对数价格收益率偏相关系数矩阵，将该矩阵与前面两类相关系数矩阵进行比较，可以更好地考察市场相关性结构中包含的市场信息及其在股灾前后的演变过程。

四、 中国股市相关结构的动态演变过程与稳定性特征分析

(一) 样本数据

根据研究的需要，实证分析所采用的数据分为两个部分：

第一，为了验证我国股票市场各股票之间的相关性是否随时间变化，以及价格波动中是否存在“市场信息”，研究选取上证A股N=702只股票，从2014年7月至2017年6月共36个月的5分钟、60分钟的对数价格收益率。其中，设定2014年7月至2015年6月为股灾前、2015年7月至2016年6月为股灾期间、2016年7月至2017年6月为股灾后。

交易数据预处理过程中，剔除了以下股票：(1)2015年以后上市的股票；*2016年上市的股票，在本文研究时间区间通常会有大量一字涨停日，不适合进行5分钟收益率分析。(2)三个区间内价格缺失分别超过30%的股票，如较长时间停牌股。此外，对于各股票对数价格收益率缺失的部分，在计算相关系数矩阵时不纳入考虑。

数据来源于同花顺iFinD数据库。

(二) 股灾期间市场相关结构的动态演变

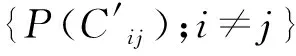
从图1中(纵轴为对数化坐标)可以看出：

(1)股票市场相关系数的分布P(Cij)并不对称，以正平均值为中心(E(Cij)>0)，这意味着我国股票市场上正相关价格波动比负相关价格波动更为普遍。特别是在股灾期间，所有的Cij均大于零。

(2)以5分钟交易数据为例，股灾前的相关系数均值(E(Cij)=0.24)，明显低于股灾中的相关系数均值(E(Cij)=0.45)，但显著高于股灾后的股市相关系数均值(E(Cij)=0.14)。此外，这三个时间区间的股票相关系数分布的标准差也有显著差异(表1)，表明股票之间的相关性并非固定不变，而是具有时变性，与国内外相关研究结果相符。特别是在股灾发生期间，个股之间价格相关性远高于股灾前后。

(3)将通过公式(5)构建的随机序列相关系数矩阵R引入分析作为矩阵C随机部分的对照矩阵，构成了图中均值为0的对称曲线和曲线下方面积。对比P(Cij)和P(Rij)，可以发现股票市场的负相关部分{P(Cij);Cij<0}，较多地被控制在P(Rij)的阴影面积中，因此可以认为观测到的股票之间的负相关关系大部分是随机效应导致。同时，股灾中市场相关结构与P(Rij)基本无重合且均大于0，也说明这一时期股市价格波动更为趋同。此外，我国股票市场结构与美国股票市场相比(Plerou等，2002)[1]，反映的股市整体价格变动与投资者群体行为更趋于一致性，存在更大的相关系数。

图1 相关系数概率分布比较

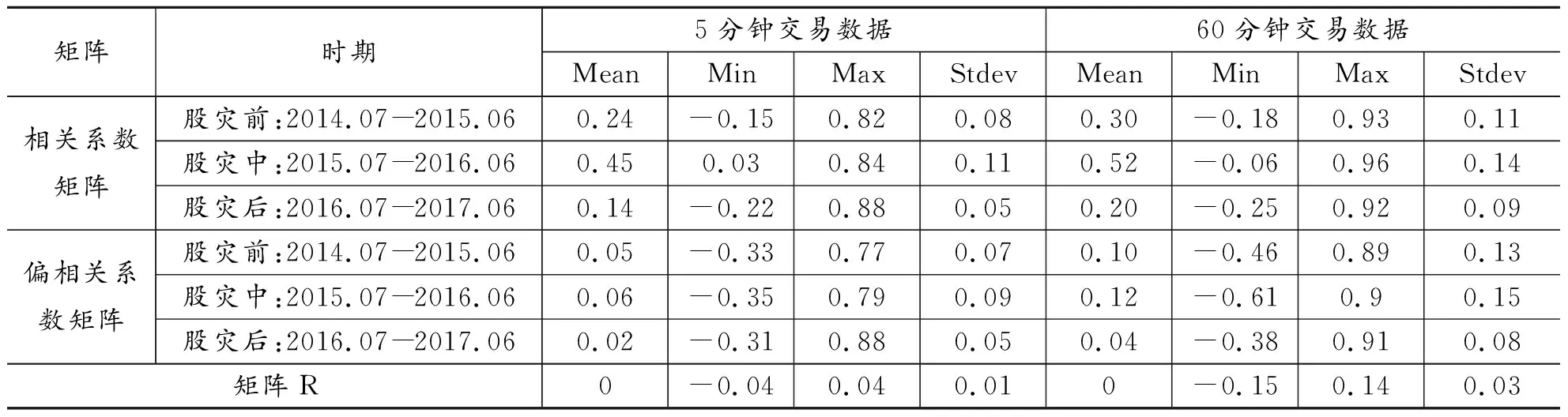
矩阵时期5分钟交易数据60分钟交易数据MeanMinMaxStdevMeanMinMaxStdev相关系数矩阵偏相关系数矩阵股灾前:2014.07-2015.060.24-0.150.820.080.30-0.180.930.11股灾中:2015.07-2016.060.450.030.840.110.52-0.060.960.14股灾后:2016.07-2017.060.14-0.220.880.050.20-0.250.920.09股灾前:2014.07-2015.060.05-0.330.770.070.10-0.460.890.13股灾中:2015.07-2016.060.06-0.350.790.090.12-0.610.90.15股灾后:2016.07-2017.060.02-0.310.880.050.04-0.380.910.08矩阵R0-0.040.040.010-0.150.140.03

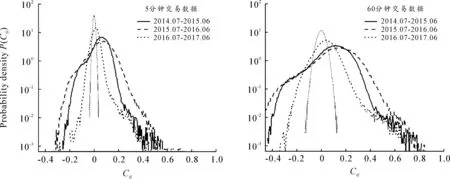
图2 偏相关系数概率分布比较

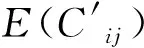
通过比较图1、图2和表1的结果，可以认为分别以5分钟和60分钟交易数据构建的相关系数矩阵和偏相关系数矩阵，在股灾前、中、后三个阶段所具有的特征变化基本相同。因此文中后续分析将以包含更多市场信息的5分钟数据相关系数矩阵作为主要研究对象。

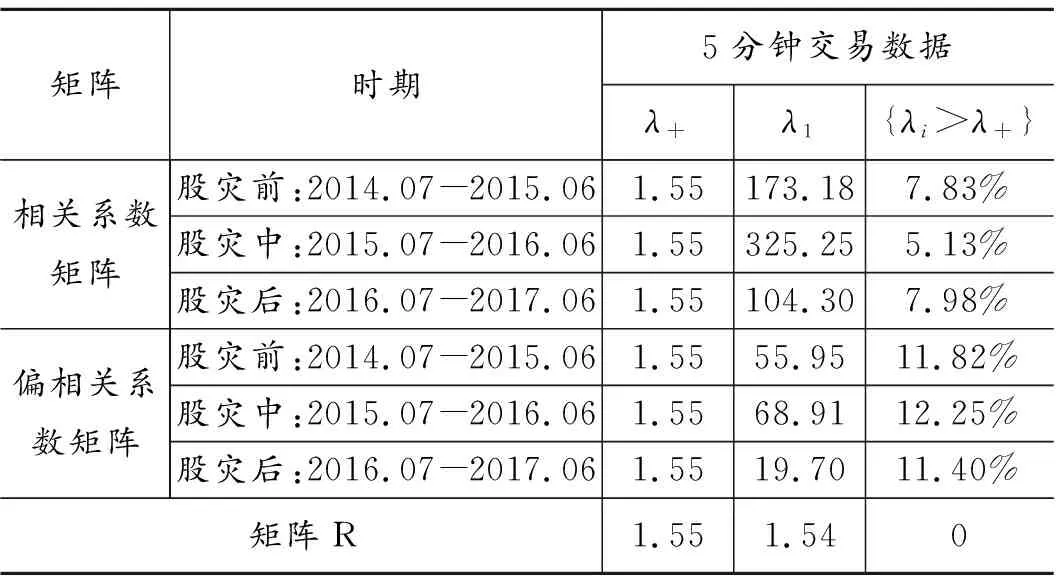
表2 相关系数矩阵的特征根偏离现象

2.股市相关结构“偏离”RMT谱分布的动态分析。(1)特征根偏离情况分析。表2显示，股票市场经验数据相关系数矩阵C的最大特征根λ1远远大于随机序列相关矩阵R，以5分钟交易数据相关系数矩阵的特征根为分析对象，股灾前偏离(这里仅考虑大于的情况)λ+的比例为7.83%，股灾中为5.13%，股灾后为7.98%，三个时期市场相关系数矩阵的最大特征根从大到小的顺序为股灾中、股灾前和股灾后，也说明“市场信息”对股票的共同影响因素始终存在；而去除最主要的市场趋势信息后，三个阶段相关矩阵的最大特征根均大幅缩小，但偏离特征根比例却有所增加。因此有必要对经验数据和随机数据两类相关系数矩阵的特征根分布进行比较分析，并分别考察三个时期经验数据相关系数矩阵的特征根相对于由公式(6)得到的RMT特征根分布Prm(λ)的偏离情况，其中由公式(7)得到的理论特征根区间为[λ-=0.57,λ+=1.55]。

在图3中，研究将5分钟交易数据相关系数矩阵C与矩阵R的特征根分布分别与通过式(6)计算出的特征根分布Prm(λ)进行对照比较，发现两者存在显著的差异。

①在图3(a)、(b)、(c)中，将基于股灾前、股灾中和股灾后三个时期的702只股票收益率构建的相关系数矩阵C的特征根分布Pc(λ)与RMT特征根概率分布Prm(λ)进行比较，发现C的特征根大部分与Prm(λ)一致，表明通过与矩阵R的特征根相关性的一般特征进行比较，可以更准确地理解真实数据的随机结构。同时，也显示一些较大的特征根偏离了λ+，可以认为是“市场信息”，即市场趋势信息对所有股票价格的影响。(a)、(b)、(c)中右侧的内图为经验数据相关系数矩阵C的特征根的直方图，并标注了最大特征根，三个阶段的特征根均远大于RMT特征根上界λ+。同时，可以看到，股灾中的特征根分布偏离现象最为严重，股灾后偏离程度最轻。

图3 相关系数矩阵与随机矩阵特征根概率分布比较

②图3(d)显示，基于N=702和T=11760构建的互不相关的随机序列相关系数矩阵R的特征根概率分布Pr(λ)的曲线始终围绕Prm(λ)上下波动，曲线下方面积基本重叠，其特征根位于区间0.57≤λR≤1.54。可见，对于一个白噪声序列，无论其特征根的分布还是特征根取值区间均未出现偏离现象，与RMT谱分布一致，即MP分布。

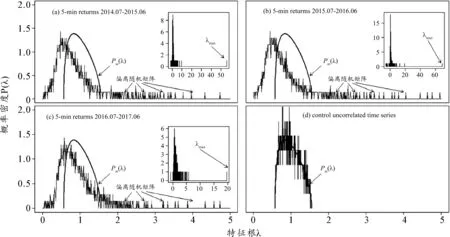
图4 偏相关系数矩阵与随机矩阵特征根概率分布比较

图4中显示，偏相关系数矩阵C′的特征根偏离情况显著降低，但偏离情况仍存在。这说明市场指数影响是导致市场相关性结构偏离随机过程的主要原因，但同时相关系数矩阵中还存在其他非随机市场信息特征。股灾期间，特征根分布的偏离程度仍然最明显，但与相关系数矩阵最大特征根相比差距显著缩小了，说明去掉的市场趋势信息中包含了股灾的主要描述特征，剩余的偏离特征根中仅留存相对少量的市场结构特征。

(2)经验相关系数矩阵特征向量“偏离”情况分析。为了深入分析股票相关系数矩阵C的特征根中大于λ+的部分,图5进一步显示了基于2014年7月至2015年6月的702只股票的5分钟对数价格收益率构建的相关系数矩阵C的特征向量的分布ρ(u)相对于公式(8)得到的RMT特征向量分布ρrm(u)(即高斯分布)的偏离情况。

①图5(a)显示，当C的特征根{λ:λ-λ<λ+}时，所对应的特征向量的分布较好地拟合了RMT特征向量分布曲线(图中实线)。

②图5(b)(c)中ρ(u)的特征向量分别为u(5)和u(2)，对应的C的特征根为λ(5)和λ(2)，均大于RMT特征根上界λ+，可以发现这两个特征向量的分布已经偏离了高斯分布。

③图5(d)显示是特征向量u(1)的分布，对应的是矩阵C的最大特征根，该分布显著偏离了高斯分布。

从ρ(u(1))可以发现，该特征向量的分布相当狭窄，所有股票的特征贡献几乎相等，表明这一特征向量代表了所选股票价格共同行为模式。这种模式也被称为“市场趋势”(Nakayama和Iyetomi, 2009)[24]。

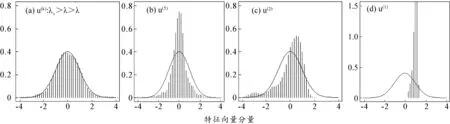
图5 经验数据相关矩阵与随机矩阵特征向量概率分布比较

(三) 股市相关结构的稳定性特征分析

1.特征向量u(1)与市场指数的稳定关联。通过比较由股灾前、中、后三个阶段的最大特征根对应的特征向量u(1)定义的投资组合*将最大特征根对应的特征向量的元素变换为和为1的权重向量，计算出按照该权重赋权的702只股票的投资组合的整体价格变化数据。与上证指数的5分钟对数价格收益率，均得到0.90以上的相关系数，并显示出良好的一致性和回归拟合效果(见图6、表3)。

因此可以认为对应于最大特征根的特征向量u(1)代表了股市对所有股票价格的共同影响，与Gopikrishnan等(2001)[25]对美国股票市场分析结果类似。这也说明了市场指数因素始终反映了股市相关结构的最主要特征。

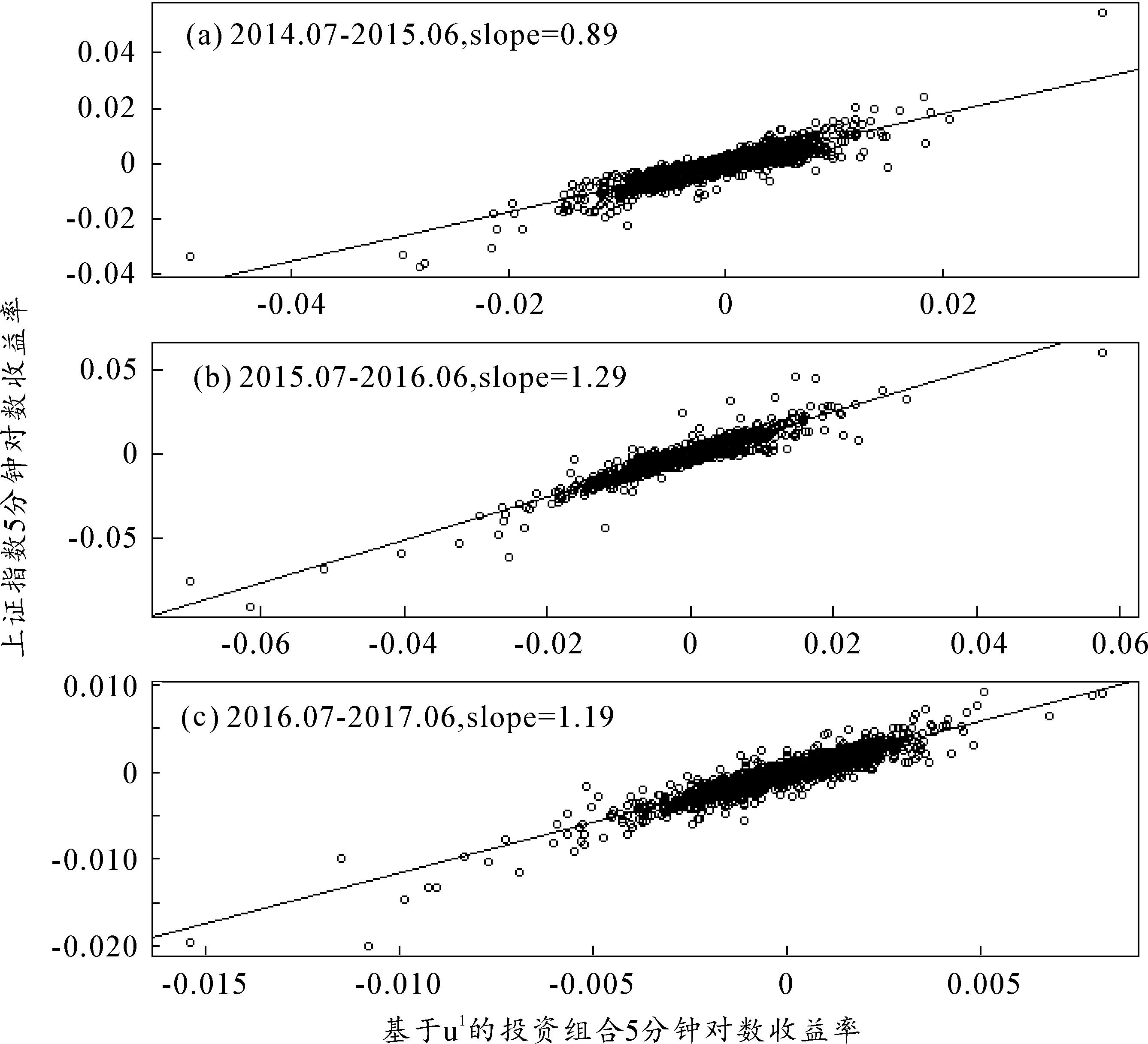
图6 u(1)定义的投资组合与上证指数的5分钟对数价格收益率比较

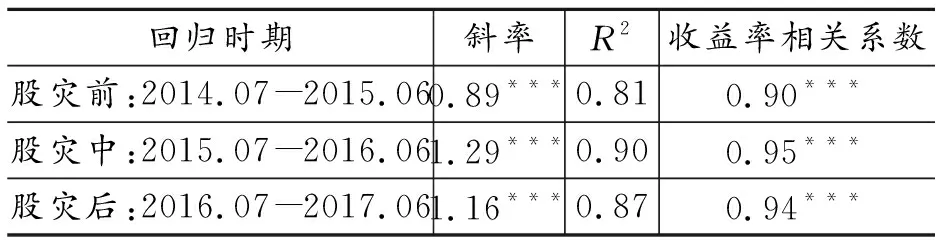
回归时期斜率R2收益率相关系数股灾前:2014.07-2015.060.89***0.810.90***股灾中:2015.07-2016.061.29***0.900.95***股灾后:2016.07-2017.061.16***0.870.94***

注:***表示系数在0.1%水平显著。

2.特征向量的跨期稳定性特征。为了进一步认识股灾期间的市场结构，本文考察了5分钟交易数据相关系数矩阵和偏相关系数矩阵的最大的5个特征根所对应的特征向量的稳定性，同时地也对照考察了60分钟交易数据相关系数矩阵的最大5个特征根对应的特征向量的跨期稳定性。

图7中显示了三个阶段相关系数矩阵的u(1)-u(5)五个特征向量的比较结果，其中第一层是股灾前702只股票对应的特征向量值，第二层显示的是股灾中，第三层显示的股灾后。可以明显看出，三个阶段的u(1)存在一定相似性且所有特征向量分量的方向均一致，u(2)-u(5)具有明显的变化，u(2)在股灾前和股灾中具有一定程度的相反变化倾向，而股灾前和股灾后却具有类似的分布。

图8更清晰地显示了三个阶段之间702只股票的最大五个特征向量之间相关性的变化。其中(a)(b)(c)三类时间区间比较相关系数矩阵特征向量相关图显示：①u(1)代表的市场趋势对所有股票的共同影响随着时间推移显示出较弱的稳定性特征；②u(2)代表的股市结构特征对所有股票的影响，在股灾中与其他时期相比呈现显著的负相关关系，股灾前与股灾后则为正相关。而(d)(e)(f)三类时间区间比较偏相关系数矩阵特征向量相关图则显示出：①u′(1)随着时间推移显示出较强的稳定性特征；②u′(2)在股灾前和股灾中仍然呈现显著的正相关关系，股灾前与股灾后则无明显相关性；③u′(3)-u′(5)在三个阶段均未表现出一致的稳定相关关系。图9中60分钟交易数据构建的偏相关系数矩阵，同样显示u′(1)随着时间推移显示出较强的稳定性，说明这一主要稳定性特征并未受到股市微观结构噪声的影响。

图7 5分钟对数价格收益率三个阶段的时间演变过程

图8 5分钟对数价格收益率特征向量的三个阶段相关系数图

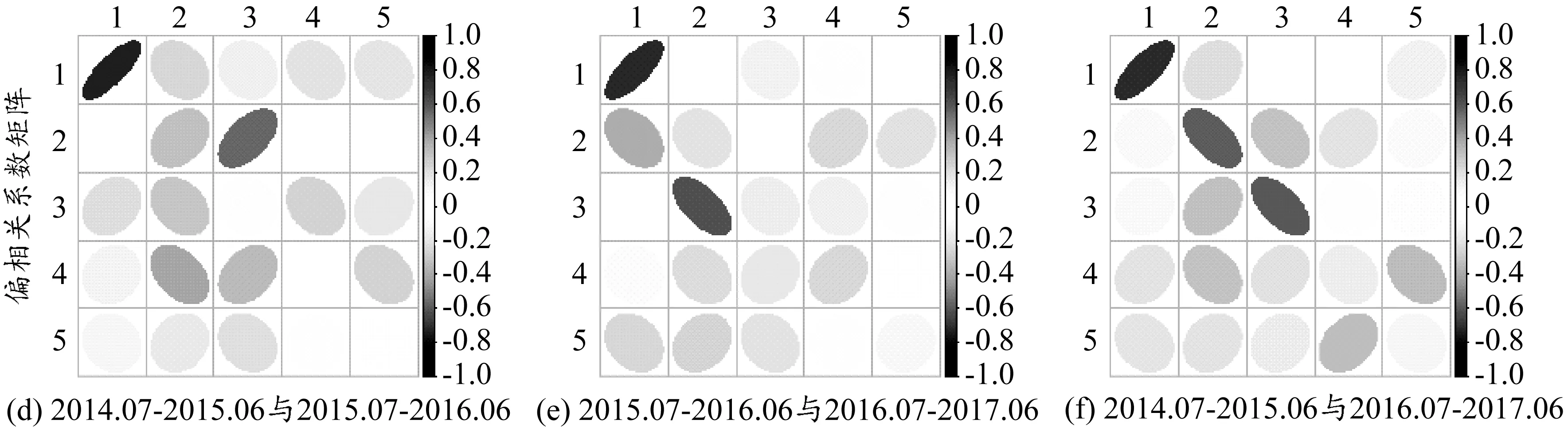
图9 60分钟对数价格收益率偏相关系数矩阵特征向量的三个阶段相关系数图

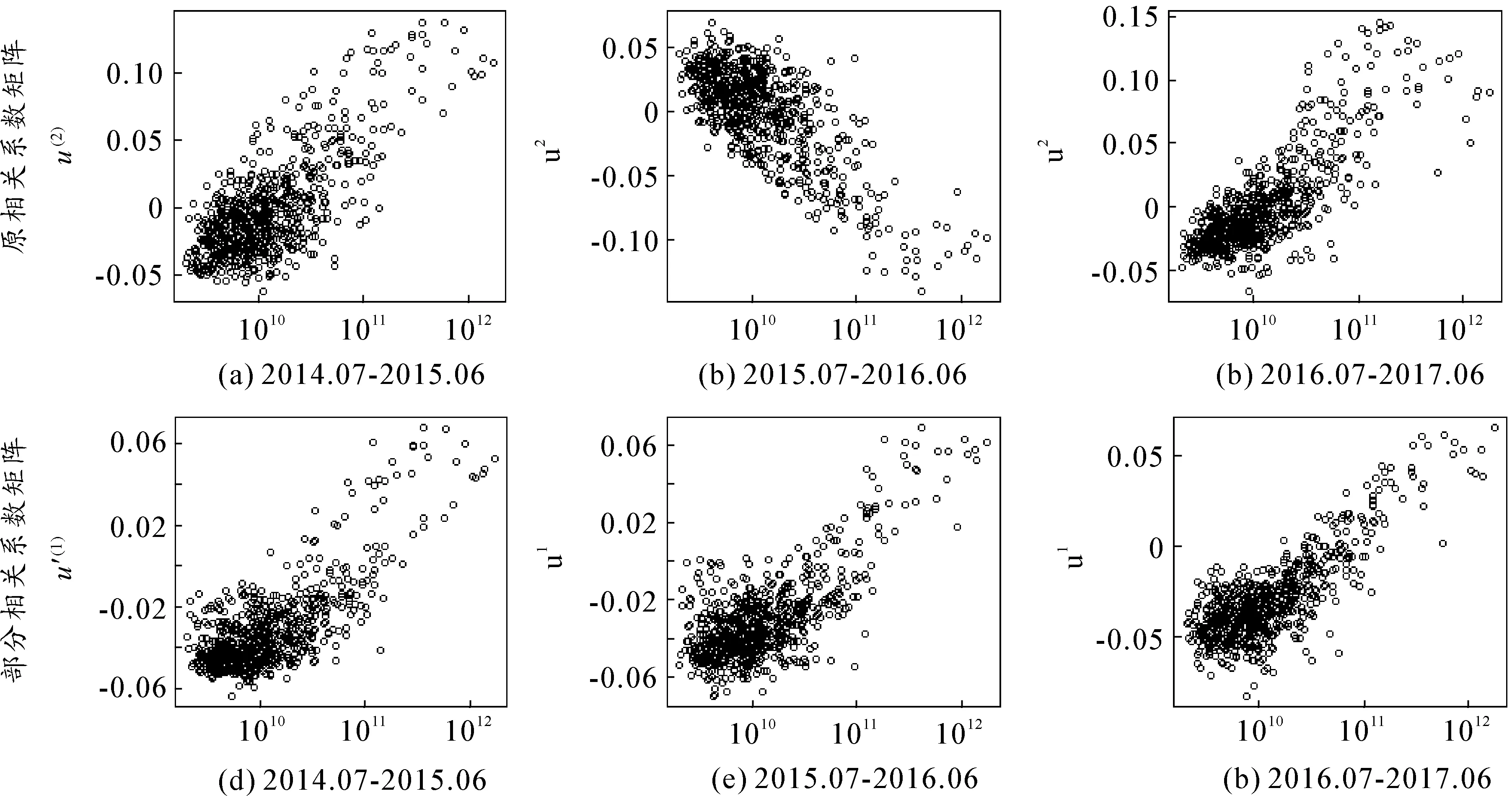
图10 5分钟对数价格收益率三个阶段的特征向量与股票市值散点图

图10显示的5分钟交易数据三个阶段的偏相关系数矩阵第二大特征根对应的特征向量u(2)和偏相关系数矩阵最大特征根对应的特征向量u′(1)，分别与股票市值的关系，横坐标是对数形式。可以看出，相关系数矩阵中，股灾前和股灾后，市值越大的股票，对应的u(2)越大；而股灾中则正好相反，市值越小的股票，对应的u(2)越大。当去除市场趋势信息后，本文用偏相关系数矩阵的最大特征向量u′(1)来替代相关系数矩阵的u(2)，结果显示三个阶段表现出稳定性结构特征，均为市值越大，对应的u′(1)分量越大(即特征贡献越大)。

上述研究说明，市场指数是股市相关结构变化的重要影响因素，而个股市值则是相关结构中去除市场指数因素影响后的稳定性影响因素。包含其余“市场信息”的特征向量则在三个阶段呈现出不稳定相关性或弱相关性，不适合从长期来解释股票溢价。但股灾前与股灾中u′(2)的显著相关性在一定程度上说明市场活跃繁荣时期与随后的市场大幅下跌时期存在部分相同的相关结构特征，很可能是两个时期内某个行业内部的股票之间始终存在显著相关性。特别地，比较股市相关结构的第二大特征根对应的特征向量u(2)与偏相关结构的最大特征根的特征向量u′(1)在股灾中完全相反的表现，说明市场不同市值股票之间联动的方式在股灾中发生了显著变化。

(四) 股市结构长期演变过程分析

从图3-图6中经验数据相关系数矩阵C的最大特征根和特征向量相对于RMT谱分布的偏离程度以及与偏相关系数矩阵的差异来看，相关系数矩阵最大特征根本身的大小反映了研究所选股票的共同价格变动的一致性程度，可以通过分析最大特征根的时间演化来考察股市长期结构变化。本文考察了1998年1月到2017年5月342只股票的日交易对数价格收益率的相关系数均值和矩阵最大特征根与上证指数波动率的动态演变过程。其中342×342相关系数矩阵C的计算采用的滑动时间窗口为500个交易日，并在其后10个交易日采用相同的最近期计算得到的相关系数均值和最大特征根。此外，为了方便显示，图11中各指标都做了一定尺度的变化。

图11显示了342只股票相关系数矩阵的最大特征根λmax与上证指数波动率的时间演变历程，底部的曲线是基于40个交易日的对数价格收益率计算的上证指数波动率。上证指数波动率在2008年大幅上升，对应于全球金融危机冲击下中国的股灾，当时市场上的所有股票几乎同时失去价值，价格大幅下跌，即所有股票价格波动都比其他时期更趋于一致。可以看到在这一时期相关系数均值E(Cij)与最大特征根λmax上涨超过一倍。类似地，在2015年由于前期资金杠杆的广泛使用及后续的清查场外配资，使股市陷入流动性危机，也经历了一轮暴涨暴跌，而这一时期，相关系数均值E(Cij)与最大特征根λmax同样快速上涨。

图11 上证指数波动率与矩阵C的均值、最大特征根动态演变过程

五、 结论与建议

通过本文研究可以看出，中国股票市场相关结构整体而言随时间动态演变，但也存在稳定性特征。具体而言，研究通过将2014年7月至2017年6月三年分为股灾前、股灾中和股灾后三个阶段，对中国上证A股702只股票构建的5分钟高频交易数据相关系数矩阵C的元素、特征根与部分偏离的特征向量分布，得出以下结论：

第二，三个阶段之间，相关系数矩阵C的均值、最大特征根均显示出明显差异，与偏相关系数矩阵C′均值与最大特征根的较小差异对比，说明中国股市相关结构与美国一样，具有动态时变性，但这种时变性主要体现在市场趋势上，去除了主要市场因素后，股灾前与股灾中的市场相关结构非常相似。

第三，矩阵C的部分特征根大于RMT特征根区间且{λ1≫λ+}，部分“偏离”的特征向量的与高斯分布呈现显著差异，同样表明了在中国股市相关结构中存在显著的“市场信息”。而在三个阶段中，由最大特征根u(1)定义的投资组合收益率均与上证指数收益率之间存在较高的相关性和回归拟合优度，也验证了这一点。

第四，股灾中的相关系数矩阵C的均值、最大特征根以及特征根分布的“偏离”程度均远大于其他两个时期，市场趋势对所有股票的共同影响仅为弱稳定性。但股灾中股票市值与第二大特征根对应的特征向量的相互关系发生了明显的翻转。在股灾前后,经济基本面、行业周期等不太可能出现剧烈变化，相关性却显著改变，说明股灾前和股灾中个股之间出现了明显的“过度联动”。而“过度联动”会导致当危机发生时，个股板块之间的联动性再次大幅提升，即使采用分散投资策略，也难以有效规避市场整体下跌的趋势(马丹等，2016)[13]。

第五，去除市场指数因素后，构建的偏相关系数矩阵的最大特征根对应的特征向量在三个阶段呈现出显著相关性和稳定性，且个股特征向量元素值与股票市值正相关。这说明股市中存在稳定的市值效应，不考虑市场指数因素时，这种效应会长期稳定存在。结合结论一，说明危机发生时，板块间传染效应的迅速增加导致的联动性的大幅提升，仍是主要受到市场指数因素的影响。

此外，基于对股市相关结构的研究，本文进一步考察1998年1月至2017年5月上证指数波动率与相关系数矩阵的均值E(Cij)与最大特征根λmax的动态演变过程，发现：第一，在经济危机期间，中国股市也与国外一样显示出快速上涨的最大特征根和相关系数均值；第二，由于相关系数矩阵采用的过去500个交易日的收益率，与波动率的比较中存在一定滞后性，在数据上显示2015年7-9月当E(Cij)与λmax显著上涨发生在股灾发生之后的一段时间，表明相关系数矩阵的偏离的确反映了股票市场趋势信息。

根据上述结论，研究建议：(1)对于市场监管者而言，在进行股票市场风险的管理中，有必要考虑股市相关结构的动态演化过程。比如当股市相关性较高且趋于上升时，表明市场风险在增加，监管者可以设置一系列股市相关结构预警参数，采取措施将股票收益率之间的相关性维持在安全范围内。(2)对于股票投资者而言，在进行投资策略和风险管理中，应将股市相关结构的动态演变和稳定性特征纳入考虑。比如当股票市场相关结构与随机序列相关结构拟合较好时，股票收益率近似为随机过程，技术分析等积极投资策略将缺乏有效性，指数投资将是较好的策略，市场风险相对较小；当股票市场相关结构偏离随机矩阵理论谱分布时，市场内部存在较大正相关性，积极投资策略将更容易获得超额收益或更大的损失，同时市场的风险也在增加。中国股市长期存在较高的内部相关性，特别是在金融危机和股灾期间，指数投资或许并非较好的选择，而极端波动也时有发生；但去除市场指数因素后所显现的股票市值对偏相关系数矩阵的最大特征贡献的稳定性，说明应存在根据股票市值构成的长期有效的积极投资策略。

[1]PLEROU V,GOPIKRISHNAN P,ROSENOW B,et al.A random matrix theory approach to quantifying collective behavior of stock price fluctuations[C]//HIDEKI TAKAYASU.Empirical Science of Financial Fluctuations.Tokyo:Springer,2002:35-40.

[2]陈华.股灾的成因分析及对策思考[J].淮海工学院学报(人文社会科学版),2015(10):91-93.

[3]杜军.股灾期间行业板块间的相关结构研究[D].成都：西南财经大学统计学院,2016.

[4]谢百三,童鑫来.中国2015年“股灾”的反思及建议[J].价格理论与实践,2015(12):29-32.

[5]张亦春,周颖刚.中国股市弱式有效吗?[J].金融研究,2001(3):34-40.

[6]陈灯塔,洪永淼.中国股市是弱式有效的吗——基于一种新方法的实证研究[J].经济学(季刊),2003(4):97-124.

[7]吴振翔,陈敏.中国股票市场弱有效性的统计套利检验[J].系统工程理论与实践,2007(2):92-98.

[8]马向前,任若恩.基于市场效率的中国股市波动和发展阶段划分[J].经济科学,2002(1):66-72.

[9]高蓉,周爱民,向兵.股市动态弱式有效性研究——基于滚动广义谱方法[J].投资研究,2012(12):137-147.

[10]张鹏.中国股市弱式有效的重新检验——基于高频交易策略的超额收益[D].昆明：云南财经大学金融学院,2016.

[11]屈博,庞金峰.有摩擦条件下中国股票市场的弱式有效性研究[J].金融与经济,2016(3):73-78.

[12]刘维奇,刘新新.个人和机构投资者情绪与股票收益——基于上证A股市场的研究[J].管理科学学报,2014(3):70-87.

[13]KALLBERG J,PASQUARIELLO P.Time-series and cross-sectional excess comovement in stock indexes[J].Journal of Empirical Finance,2008,15(3):481-502.

[14]MARKOWITZ H.Portfolio selection[J].Journal of Finance,1952,7(1):77-91.

[15]马丹,刘丽萍,陈坤.关联效应还是传染效应[J].统计研究,2016(2):99-106.

[16]HAN R Q,XIE W J,XIONG X,et al.Market correlation structure changes around the great crash:a random matrix theory analysis of the Chinese stock market[J].Fluctuation and Noise Letters,2017,16(2):1-6.

[17]谢邦昌,游涛.金融危机前后中信行业指数联动效应及其社团结构比较[J].商业经济与管理,2015(1):80-87.

[18]刘井建,焦怀东,南晓莉.危机冲击背景下股票市场风险联动非线性[J].系统工程,2015(12):16-22.

[19]韦立坚,张维,熊熊.股市流动性踩踏危机的形成机理与应对机制[J].管理科学学报,2017(3):1-23.

[20]LALOUX L,CIZEAU P,BOUCHAUD J P,et al.Noise dressing of financial correlation matrices[J].Physical Review Letters,1999,83(7):1467-1470.

[21]PLEROU V,GOPIKRISHNAN P,ROSENOW B,et al.Collective behavior of stock price movements——a random matrix theory approach[J].Physica A Statistical Mechanics & Its Applications,2001,299(1/2):175-180.

[22]CORONNELLO C,TUMMINELLO M,LILLO F,et al.Economic sector identification in a set of stocks traded at the New York Stock Exchange:a comparative analysis[C].Proceedings of SPIE,Noise and Stochastics in Complex Systems and Finance,2007,6601(7):198-209.

[23]GARAS A,ARGYRAKIS P.Correlation study of the athens stock exchange[J].Physica A Statistical Mechanics & Its Applications,2007,380(7):399-410.

[24]NAKAYAMA Y,IYETOMI H.Random matrix theory of dynamical cross correlations in financial data[J].Progress of Theoretical Physics Supplement,2009,179(1):60-70.

[25]GOPIKRISHNAN P,ROSENOW B,PLEROU V,et al.Quantifying and interpreting collective behavior in financial markets[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2001,64(2):1-4.

[26]JIANG X F,CHEN T T,ZHENG B.Structure of local interactions in complex financial dynamics[J].Scientific Reports,2014(4):1-9.

[27]KENEET D Y,HUANG X,VODENSKA I,et al.Partial correlation analysis:applications for financial markets[J].Quantitative Finance,2015,15(4):569-578.

[28]张华勇.金融市场联动性和风险传染的内在机制研究[J].云南社会科学,2014(4):81-84.

[29]MARCENKO V A,PASTUR L A.Distribution for some sets of random matrices[J].Mathematics of the USSR-Sbornik,1967,1(4):457-483.

[30]BAI Z D,Methodologies in spectral analysis of large dimensional random matrices,a review[J].Statistica Sinica,1999,9(3):611-662.

[31]BAI Z D,FANG Z B,LIANG Y C.Spectual theory of large dimensional random matrices and its applications to wireless communications and finance statistics[M].Hefei:University of Science and Technology of China Press,2009:22-28.

[32]BABA K,SHIBATA R,SIBUYA M.Partial correlation and conditional correlation as measures of conditional independence[J].Australian & New Zealand Journal of Statistics,2004,46(4):657-664.

[33]KENETT D Y,TUMMINELLO M,MADI A,et al.Dominating clasp of the financial sector revealed by partial correlation analysis of the stock market[J].Plos One,2010,5(12):1-14.