基于模糊度量视觉特征的非局部均值去噪

吕俊瑞，罗学刚,，岐世峰,彭真明

(1.攀枝花学院 数学与计算机学院, 四川 攀枝花 617000;2.电子科技大学 信息与通信工程学院，成都 610054)

0 引 言

图像是人类获取和传递信息的重要手段。在获取、传输和记录过程中，由于各种客观因素将大量噪声信号叠加在图像里，造成图像质量的退化。合理地剔除妨碍人眼感知图像的噪声，又保留图像优良的结构、纹理细节是图像去噪的难点。

多年来，学者们为了解决该难题，提出了许多方法，如高斯滤波、中值滤波和小波阈值去噪等。这些方法实现简单，但容易造成在去除噪声同时将图像细节信息丢失, 去噪结果不能获得令人满意的效果。近年来，涌现出一系列较好性能表现的新型去噪算法。如各向异性过滤(anisotropic filtering，AF)[1]、全变法(total variation，TV)图像去噪[1]、非局部均值去噪(non-local means, NLM)去噪[2]、双边滤波去噪(bilateral filtering，BF)[3]、三维块匹配(block matching 3D，BM3D)去噪[4]等。这些优秀的算法中，Buades等提出的非局部均值(non-local means, NLM)算法在图像去噪方面获得了重要研究成果，在领域内有较大的影响，得到大量学者的关注。

传统的去噪算法以像素为单位获取去噪估计值，而NLM去噪算法是以图像块为基本单元，由于图像内的图像块存在较多的结构相似性, 较好地利用了图像块结构信息，以像素块灰度值相似性为权重进行加权平均来估计对应像素的真实值。由于图像块能更好地体现图像结构信息，表现出较强的去噪性能。NLM方法去噪性能优越，但存在运算量巨大和参数选取不稳定的问题，难以达到最优去噪效果和实际工程应用。为此，很多学者对NLM提出了优化策略，这些方法主要集中在降低计算复杂度、参数优化和融合其他算法以提升去噪性能3方面开展[5]。

分析发现，NLM计算量大的主要原因是每个像素都要和区域内其他像素块进行欧式距离和高斯核函数计算。另外，欧式距离是直接计算图像块间的相似性，其实并未真正考虑图像结构信息，不是合适的图像结构度量方式，影响NLM去噪性能，并且计算量大。因此，本文针对NLM采用欧式距离相似性度量不够准确的问题，提出一种利用模糊度量的视觉特征相似度作为衡量图像像素点相似性的NLM图像去噪算法。

1 NLM去噪算法

图像噪声模型可以描述为

y=z+ν

(1)

(1)式中：z为以向量形式表示的真实图像；ν为标准差σ2的加性高斯白噪声；y为观测图像。

NLM去噪是图像区域内相似图像块的相似度为线性系数的加权滤波器，将观测图像y映射成为最终去噪图像NLM(y),其定义表示为

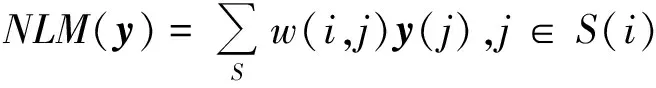
(2)

(2)式中：y(i)为图像y中位置为i的灰度值；S(i)表示以位置i为中心的s×s区域；w(i,j)为分别以位置i和j为中心的图像块灰度值相似性权重函数，定义为

(3)

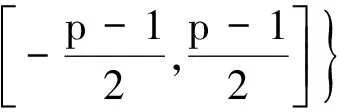
(4)

w(i,j)的计算是NLM的核心，Ga是为了突出图像块中心像素的作用，增强可靠性。但实验证明,Ga的存在对改善NLM去噪算法的去噪效果不明显。

经实验和理论证明，NLM去噪是一种性能较优的图像去噪方法[2]。但NLM图像去噪算法运算量大, 对像素大小为M×N的图像, 计算复杂度为O(MNp2S2)。为了加快运算速度，大量文献提出了加速策略[5]。这些方法的主要思想以降维处理来降低运算量，但降维过程本身就需要大量的运算[6]。

2 基于模糊度量的视觉特征相似性

相似性度量的合理选择是NLM算法良好性能实现的关键，文献[7]利用马氏距离代替欧式距离来度量图像块的相似度，需要奇异值分解，时间复杂度较高。

2.1 模糊度量定义

在模糊拓扑中最重要的问题是得到一个合适的模糊度量的概念[8]。根据文献[8]的定义，首先描述模糊度量空间的概念。设X是一非空集合, *是连续的模，集合X上的一个模糊度量R：X×X×[0,]∈[0,1]，如果满足条件

1)R(x,y,t)>0；

2)R(x,y,t)=1,当且仅当x=y；

3)R(x,y,t)=R(y,x,t)；

4)R(x,y,t)+R(y,z,c)≤R(x,y,t+c)；

5)R(x,y,*):(0,)→[0,1]是连续的。其中，x,y,z∈X,t,c>0，则称(R,*)是关于集合X的模糊度量,使用(X,R,*)表示模糊度量空间[9]。在文献[8]中提出以下命题。

在模糊度量空间里命题已经在文献[9]中证明。

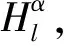
(5)

2.2 视觉特征相似度

尽管NLM取得了很好的去噪效果，但直接使用图像块灰度值进行欧式距离计算，没有很好地考虑到图像块的结构信息，导致对原图像的结构信息保护仍不够。从图像块结构和灰度两方面，本节提出以模糊度量构建具有视觉特征的相似度度量方法。

为了突出边缘信息在图像结构中的重要性，结合2.1节里描述的模糊度量命题，得到强调图像块边缘的简化模糊度量函数。

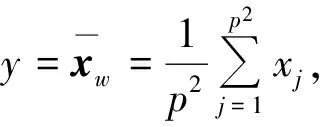
(6)

利用(6)式可以得到整幅图像的每个像素点的模糊度量值，取值为[0,1]，对应灰度图像t=255。

根据文献[12]，提出基于模糊度量的图像块间的灰度值分布和结构信息相似度描述。图像灰度值的分布是图像冗余结构重要的信息，(7)式描述了灰度值模糊度量函数。

HC(xi,xj)=1-|Cxi-Cxj|

(7)

(7)式中：Cxi=max(Hxi)-min(Hxi)表示图像块xi的模糊度量最大最小比较值；Cxj同理为图像块xj的模糊度量最大最小比较值；|·|为取绝对值。

结构模糊度量函数定义为

(8)

最终图像块xi和图像块xj的视觉特征相似度函数为

Dis(xi,xj)=(HC(xi,xj)Hs(xi,xj))

(9)

3 基于模糊度量视觉特征的NLM去噪

本节描述一种以平滑核函数计算相似性权重方法。该方法将相似性权重小的图像块摒弃掉，增强相似性高的权重系数，更好地帮助了图像结构信息的利用。

3.1 改进NLM去噪算法

为了让相似性高的图像块获得较高权重，改进后估计图像y中的图像块B的NLM去噪算法描述为

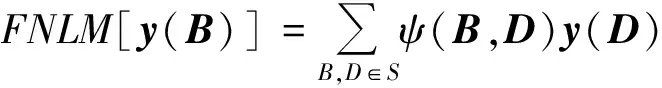
(10)

(10)式中，ψ(B,D)为图像块B与邻域内S的图像块D={D1,D2,…,Dn}的相似度权重，且满足0≤ψ(B,D)≤1。

文献[13]的实验证实高斯核函数对NLM去噪性能提高帮助不大，反而对于搜索区域较大的情况，效果会更差。同时，高斯核函数的滤波带宽参数h一直是NLM难以控制参数。为了提高去噪性能和降低计算复杂度，本文改进算法的权值函数采用平滑核函数代替高斯核函数，避免参数h设置带来的不稳定，定义为

ψ(B,D)=KFlat‖1-Dis(B,D)‖1

(11)

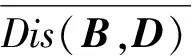
(12)

图1是对经典的Barbara图像采用统一的参数(S大小设置13×13,h=0.7×σ，p=5)进行的实验得出的权值分布图。从图1中不难看出，图1a高斯核函数对整体轮廓保留较好，但对于纹理细节丰富的部分(头巾、服饰)，欧式距离和高斯核函数不能很好地利用这部分结构信息；图1b由于采用模糊度量的结构相似度量方法和平滑核函数的权值函数，对结构信息强的图像块权值更高一些，对纹理区域自适应能力得到显著改善。

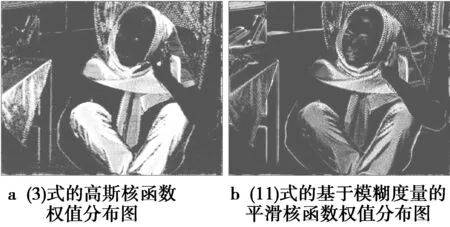
图1 加权函数效果比较Fig.1 Effect comparison of weighted function

3.2 算法步骤描述

改进NLM算法流程简述如下。

1)算法参数初始化，搜索区域的范围R和图像块大小B的设置。

2)针对椒盐噪声，利用中值滤波算法进行预处理。

3)计算图像的模糊度量。利用(6)式和查询矩阵得到整幅图像的模糊度量值。

4)计算视觉特征相似度。利用(7)式和(8)式分别将图像灰度模糊度量和结构模糊度量计算得到，利用(9)式计算得到图像块间的相似度距离。

5)计算估计值。根据(11)式和(12)式计算得到图像块间的权重系数，最后利用(10)式得到去噪图像点的估计值。

3.3 时间复杂度分析

整个算法的相似度权重计算分为图像的模糊度量值计算和图像块间的视觉特征相似度计算2部分。基于模糊度量的相似性度量是一种快速简便的计算方法，时间复杂度与图像大小成线性关系。整个图像的模糊度量H计算只需要2N×M次除法，2N×M次比较和N×M次求和操作。除法操作较为耗时，为了提高算法的效率，将(6)式中除法运算采用查表法优化。对于灰度图像，(6)式的分子和分母都将在[t,t+255]。确定t值后，将所有可能的分数枚举出来，构建查询矩阵，那么每次计算就只是查表即可。在Dell Inspiron,Core i3,2 GByte内存的笔记本上测试，构建该矩阵只需要0.015 s，而直接计算处理一幅600像素×800像素的图像，除法操作需要0.12 s，加速效率明显。求和操作可以参考文献[5]的图像积分图。模糊度量计算完成后，每个图像块间的视觉特征相似性计算只需要2次最大最小者操作、3次求和、3次减法，1次比较和2次乘法。传统的欧式距离计算量与图像块大小有直接关系，计算量由图像块大小决定。而本改进方法依赖图像块的计算较少，运算效率提升较大。

4 实验结果与分析

为了验证改进算法的性能，选用了4个公开测试图像Barbara, Couple, Lena和 Man进行实验。在实验中，从去噪性能和运算效率这2个方面考虑，本文改进方法分别与BM3D[4]，LG-NLM[6]和LR-NLM[14]共4种基于块相似性的去噪算法做定性比较与分析。其中， LG-NLM代表基于特征的NLM去噪方法；BM3D代表去噪优秀的方法；LR-NLM代表改进NLM去噪方法。去噪质量客观评价指标采用峰值信噪比 (peak signal to noise ratio, PSNR)和结构相似性因子 (structural similarity index，SSIM)[15]。

4.1 参数分析

本文改进算法有2个参数需要设置(搜索区域的范围R和图像块大小B)。理想的NLM算法搜索范围R是整个图像区域。由于计算量过大和图像空间相似性的特点，一般都会将搜索范围压缩到中心像素周围一定大小的区域。文献[14]分析了图像搜索范围设置为21像素×21像素可以实现时间效率和去噪性能这2个方面的优化。因此，本文的搜索范围R值为21。

模糊度量相似性是利用图像结构信息获取权重，图像块越大，包含的结构越丰富，但太大后具有相似的图像块较少，导致权重反而会降低。所以，为了得到最优的图像块大小，实验对4幅标准差σ={10,20,40,50}的噪声图像进行以PSNR值为实验评价分析，测试结果如图2所示。

从图2中可以看出，在标准差分别为σ={10,20,40,50}，B={3,5,7,9}时，随着图像块结构信息不断增加，去噪性能具有明显增加。但B={11，13，15},随着图像块增加，PSNR值却又略微减少。分析其原因是模糊度量的视觉特征信息随着图像块的增加，信息量也增加，对去噪也有帮助，但随着图像块过大，图像冗余结构的相似性减少，导致去噪效果反而降低。所以，图像块大小R设置为9将有利于本方法去噪。

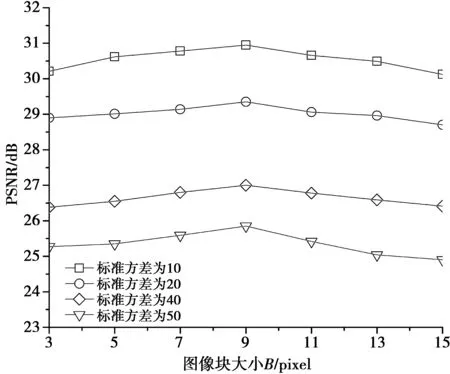
图2 不同图像块在标准差为σ={10,20,40,50}下的PSNR值变化的曲线Fig.2 Value of PSNR curve with different image block under the standard deviation of σ={10,20,40,50}

4.2 去噪性能验证

为了验证算法去噪性能的有效性，从去噪质量客观指标和去噪残差两方面定性分析。本文的算法和LG-NLM均使用Matlab 2015b编程实现，LR-NLM和BM3D源代码来自作者网站。所有比较算法的搜索窗口和图像块大小参考文献[2]分别设置为21像素21像素和9像素9像素。文献[7]分析发现h与噪声方差有近似的线性关系，设置h=0.7×σ。

图3是4种算法分别对σ=40的Lena图帽沿和右眼细节部分的去噪效果图。对比可见，除了LG-NLM，其他几种算法较好地保留图像的结构与细节,但LR-NLM和BM3D算法去噪结果的平滑区域部分不同程度出现轻微的伪影现象。从帽沿的细节信息来看，本文的算法将结构相似性和模糊度量相结合，较好地利用了图像冗余相似性，其边缘区更整齐，图像结构信息保留较完整。

去噪后图像与原始带噪图像, 可以形成一个噪声残差(residual noise, RN)分量[16], RN表示去除的噪声信号部分。由于算法去噪效果不同也会将图像部分信息带到RN分量中，根据图像信息带入的信息量也可以作为一种视觉评价去噪算法的方法。Lean图的去噪残差分量如图4所示，从图4可以看出，LG-NLM和BM3D分别不同程度地将图像整体结构清晰地呈现在RN分量中，说明去噪滤除了很多纹理细节，这些图像的细节信息被保留在噪声残差图像中。本文算法和LR-NLM更好地将图像结构细节信息保留在去噪图像中,噪声残差图像结构信息保留较少，但LR-NLM在平滑区域保留较多地细节。RN图的比较说明了改进算法很好地保持图像边缘和平滑区域良好视觉效果，同时也较好地保留了很多纹理细节部分。改进算法使用模糊度量相似性的方法考虑了图像块中像素间结构相关性,抑制了一部分噪声，保留纹理细节结构较好。

图3 Lena图的4种算法去噪细节比较(σ=40)Fig.3 Detail comparison of four denoising algorithms of image “Lena” with σ=40

图4 Lena图的去噪残差分量图(σ=40)Fig.4 Residual component of image “Lena” with σ=40

图5为图像Man在σ=30下的本文算法与LR-NLM,LG-NLM和BM3D降噪视觉效果图对比。图5a中，LG-NLM对整体细节有一定丢失，有明显的边缘模糊；图5b和图5c能够较好地保留原图像，但过平滑削弱边缘，细节保持能力有限；相对而言，本文算法过渡自然，较完整地保持细节。

图6为图像Barbara的头巾部分在σ=50下，本文算法与LR-NLM,LG-NLM和BM3D降噪视觉效果图对比。头巾纹理细节丰富, LG-NLM和BM3D比LR-NLM保留图像纹理结构更强,本文改进算法更佳地保留纹理细节信息，其图像结构的边缘强度保留更完整。

图5 图像Man的去噪整体效果图比较(σ=30)Fig.5 Overall denoising effect comparison of image “Man” with σ=30

图6 Barbara图像部分细节去噪效果图比较(σ=50)Fig.6 Comparison of denoising effect detail of the part of image “Barbara” with σ=50

分别用PSNR和SSIM 2种评价指标对不同标准方差下的有噪图像用4种算法综合评价，结果如表1和表2所示。

从表1和表2中可以看出，LR-NLM和LG-NLM的整体指标较好，但SSIM值的性能下降较明显。LG-NLM利用特征相似性估计方法，细节难以保留,LR-NLM基于低秩估计相似性方法，去噪效果较好。这2种基于欧式距离的度量方法在噪声较强的情况下，抗干扰能力较弱。对于纹理结构丰富的Barbara和Lena图像，本文算法和BM3D都有较好的去噪效果，但随着噪声强度增加，BM3D性能明显下降，而本文算法保持较好，主要是通过模糊度量的视觉特征可以较好地将图像结构信息提取出来，减少噪声对图像块相似性权重计算的影响。

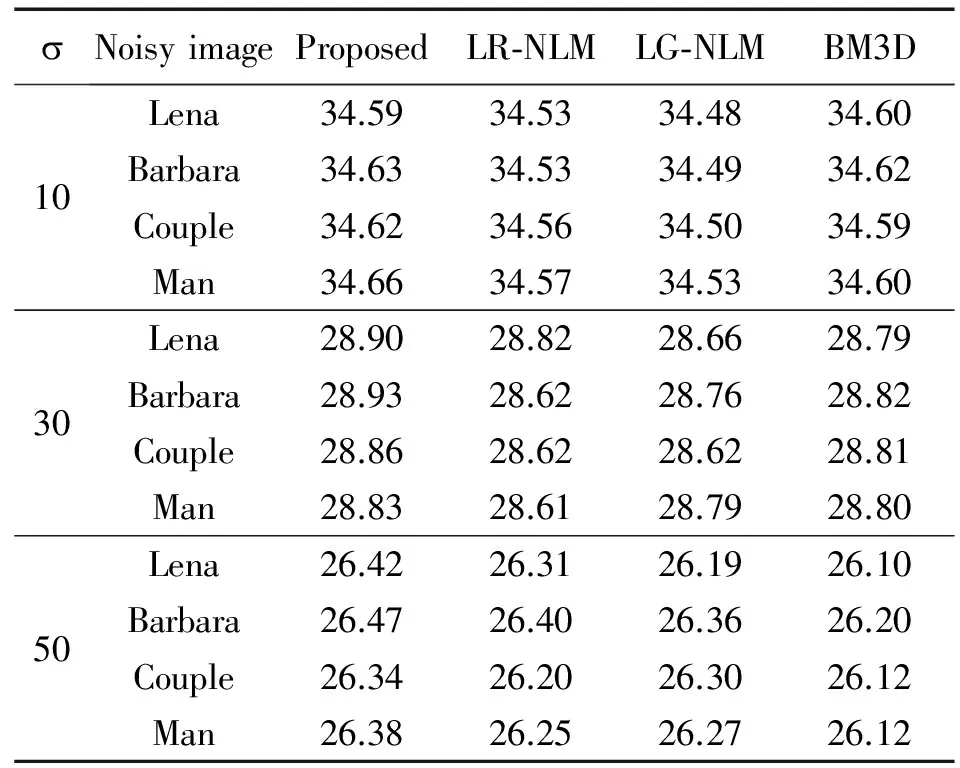
表1 本文算法与LR-NLM,LG-NLM和BM3D在PSNR上的比较Tab.1 Comparison of the algorithm in this paper with LR-NLM, LG-NLM and BM3D in PSNR dB

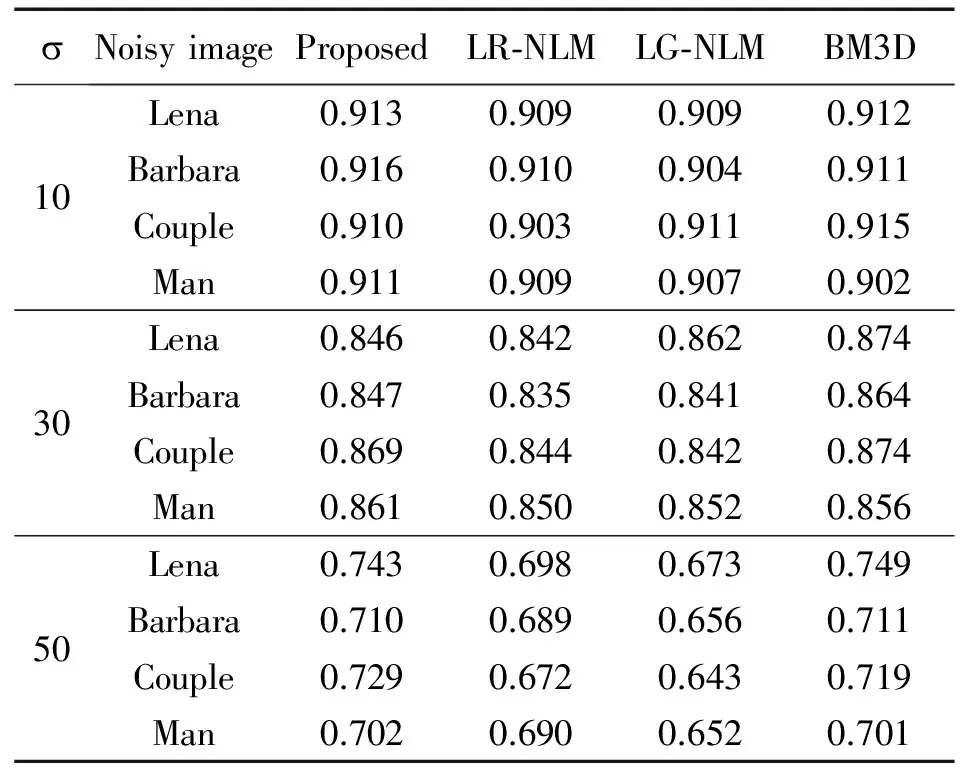
表2 本文算法与LR-NLM,LG-NLM和BM3D在SSIM上的比较Tab.2 Comparison of the algorithm in this paper with LR-NLM, LG-NLM and BM3D in SSIM

对于椒盐噪声的降噪性能方面，比较算法都先采用中值滤波预处理。图7和图8分别为椒盐噪声在噪声密度10%和30%下的多种算法降噪主观视觉对比图。由图7和图8可知，经典的NLM算法对椒盐噪声降噪性能较低，大量噪声无法去除。BM3D与传统的NLM算法相比效果有所提升，但少量椒盐噪声仍然存在．而本文算法和其他2种方法相比，当椒盐噪声密度较低时，降噪效果有显著提升。这是因为本文算法在计算灰度模糊度量和结构模糊度量时，部分椒盐噪声被模糊度量值平滑，起到一定的降噪作用。但随着椒盐噪声密度增加，图像结构被破坏严重，降噪性能都不同程度的降低。

图7 Lena图像在椒盐噪声(10%)下降噪算法视觉对比图Fig.7 Visual contrast of the image “Lena” in salt noise(10%)

图8 Lena图像在椒盐噪声(30%)下降噪算法视觉对比图Fig.8 Visual contrast of the image “Lena” in salt noise(30%)

本文算法，LG-NLM，LR-NLM和BM3D对本文测试的不同大小的4幅图像的平均运行时间如表3所示。测试环境为Dell Inspiron，Core i3，2 GByte内存的笔记本。从表3中看出，对于大小为128像素128像素和256像素256像素的图像，LG-NLM耗时最少，但算法提取特征导致图像细节丢失严重，LR-NLM虽然去噪效果较好，但“低秩估计”操作耗时较大。对于大小为512像素512像素和1 024像素768像素的图像，由于本文的算法以平滑核函数计算模糊度量视觉特征相似性权重能有效地剔除相似性低的图像点，并较好地降低了计算复杂度。该算法计算量增幅较小，与其他几种算法相比，具有良好的加速效果。

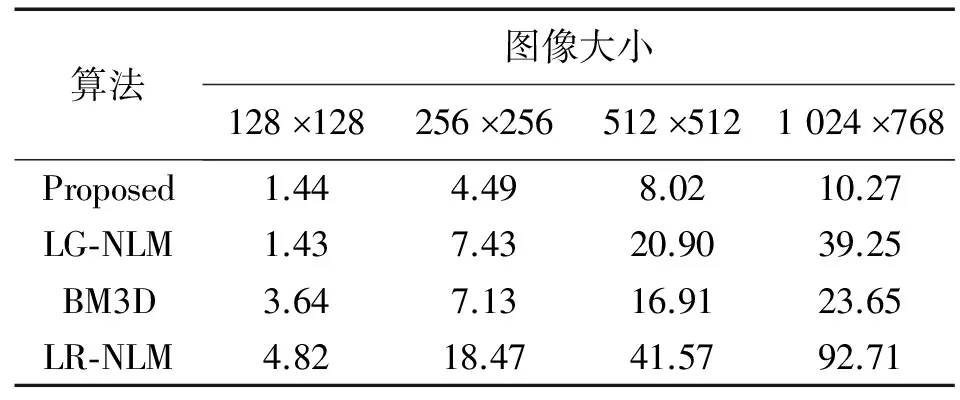
表3 多种算法不同图像大小的平均耗时比较Tab.3 Average time comparison of different image sizes of various algorithms s

5 结 论

针对NLM算法采用欧式距离对图像结构冗余信息利用不够的缺陷，本文提出一种基于模糊度量的改进NLM算法。根据图像空间结构特点，利用模糊度量提取视觉特征，真正做到合理利用结构冗余信息。该方法具有参数设置少，计算量小和易实现的特点。在实验中，本文的算法与当前性能最佳的3种基于图像块去噪算法相比，从PSNR，SSIM 2个指标和视觉效果比较上可知，该方法不仅保留图像细节信息能力强，同时计算效率还有较大的提高。改进的NLM算法对高斯噪声降噪效果接近于图像最优性能，对椒盐噪声也有一定的降噪效果。

参考文献：

[1] MILANFAR P. A Tour of Modern Image Filtering[J]. IEEE Signal Processing Magazine,2013,30(1):106-128.

[2] BUADES A, COLL B, MOREL J M. A review of image denoising algorithms, with a new one[J]. Multiscale Modeling & Simulation, 2005, 4(2): 490-530.

[3] MORILLAS S, GREGORI V, SAPENA A. Fuzzy bilateral filtering for color images[C]//International Conference Image Analysis and Recognition. Berlin Heidelberg：Springer, 2006: 138-145.

[4] DABOV K, FOI A, KATKOVNIK K O, et al. Image denoising by Sparse 3D transform domain collaborayive filtering[J].IEEE Transactions on Image Proscessing, 2007,16(8): 2080-2095.

[5] 罗学刚, 吕俊瑞, 王华军,等. 选择性计算的快速非局部均值图像去噪[J]. 电子科技大学学报, 2015, 44(1):84-90.

LUO Xuegang, LV Junrui, WANG Huajun,et al. Fast Nonlocal Means Image Denoising Algorithm Using Selective Calculation[J]. Journal of University of Electronic Science and Technology of China, 2015, 44 (1):84-90.

[6] 张嵩, 景华炯. 基于Log-Gabor 特征的非局部均值去噪算法及其加速方案研究[J]. 模式识别与人工智能, 2015, 28(003): 266-274.

ZHANG Gao,JING Huajiong.Log-Gabor Feature-Based Nonlocal Means Denoising Algorithm and Its Acceleration Scheme[J]. Pattern Recognition and Artificial Intelligence, 2015, 28(003): 266-274.

[7] 阴盼强,路东明,袁渊.基于马氏距离的改进非局部均值图像去噪算法[J]. 计算机辅助设计与图形学学报, 2016, 28(3):404-410.

YIN Panqiang,LU Dongming,YUAN yuan. An Improved Non-local Means Image De-noising Algorithm Using Mahalanobis Distance[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(3):404-410.

[8] GEORGE A, VEERAMANI P. On some results in fuzzy metric spaces[J]. Fuzzy Sets and Systems，1994，64(3):395-399.

[9] GREGORI V, MORILLAS S, SAPENA A. Examples of fuzzy metrics and applications[J]. Fuzzy Sets and Systems, 2011, 170(1): 95-111.

[10] MORILLAS S, GREGORI V, PERIS F G, et al. A fast impulsive noise color image filter using fuzzy metrics[J]. Real-Time Imaging, 2005, 11(5): 417-428.

[11] JEON G, KANG S H, LEE J K. A robust fuzzy-bilateral filtering method and its application to video deinterlacing[J]. Journal of Real-Time Image Processing, 2016, 11(1):223-233.

[12] GREGORI V, MORILLAS S. Perceptual similarity between color images using fuzzy metrics[J].Journal of Visual Communication and Image Representation, 2016, 34: 230-235.

[13] LI H, SUEN C Y. A novel Non-local means image denoising method based on grey theory[J]. Pattern Recognition, 2016, 49(1): 237-248.

[14] MAY V, KELLER Y, SHARON N, et al. An algorithm for improving Non-Local Means operators via low-rank approximation.[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2016, 25(3):1340-1353.

[15] WANG Z, BOVIK A C, SHEIKH E P. Image quality assessrnent: Formenor Visibility to structural similarity[J].IEEE Transactions on Image Proscessing, 2004, 14(4):600-612.

[16] 焦卫东, 林树森. 用噪声残差似然估计改进经验模态分解基信号去噪方法[J]. 仪器仪表学报, 2014, 35(12): 2808-2816.

JIAO Weidong, LIN Shusen. Improved empirical mode decomposition based signal de-noising approach using likelihood estimation of residual noise[J]. Chinese Journal of Scientific Instrument, 2014, 35(12): 2808-2816.