动态随机有效停车泊位预测方法*

段满珍，陈 光，张 林，米雪玉

(华北理工大学 建筑工程学院，河北 唐山 063009)

有效停车泊位是指开放停车场内未被占用的停车位，有效泊位数多少是驾驶员停车选择的重要依据。受工作、生活等作息习惯影响，停车场泊位利用情况具有一定的宏观规律性，但同时又受停车场位置、泊位类型、收费标准、气候变化、周边交通条件等多种因素的干扰。因而，停车泊位利用具有复杂性和随机性特点，导致停车场的有效泊位变化呈现明显的动态随机性[1]。随着城市交通问题日益严重[2]和驾驶员对有效停车泊位信息需求的增加，动态随机有效泊位预测成为智能停车诱导系统的重要组成部分[3]。

传统有效泊位预测中，主要采用影响因素分析法和一维时间序列法[4]，但只能实现短时预测，精度较低。一些学者开始将神经网络技术引入有效泊位的预测中，但早期模糊神经网络方法只能输出模糊化程度较高的“空，满”信息[5]，仍不能实现对泊位信息的准确预测。而单一网络技术或静态BP网络预测方法[6]，则存在对网络输入维数和神经元个数等参数选取随机性的弊端，或缺乏对动态系统多维特性的考虑也无法实现对动态泊位的有效预测。近几年随着混沌理论和动态神经网络融合技术的发展，尤其是在气候预测[7]、用电负荷[8]、太阳直接日射逐日曝辐量[9]以及基坑变形量[10]等领域的成功应用，为动态随机泊位预测提供了崭新思路。但由于混沌相空间嵌入维数和延迟时间等参数的求解方法对预测结果的精度影响较大[7]，若对停车泊位数据处理方法选用中缺乏对其非线性特性考虑，也会导致预测结果准确性较差，例如基于时间序列线性假设的自相关法[11]的应用。

针对以上情况，尤其是考虑个性化停车诱导[12]条件下驾驶员对动态泊位需求预测需要，避免静态神经网络技术和线性求解方法不足，利用混沌相空间理论C-C算法在求解非线性关系模型方面的优势，笔者研究了基于C-C算法和网络融合技术的动态随机有效泊位预测方法，并重点对技术融合过程和算法进行研究，利用实测数据进行模型仿真实验分析。目的在于实现动态随机泊位信息的准确预测，为驾驶员提供有效地动态泊位信息，减少寻泊交通流，同时避免群体式诱导方式带来的局部停车拥堵，减缓交通压力。

1 理论基础

1.1 C-C算法

C-C算法融合了相空间理论自相关函数和互信息方法的优点，在有效减少计算量基础上又能保持系统的非线性特征。

对一个时间序列重构后的相空间X，其关联积分定义如式(1)[13-14]：

(1)

式中：N为数据集合的长度；τ为时间尺度；r为半径；M=N-(m-1)τ为m维嵌入后的点数。

C-C算法的研究与函数S(m，N，r，t)=C(m，N，r，t)-Cm(1，N，r，t)的值有关。由于时间序列长度N有限，半径r也不可能无限小，通常可用一个线性区域的斜率来近似表示关联维，如式(2)：

(2)

为研究时间序列的动力学特性，找到合适的延迟时间，需将整个时间序列S(m，N，r，t)=C(m，N，r，t)-Cm(1，N，r，t)分为τ个子序列，如式(3)：

(3)

当N→∞时，有式(4)：

(4)

选择最大和最小半径r，定义其差量如式(5)：

ΔS(m，τ)=max{S(m，rj，τ，N)}-min{S(m，rj，τ，N)}

(5)

根据统计结论，取m=2，3，4，5；rj=iσ/2。其中：i=1，2，3，4。

(6)

(7)

(8)

1.2 小数据法判定数据的非线性特性

对停车数据时间序列进行相空间重构的基础上，进一步分析其特性。

根据m和τ的结果重构相空间，形式如下：Y(t)={x(t)，x(t+τ)，x(t+2τ)，...，x(t+(m-1)τ)}。其中：t=1，2，…，[N-(m-1)τ] ，Y(t)为相空间中的点。

根据M.T.ROSENSTEIN的结论[16]，小数据量法具有较好地鲁棒性，对嵌入维数和时延参数选取不具敏感特性。笔者同样选取小数据量法来验证重构后的相空间是否具有混沌特性。

首先，搜寻重构轨道上每个点对应的最近邻点，如式(9)：

(9)

式中：p为时间序列的平均周期；Y(t)为相空间中的点；dT(0)为初始时刻一对最近邻点的距离。

通过轨道上每个最近邻近点平均发散率进行最大 Lyapunov 指数估算，如式(10)：

(10)

式中：Δt为样本0周期；dT(i)为基本轨道上第t对最近邻近点经过i个离散时间步长的距离；若λ=0，表示系统出现周期现象；若λ>0，系统具有混沌特征；若λ<0，系统有稳定不动点。

2 C-C算法与Elman网络技术融合

基于动态随机有效泊位的非线性特性，笔者选用适合于非线性关系的C-C算法来求解随机泊位混沌相空间的嵌入维数m和延迟时间τ值，并将其与动态网络技术融合，联合进行动态随机泊位的预测，更能真实地反映随机泊位变化的非线性特性。

为实现动态随机泊位的准确预测，参照递归网络技术在其他领域的研究结果[7，17]，笔者选用Elman递归神经网络。Elman网络是一种动态递归神经网络，该网络的特点是：隐含层输出值通过承接层存储和延迟，将中间结果自联到隐含层输入中，这种自联使其保留了对历史数据的敏感性和传递性，通过自身网络互联增加了网络对数据处理的动态性，从而达到了动态建模目的，能更生动、更真实地反映系统动态特性。

Elman递归神经网络的结构如图1。

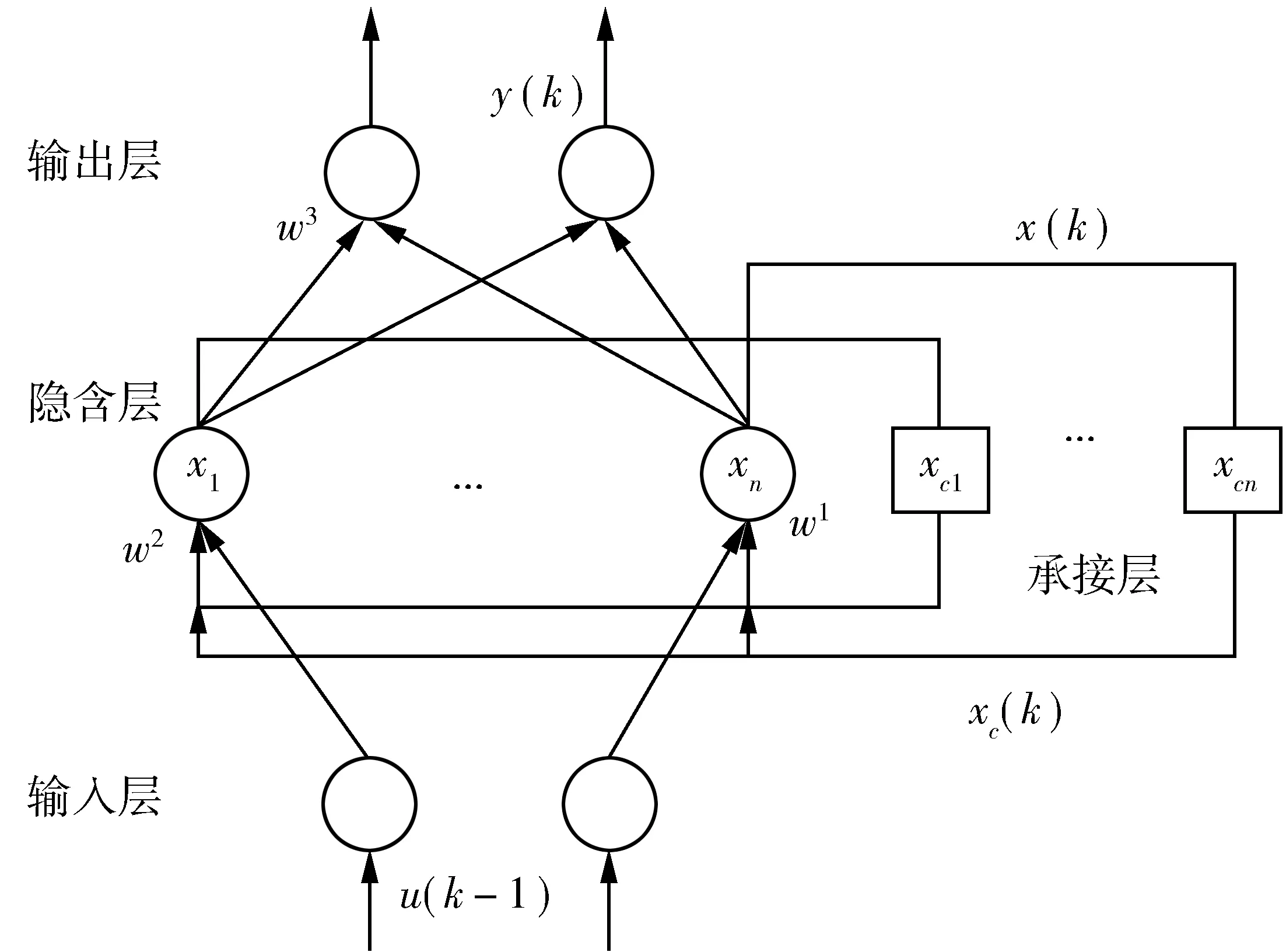
图1 Elman网络结构示意Fig. 1 Elman neural network structure diagram

Elman网络的非线性空间表达如式(11)：

(11)

C-C算法与Elman递归网络融合，主要是为避免递归网络模型参数输入的随机性。融合思想是：将C-C算法得到的相空间参数延迟时间τ和嵌入维数m作为递归网络输入的依据。

例如：将网络输入向量u的取值设为m维重构相空间的向量；中间层输出向量x和承接层输出向量xc为n维，取值为2m+1[10]；输出向量y为P维，其取决于模型输出变量个数，文中输出变量只有动态预测泊位数，因此P=1；w3，w2，w1分别表示中间层到输出层、输入层到中间层、承接层到中间层的连接权值；f(·)为中间层神经元的传递函数，文中采用S函数；g(·)为输出神经元的传递函数，为中间层输出的线性组合。

3 动态泊位预测模型构建及算法

3.1 C-C算法与递归网络融合的预测模型

根据上述融合思想，设计动态随机泊位预测的递归神经网络模型参数。其中：网络输入维数u等于嵌入维数m；每个输入数据之间的时间间隔取值为τ，即将x(t)，x(t+τ)，x(t+2τ)，…，x[t+(m-1)τ)] 时间序列作为网络学习样本输入；递归网络的隐含层取单层；神经元个数n=2m+1，承接层单元数目与隐含层神经元数目相同；输出层含有一个神经元—动态随机有效泊位数：x[t+1+(m-1)τ)]。

网络输入、输出模型如式(12)、(13)。

(12)

(13)

递归网络隐含层传递函数为tansig，输出层线性传递函数为purelin。其中：tansig为S型正切函数，purelin为纯线性函数。隐含层输出函数表示为：x(k)=tansig[Wax(k-1)+Wbu(k-1)+b1] ，输出层输出函数为：y(k)=purelin[Wcx(k)+b2]。

3.2 预测模型算法设计

融合后的预测模型求解步骤如下：

第1步：收集停车场有效泊位变化的历史数据，按时间序列要求进行整理，假设整理后的时间序列为：{x(t)|t=1，2，…，N}；

第2步：利用C-C算法计算嵌入维数m和最优延迟时间τ；

第3步：利用求取的最小嵌入维数m和最优时延参数τ对原时间序列进行相空间重构，得到新的相空间矢量：Y(t)={x(t)，x(t+τ)，x(t+2τ)，…，x[t+(m-1)τ]}，t=1，2，…，[N-(m-1)τ]。并采用小数据法判断其是否具有混沌特性；

第4步：利用第3步得到的m和τ值，构建基于C-C算法的Elman神经网络预测模型；

第5步：根据预测需要，设定网络训练误差。结合样本数据情况，选取适量的训练样本(其余为目标样本)，进行模型网络训练，当达到误差要求时，进入第6步；若测试误差较大，重新进行网络训练，或重新设计网络结构。

第6步：选取预测时间点和预测样本，进行模型预测。

4 模型仿真与结果分析

4.1 数据采集

根据医院停车数据周期性差异[18]，分别从唐山市工人医院两个工作日调查数据中截取08：00—17：00车辆停放数据(表1)，统计时间间隔为10 min。停车数据整理后得到有效泊位数据(图2)。图2中：纵坐标正数为有效空闲泊位，负数为停车溢出，既非规划空间有停车或有车辆排队造成的溢出。

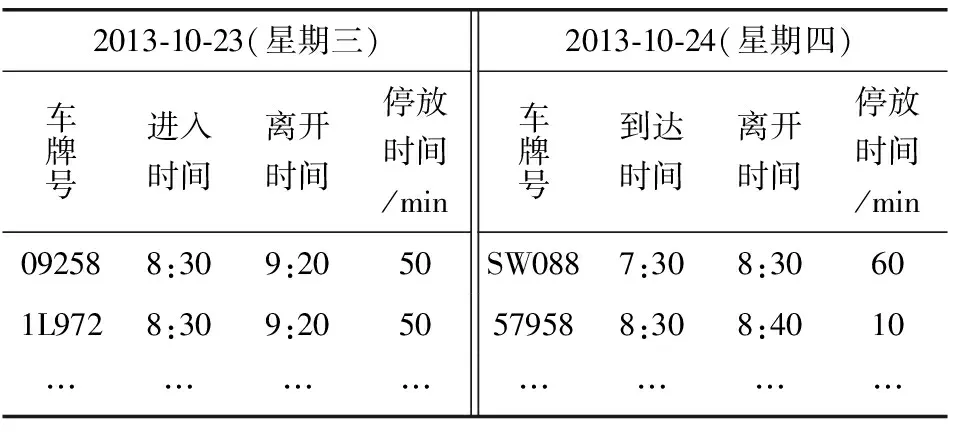
表1 医院停车数据Table 1 Data of parking vehicles in hospital

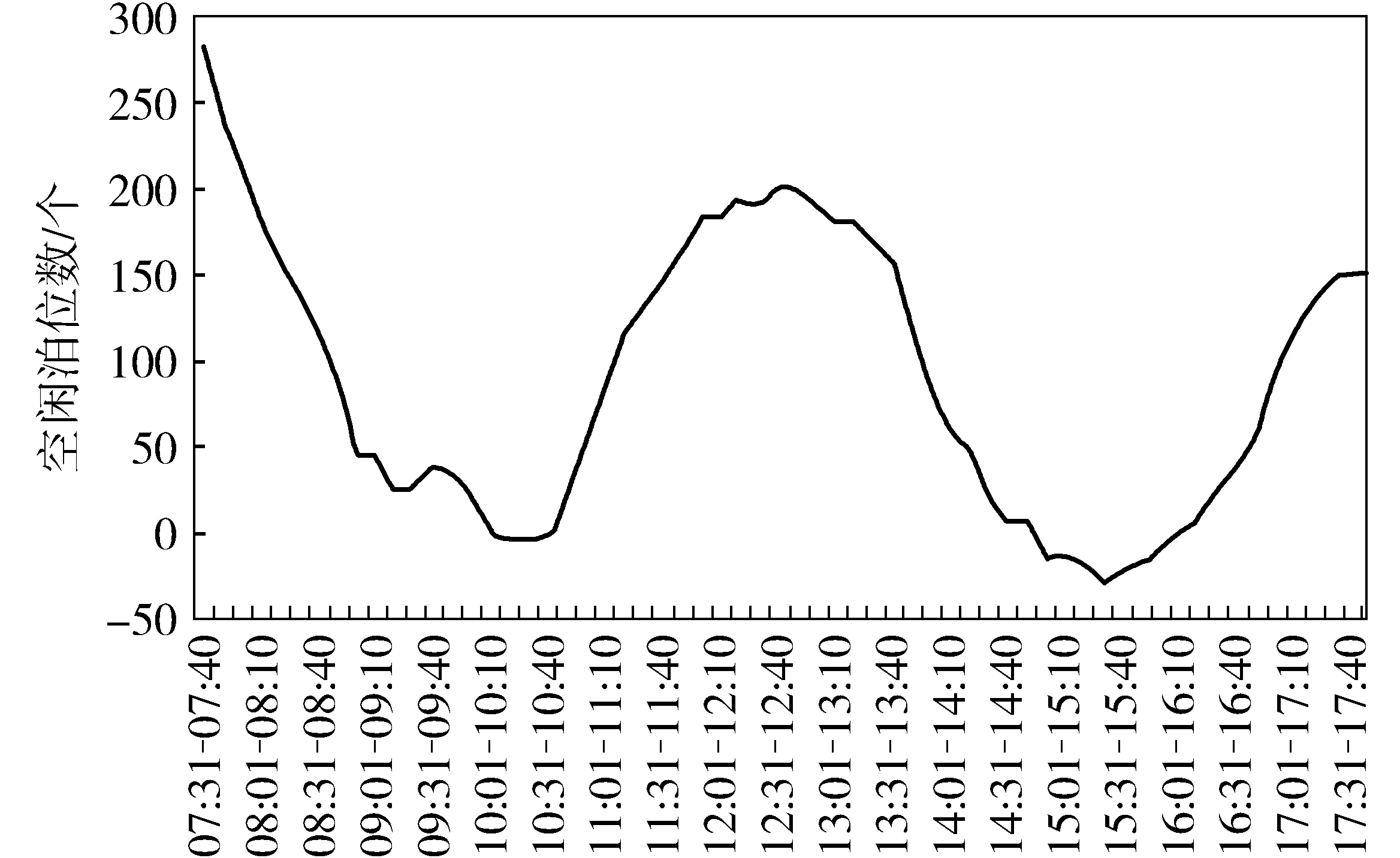
图2 医院某日的停车场空闲泊位时序Fig. 2 Timing diagram of unoccupied spaces in parking lot

4.2 利用C-C算法进行模型参数计算

设计C-C算法，导入停车数据，利用MATLAB计算，其结果如图3。

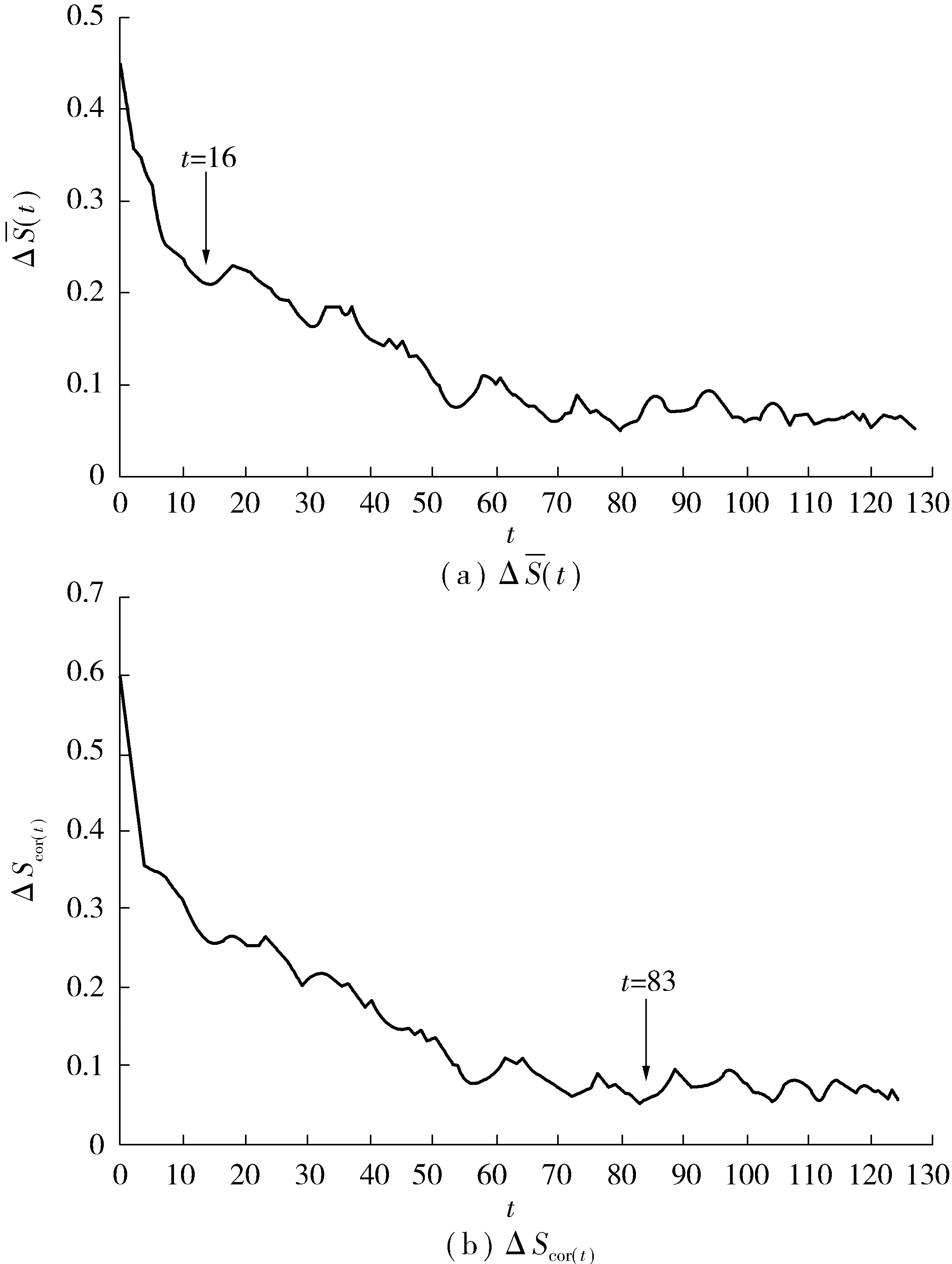
图3 停车变化曲线Fig. 3 Parking data curve

4.3 停车数据模型混沌特性判定

根据C-C算法得到的m和τ值，重构相空间为：Y(t)={x(t)，x(t+8)，x(t+16)}。采用小数据量法计算最大Lyapunov指数，得到K1=0.357 1，证明重构动态随机泊位系统仍然具有混沌特性。

4.4 动态泊位预测模型构建

利用唐山市工人医院停车场泊位变化的108组数据，进行间隔时间为10 min的短时空闲泊位预测分析。

网络训练样本选择：采用前15 h(90组数据)的泊位变化数据作为网络训练样本，后3 h(18组数据)的泊位变化数据作为网络测试数据。网络训练每4 h的泊位变化数据作为输入向量，第5 h泊位数据作为目标向量，为提高模型的预测精度，网络训练前先将采集数据进行预处理，去除明显有错误的数据，再采用MATLAB的Premnmx函数进行数据归一化处理。MATLAB语句为：[pn，minp，maxp，tn，mint，maxt]= Premnmx(p，t)。

4.4.1 C-C算法与网络模型的融合

根据融合算法思想，利用C-C算法计算，并将结果设计预测模型输入参数。其中：嵌入维数6作为泊位预测模型的输入层神经元个数，则隐含层神经元个数n=7；每个神经元之间的时间间隔等于延迟时间，取值为8；输出层神经元个数为1，即下一个10 min动态泊位预测值。

构建Elman网络的MATLAB语句为：net=newelm(minmax(pn)，[71]，{‘tansig’，’purelin’})；网络最大训练次数为：net.trainparam.epochs=2000；网络训练目标误差为：net.trainparam.goal=0.01。

4.4.2 仿真结果分析

当网络训练次数474次时达到预设目标误差，运行停止，训练误差曲线如图4。利用训练好的网络进行预测，数据模型输出拟合效果如图5。由图5看出：模型输出值与实测值一致性较好。

图4 网络训练误差曲线Fig. 4 Network training error curve

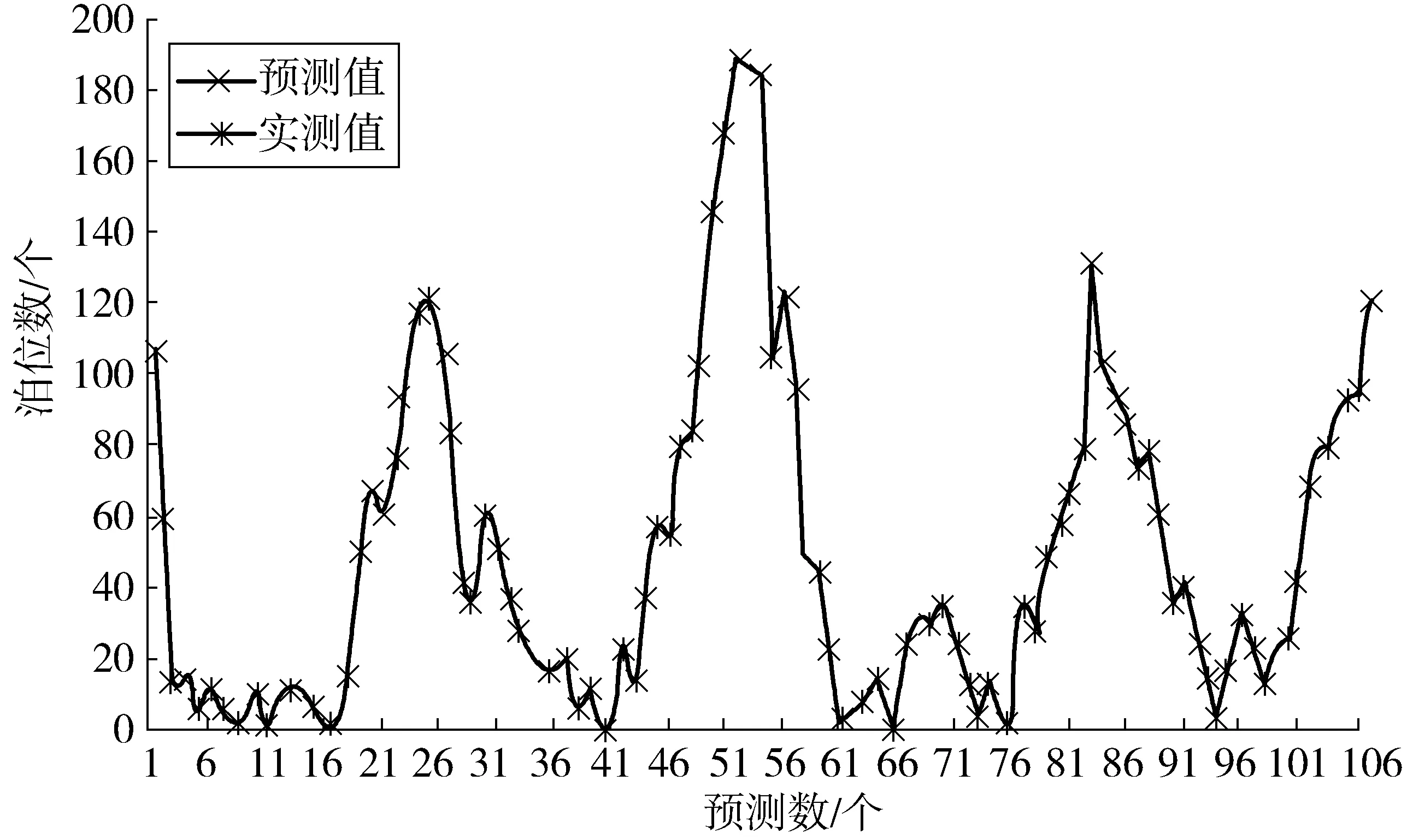
图5 模型实测值和输出值比较Fig. 5 Comparison of measured values and outputs

图6为空闲泊位预测误差。图6(a)平均绝对误差为0.897 2个；图6(b)输出值平均相对误差为1.434%，最大相对误差8.33%。明显优于文献[11] 中采用自相关函数法得到的平均相对误差2.13%，平均绝对误差为1.808 9个，最大相对误差11.61%的预测结果，这说明采用非线性C-C算法与递归网络融合后能达到更准确地预测效果。表明在动态随机泊位预测建模中，将相空间C-C算法与Elman网络融合方法是比较成功的。

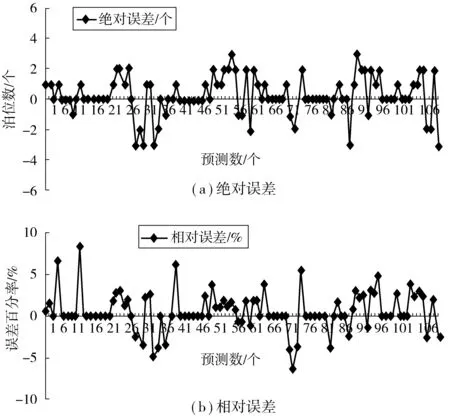
图6 空闲泊位预测误差Fig. 6 Error of free parking space prediction

实验结果表明：基于C-C算法与Elman网络融合模型预测结果拟合效果较好，预测精度较高。利用该方法对其他停车场停车泊位预测也得到相近的结果，说明该方法可较好地实现随机停车泊位建模和动态预测。

5 结 论

针对现有停车需求预测方法难以实现动态随机条件下对泊位状态变化的精准预测，不能为驾驶员提供个性化停车诱导服务的问题，笔者对动态随机条件下停车泊位需求预测方法进行了研究。混沌理论研究成果表明：C-C算法能较好地从系统参与动态变化的全部时间序列中提取系统长期演化的内部信息，揭示动态泊位变化系统随机现象的混沌特征和复杂规律。同时，由于Elman网络通过自联方式可保留对历史数据的敏感性和传递性。因此，利用Elman递归网络建模可较好解决一般网络不能解决的非线性复杂问题，达到动态建模、真实反应系统动态特征的目的。

将C-C算法和Elman网络技术融合，重构相空间时间序列作为网络学习输入样本，嵌入维数作为神经元个数选择依据，用于动态随机有效泊位实时预测，既能有效挖掘动态随机停车系统时间序列隐含的内部信息，充分揭示停车泊位预测系统复杂的运动规律，又能避免单一网络模型预测输入变量和参数选择的盲目性。

仿真实验结果表明：基于C-C算法与Elman网络融合的动态停车泊位预测模型相比于其他预测方法，其最大相对误差、平均相对误差和平均绝对误差等都明显降低，说明二者融合是实现动态随机泊位预测的有效方法。

参考文献(References)：

[1] 李志纯，黄海军.拟动态随机停车行为模型及可靠度分析[M]//可持续发展的中国交通——2005全国博士生学术论坛(交通运输工程学科)论文集(上册).北京：北京交通大学出版社，2005：218-228.

LI Zhichun，HUANG Haijun.AQuasi-DynamicStochasticParkingModelAndReliabilityAnalysis[M]//Sustainable Development of China’s Transportation—The 2005 National Doctoral Academic Forum (Transportation Engineering)(1).Beijing：Beijing Jiaotong University Press，2005：218-228.

[2] 段满珍，轧红颖，李珊珊，等.震害道路通行能力评估模型[J].重庆交通大学学报(自然科学版)，2017，36(5)：79-85.

DUAN Manzhen，YA Hongying，LI Shanshan，et al.Assessment model for traffic capacity after seismic disaster[J].JournalofChongqingJiaotongUniversity(NaturalScience)，2017，36(5)：79-85.

[3] 段满珍，杨兆升，米雪玉，等.基于居住区共享停车的双层规划诱导模型[J].西南交通大学学报，2016，51(6)：1250-1257.

DUAN Manzhen，YANG Zhaosheng，MI Xueyu，et al.Bi-level programming model for shared parking considering residential parking resources[J].JournalofSouthwestJiaotongUniversity，2016，51(6)：1250-1257.

[4] 段满珍，陈光，米雪玉，等.居住区停车泊位需求预测二步骤法[J].重庆交通大学学报(自然科学版)，2016，35(1)：152-155.

DUAN Manzhen，CHEN Guang，MI Xueyu，et al.Two steps method of parking demand forecast at residential area[J].JournalofChongqingJiaotongUniversity(NaturalScience)，2016，35(1)：152-155.

[5] 杨兆升，陈晓冬.智能化停车诱导系统有效停车泊位数据的预测技术研究[J].交通运输系统工程与信息，2003，3(4)：12.

YANG Zhaosheng，CHEN Xiaodong.Research on the estimation for effective parking space of the intelligentized parking guidance system[J].JournalofTransportationSystemsEngineeringandInformationTechnology，2003，3(4)：12.

[6] 何洪波，韩印，姚佼.基于混沌和BP神经网络的有效停车泊位预测[J].交通与运输，2012(7)：24-28.

HE Hongbo，HAN Yin，YAO Jiao.The prediction of effective parking space based on chaos and BP neural network[J].TrafficandTransportation，2012(7)：24-28.

[7] 董兆俊，滕军，王骥鹏.基于相空间重构与模糊神经网络耦合的海温预测模型[J].热带海洋学报，2008，27(4)：73-76.

DONG Zhaojun，TENG Jun，WANG Jipeng.Application of phase space reconstruction and ANFIS model in SST forecasting[J].JournalofTropicalOceanography，2008，27(4)：73-76.

[8] 张智晟，孙雅明，何云鹏.基于相空间重构理论和优化递归神经网络结合的短期负荷预测方法[J].中国电力，2004，37(1)：19-23.

ZHANG Zhisheng，SUN Yaming，HE Yunpeng.A new approach of STLF based on combination of phase space reconstruction theory and optimal recursive neural networks[J].ElectricPower，2004，37(1)：19-23.

[9] 谢云林.基于相空间重构小波神经网络的太阳直接日射逐日曝辐量预测[D].合肥：合肥工业大学，2012.

XIE Yunlin.DailyDirectSolarRadiationExposurePredictionBasedonPhaseSpaceReconstructionofWaveletNeuralNetwork[D].Hefei：Hefei University of Technology，2012.

[10] 赵启嘉.基于动态递归神经网络及相空间重构理论的深基坑工程变形预测研究[D].上海：同济大学，2008.

ZHAO Qijia.ResearchonDeformationPredictionofDeepExcavationbyRecurrentNeuralNetworkandPhaseSpaceReconstruction[D].Shanghai：Tongji University，2008.

[11] 陈群，晏克非，王仁涛，等.基于相空间重构及Elman网络的停车泊位数据预测[J].同济大学学报(自然科学版)，2007，35(5)：607-611.

CHEN Qun，YAN Kefei，WANG Rentao et al.Parking space information prediction based on phrase construction and elman neural network[J].JournalofTongjiUniversity(NaturalScience)，2007，35(5)：607-611.

[12] 段满珍，杨兆升，张林，等.个性化诱导下的居住区共享停车泊位分配模型[J].东北大学学报(自然科学版)，2017，38(2)：174-179.

DUAN Manzhen，YANG Zhaosheng，ZHANG Lin，et al.Parking spaces allocation model of the residential areas sharing parking base on personalized guidance[J].JournalofNortheasternUniversity(NaturalScience)，2017，38(2)：174-179.

[13] KUGIUMTZIS D.State space reconstruction parameters in the analysis of chaotic time series—the role of the time window length[J].PhysicaD：NonlinearPhenomena，1996，95(1)：13-28.

[14] SPROTT J C.Automatic generation of strange attractors[J].Computers&Graphics，1993，17(3)：325-332.

[15] KIM H S，EYKHOLT R，SALAS J D.Nonlinear dynamics delay times，and embedding windows[J].PhysicaD：NonlinearPhenomena，1999，127(1/2)：48-60.

[16] ROSENSTEIN M T，COLLINS J J，LUCA C J D.A practical method for calculating largest Lyapunov exponents from small data sets[J].PhysicaD：NonlinearPhenomena，1993，65(1/2)：117-134.

[17] 董春娇，邵春福，熊志华，等.基于Elman神经网络的道路网短时交通流预测方法[J].交通运输系统工程与信息，2010，10(1)：145-151.

DONG Chunjiao，SHAO Chunfu，XIONG Zhihua，et al.Short-term traffic flow forecasting of road network based on Elman neural network[J].JournalofTransportationSystemsEngineeringandInformationTechnology，2010，10(1)：145-151.

[18] 段满珍，杨兆升，张林，等.居住区泊位对外共享能力评估模型[J].交通运输系统工程与信息，2015，15(4)：106-112.

DUAN Manzhen，YANG Zhaosheng，ZHANG Lin，et al.Residential parking spaces shared capability assessment model[J].JournalofTransportationSystemsEngineeringandInformationTechnology，2015，15(4)：106-117.

[19] 张雨，任成龙.确定重构相空间维数的方法[J].国防科技大学学报，2005，27(6)：101-105.

ZHANG Yu，REN Chenglong.The methods to confirm the dimension of re-constructed phase space[J].JournalofNationalUniversityofDefenseTechnology，2005，27(6)：101-105.