基于朴素贝叶斯轨道交通网络客流分配模型*

翁小雄，汪周盼，黄靖翔

(华南理工大学 土木与交通学院，广东 广州 510641)

0 引 言

轨道交通网络客流分配比例是多路径费率清分的基础。同时，客流作为网络化运营基础，其大小和分布特征是合理制定网络运营计划、提高各线路运营协调性、发挥系统的整体能力和综合效益的关键[1]。目前，国内外学者对轨道交通网络研究比较深入[2-3]，但对城市轨道交通网络客流分配研究较少。传统求取轨道交通客流分配比例方法通常是基于时间或者路程的阻抗函数，常见的有：正态函数模型[1]以及Logit模型[4]，通常需要人工对该模型中的参数进行调查标定，数据来源的不确定性导致参数误差较大，模型求解结果准确性更难以保证。

目前，国内轨道交通网络均已经实现自动售检票系统(auto fare collection，AFC)来记录乘客的出行信息。该系统能准确记录乘客进出站地点和时间，国内外也有一些学者通过AFC数据来进行轨道交通网络及客流分析。ZHOU Feng等[5]利用AFC数据中的进出站时间和列车发车计划表，通过算法计算了客流在不同路径比例，但并未对AFC数据充分利用；SUN Yanshuo等[6]通过对AFC数据可靠性进行调查，重点分析了行程时间准确性，以此来估计乘客路径选择行为，但需要人工调查每个站点的进出站时间，工作量巨大，且调查数据准确性有待考量；SI Bingfeng等[7]建立了基于行程时间以及换乘成本阻抗的Logit清分模型，并通过改进的Logit模型解决网络客流分配问题，形式依然是阻抗函数，并未对AFC数据深入研究。此外，也有学者利用AFC数据进行了其他方面研究，C.JOANNE[8]利用AFC数据对出行OD矩阵以及行程时间进行了分析；T.KUSAKABE等[9-10]利用智能卡数据分析了乘客列车班次的选择行为；MA Xiaolei等[11]利用AFC数据挖掘了乘客上车站点信息；WANG Ya等[12]利用AFC数据，基于出行模式识别，推测了每个乘客的出行链信息；贝叶斯在轨道交通应用方面，朱顺应等[13]利用该模型进行乘客满意度分析。

笔者在分析轨道交通乘客行程时间构成基础上，利用乘客AFC刷卡数据，并结合朴素贝叶斯分类器，提出了新的轨道交通网络客流分配模型，为城市轨道交通费率清分问题提出新的解决思路。

1 行程时间组成要素

1.1 行程时间构成

乘客乘坐轨道交通出行的行程时间主要包含以下组成要素：① 进站闸机到站台的步行时间tew；② 起始站点候车时间tw；③ 乘车时间tr；④ 换乘站点步行时间ttwalk；⑤ 换乘站点候车时间ttwaite；⑥ 出站步行时间tow。其中：ttwalk和ttwaite仅在出行换乘时存在。

根据石俊刚等[13]研究表明，乘客行程时间各部分构成相互独立，且在满足一定假设条件前提下，有如下结论：

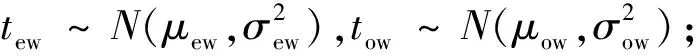
2) 由于起始站点候车时间是一个与列车发车间隔有关的量，且介于0到发车间隔H之间。故可认为乘客进站候车时间tw服从均匀分布，即：tw～U[0，H] ；

3) 当假定列车都按照运行计划表运行，则可认为乘客乘车时间tr为常量；

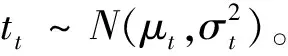
(1)

(2)

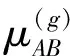
1.2 行程时间参数

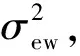
1.2.1 进出站步行时间参数

表1为AFC数据结构。表1中：可以获得乘客在某一OD对上的行程时间，tAB=tout-tin。其中：tout和tin分别为出站时间和进站时间；tAB为该OD对上的行程时间。

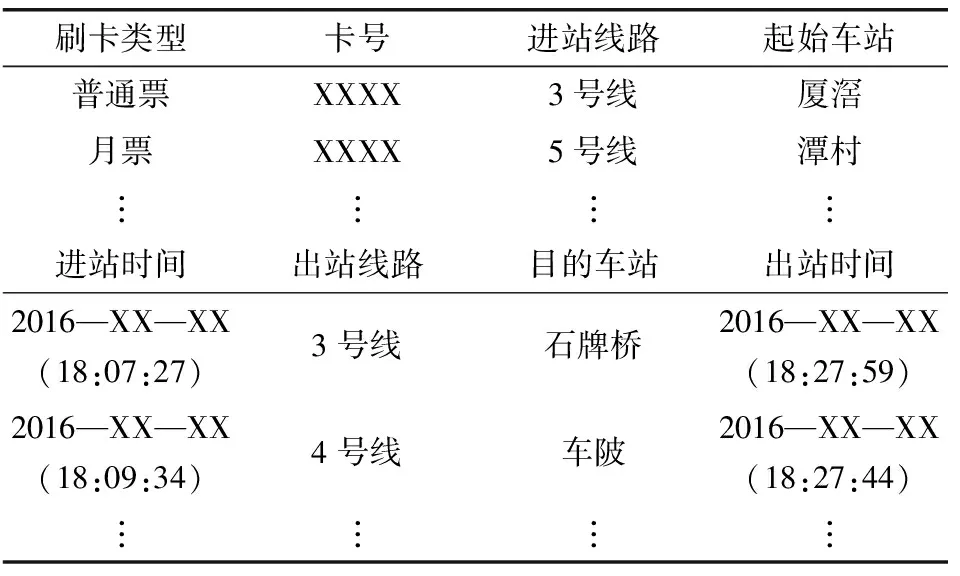
表1 AFC数据结构Table 1 AFC data structure

对进出站步行时间的参数估计如下：

1) 以单路径无换乘OD为对象，其中起始站为A，目的站为B；为OD的行程时间为tAB；此时乘客的行程时间仅由tew、tw、tr、tow构成。则路径行程时间的均值和方差如式(3)、(4)：

(3)

(4)

2) 根据已知乘客AFC数据，为保证参数估计的准确性，要求估计过程中客流样本尽量大，即找出OD间客流量最大的车站；并对该车站进站和出站时间进行人工调查，并采用矩估计获取相应的进站和出站时间均值μ和σ；

3) 已知tr、HA和某个车站进出站时间的μ和σ，并结合式(3)、(4)，即可推断出其他车站进出站步行时间参数。

1.2.2 换乘时间参数

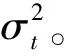
换乘步行时间参数估计步骤为：

1) 选取某一单路径仅换乘一次OD为对象，起始站为A，目的站为B，则该路径行程时间的均值和方差如式(5)、(6)：

(5)

(6)

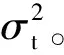
2 轨道交通网络客流分配模型

2.1 朴素贝叶斯算法

朴素贝叶斯算法是一种概率分类器，旨在使用概率表示各种事件的不确定性，且假设属性之间相互独立，是贝叶斯算法中使用最广泛的一种算法。朴素贝叶斯分类的基本思想为[7]：

1) 每个数据样本用n维特征向量X={x1，x2，…，xn}表示，分别描述该样本n个特征属性A1，A2，…，An的度量。

2) 假定有m个类C1，C2，…，Cm；给定一个分类标号未知的数据样本X，分类器将预测X属于具有最高后验概率的类，即朴素贝叶斯分类将未知的样本X分配给Ci(i=1，2，…，m)，当且仅当P(Ci|X)>P(Cj|X)，对任意的j=1，2，…，m(j≠i)；其中：P(Ci|X)最大的类称为最大后验假定。

根据贝叶斯定理，最大后验假定按式(7)计算：

(7)

式中：P(Ci)为先验概率，若Ci类的先验概率未知，则通常假定这些类是等概率的，即P(C1)=P(C2)=…=P(Cm)，对所有的类别来说P(X)相同。

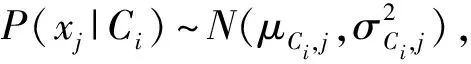
(8)

3) 判定未知样本X的分类，对每个类别分别计算后验概率P(Ci|X)，当且仅当P(Ci|X)>P(Cj|X)对于任意的i，j∈{1，2，…，m}均成立，则有样本X属于Ci类。

2.2 客流分配模型

2.2.1 算法构思

基于乘客刷卡AFC数据，可将乘客进出站时间的差值，即行程时间作为一个特征属性，且该属性为一个连续属性；其次，假设OD间的有k条路径，每条路径可认为是一个类别，即有k类，且每个类别的先验概率均为1/k；再次，由AFC数据计算的OD间各路径行程时间均值和方差，可作为所有已知样本行程时间属性的均值和方差。每个乘客AFC数据可作为一个样本，估算每个样本属于每条有效路径的后验概率，并将其划入后验概率最大的路径。

2.2.2 算法设计

以多路径OD为对象，起始站点为A，目的站为B，OD间存在k条有效路径。根据分析可知，特征属性为行程时间，每条路径的先验概率为1/k；该OD间每名乘客AFC数据作为一个样本。

1) 根据式(1)、(2)计算每条路径行程时间的均值和方差。

2) 计算每个样本，即每名乘客在每条路径的后验概率，由于行程时间为连续属性，其计算如式(9)：

(9)

式中：tAB为每个样本行程时间；Ci为不同路径。

3) 比较该样本在每条路径后验概率P(Ci|X)大小，则每个样本的类标记λ(Ci)如式(10)：

λ(Ci)=argmaxP(Ci|Χ)

(10)

3 算例验证

笔者以图1中的广州地铁线路为背景，起始站点为市二宫，终点站点为东山口的OD作为研究对象。由图1可知：该OD存在2条有效路径。

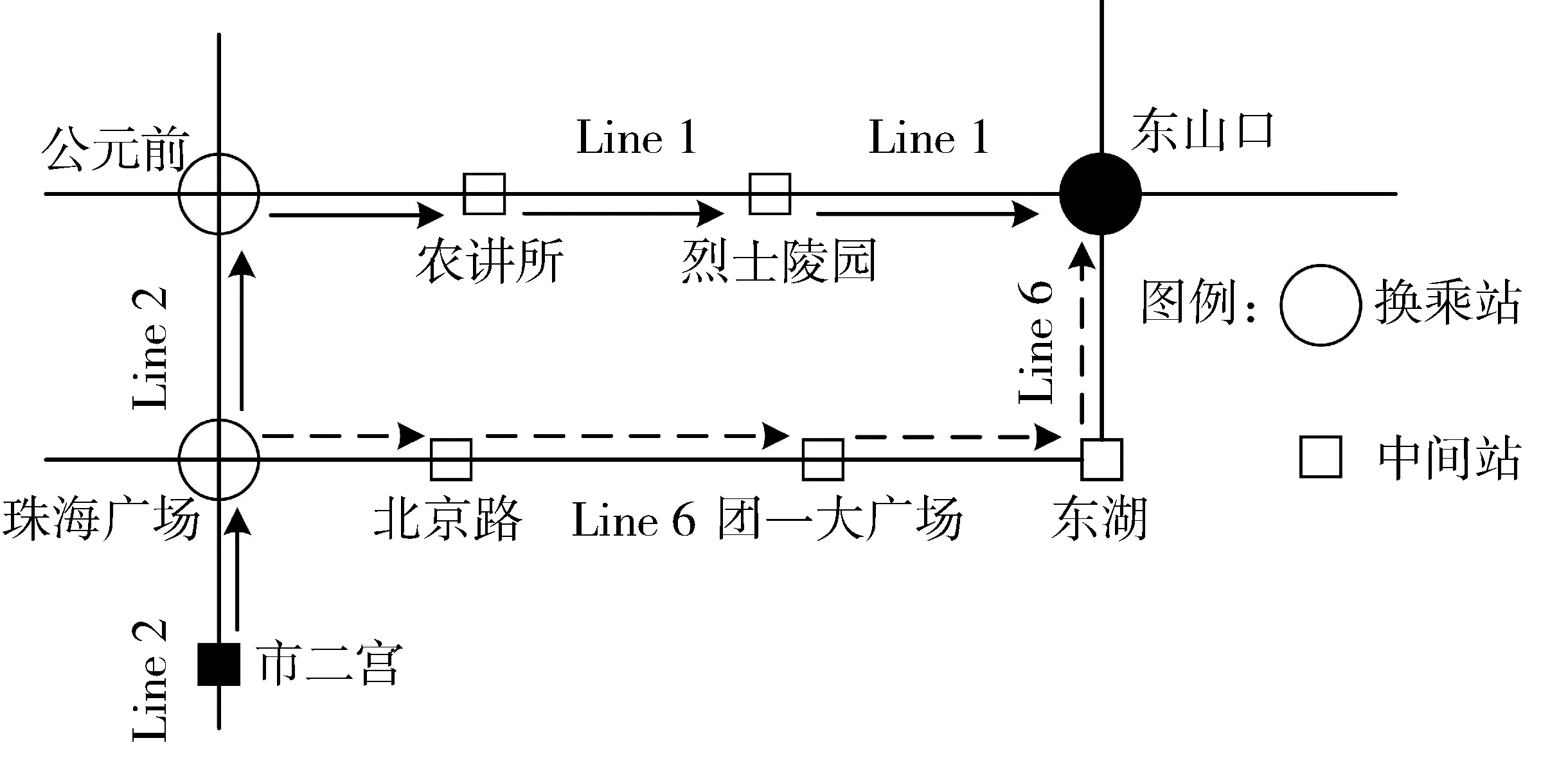
图1 广州地铁线路Fig. 1 Guangzhou subway line map

路径1：市二宫→海珠广场→公元前(2换1)→农讲所→烈士陵园→东山口。

路径2：市二宫→海珠广场(2换6)→北京路→团一大广场→东湖→东山口。

根据文中路网客流分配计算方法，将市二宫至东山口OD间客流分配到两条有效路径方法如下：

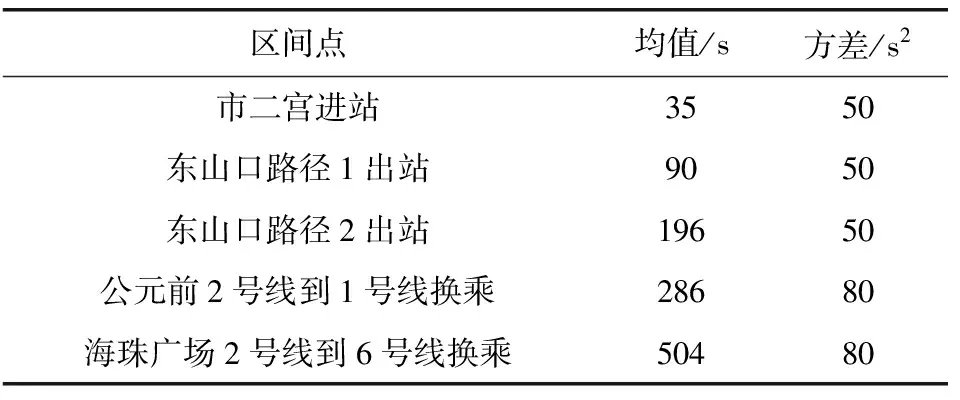
表2 行程时间参数估计Table 2 Parameter estimation of travel time

表3 相关线路的列车发车间隔时间Table 3 Interval schedule of relative lines

笔者采用仿真实验对轨道交通网络客流分配模型进行检验。已知两条有效路径乘车时间分别为：543、554 s。试验条件为：根据以往AFC数据统计，在工作日07：00—09：00时间段内客流，在体育中心站内，随机产生500名乘客，按照不同比例分配到两条路径上，以此理论来进行仿真实验，实验结果如图2。

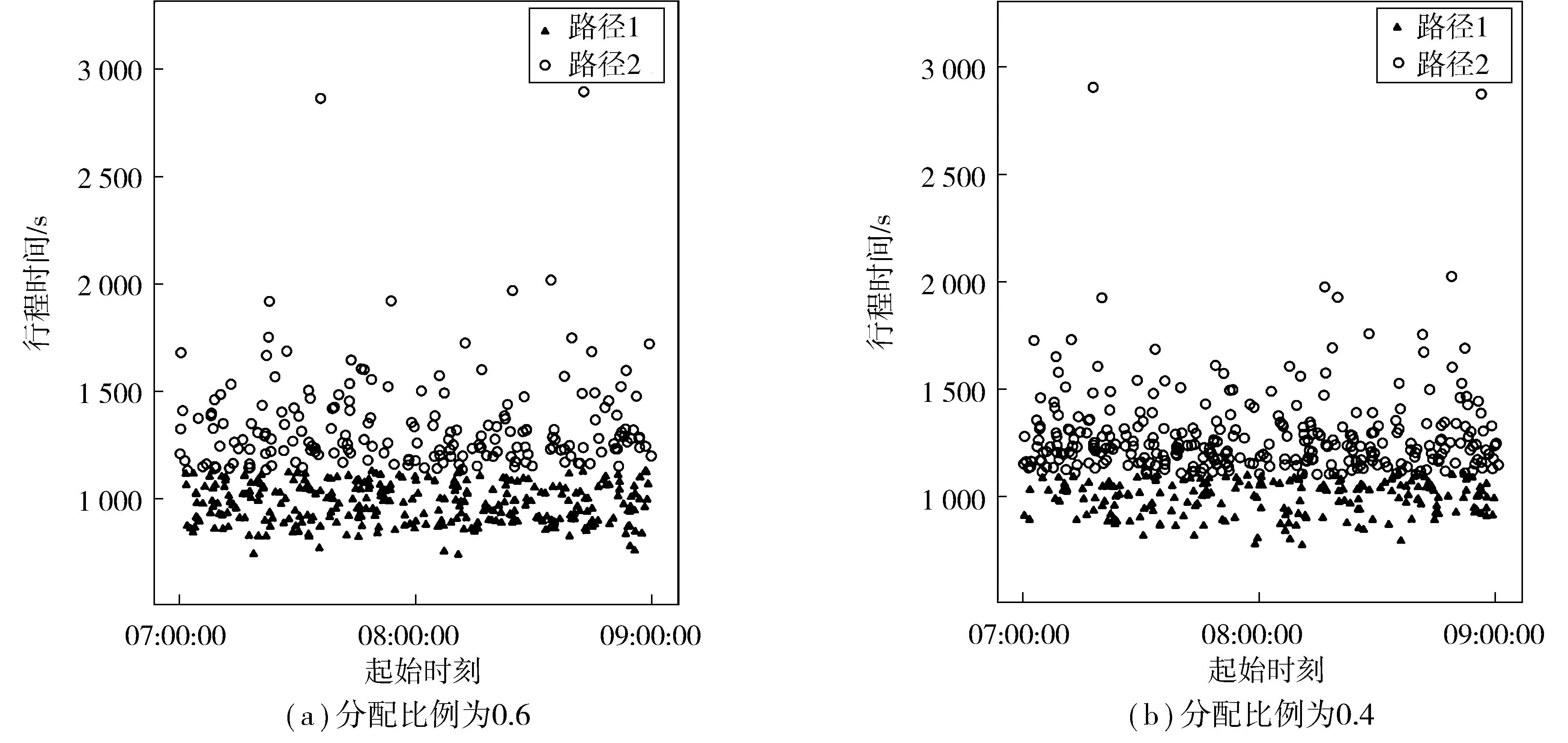
图2 路网OD间客流在两条路径分配结果Fig. 2 Distribution results of OD passengers flow in two paths

经过计算，在不同的分配比例下，两条路径的预测值及误差如表4。根据实验结果可知：对两条路径客流不同的分配比例，笔者的方法均能实现较好预测结果。

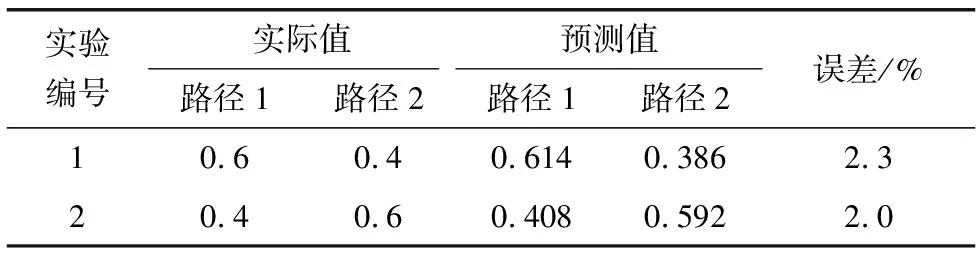
表4 路网客流分配结果Table 4 Result of passenger flow distribution in road network

4 结 语

笔者基于实际乘客AFC数据基础上，得到轨道交通网络每条路径行程时间的均值与方差，然后根据已有行程时间的均值和方差，结合朴素贝叶斯分类器将每名乘客作为一个样本进行概率分类，提出了一种基于朴素贝叶斯的轨道交通网络客流分配模型。

经过相关算例验证及仿真实验结果表明：该方法能很好预测网络客流在每条有效路径上的分配。然而，笔者的研究没有区分高峰和平峰时段，在不同时间段内，客流量会有所不同，行程时间也会有所差异，对最后预测结果影响有待进一步研究。

参考文献(References)：

[1] 徐瑞华，罗钦，高鹏.基于多路径的城市轨道交通网络客流分布模型及算法研究[J].铁道学报，2009，31(2)：110-114.

XU Ruihua，LUO Qin，GAO Peng.Passenger flow distribution model and algorithm for urban rail transit network based on multi-route choice[J].JournaloftheChinaRailwaySociety，2009，31(2)：110-114.

[2] RODRIGUEZ J.A constraint programming model for real-time train scheduling at junctions[J].TransportationResearchPartB：Methodological，2007，41(2)：231-245.

[3] WENDLER E.The scheduled waiting time on railway lines[J].TransportationResearchPartB：Methodological，2007，41(2)：148-158.

[4] 四兵锋，毛保华，刘智丽.无缝换乘条件下城市轨道交通网络客流分配模型及算法[J].铁道学报，2007，29(6)：12-18.

SI Bingfeng，MAO Baohua，LIU Zhili.Passenger flow assignment model and algorithm for urban railway traffic network under the condition of seamless transfer[J].JournaloftheChinaRailwaySociety，2007，29(6)：12-18.

[5] ZHOU Feng，XU Ruihua.Model of passenger flow assignment for urban rail transit based on entry and exit time constraints[J].JournaloftheTransportationResearchRecord，2012，2284(1)：57-61.

[6] SUN Yanshuo，XU Ruihua.Rail transit travel time reliability and estimation of passenger route choice behavior：analysis using automatic fare collection data[J].JournaloftheTransportationResearchRecord，2012，2275(1)：58-67.

[7] SI Bingfeng，ZHONG Ming，LIU Jianfeng，et al.Development of a transfer-cost-based logit assignment model for the Beijing rail transit network using automated fare collection data[J].JournalofAdvancedTransportation，2013，47(3)：297-318.

[8] JOANNE C.RailTransitODMatrixEstimationandJourneyTimeReliabilityMetricsUsingAutomatedFareData[D].Cambridge，MA，USA：Massachusetts Institute of Technology，2007.

[9] KUSAKABE T，ASAKURA Y.Behavioural data mining of transit smart card data：a data fusion approach[J].TransportationResearchPartC：EmergingTechnologies，2014，46：179-191.

[10] KUSAKABE T，IRYO T，ASAKURA Y.Estimation method for railway passengers’ train choice behavior with smart card transaction data[J].Transportation，2010，37(5)：731-749.

[11] MA Xiaolei，WANG Yinhai，CHEN Feng，et al.Transit smart card data mining for passenger origin information extraction[J].JournalofZhejiangUniversityScienceC：Computer&Electronics，2012，13(10)：750-760.

[12] WANG Ya，DU Bowen，RONG Qiannan，et al.Travel patterns analysis of urban residents using automated fare collection system[J].ChineseJournalofElectronics，2016，25(1)：40-47.

[13] 朱顺应，吴俣，王红，等.轨道交通乘客满意度不确定性预测与分析[J].重庆交通大学学报(自然科学版)，2015，34(6)：150-155.

ZHU Shunying，WU Yu，WANG Hong，et al.Uncertainty prediction and analysis on rail passenger satisfaction[J].JournalofChongqingJiaotongUniversity(NaturalScience)，2015，34(6)：150-155.

[14] 石俊刚，周峰，朱炜，等.基于AFC数据的城轨乘客出行路径选择比例估计方法[J].东南大学学报(自然科学版)，2015，45(1)：184-188.

SHI Jungang，ZHOU Feng，ZHU Wei，et al.Estimation method of passenger route choice proportion in urban rail transit based on AFC data[J].JournalofSoutheastUniversity(NaturalScienceEdition)，2015，45(1)：184-188.

[15] 张轮，杨文臣，刘拓，等.基于朴素贝叶斯分类的高速公路交通事件检测[J].同济大学学报(自然科学版)，2014，42(4)：558-563.

ZHANG Lun，YANG Wenchen，LIU Tuo，et al.A naive bayesian classifier-based algorithm for freeway traffic incident detection[J].JournalofTongjiUniversity(NaturalScience)，2014，42(4)：558-563.