Reactivity of Indoles through the Eyes of a Charge-Transfer Partitioning Analysis

OROZCO-VALENCIA Ulises , GÁZQUEZ José L. , VELA Alberto ,*

1 Departamento de Química, Centro de Investigación y de Estudios Avanzados, Av. Instituto Politécnico Nacional 2508, Colonia San Pedro Zacatenco, Ciudad de México, 07360, México.

2 Departamento de Química, Universidad Autónoma Metropolitana-Iztapalapa, Av. San Rafael Atlixco 186, Ciudad de México, 09340,México.

1 Introduction

Chemical reactivity within density functional theory(CRDFT) is a very active field that studies chemical transformations1–8. Aiming to justify the Hard-Soft Acids-Bases principle (HSAB)9, Parr and Pearson developed a simple approach to study chemical reactivity assuming that the energy of a chemical system is a smooth and differentiable function of the number of electrons that can be represented as a quadratic function of this variable, we call this procedure the Parr and Pearson model (PP)10. This model is supported by the Taylor expansion of the energy as a function of the number of electrons keeping constant the external potential, leading to the emblematic PP expression ΔE = μΔ N +η(Δ N )2for the change in the energy as a function of the change in the number of electrons, ΔN, where μ and η are the electronic chemical potential and the global hardness. This simple model has explained many aspects of chemical reactivity that are well documented in the literature. The change in the energy involved in an association reaction such as A + B → AB can be approximated as Δ EAB≅ ΔEA+ΔEB, where the change in the energy of each reactant is evaluated according to the expression mentioned above for the change of the energy in terms of the corresponding change in the number of electrons. Minimizing ΔEABwith respect to the amount of charge transferred and using the constraint that the number of electrons is conserved,one obtains that

Considering that the global hardnesses of both species are positive, the direction of electron flow is determined by the chemical potential difference. Thus, if μA＞ μBthen ΔNA＜ 0,meaning that A is the nucleophile (species donating electrons)and B the electrophile (species accepting electrons)1,10.According to Pearson if the number of electrons transferred in an association reaction is large, it is likely that it may have a low activation barrier, and he used this amount of charge transferred to rationalize the reactivity of several organic and inorganic reactions, founding a good correlation between Eq.(1) with kinetic and equilibrium constants11,12. The applicability of this ansatz stands on the fact that the molecular structure of the transition state is complied by the two fragments having geometries very similar to those of the free reactants or, in other words, that this reaction has an early transition state(ETS), in agreement with Hammond’s postulate13. In fact, this is the scenario where one expects that CRDFT will have better predicting capabilities14,15.

Recently we presented a partitioning scheme for the number of electrons exchanged in an association chemical reaction considering that both species accept and donate charge, aiming to determine the charge-transfer mechanism, electrophilic or nucleophilic, prevailing in the reaction16,17. We showed that the global change in the number of electrons of reactant (fragment)A can be written as

where

is the nucleophilic channel, and

the electrophilic channel. In Eqs. (3) and (4), I and A are the vertical ionization potential and electron affinity, respectively,of the corresponding species, that are determined by the energy differences: I = E(N – 1) − E(N) and A = E(N) − E(N + 1). This partitioning scheme has been successfully used to quantify the amount of charge transferred by σ donation and π-backdonation in transition metal (TM) ligand interactions17. The global charge transfer partitioning just described was complemented with a local version that through the atomic condensed Fukui functions of the reactants allowed us to establish which are the most relevant atoms of each reactant participating in the reaction16. Therefore, in Ref.16 and Ref. 17 it is shown that this global and local partitioning provides scales, through the amount of charge transferred that can serve as alternative reactivity scales.

The aim of the present work is to apply this global and local charge transfer partitioning model to explain the experimental kinetic constants for a set of indoles studied by Mayr18, paying special attention to the conclusions provided by the analysis of the most reactive atoms in these reactions.

2 Local model: a summary

In this section we very briefly describe the procedure that leads to the working equations of the local model including the partitioning that distinguishes charge transfer channels as electrophilic or nucleophilic, for each reactant and leads to determine which are the key atoms involved in the reaction. For mathematical details we refer the reader to Ref. 16. The derivation starts considering the functional Taylor expansion of E[ρ(r)], truncated to second order, and assuming that the changes in the electron density Δρ(r) are only due to electron transfer; then Δρ(r) = f(r)ΔN, where f(r) is the Fukui function(FF)19,20. Introducing an atomic resolution for the FFs we obtain the following expression for the energy change of a reactant

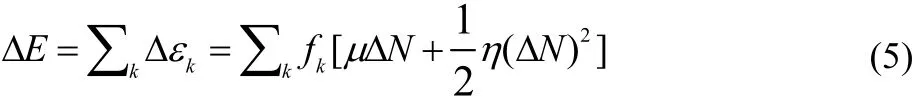
where fkis the Condensed Fukui Function (CFF) of the k-th atom in the corresponding molecule21–24.

A key consideration in our local model is that we will not include all atoms of each reactant in the evaluation of the change in its energy. Instead, we will include a atoms from reactant A and b atoms from reactant B. Therefore, the change in the energy due to the changes on each reactant is given by

where we use the subindex ab in Δε to indicate that this energy change takes into consideration a atoms of reactant A and b from reactant B. It is worth noting that when a and b are equal to the total number of atoms in the reactants, Eq. (6) reduces to the global model, as it should. The selection of atoms follows the criterion that large values of the FF correspond to more reactive sites in a chemical species. Thus, the atoms are ranked depending on their CFF values and the first to be included are those with larger values of their CFFs. Minimizing Eq. (6) with respect to ΔNA, using the constraint that the total number of electrons is conserved leads to the following expression for the amount of charge transferred to reactant A when considering a atoms of A and b atoms of reactant B:

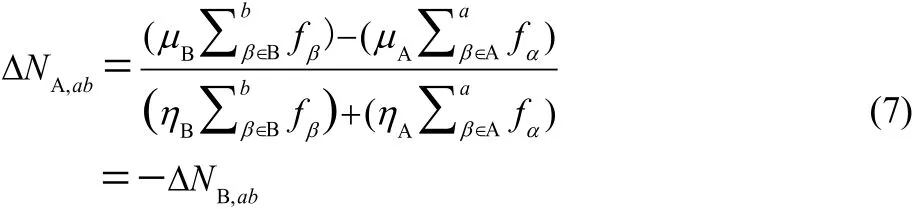
By assuming that the association reactions is such that A is the nucleophile and B the electrophile, one can use the nucleophilic CFF for atom α in A, f−α, and the electrophilic CFF for atom β in B, f+β. Following the same partitioning procedure used in the global model leads one to the following working equations to evaluate the nucleophilic charge transferred when considering a atoms of A and b atoms B:

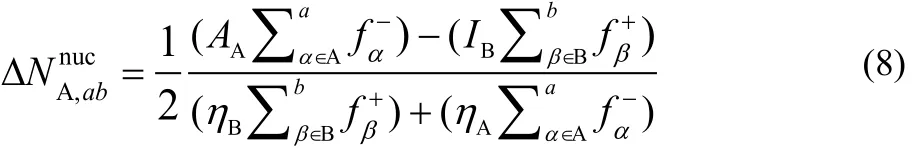
Proceeding analogously one can show that for the electrophilic channel,

Eqs. (8) and (9) are the working expressions that we will use below to illustrate how they can be used to determine which are the most important atomic sites of the reactants participating in the reaction.

3 Computational details

Unless otherwise stated, all calculations reported in this work were made with Gaussian 09 (G09)25using the PBE functional26,27and the 6-311G(d,p) basis set, and in gas phase. A frequency analysis was done on every molecule to confirm that the stationary points located by the optimization procedure were minima in the potential energy surface. The CFFs were determined through the response-of-molecular-fragment approach24, with Yang and Mortier’s scheme21where f+k=qk(N) −qk(N + 1) is the electrophilic CFF and f−k= qk(N − 1) −qk(N) is the nucleophilic CFF, and qkis the charge of the k-atom in the molecule having N, N + 1 and N - 1 electrons. The atomic charges were obtained with Hirshfeld’s Population Analysis (HPA)28. The Fukui functions were evaluated following their the definitions1,19: f−(r) = ρN(r) − ρN−1(r) for the nucleophilic function, and f+(r) = ρN+1(r) − ρN(r) for the electrophilic function, where ρk(r) is the electronic density of molecule having k = N, N + 1 and N - 1 electrons, respectively.For the rendering of the FFs we used VMD, version 1.9.129.

4 Reactions between indoles and 4,6-dinitrobenzofuroxan

In this section we apply the global and local charge transfer partitioning model described above to the reaction between a set of indoles and 4,6-dinitrobenzofuroxan (DNBF). These reactions have been thoroughly analyzed by Mayr and his group18. The set of indoles, considered as reactants A, and DNBF, as reactant B (the common substrate) are shown in Fig.1. To determine which is the prevailing electron transfer channel in the reaction, we analyze first the global charge transfer. In Table 1 we present the global reactivity indexes for the indoles considered here and for DNBF, in addition to the global charge transferred and the electrophilic and nucleophilic partition charges evaluated by Eqs. (1), (3) and (4). Also shown are the experimental kinetic constants taken from the work of Mayr18.

Fig. 1 a) Indoles with ―X (―NH2, ―OH, ―MeO,―Me, ―H, ―Cl, ―CO2H, ―CN) substituents; b) DNBF.

Table 1 Global reactivity indexes, vertical ionization potential (I),electron affinity (A), chemical potential (μ) and hardness (η); total charge transfer (ΔN), electrophilic (ΔN ele) and nucleophilic charge-transfer (ΔN nuc) channels obtained with the PBE exchange-correlation functional and the experimental kinetic constants taken from Ref. 18.

To determine which is the dominant charge transfer channel in the reaction, in Ref. 16 we postulated that the prevailing charge transfer channel is that where the amount of electrons transferred goes parallel with the direction where the reactions proceeds faster. Hence, from the data reported in Table 1 we conclude that the nucleophilic channel is the dominant electron transfer mechanism in the reaction since the trend obtained with iΔN Anuci is in general agreement with that observed in the experimental kinetic constants. Therefore we can conclude that nucleophilicity of indoles toward DNBF is the main electronic process in the initial stages of these reactions. Fig. 2 depicts the good correlation obtained between the nucleophilic charge transfer channel and the experimental kinetic constants. This provides graphical support to the previous conclusion: the charge transfer mechanism prevailing in the reaction between substituted indoles and DNBF is a nucleophilic one on the indoles, i.e., in all cases they are donating charge to DNBF through the nucleophilic channel. We can also suggest that ΔN Anuccan be used or considered as a nucleophilic scale for indoles when reacting with DNBF given that the ordering provided by this global descriptor is in agreement with the scale presented by Mayr and collaborators18. To illustrate the role played by exact exchange in the prediction of the charge transferred by our model, in Table 2 we report the global reactivity indexes obtained using M06-2X30and the 6-311G(d,p)basis set, and in Fig. 3 we depict the correlation between the nucleophilic charge transferred predicted by this functional and the experimental kinetic constants. One can see that the trends are the same, independently of the exchangecorrelation functional, but the inclusion of exact exchange does improve the correlations. With GGA (PBE) we obtain a value of R2= 0.978 and with a global hybrid (M06-2X), R2= 0.982.The reason for the improvement comes from the fact that the vertical ionization potentials and electron affinities are better predicted with global hybrids.

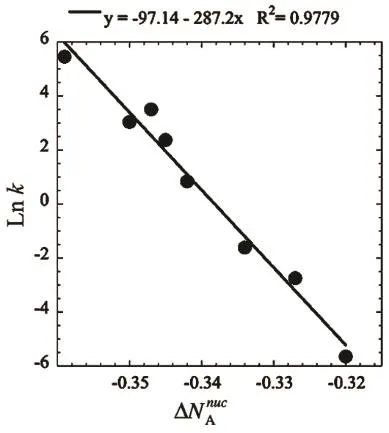
Fig. 2 Correlation between the PBE nucleophilic channel and the experimental kinetic constants.

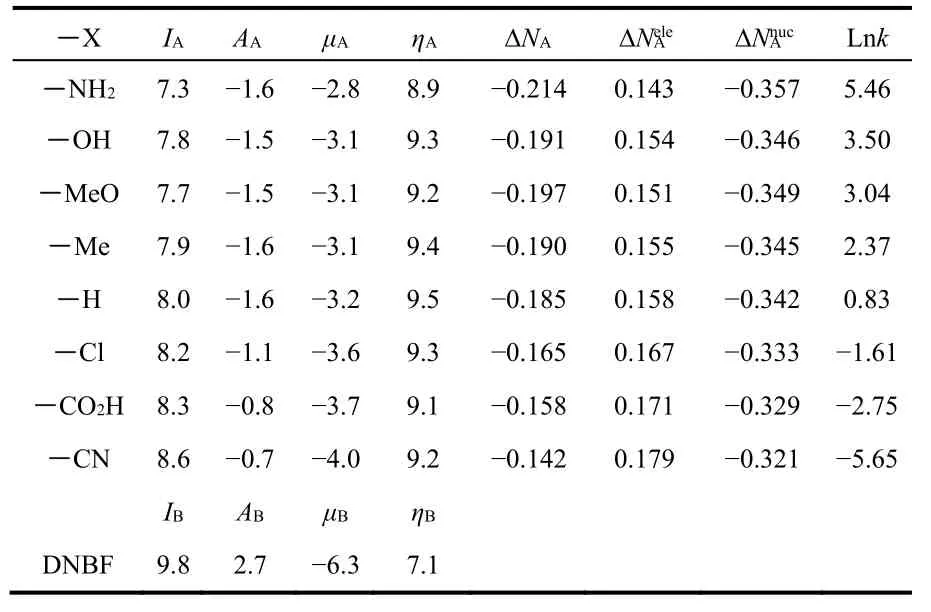
Table 2 Global reactivity indexes, vertical ionization potential (I),electron affinity (A), chemical potential (μ) and hardness (η);total charge transfer (ΔN), electrophilic (ΔN ele) and nucleophilic charge-transfer (ΔN nuc) channels obtained with the M06-2X exchange-correlation functional and the experimental kinetic constants taken from Ref. 18.

We now use the local model to illustrate its utility to identify the most reactive atoms on each reactant. In Table 3 we show the nucleophilic CFFs for the indoles considered in this work and the electrophilic CFFs of DNBF. The atoms of both reactants are labeled as shown in Fig. 1. For reasons that are clarified below, we decided to select the seven larger values of each reactant.

With the values of the CFFs shown in Table 3 and the ionization potentials and electron affinities reported in Table 1,the local nucleophilic channel for each indole was evaluated according to Eq. (8) taking different combinations of reactive atoms between indoles (a-atoms, first subindex) and DNBF(b-atoms, second subindex). For each a and b combination of atoms in the indoles and DNBF, respectively, we evaluated the corresponding correlation coefficient (R2) between Δand the experimental kinetic constants. These correlations coefficients are reported in Table 4.

Fig. 3 Correlation between the M 06-2X nucleophilic channel and the experimental kinetic constants.

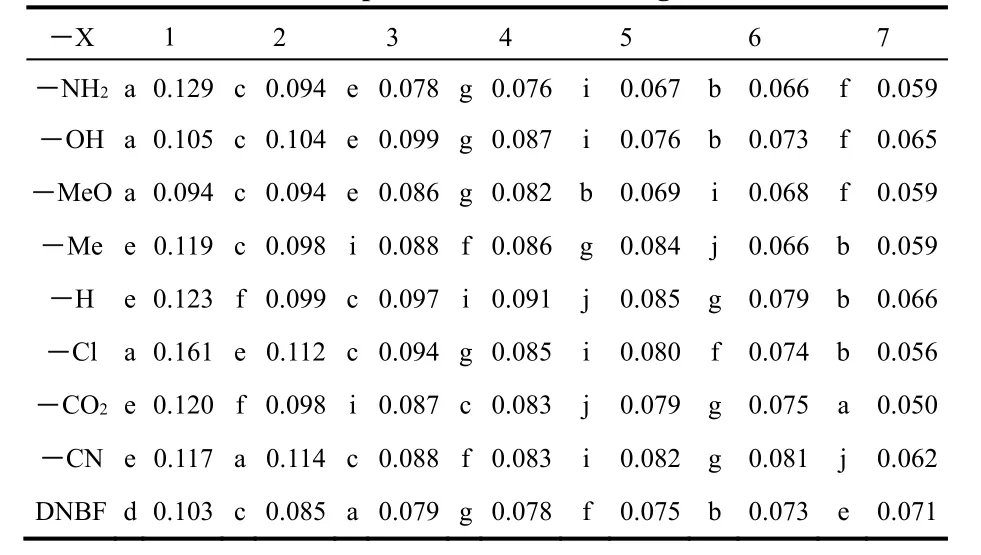
Table 3 The CFFs values for the indoles and DNBF according to the atomic positions defined in Fig. 1.

Table 4 shows two clear tendencies. First, when increasing the number of reactive atoms in the indoles (index a),independently of the number of reactive atoms considered in DNBF, the correlation coefficients increase monotonically, i.e.,they have better correlations. Secondly, and in contrast with the previous observation, the situation is completely opposite with respect to DNBF where, in all cases, the correlations decrease monotonically as more reactive atoms in DNBF are considered.The global picture indicates that for these reactions the best correlation would correspond to that obtained with the global partitioning or, in other words, to include all atoms in the evaluation of the Δ. In our previous applications of the model we found that there was an optimum number of atoms on each reactant providing the maximum correlation and,consequently, going beyond this number of atoms worsened the correlations. Thus, in the present case, considering that the global correlation is very good and that the main intention with the local partitioning is to identify the most reactive atoms in the reactants, we decided to limit the number of atoms in the indoles to seven. In fact, to provide a more concrete selection of reactive sites one could limit the number of relevant atom to 4 considering that Table 4 shows that the improvement in the correlations is marginal when the number of atoms in the indoles goes beyond a = 3. Then, using the combination ab =32, i.e., taking the first three atoms in the indoles and the 2 atoms in DNBF that have the larger values of the CFFs, and from the data reported in Table 3, we find that the atoms playing the most important roles in the reaction are: in the indoles atoms a, c, e, f, and i; in DNBF, atoms c and d.Considering the most frequent appearance of the atoms in the eight indoles we can say that atoms c and e are the most likely atoms to participate in the reaction. It should be noted that for indoles with electron donating substituents the atom different from carbon in the group is, according to their CFFs values, the most likely atom to suffer the attack.

We now use the information obtained above regarding the most reactive atoms together with spatial distribution of the FFs to propose a plausible starting geometry orientation betweenindoles and DNBF that could drive the system to the transition state. In Fig. 4 we present isosurface plots of the electrophilic and nucleophilic FFs of one indole (X = ―H) and DNBF.According to Fig. 4a the initial intermolecular binding between indoles and DNBF happens on the molecular plane since this orientation seems to maximize the overlap between the FFs;note that the nucleophilic FF of the indole covers the zone of C(e) atom and, moreover, the electrophilic FF of DNBF also covers the C(c) and C(d) atoms. Second, in Fig. 4b we show the isovalue plots of the electrophilic FF of the indole and the nucleophilic one of DNBF. These plots can provide further support to propose a molecular orientation in the binding between the indole and DNBF. In this case, the isosurface plots suggest that the overlap between the oxygen atom (position d)in DNBF and the carbon atom of the indole in position f are the most likely interacting sites. It is important to comment that this oxygen atom in DNBF has also a large negative charge in addition to a large nucleophilic CFF value, and that the carbon atom of indole in position f also has a low negative charge and a large electrophilic CFF value. This interaction by alienation of nucleophilic/electrophilic zones of DNBF and indole is feasible due to the proximity between C(e) and C(f) atoms in the indole. Moreover, note that the intermolecular binding suggested by our analysis and the alienation of nucleophilic/electrophilic zones between indole and DNBF produces a six-member ring that can stabilize this structure and makes it a good candidate to start searching for the TS of the reaction.Therefore, these isosurface plots of the FFs of indole and DNBF together with the knowledge about the most reactive atoms we can propose that the attack of the indole on DNBF may occur as shown in Fig. 5. Similar findings were obtained for the other indoles.

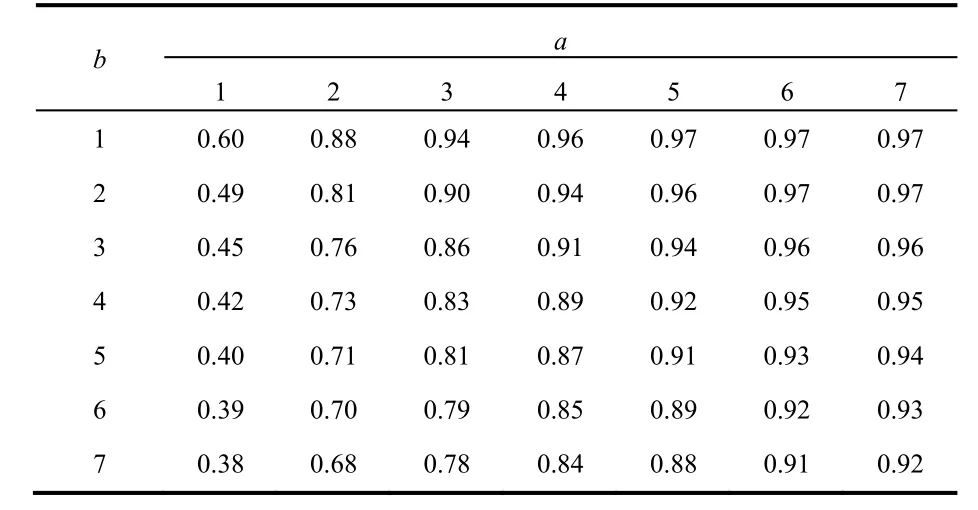
Table 4 Correlations coefficients (R2) between the local nucleophilic channel of indoles and the experimental kinetic constants, for different combinations of reactive atoms in the indole (a) and in DNBF (b).

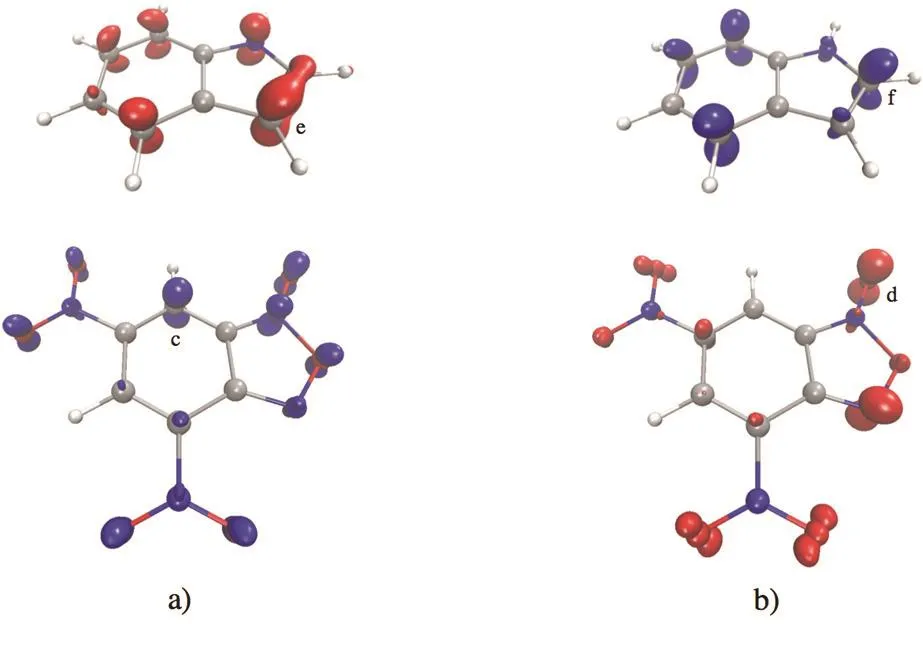
Fig. 4 Isosurface plots of the Fukui Function (nucleophilic in red and electrophilic in blue), using an isovalue of 0.007, for the indole with X = ―H and DNBF.

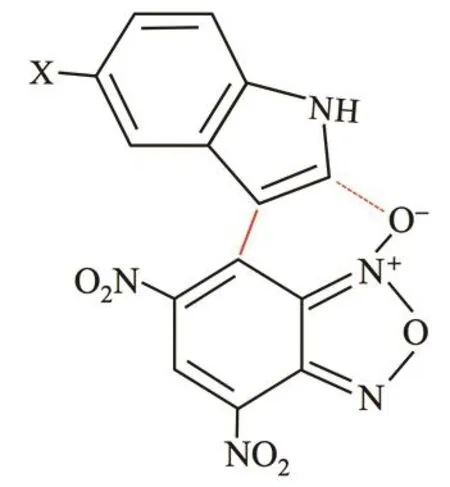
Fig. 5 Schematic representation of the interaction between indoles and DNBF.

It is important to note that this analysis about the initial stages of the reaction mechanism between indoles and DNBF is in agreement with the experimental evidence about the intermolecular binding site between reactants31. Moreover, our conclusion that the nucleophilicity of indoles controls its reactivity towards DNBF is also in agreement with the experimental results of Mayr and other theoretical works using CRDFT18,32.

5 Summary and conclusions

In this work we applied a global and local partitioning model of charge transfer to the nucleophilicity of indoles reacting with 4,6-dinitrobenzofuroxan. The global model leads us to conclude that the reaction is controlled by a nucleophilic attack on the indoles, in agreement with the experimental conclusion.The nucleophilic charge transferred is in excellent agreement with the nucleophilic ordering proposed by Mayr and collaborators suggesting that this global reactivity index can be used as nucleophilic scale for the reactivity of indoles. The local analysis of the nucleophilic channel indicates that the atoms playing the most relevant roles in the reactions are C(c)and C(e) of indoles and the C(c) of 4,6-dinitrobenzofuroxan.Using the information provided by the local analysis and the spatial distribution of the electrophilic and nucleophilic Fukui functions of the indoles and 4,6-dinitrobenzofuroxan, we show that one can suggest molecular structures that can describe the first stages of the interactions between these reactants that can be used as starting geometries for the transition state search of these reactions. The analysis suggests the existence of an alienation of nucleophilic/electrophilic zones between indole and DNBF that produces a six-member ring.

Acknowledgment:We thank the Laboratorio Nacional de Cómputo de Alto Desempeño (LANCAD) for the use of their facilities.

(1) Parr, R. G.; Yang, W. Density-Functional Theory of Atoms and Molecules, Revised ed.; Oxford University Press: New York, NY,USA, 1994.

(2) Chermette, H. J. Comput. Chem. 1999, 20, 129.doi: 10.1002/(Sici)1096-987x(19990115)20:1＜129::Aid-Jcc13＞3.0.Co;2-A

(3) Geerlings, P.; De Proft, F.; Langenaeker, W. Chem. Rev. 2003, 103,1793. doi: 10.1021/cr990029p

(4) Gázquez, J. L. J. Mex. Chem. Soc. 2008, 52, 3.

(5) Liu, S. B. Acta Phys. -Chim. Sin. 2009, 25, 590.doi: 10.3866/Pku.Whxb20090332

(6) Chattaraj, P. K.; Sarkar, U.; Roy, D. R. Chem. Rev. 2006, 106, 2065.doi: 10.1021/cr040109f

(7) Chattaraj, P. K.; Roy, D. R. Chem. Rev. 2007, 107, PR46.doi: 10.1021/cr078014b

(8) Chattaraj, P. K.; Giri, S.; Duley, S. Chem. Rev. 2011, 111, PR43.doi: 10.1021/cr100149p

(9) Pearson, R. G. Coord. Chem. Rev. 1990, 100, 403.doi: 10.1016/0010-8545(90)85016-l

(10) Parr, R. G.; Pearson, R. G. J. Am. Chem. Soc. 1983, 105, 7512.doi: 10.1021/Ja00364a005

(11) Pearson, R. G. Inorg. Chem. 1988, 27, 734.doi: 10.1021/ic00277a030

(12) Pearson, R. G. J. Org. Chem. 1989, 54, 1423.doi: 10.1021/jo00267a034

(13) Anslyn, E. V.; Dougherty, D. A. Modern Physical Organic Chemistry; University Science Books: Sausalito, CA, USA, 2005.

(14) Ayers, P. W.; Anderson, J. S. M.; Bartolotti, L. J. Int. J. Quantum Chem. 2005, 101, 520. doi: 10.1002/qua.20307

(15) Roos, G.; Geerlings, P.; Messens, J. J. Phys. Chem. B 2009, 113,13465. doi: 10.1021/jp9034584

(16) Orozco-Valencia, A. U.; Gazquez, J. L.; Vela, A. J. Phys. Chem. A 2017, 121, 4019. doi: 10.1021/acs.jpca.7b01765

(17) Orozco-Valencia, U.; Gazquez, J. L.; Vela, A. J. Mol. Model. 2017,23, 207. doi: 10.1007/s00894-017-3368-y

(18) Lakhdar, S.; Westermaier, M.; Terrier, F.; Goumont, R.; Boubaker,T.; Ofial, A. R.; Mayr, H. J. Org. Chem. 2006, 71, 9088.doi: 10.1021/jo0614339

(19) Parr, R. G.; Yang, W. T. J. Am. Chem. Soc. 1984, 106, 4049.doi: 10.1021/ja00326a036

(20) Berkowitz, M. J. Am. Chem. Soc. 1987, 109, 4823.doi: 10.1021/ja00250a012

(21) Yang, W.; Mortier, W. J. J. Am. Chem. Soc. 1986, 108, 5708.doi: 10.1021/ja00279a008

(22) Fuentealba, P.; Perez, P.; Contreras, R. J. Chem. Phys. 2000, 113,2544. doi: 10.1063/1.1305879

(23) Ayers, P. W.; Morrison, R. C.; Roy, R. K. J. Chem. Phys. 2002, 116,8731. doi: 10.1063/1.1467338

(24) Bultinck, P.; Fias, S.; Van Alsenoy, C.; Ayers, P. W.; Carbo-Dorca,R. J. Chem. Phys. 2007, 127, 034102. doi: 10.1063/1.2749518

(25) Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb,M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, Revision D.01; Gaussian Inc.:Wallingford, CT, USA, 2009.

(26) Perdew, J. P.; Burke, K.; Ernzerhof, M. Phys. Rev. Lett. 1996, 77,3865. doi: 10.1103/PhysRevLett.77.3865

(27) Perdew, J. P.; Burke, K.; Ernzerhof, M. Phys. Rev. Lett. 1997, 78,1396. doi: 10.1103/PhysRevLett.78.1396

(28) Hirshfeld, F. L. Theor. Chim. Acta 1977, 44, 129.doi: 10.1007/bf00549096

(29) Humphrey, W.; Dalke, A.; Schulten, K. J. Mol. Graphics Modell.1996, 14, 33. doi: 10.1016/0263-7855(96)00018-5

(30) Zhao, Y.; Truhlar, D. G. Theor. Chem. Acc. 2008, 120, 215.doi: 10.1007/s00214-007-0310-x

(31) Terrier, F.; Pouet, M. J.; Halle, J. C.; Hunt, S.; Jones, J. R.; Buncel,E. J. Chem. Soc., Perkin Trans. 2 1993, 1665.doi: 10.1039/p29930001665

(32) Domingo, L. R.; Perez, P. Org. Biomol. Chem. 2011, 9, 7168.doi: 10.1039/c1ob05856h