Multiply Charged Anions, Maximum Charge Acceptance, and Higher Electron Affinities of Molecules, Superatoms, and Clusters

VON SZENTPÁLY László

Institut für Theoretische Chemie, Universität Stuttgart, Pfaffenwaldring 55, 70569 Stuttgart, Germany.

1 Introduction

How many excess electrons can be bound by an arbitrary chemical system? In the gas-phase, the capacity of storing negative charge is severely limited, and even the singly charged anions of many common organic molecules are unstable1,2.The instability arises primarily from confining the excess negative charge to a small microscopic volume. Therefore,attaching several electrons to form gas-phase multiply charged anions, MCA’s, is a very challenging task, and requires sophisticated experiments3–5. On the other hand, stabilized MCA’s are ubiquitous in condensed phases, and important for the solid-state- and nano-sciences3–6,.plasma physics7, solution chemistry3,8, organic synthesis9, acid-base and redox reactions1.Dianions are essential even for the bio-regulation of many metabolic and cellular processes in vivo, e.g., sulfate, SO42‒10,11.MCA’s also play a role in atmospheric chemistry12. Therefore the existence and properties of MCA’s have received massively growing attention in the last two decades. This is documented in reviews and research articles addressing fundamental questions about their intrinsic properties3–17. Theoretical calculations of gas-phase MCA properties are extremely demanding, thus the limits of computational feasibility have been frequently reached15. There has been no general method determining the maximum number of bound electrons in MCAs and expressing their electronic stability by calculating,rationalizing and predicting the Q th electron affinity, AQ, for arbitrary systems. By definition, the MCA, XQ−, carrying Q excess electrons is electronically stable, if AQis positive

AQ(X) = E(X(Q−1)−) − E(XQ−) ＞ 0 (1)

Note that the electronic stability of XQ−does not exclude its thermodynamic instability, because the MCA may decompose into smaller ionic fragments carrying the same total charge.

We here consider neutral gas-phase systems, X, of arbitrary size and electron number, N0, and address two central questions:

(i) What is the “maximum charge acceptance”, i.e., the maximum number of excess electrons, Qmax= Nmax− N0, that can be bound by the gas-phase species?

(ii) Is there a simple method to calculate the higher electron affinities, AQ(X), with integer Q ＞ 1, from properties of the“ancestor” system?

In density-functional theory (DFT)18–21and concepts derived from electronegativity21–28the total energy, E(N, v ex), is a continuous function of the average electron number N, and the“external” potential, vex, of the nuclei. Take a chemical species of electron number N0with vertical first ionization energy, Iv=E(N0− 1) − E(N0), and vertical first electron affinity, A1,v=E(N0) − E(N0 + 1). The DFT energy, E DFT(N), consists of straight line segments connecting E(N0− 1), E(N0) and E(N0+1) with slope discontinuities at integer values of N18–29. For N0−1 ＜ N ＜ N0 the negative slope of the segment defines the DFT electronegativity as χDFT= Iv= −∂EDFT/∂N. For N ＞ N0the value of χDFTchanges to A1,vand remains constant up to N0+1 = Nanion17–21,24,29. A direct method to calculate the energy of a dianion would be a straight line extrapolation of the total energy up to N0 + 2 = N dianion. However, the slope discontinuity at Nanionis unknown, unless A2itself is known beforehand. It remains a dilemma of the state-of-the-art DFT that the value of A2 is required as input for finding the continuation of E DFT(N)beyond the anion. Embarrassingly, most DFT exchangecorrelation functionals describe anions as having barely a fraction of the excess electron bound, with the remaining fraction auto-detaching, when the basis sets are increased30.Further limitations of DFT concerning anions have been discussed in17,24,30,31.

At this state of the art, empirical concepts and approximations estimating MCA properties are helpful. Large A1values3,14–17or A1/I ratios21provide guidelines in seeking electronically stable MCA’s. The Wade-Mingos rule32,33on the significance of the number of skeletal bonding electron-pairs in cluster compounds is also useful34. Most current models, such as the homogeneous charged-sphere13,14,35, the liquid-drop36and stabilized-jellium models36,37assume that the difference between AQ−1and AQis determined by the repulsion energy between the two “outermost” electrons3–5,13–16,35–38.Unfortunately, they are not applicable to atoms and small molecules, but limited to large and preferably spherical clusters3–5,35–37. In addition to their AQ−1input data, these models introduce further species-specific parameters, viz.,adjustable diameters, Ø, with electron spill-out corrections, δ,and dielectric constants, ε.

Recently, the electronic stability of dianions, X2−, has been very successfully described by a universal method to calculate the second electron affinity, A2(X)17. Given the I and A1values of the neutral “grandparent” system, the 2nd electron affinity is modelled as A2,calc = A1 − (7/12)(I − A1)17. The equation seems valid for arbitrary gas-phase systems. The comparison with 37 literature reference data of atoms, molecules, and clusters yields A2,ref= 1.004A2,calc− 0.023 eV, the mean unsigned deviation, MUD = 0.095 eV, and the correlation coefficient of R = 0.9987. The aim here is to (i) update and extend the evidence for the simple method and (ii) test it also on very recently documented trianions34, X3‒, and the appearance sizes of triply charged nano-clusters and superatoms. Starting from the Parr-Szentpály-Liu (PSzL) electrophilicity concept21,24, we develop a general method to determine the electronic stability of gas-phase MCA’s of arbitrary size without explicit computation or measurement. The excess negative charge is Q =N − N0.

2 Estimating the maximum charge acceptance by charge dependent electronegativity

To overcome the DFT dilemma of slope discontinuities,second order polynomials, E(Q), together with charge dependent electronegativities, χ(Q), are needed to model the energy in systems, where electrons are transferred or exchanged17–26,28.We consider two types of second order polynomials in extending E(Q) to dianions in: the “valence-state-parabola”, VSP17,22–24,and the “ground-state-parabola”, GSP18–27. The VSP energy polynomial reads (Fig. 1)

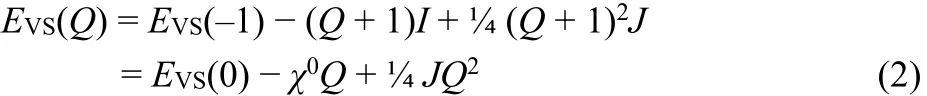
here J = I − A1is a measure of the electron-pair repulsion energy and χ0= ½(I + A1) the Mulliken electronegativity.

The GSP model is used by conceptual DFT18,20,21,24,26. The GSP energy polynomial is (Fig. 1)

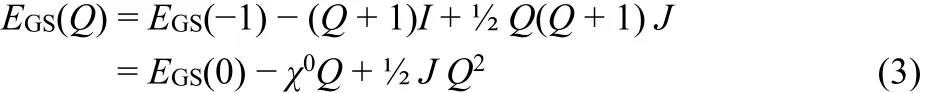
Fig. 1 Normalized energies E(Q)/A1 for the case A1/I = 1/3.

In Fig. 1 we compare normalized VSP, GSP and DFT energies (each divided by A1) in the range −1 ＜ Q ＜ 1, equivalent to N cation ＜ N ＜ N anion17,23‒26. We plot E(Q)/A1 for species with A1/I = 1/3, the ratio observed for borderline cases of gas-phase dianion stability e.g., for the fullerene C70, or the cluster Ag223,17,35. All three curves coincide at Q = −1 and Q = 1. In agreement with the variation principle, EVS(Q) is larger than EDFT(Q) in the present definition range, as EVS(Q) = EDFT(Q) + ¼J(1 − |Q|)2＞ EDFT(Q) is valid for |Q| ＜ 1. The VSP starts at Ecation= E(−1), where its gradient, ∂E VS/∂Q = −I, is in line with DFT theorems 18–21, 29. At N anion it reaches E anion = E(1) with the slope −A1. The VSP model thus satisfies the DFT constraints on∂E/∂Q at both boundaries, Ncationand Nanion(Fig. 1).

In Fig. 2, the valence-pair affinity27or charge dependent valence-state electronegativity, χVS(Q) = −∂EVS/∂Q, connects the exact DFT values χDFT(–1) = I and χDFT(1) = A1 by a straight line, and reproduces Mulliken’s value χ0= ½ (I +A1) at Q = 0

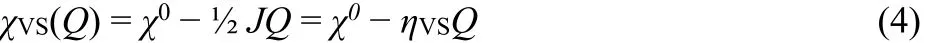
where ηVS= ∂2EVS/∂Q2= ½(I − A1) is the valence-state hardness of the “ancestor” species17,21,23,24.

Fig. 2 illustrates the PSzL argument by plotting different electronegativity functions, χ(Q), for species’ having A1/I = 1/3.According to the PSzL electrophilicity concept, a species, X,may be saturated with excess negative charge to the point Qmax,where the electronegativity χ(Qmax) becomes zero17,21,24. In Fig.2, the realistic molecular case A1/I = 1/3 gives a borderline dianion with Qmax,VS= 2 according to the VSP model, whereas the GSP model predicts Q max,GS = 1 only. For given input data, I and A1 the slope of χGS(Q) is twice that of χVS(Q), with the result

Considering the GSP model we notice the emergence of unphysical solutions, EGS(Q) ＜ EDFT(Q), where the parabola undercuts the line segments representing the exact EDFT(Fig. 1).The gradients ∂E GS/∂Q do not satisfy the DFT conditions at the boundaries N cation and N anion (Fig. 2). This is essentially due to an unphysical electron-electron attraction energy (“self-interaction error”) in Eq. (4) caused by the negative sign of ½ Q(Q + 1) J ＜ 0 in the range −1 ＜ Q ＜ 0.23,24,27Similarly in the range 0 ＜ Q ＜ 1 the electron repulsion energy falls short of that required by exact DFT17,23,24,27. By differentiation of Eq. (3) Parr’s “absolute electronegativity” is obtained as a function of the excess negative charge18,21,24

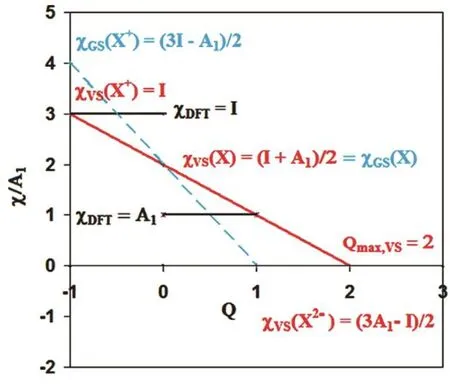
Fig. 2 Electronegativity functions normalized to χ/A1 versus excess negative charge Q, for the case A1/I = .

For the reasons just discussed, the electronegativity χGS(Q)reaches zero at far too small Qmaxvalues. According to the GSP model and conceptual DFT the necessary condition for an electronically stable monoanion is A1(X) ＞ 1/3 I(X) (Fig. 2). This requirement stands in striking contrast to the correct definition of stability that clearly requires A1(X) ＞ 0 only. Unfortunately,conceptual DFT in combination with the PSzL concept generally leads to exaggerated and even unphysical restrictions on the stability of both mono-anions and MCA’s17,21,24. This failure of conceptual DFT has its equivalent in computational DFT, when electronically stable anions are calculated as partially auto-ionized30,31.

The VSP model correctly describes the anion X−as electronically stable with a positive χVS(X−), if A1(X) ＞ 0,because χVS(X−) = A1(X) (Fig. 2). This fact is important to justify extrapolations of χVS(Q) beyond monoanions. For A1/I = 1/3 the valence-state electronegativity χVS reaches zero at Q max,VS = 2(Fig. 2). Generally an MCA can be expected to become electronically stable with

Thus the VSP model provides an MCA-stability criterion along with the maximum uptake of electrons17,21,24. For electronically stable MCA’s Q max,VS ＞ Q is required,

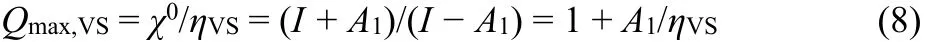
where is calculated from properties of the “ancestor” species. Eq(8) has been already used to estimate the maximum charge acceptance for atoms and molecules back in 199921,24, but then the list did not contain any stable gas-phase MCA, because unambiguous experimental data seemed lacking. Recent publications contain more data of anions with large A1, and both stable and unstable MCA’s3–6,8,17,34–79which may be compared to the predictions of Eq. (8).

As shown in Fig. 2 and Eq. (5) the GSP model of conceptual DFT yields17,21only half the value of Qmax,VS

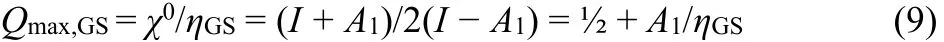
3 Results and discussion

Comparisons with available reference data, A2,lit, indicate that Qmax,VS＞ 2 is a necessary criterion for dianion stability. In fact,molecules with Qmax,VS＞ 2.17 are generally found to have electronically stable gas-phase dianions17. Eq. (8) also supplies a qualitative dianion-stability criterion A1 ＞ η, that is ½(3A1 −I) ＞ 0, and expresses

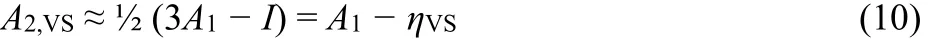
To account for the different and sometimes complex influences, we calibrate the model to molecules having the value A2≈ 017. Several molecules, such as C70, Au11, Ag24, or Cu24,could serve as “anchors”. The fine-tuning to the experimental reference value A2(C70) = 0.02(3) yields17.

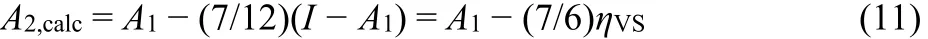
This is a highly efficient universal equation quantifying the electronic stability of dianions of arbitrary size17. Note that other anchor molecules also lead to the same equation. This anchoring further provides the improved maximum charge acceptance as

Table 1 collates the significantly extended and updated Qmaxand A2,calcresults for large varieties of transition-metalcomplexes, ALn, fullerenes, clusters, super-halogens (with electron affinities larger than that of the chlorine atom),super-alkalies (with ionization energies smaller than that of the alkali atoms), and organic molecules. The sample significantly differs from those discussed in Refs. 17 and 21. Fig. 3 shows the correlation

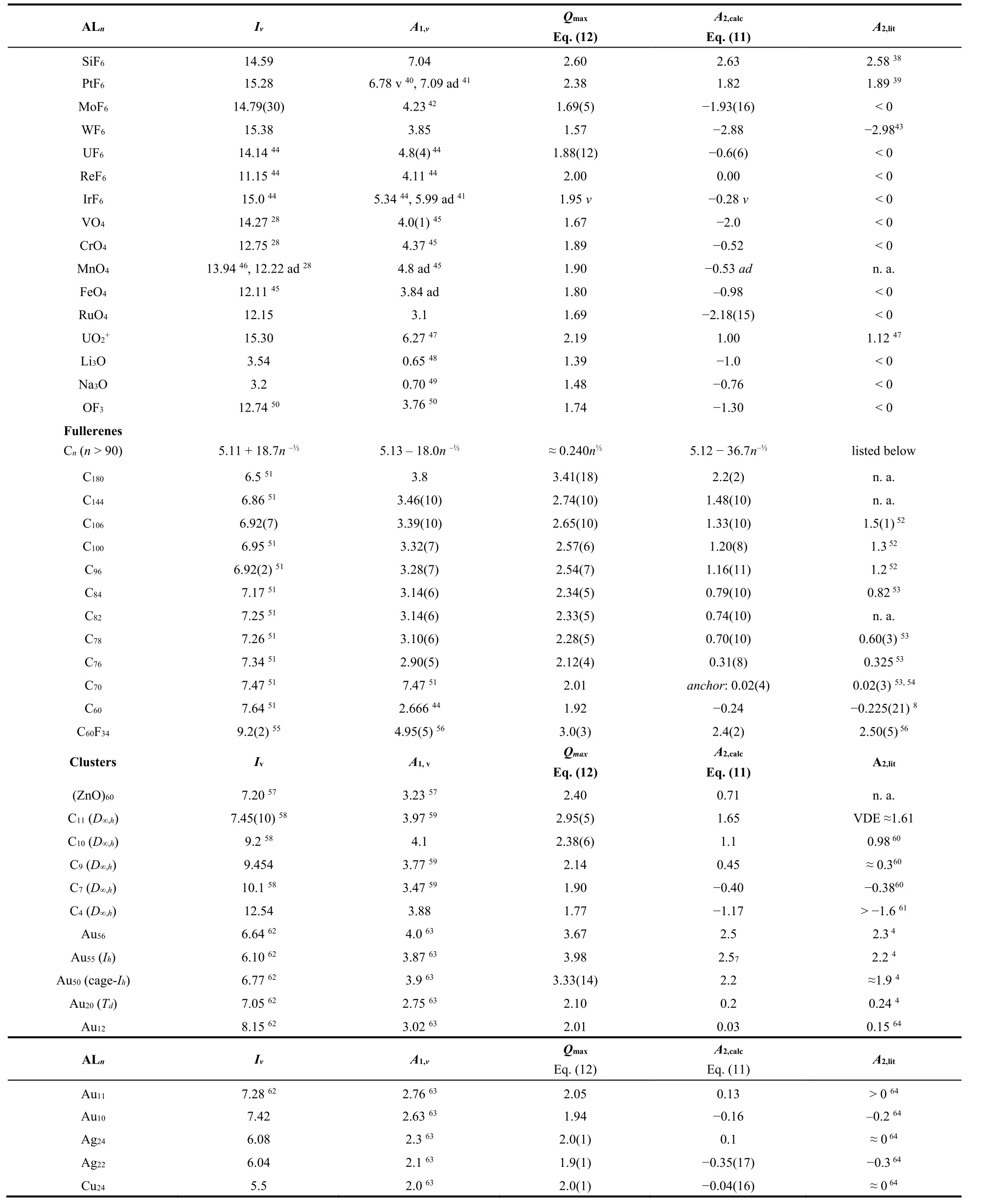
Table 1 Maximum charge acceptance, Q max = 1 + (6/7)A1/ηVS, calculated second electron affinity, A2,calc = A1 − (7/6)ηVS, and literature reference values, A2,lit. Vertical first ionization energies, Iv, and electron affinities, A1,v, from 17,77–79,unless indicated.

continued Table 1

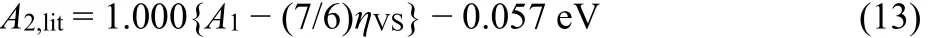
with the correlation coefficient R = 0.998. The mean signed deviation in Eq. (13) is MSD = 0.062 − 0.057 = 0.005 eV, which is below the uncertainty of most of the literature reference data themselves.

Table 2 lists some most recently highlighted super-pnictogens34of the type ABmLn, closo-boranes, B12X12, and other candidates for stable gas phase trianions.

We now discuss selected MCA’s in Tables 1 and 2. The energy unit is eV. Silicon hexafluoride SiF6 is documented having large positive vertical A2,v= 2.3 and adiabatic A2,ad= 2.58 second electron affinities, and the vertical detachment energy,VDE(SiF62−) = 2.7938. With A1,v= 6.8138, A1,ad= 7.0438and Iv=14.5917, Eq. (11) reproduces both the vertical and the adiabatic second electron affinities, A2,v,calc= 2.27 and A2,ad,calc= 2.63. The ionic UO2+indicates that the model may be applied to calculate the 2nd electron affinity of cations. Inserting the computed I(UO2+) = 15.30 and A1(UO2+) = I(UO2) = 6.2747into Eq. (11)yields A2,calc(UO2+) = 1.00 in agreement with the equivalent A1,ref(UO2) = 1.1247. MnO4might be a borderline case, as the dianion is calculated unstable, or stable depending on the reported ionization energies.

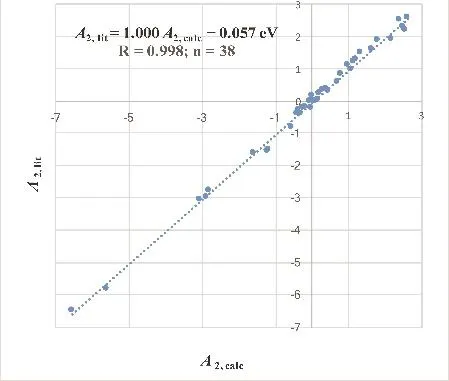
Fig. 3 Linear relationship between 38 calculated second electron affinities, A2,calc, and literature reference values, A2,lit, in eV units.

Fullerenes, Cn, and heterofullerenes, CnXm, are frequently characterized as superatoms, for exhibiting properties of free atoms53‒56. However, in contrast to atoms, superatoms may form stable dianions. We include ten fullerenes and C60F3455. Table 1 shows the very satisfactory agreement. The nanocluster (ZnO)60is shapewise fullerene like57. It is here predicted to accept an additional second electron. Recent computations on the diatomic dianion Cl22−give= −5.82 and agree very well with the prediction A2,calc = −5.61 by Eq. (11), where the appropriate valence-state ionization energy I VS,v(Cl2) = 16.08 is taken71.

Table 2 includes the exciting new class of super-pnictogens,for which stable trianions have been theoretically predicted very recently34. The gas phase stabilities of BeB11(X)132−(X = CN,BO) have been reported as exceptionally high, and the third electron affinities computed, e.g., A3,ad(BeB11(CN)12) = 2.65.The results are here compared with our general model, by taking the monoanion as the ancestor system, since the ionization energy of the neutral system is not known.

For ZrF6, the criterion Eq. (14) and the extremely high electronic stability of ZrF62−with A2,obsd(ZrF6) = 2.9(2)80and A1,calc(ZrF6) ≈ 7.181allow predicting ZrF63−as electronically stable, albeit highly reactive, and unstable thermodynamically.Note that already he ZrF62−dianion was observed to be metastable unstable against the loss of an F‒with a half-life of 4 s80.

Is the VSP equation generally transferable to MCA’s? The condition for the electronic stability of an anion XQ−is

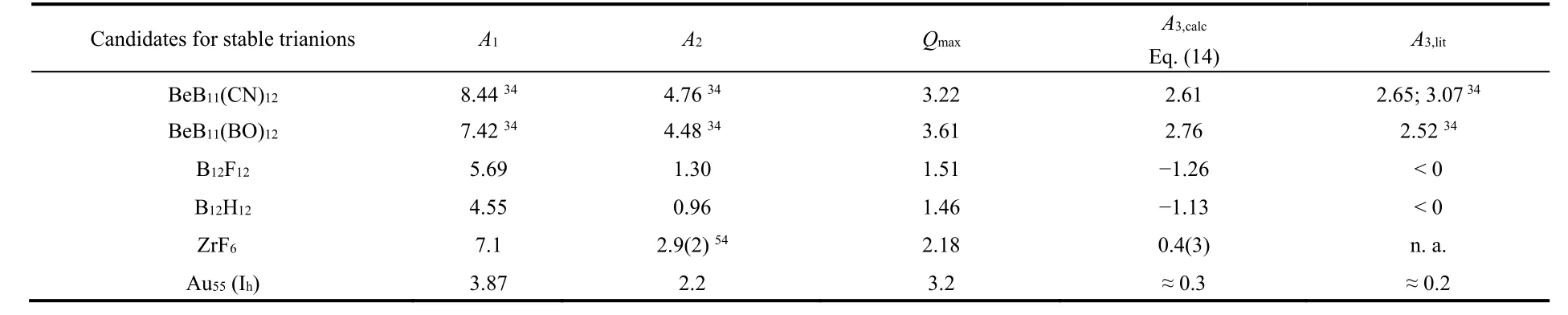
Table 2 Maximum charge acceptance beyond the anion, Q max = 1 + (12/7) A2/(A1 − A2). Calculated and literature reference values of third electron affinity, A3, calc and A3, lit, respectively. First electron affinity, A1, second electron affinity, A2, from 17, 77–79 unless indicated. Values in eV.

Estimates by Eq. (15) may be exemplified on clusters forming trianions. An electronically stable trianion, X3−, is predicted for A1＞ 2ηVS, which is equivalent to A1/I ＞ ½. Note, however, that experimental appearance sizes, nQap−, indicate electronic and thermodynamic stability, and therefore tend to be larger than the cluster sizes just referring to electronically stable MCA’s.

The experimental ionization energies and electron affinities of extended, spherical metal clusters34–36are proportional to the reciprocal cluster radius, r−1, and equivalently to n−1/3. The dependence of cluster hardness, η, as a function of n−1/3has been discussed by several groups36,37.

Extended metal clusters, such as Csnwith n ＞ 25, are candidates for trianions. The work by Assadollahzadeh et al.76on cesium clusters allows us to estimate the appearance size,,of a triply charged anionic cluster, Csn3−. These authors found simple linear dependencies of the vertical ionization potential,Iν, and electron affinity, A1,ν, on the inverse cluster size, n−1/3. In eV units the evolution of the properties is given as

Eqs. (16) and (17) have been found by constrained linear regressions, where the intercept 1.93 eV denotes the experimental work function of bulk cesium metal. Somewhat different linear regressions were obtained without this physical constraint76

Combining Eqs. (16) to (19) with Eq. (15) we obtain appearance sizes for which A1,ν(Csn)/Iν(Csn) ＞as nap3−= 29 by the constraint regression, and n ap3−= 69 by the unconstrained linear fit. On average our estimate is that cesium clusters with n ＞ 50 may form stable triply charged anions Cs3n−. Note that the electronic stability of Cs213−has been predicted in Ref. 17.

The data on [n]fullerenes, Cn, allow more confident estimates,because the experimental I and A1data for large fullerenes 78 ≤n ≤ 106, are well modelled by charged hollow spheres37,51.Accordingly I and A1are proportional to n−1/2and the slopes nearly symmetrical51. The Mulliken electronegativity becomes roughly independent of size and approximates χ0= 5.13 eV, the work function of graphene as the infinite reference system51,71.Unconstrained linear regressions without forced intercept at this work function have been performed for the [n]fullerenes, n ≥ 78,using the experimental I and A1 data of Seifert, Boltanina et al.51.The established work function value for an infinitely large fullerene, 5.13 eV, has been taken as a single point in the set of 17 experimental data points, and all data carried the same statistical weight71

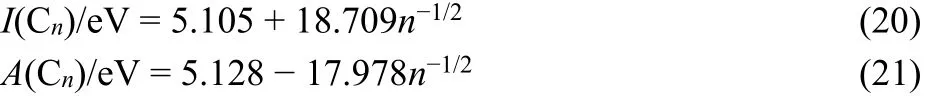
The correlation coefficients are R = 0.9941 and R = 0.9970,respectively.

The results confirm earlier statements71,82that the hardness and the electrophilicity indices of [n]fullerenes cannot be calculated by averaging atomic hardness and electrophilicity increments, respectively. The [n]fullerene hardness converges to practically zero, and the electrophilicity rises towards infinity for n → ∞. Eqs. (20) and (21) are combined with Eq. (12) to obtain

which in turn allows estimating MCA appearance sizes for large[n]fullerenes with n ＞ 80

This allows specific predictions, e.g., n3ap−＞ 138 for the[n]fullerenes. The estimates by Walsh83are 156 ＜ n3ap−＜ 192.The molecular energy is also affected by structural changes and relaxations between the neutral, anionic and MCA species. This is manifested in significant differences between the vertical and adiabatic values of I, A1and A2. In clusters up to n ≈ 40, I and A1values frequently include prominent odd-even oscillations and shell effects83,84. Modelling such important structural relaxations and complex behaviors upon electron attachment is outside the scope of the present method. However, the anionic charging in larger size metal clusters and [n]fullerenes is known to induce moderate structural changes only3,4,51,83,84. In general, the odd-even effects are “washed” out by increasing sizes34−36,51,83,84.Thus the global minimum structures of alkali metal clusters with n ＞ 55 are dominated by geometrical packing effects84.

4 Conclusions

The valence-state parabola model has been extended to higher negative charges beyond simple anions. The electronic stability of multiply charged anions, XQ‒, is quantitatively expressed as functions of two properties, A1and I, of the “ancestor” species, X, which are easier to determine. The VSP model provides a stability criterion requiring χVS(X2−) ＞ 0 and suggests A2,VS≈ A1– ηVS. A fine-tuning results in A2,calc= A1– (7/6)ηVS, and gives accurate results. The calculated third electron affinities, A3,calc,and estimates of nap3−, the appearance size of triply charged anionic clusters agree well with the literature values.

Acknowledgment:I thank Prof. Hans-Joachim Werner for continued hospitality at the Institut für Theoretische Chemie,Universität Stuttgart, and Prof. Michael C. Böhm for many helpful discussions.

(1) Pearson, R. G. Chemical Hardness; Wiley-VCH: Weinheim, Germany,1997. doi: 10.1002/3527606173

(2) Sommerfeld, T.; Weber, R. J. J. Phys. Chem. A 2011, 115, 6675.doi: 10.1021/jp202817d

(3) Walters, T.; Wang, X. B.; Wang, L. -S. Coord. Chem. Rev. 2007, 251,474. doi:10.1016/j.ccr.2006.04.010

(4) Herlert, A.; Kruckeberg, S.; Schweikhard, L.; Vogel, M.; Walther, C.Phys. Scr 1999, T80, 200.doi: 10.1238/Physica.Topical.080a00200

(5) Franzreb, K.; Wiliams, P. J. Chem. Phys. 2005, 123, 224312.doi: 10.1063/1.2136154

(6) Walsh, N.; Martinez, F.; Marx, G., Schweikhard, L., Ziegler, F.J. Chem. Phys. 2010, 132, 014308. doi:10.1063/1.3270153

(7) Wong, A. Y.; Mamas, D. L.; Arnush, D. Phys. Fluids 1975, 18, 1489.doi: 10.1063/1.861034

(8) Wang, X. B.; Wang, L. S. Photoelectron Spectroscopy of Multiply Charged Anions. In Annual Review Physical Chemistry; Annual Reviews Inc.: Palo Alto, CA, USA, 2009; Vol. 60, pp. 105–126.

(9) Langer, P.; Freiberg, W. Chem. Rev. 2004, 104, 4125.doi: 10.1021/cr010203l

(10) Tallgren, L. Acta Med. Scand. Suppl. 1980, 640, 1.

(11) Lee, A.; Dawson, P. A.; Markovich, D. Int. J. Biochem. Cell Biol.2005, 37, 1350. doi: 10.1016/j.biocel.2005.02.013

(12) Ramanathan, V.; Crutzen, P. J.; Kiehl, J. T.; Rosenfeld, D. Science 2001, 294, 2119. doi: 10.1126/science.1064034

(13) Scheller, M. K.; Compton, R. N.; Cederbaum, L. S. Science 1995,270, 1160. doi: 10.1126/science.270.5239.1160

(14) Boldyrev, A. I.; Gutowski, M.; Simons, J. Acc. Chem. Res. 1996, 29,497. doi: 10.1021/ar960147o

(15) Dreuw, A.; Cederbaum, L. S. Chem. Rev. 2002, 102, 181.doi: 10.1021/cr0104227

(16) Feuerbacher, S.; Cederbaum, L. S. J. Phys. Chem. A 2005, 109, 11401.doi: 10.1021/jp053305e

(17) von Szentpály, L. J. Phys. Chem. A 2010, 114, 10891.doi: 10.1021/jp107177d

(18) Parr, R. G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1989.

(19) Parr, R. G.; Pearson, R. G. J. Am. Chem. Soc. 1983, 105, 7512.doi: 10.1021/ja00364a005

(20) Cohen, A. J.; Mori-Sánchez, P.; Yang, W. Chem. Rev. 2012, 112, 289.doi: 10.1021/cr200107z

(21) Parr, R. G.; von Szentpály, L.; Liu, S. J. Am. Chem. Soc. 1999, 121,1922. doi: 10.1021/ja983494x

(22) Bergmann, D.; Hinze, J. Angew. Chem. Int. Ed. 1996, 35, 150; with earlier references quoted therein. doi: 10.1002/anie.199601501

(23) von Szentpály, L. J. Mol. Struct. THEOCHEM 1991, 233, 71.doi: 10.1016/0166-1280(91)85055-C

(24) von Szentpály, L. Int. J. Quantum Chem. 2000, 76, 222.doi: 10.1002/(SICI)1097-461X(2000)76:2＜222::AID-QUA11＞3.0.CO;2-6

(25) Glasser, L.; von Szentpály, L. J. Am. Chem. Soc. 2006, 128, 12314.doi: 10.1021/ja063812p

(26) Datta, D.; Shee, N. K.; von Szentpály, L. J. Phys. Chem. A 2013, 117,200. doi: 10.1021/jp3103386

(27) von Szentpály, L. J. Phys. Chem. A 2015, 119, 1715.doi: 10.1021/jp5084345

(28) Sen, K. D.; Boehm, M. C.; Schmidt, P. C. Structure and Bonding;Springer-Verlag: Berlin, Germany, 1987; Vol. 66, p. 99.

(29) Janak, J. F. Phys. Rev. B 1978, 18, 7165.doi: 10.1103/PhysRevB.18.7165

(30) Jensen, F. J. Chem. Theory Comput. 2010, 6, 2736.doi: 10.1021/ct1003548

(31) Kim, M. -C.; Sim, E.; Burke, K. J. Chem. Phys. 2011, 134, 171103.doi: 10.1063/1.3590364

(32) Wade, K. Chem. Commun. 1971, 792. doi: 10.1039/c29710000792

(33) Mingos, D. M. P. Acc. Chem. Res. 1984, 17, 311.doi: 10.1021/ar00105a003

(34) Zhao, T.; Zhou, J.; Wang, Q.; Jena, P. Angew. Chem. Int. Ed. 2017, 56,13421. doi: 10.1002/anie.201706764.

(35) Herlert, A.; Schweighardt, L. Int. J. Mass Spectrom. 2003, 229, 19.doi: 10.1016/S1387-3806(03)00251-3

(36) Yannouleas, C.; Landman, U. Chem. Phys. Lett. 1993, 210, 437.doi: 10.1016/0009-2614(93)87050-D

(37) de Heer, W. A. Rev. Mod. Phys. 1993, 65, 611.doi: 10.1103/RevModPhys.65.611

(38) Gutsev, G. L. Chem. Phys. Lett. 1991, 184, 305.doi: 10.1016/0009-2614(91)85128-J

(39) Pernpointner, M.; Cederbaum, L. S. J. Chem. Phys. 2007, 126,144310. doi: 10.1063/1.2721531

(40) Wesendrup, R.; Schwerdtfeger, P. Inorg. Chem. 2001, 40, 3351.doi: 10.1021/ic010169t

(41) Craciun, R.; Picone, D.; Long, R. T.; Li, S.; Dixon, D. A.;Peterson, K. A.; Christe, K. O. Inorg. Chem. 2010, 49, 1056.doi: 10.1021/ic901967h

(42) Craciun, R.; Long, R. T.; Dixon, D. A.; Christe, K. O. J. Phys. Chem.A 2010, 114, 7571. doi: 10.1021/jp1022949

(43) Macgregor, S.A.; Moock, K. H. Inorg. Chem. 1998, 37, 3284.doi: 10.1021/ic9605736

(44) Seppelt, K. Chem. Rev. 2015, 115, 1296. doi: 10.1021/cr5001783

(45) Pradhan, K.; Gutsev, G. L.; Weatherford, C. A.; Jena, P. J. Chem.Phys. 2011, 134, 144305. doi: 10.1063/1.3570578

(46) Uzunova, E. L. J. Phys. Chem. A 2011, 115, 10665.doi: 10.1021/jp2034888

(47) Zhou, M.; Andrews, L.; Ismail, N.; Marsden, C. J. Phys. Chem.2000, 104, 5495. doi: 10.1021/jp000292q

(48) Zein, S.; Ortiz, J. V. J. Chem. Phys. 2011, 135, 164307.doi: 10.1063/1.3636082

(49) Zein, S.; Ortiz, J. V. J. Chem. Phys. 2012, 136, 224305.doi: 10.1063/1.4728073

(50) Anusiewicz, I.; Freza, S.; Sikorska, C.; Skurski, P. Chem. Phys. Lett.2010, 493, 234. doi: 10.1016/j.cplett.2010.05.058

(51) Boltanina, O. V.; Ioffé, I. N.; Sidorov, L. N.; Seifert, G.; Vietze, K.J. Am. Chem. Soc. 2000, 122, 9745. doi: 10.1021/ja000734b

(52) Hampe, O.; Neumaier, M.; Blom, M. N.; Kappes, M. M. Chem. Phys.Lett. 2002, 354, 303. doi: 10.1016/S0009-2614(02)00124-0

(53) Wang, X. -B.; Woo, H. -K.; Yang, J.; Kappes, M. M.; Wang, L. -S.J. Phys. Chem. C 2007, 111, 17684. doi: 10.1021/jp0703861

(54) Wang, X. -B.; Woo, H. -K.; Huang, X.; Kappes, M. M.; Wang, L. -S.Phys. Rev. Lett. 2006, 96, 143002.doi: 10.1103/PhysRevLett.96.143002

(55) Nasibullaev, S. K.; Davletbaeva, G. D.; Vasil’ev, Z. V.; Nasibullayev,I. S. Fuller. Nanotub. Carbon Nanostruct. 2004, 12, 491.doi: 10.1081/FST-120027212

(56) Wang, X. -B.; Chi, C.; Zhou, M.; Kuvychko, I. V.; Seppelt, K.;Popov, A. A.; Strauss, S. H., Boltalina, O.; Wang, L. -S. J. Phys.Chem. A 2010, 114, 1756. doi: 10.1021/jp9097364

(57) Caddeo, C.; Malloci, G.; De Angelis, F.; Colombo, L.; Mattoni, A.Phys. Chem. Chem. Phys. 2012, 14, 14293. doi: 10.1039/c2cp42037f

(58) Belau, L.; Wheeler, S. W.; Ticknor, B. W.; Ahmed, M.; Leone, S. R.;Allen, W. D., Schaefer, H. F.; Duncan, M. A. J. Am. Chem. Soc. 2007,129, 10229. doi: 10.1021/ja072526q

(59) Ortíz, J. V.; Zakrzewski, V. G. J. Chem. Phys. 1994, 100, 6614.doi: 10.1063/1.467071

(60) Ortíz, J. V.; Zakrzewski, V. G. J. Chem. Phys. 1995, 102, 294.doi: 10.1063/1.469402

(61) Sommerfeld, T. J. Phys. Chem. A 2000, 104, 8806.doi: 10.1021/jp0017590

(62) Wang, J.; Yang, M.; Jellinek, J.; Wang, G. Phys. Rev. 2006, A74,023202. doi: 10.1103/PhysRevA.74.023202

(63) Kostko, O. Photoelectron Spectroscopy of Mass-selected Sodium,Coinage Metal and Divalent Metal Cluster Anions; Ph. D. Thesis,Universität Freiburg: Freiburg, Germany, 2007.www.freidok.uni-freiburg.de

(64) Yannouleas, C.; Landman, U. Phys. Rev. B 2000, 61, R10587.doi: 10.1103/PhysRevB.61.15895

(65) Berkowitz, J.; Lifshitz, G. J. Chem. Phys. 1968, 48, 4346.doi: 10.1063/1.1667997

(66) Jin, Y.; Maroulis, G.; Kuang, X.; Ding, L.; Lu, C.; Wang, J.; Lv, J.;Zhang, C.; Ju, M. Phys. Chem. Chem. Phys. 2015, 17, 13590.doi: 10.1039/c5cp00728c

(67) Zakrzewski, V. C.; von Niessen, W. Theor. Chim. Acta 1994, 88, 75.doi: 10.1007/BF01113735

(68) Berghof, V; Sommerfeld, T; Cederbaum, L. S. J. Phys. Chem. A 1998, 102, 5100. doi: 10.1021/jp9808375

(69) Kaplan, I. G.; Dolgounitcheva, O.; Watts, J. D.; Ortiz, J. V. J. Chem.Phys. 2002, 117, 3687. doi: 10.1063/1.1494801

(70) Roy, D. R.; Chattaraj, P. K. J. Phys. Chem. A 2008, 112, 1612.doi: 10.1021/jp710820c

(71) von Szentpály, L. J. Mol. Model 2017, 23, 217.doi: 10.1007/s00894-017-3383-z

(72) Sabzyan, H.; Noorisafa, Z.; Keshavarz, E. Spectrochim. Acta A 2014,117, 95. doi: 10.1016/j.saa.2013.07.111

(73) Zakrzewski, V. G.; Dolgounitcheva, O.; Ortiz, J. V. J. Chem. Phys.1996, 105, 5872. doi: 10.1063/1.472428

(74) Zhu, G. -Z. Wang, L. -S. J. Chem. Phys. 2015, 143, 221102.doi: 10.1063/1.4937761

(75) Nielsen, S. B.; Nielsen, M. B. J. Chem. Phys. 2003, 119, 10069.doi: 10.1063/1.1618216

(76) Assadollahzadeh, B.; Thierfelder, C.; Schwerdtfeger, P. Phys. Rev. B 2008, 78, 245423. doi: 10.1103/PhysRevB.78.245423

(77) Haynes, W. M.; Lide, R. D. Handbook of Chemistry and Physics, 92nd ed.; CRC Press: Boca Raton, FL, USA, 2011–2012.

(78) Lias, S. G.; Bartmess, J. E.; Liebman, J. F.; Holmes, J. L.; Levin, R.D.; Mallard, W. G. Ion Energetics Data in NIST Chemistry Webbook;NIST Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, Maryland, USA, 2015.

(79) Richard, R. M.; Marshall, M. S.; Dolgounitcheva, O.; Ortiz, J. V.;Brédas, J. -L.; Marom, N.; Sherrill, C. D. J. Chem. Theory Comput.2016, 12, 595. doi: 10.1021/acs.jctc.5b00875

(80) Wang, X. B.; Wang, L. -S. J. Phys. Chem. A 2000, 104, 4429.doi: 10.1021/jp000362t

(81) Gutsev, G. L.; Boldyrev, A. I. Mol. Phys. 1984, 53, 23.doi: 10.1080/00268978400102111

(82) von Szentpály, L. J. Phys. Chem. A 2011, 115, 8528.doi: 10.1021/jp203319y

(83) Walsh, N. Multiply-Negatively Charged Aluminum Clusters and Fullerenes; Ph. D. Thesis, Universität Greifswald, Greifswald,Germany, 2008. ub-ed.ub.unigreifswald.de/opus/volltexte/2008/.../Diss_Walsh.pdf

(84) Taylor, K. J.; Pettiette-Hall, C. L.; Chesnovsky, O.; Smalley, R. E.J. Chem. Phys. 1992, 96, 3319. doi: 10.1063/1.461927