Thermodynamic Dual Descriptor

FRANCO-PÉREZ Marco , GÁZQUEZ José L. , AYERS Paul W. , VELA Alberto

1 Departamento de Química, Universidad Autónoma Metropolitana-Iztapalapa, Av. San Rafael Atlixco 186, Ciudad de México, 09340,México.

2 Department of Chemistry, McMaster University, Hamilton, Ontario, L8S 4M1, Canada.

3 Departamento de Química, Centro de Investigación y de Estudios Avanzados, Av. Instituto Politécnico Nacional 2508,Ciudad de México, 07360, México.

1 Introduction

One of the most important tasks in chemistry is to establish new rules, concepts and principles adequate to enhance the understanding of the reactivity of chemical species. In recent decades, the description of chemical reactivity in density functional theory (CR-DFT) has provided theoretical support to some of these concepts and rules, which were previously elucidated, intuitively, by empirical observations1–7. The chemical potential1,8(μ) which is equal to minus the electronegativity8–10(χ), and the chemical hardness11–16(η) constitute important examples, together with the Fukui function17–19(f(r)) and the dual descriptor20,21(Δf(r)). The first two, μ and η, have been identified with the first and second derivatives of the energy with respect to the number of electrons (N) at constant external potential (v(r)). Thus if one makes use of a smooth quadratic interpolation between the energies of the N0 − 1, N0 and N0 + 1 electron systems (N0is an integer) one finds that13

and

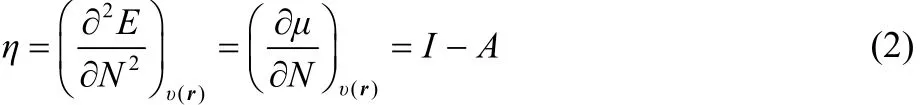
where I = EN0−1− EN0and A = EN0− EN0+1are the vertical first ionization potential and electron affinity, respectively, relative to the species with N0electrons.

In the case of f(r) and Δf(r), these local reactivity descriptors have been defined as the first and second derivatives of the electron density with respect to the number of electrons, and if one also makes use of a smooth quadratic interpolation between the densities of the N0– 1, N0and N0+ 1 electron systems, one finds that

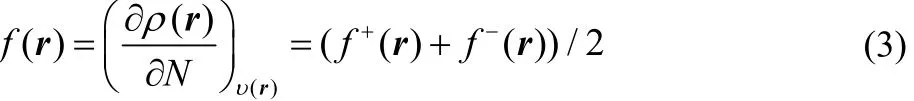
and

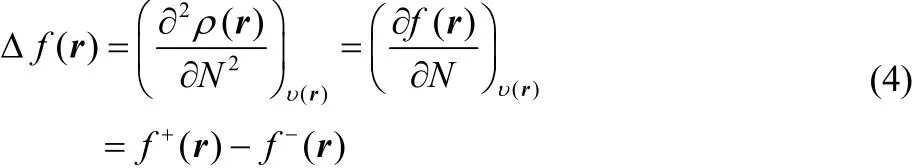
where f+= ρN0+1(r) − ρN0(r) and f−(r) = ρN0(r) − ρN0−1(r)correspond to the Fukui functions for nucleophilic and electrophilic attacks, respectively17.

These relationships (Eqs. (1)–(4)) have been very useful to understand many aspects of chemical interactions at the global level with μ and η, and at the local level with f (r) and Δf (r). In particular, it is worth to mention that the dual descriptor as expressed in Eq. (4) has proven to be a very useful tool not only in the characterization of the regioselectivity of a broad amount of chemical systems but also, to reveal the amphiphilic features of atoms and molecules22–37. A positive value of the dual descriptor in a given point in the tridimensional molecular space indicates that such point is susceptible to undergo through a nucleophilic attack, while a negative value indicates that such point is susceptible to undergo through an electrophilic attack. In the special case when the dual descriptor equals zero, a molecular species will not exhibit any preference to react as a nucleophile or as electrophile.

However, it has been demonstrated, using a three state gran canonical ensemble composed by the N0− 1, N0and N0+ 1 electron systems, that at a temperature of 0 K, the energy and the density are given by a series of straight lines connecting the integer values of the number of electrons38,39. Later Yang,Zhang and Ayers40reach the same result without invoking ensembles, showing that this result is general. This situation implies that the left and right derivatives of the energy and of the density are different, that is

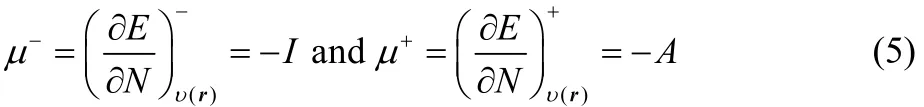
and

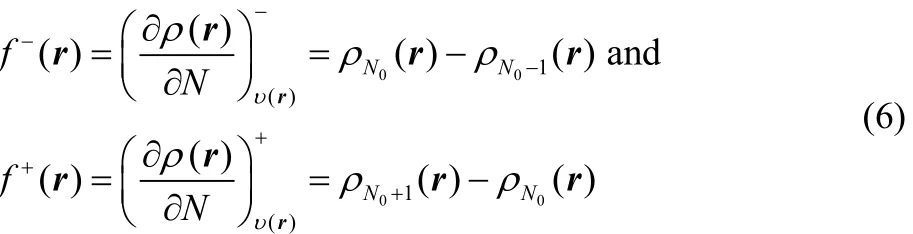
while the second derivatives are given by41

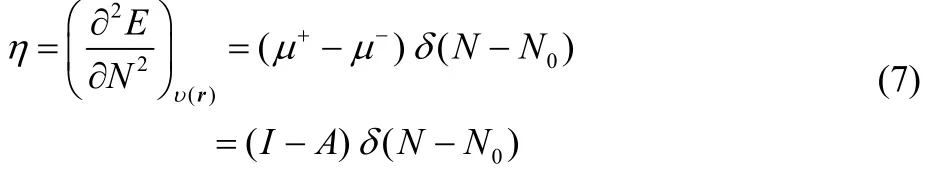
and

Thus, the presence of the Dirac delta function in Eqs. (7) and(8) implies that these definitions of the chemical hardness and the dual descriptor are not appropriate for the analysis of chemical reactivity. One way to overcome this situation is to make use of the smooth quadratic interpolation that leads to Eqs. (2) and (4). However, recently, it has been established that smooth interpolations between integer number of electrons can not be represented in terms of grand canonical ensembles42,and it may present inconsistencies43. This situation indicates that it would be desirable to establish alternative definitions of the chemical hardness and the dual descriptor whose basic electronic contribution could be given by Eqs. (2) and (4),because it has been through these definitions that it has been possible to analyze at the global and local levels many important aspects of a wide variety of chemical interactions1–7,16,20,21,44,45.

In recent reports46–61, it has been shown that very important aspects regarding the chemical reactivity of the species can be revealed if one introduces the temperature as a free variable in the CR-DFT, a generalization that has been denominated as the temperature dependent chemical reactivity theory or τ-CRT.The mathematical framework of the τ-CRT is the grand canonical ensemble (GCE), together with the grand canonical potential (GCP) expressed as a unique functional of the equilibrium electron density1,62,63. One of the most important features of this framework is that atoms and molecules are naturally considered as open quantum systems able to exchange energy and electrons with surroundings and it is thus adequate to study how chemical species interact with external agents.Using the τ-CRT framework it has been possible to determine the exact (average) energy and the exact (average) density as a function of the (average) number of electrons, at any temperature, allowing us to establish exact generalizations for important CR-DFT chemical reactivity descriptors, as the electronic chemical potential8and the Fukui function17, to the temperature dependent situation48,49. Moreover, using the τ-CRT formalism we have recently56suggested that a maximum hardness principle14,64is strongly coupled with a minimum electronic fractional charge principle developed by Chattaraj, Cedillo and Parr65, indicating that the most stable chemical species are those that have an integer (average)number of electrons, or more explicitly, species with a fractional amount of electrons always tend to react with an external agent or to evolve towards the next most stable integer electrons number thermodynamic state56,58.

The analysis of the maximum hardness principle just mentioned was done by introducing a new definition of hardness based on the GCE, called the thermodynamic hardness, that retains the essential features of the Parr and Pearson hardness (Eq. (2)), without the use of a smooth interpolation, but it avoids the Dirac delta function. The object of the present work is to perform a similar analysis for the dual descriptor.

2 Theoretical framework

2.1 The temperature dependent chemical reactivity theory formalism.

In the GCE formulation, any equilibrium thermodynamic state is fully determined once the temperature T, the external potential υ(r) and the chemical potential of the reservoir μBathhave well-defined values66,67. The relationship between this GC free variables and the equilibrium electron density was formally demonstrated by Mermin and properly reformulated by Kohn and Vashishta1,62,63. At a given temperature T and modified potential u(r) = υ(r) − μBath, the grand potential is a unique functional of the equilibrium electron density ＜ρ(r)＞,

where E[＜ρ(r)＞], ST[＜ρ(r)＞] and N[＜ρ(r)＞] are density functionals for the average electronic energy, the entropy and the average number of electrons, respectively (see48for detailed definitions of these quantities), while,

where,

and

are the density and the grand canonical density operators,respectively. In Eq. (11) the sum runs over the N electrons that constitute the electronic system, while in Eq. (12) ˆN represents the electron-number operator, ˆH is the Hamiltonian, β =1/kBT, and the trace (tr) is over all the electronic (ground and excited) states consistent with the external potential under consideration (including the continuum).

The GCP electron density in Eq. (10) has the following integration property,

where N0is a reference integer number of electrons, and −1 ≤ω[＜ρ(r)＞] ≤ 1 is the fractional part of the electron number. Eq.(13) constitutes one of the most important features of the GCE formalism, since systems exhibiting a fractional amount of electronic charge appear naturally as a consequence of the particular values of the GCE free variables T, υ(r) and μBath.

In practice one cannot handle the full set of possible electronic states and the size of our ensemble must be delimitated. It is known that the ensemble model constituted by the three contiguous fundamental electronic states, ψN0, ψN0+1 and ψN0−1, reliably captures the reactivity features of substances at temperatures of chemical interest57. For this ensemble model, the equilibrium electron density and the fractional charge appearing in Eqs. (10) and (13) respectively, are expressed as follows48,49,

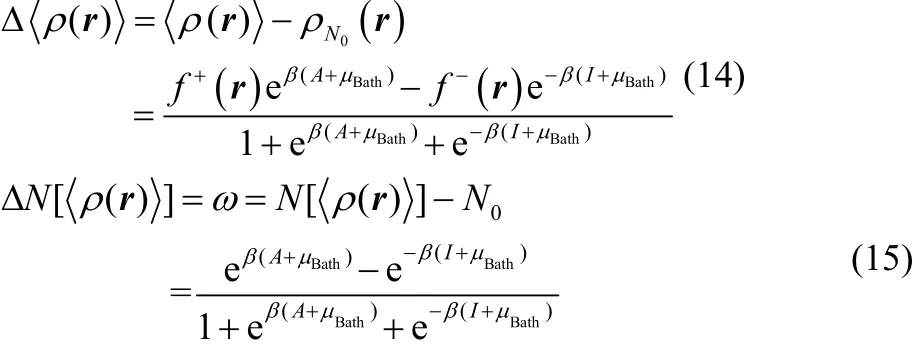
It can be easily corroborated that Eq. (15) is bounded between−1 ≤ ω ≤ 1, while Eq. (14) between –f−(r) ≤Δ＜ρ(r)＞ ≤ f+(r).

To obtain a density expression that explicitly depends on the fractional charge ω, one must obtain first an expression for μbathfrom Eq. (15), that leads to the following two roots49,

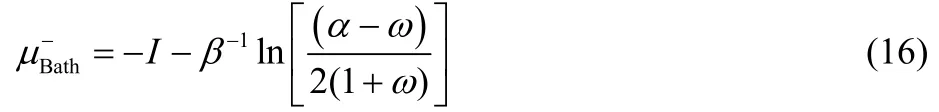
and

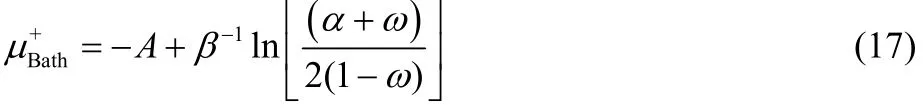
where,

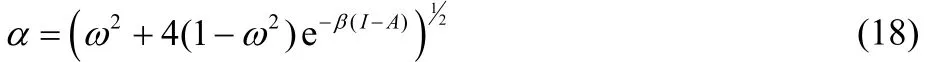
Eqs. (16) and (17) provide results only for non-positive and non-negative values of ω, respectively, and consequently, both equations are needed in order to describe the chemical potential of the bath over the full range of fractional charge and temperature values. Eqs. (16) and (17) can be equivalently expressed as,

and

Inserting Eqs. (19) and (20) into Eq. (14) and after some algebraic manipulations one finally gets,

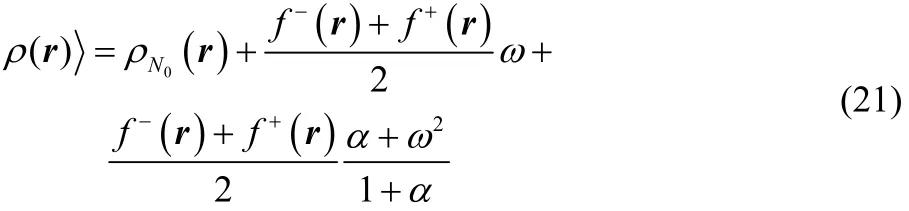
Eq. (21) provides the exact dependence of the equilibrium electron density with respect to the average number of electrons(fractional charge), valid for the three states ensemble model under consideration at any temperature (even in the zero temperature limit).

Through a similar strategy, we have also reported the exact average electronic energy dependence with respect to the number of electrons68,

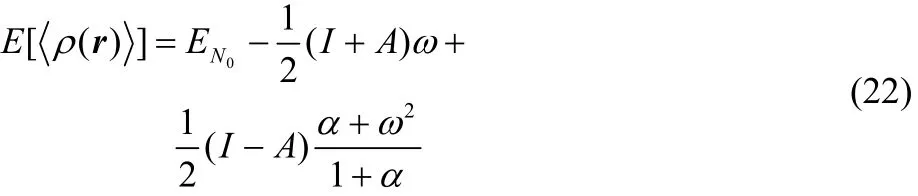
showing that Eq. (22) is a continuous and infinitely differentiable function (this feature is provided by the α quantity) in the average number of electrons (fractional charge). Evidently, these important results can be extended to the average electron density expression given in Eq. (21).

2.2 Temperature dependent local chemical reactivity descriptors from the equilibrium electron density

Given the local (spatial dependent) nature of the equilibrium electron density, it is possible to get insights about the regioselectivity features of a chemical species by removing one of the three GCE thermodynamic constraints, allowing our system to interact with the surroundings. Therefore, there are three possible kinds of interactions in the GCE framework,either by exchanging electrons or energy with the reservoir, or by modifying the external potential generated by the nuclei,which is often associated with an infinitesimal variation in the molecular geometry (although other external potential perturbations might also be considered). Electrons transfer is one of the most important phenomena in a chemical process and constitutes the main focus in this study.

In the GCE formalism, the responses of a chemical system towards the donation and the acceptation of a certain amount of electronic charge may be determined through two different strategies. At first instance, one must recall that in the GCE framework, the chemical potential of the reservoir, μBath, is a free variable and if the temperature and the external potential are kept constant, it modulates the amount of the average number electrons exhibited by an electronic species at a given equilibrium state. Thus, one may quantify the response of the electron density towards electron transfer using the local softness69,70, which is defined as the partial derivative of the equilibrium electron density with respect to μBath, keeping constant the temperature and the external potential,

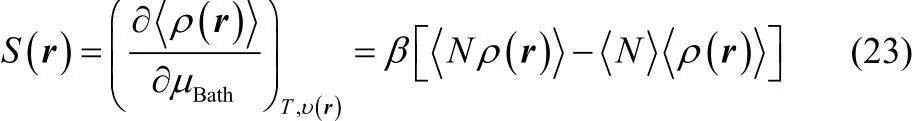
where the term inside square brackets are the thermal fluctuations between the average electrons number and the equilibrium electron density.

The main inconvenient of the local softness given in Eq.(23), is that it behaves as a Dirac delta function in μBathas the temperature approaches zero, and is thus not suitable for chemical reactivity analysis purposes48. In the second strategy one directly performs partial derivatives of the equilibrium electron density with respect to the average number of electrons, that corresponds to the finite temperature definition of the electronic Fukui function48,

which can be expressed, according to the following chain rule,as

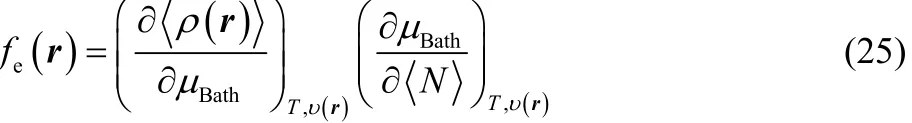
where the first derivative in the right-hand side of Eq. (25) is given by Eq. (23), while

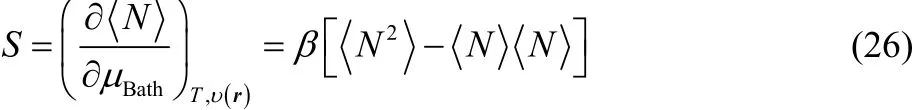
is the thermodynamic softness65,69and therefore,

It is interesting to note that as the local softness, the thermodynamic softness given in Eq. (26) also behaves as a Dirac delta function in μBath as the temperature approaches zero.However, if one considers the ratio of this two fluctuating quantities (Eqs. (23) and (26)), the Dirac delta behavior cancels out, leading to a well-behaved chemical reactivity descriptor, the electronic Fukui function. In the case of the three states ensemble model mentioned above, the electronic Fukui function in Eq. (27)can be compactly expressed as (one may corroborate that the same result is obtained if one performs the partial derivative of Eq. (21) with respect to the fractional charge ω),

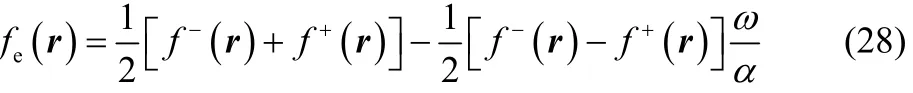
where ω and α are given by Eqs. (15) and (18), respectively.For any temperature value of chemical interest, Eq. (28)displays the following three possible results,

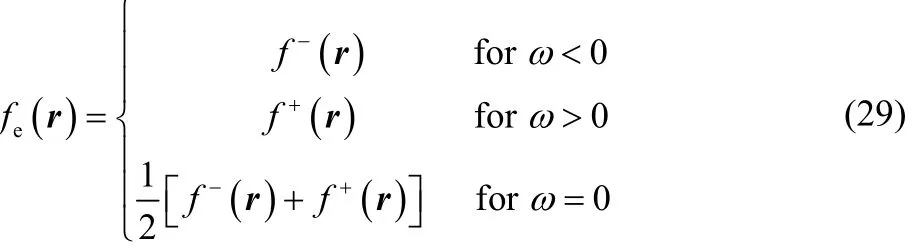
recovering thus the well-known zero-temperature working equations for the Fukui function17,18.

As mentioned in the precedent section, the equilibrium electron density given in Eq. (21) is infinitely differentiable with respect to the average number of electrons and is therefore suitable to formulate higher order reactivity descriptors. Taking the second order partial derivative of Eq. (21) with respect to the average number of electrons, we get the finite temperature generalization of the dual descriptor20,21,44,

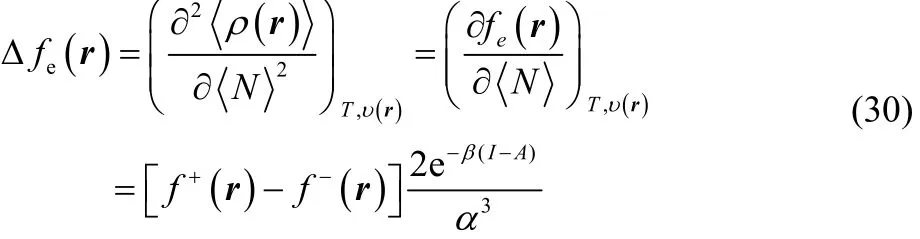
which is known as the electronic dual descriptor48. The term in square brackets at the right-hand side of the third equality in Eq. (30) is precisely the dual descriptor obtained by using the smooth quadratic interpolation (Eq. (4)). However, one can prove that the term outside the square brackets resembles a Dirac delta function in the fractional charge ω (or equivalently in the average number of electrons) as the temperature approaches zero, making Eq. (30) not suitable to describe the chemical reactivity of a species at the local level. In fact, this function becomes exactly equal to the Dirac delta function at T = 0, leading to Eq. (7).

3 Theoretical development

3.1 The thermodynamic dual descriptor

The Dirac delta behavior exhibited by the finite temperature dual descriptor in Eq. (30) is basically due to the fact that when the temperature tends to 0 K, and even at temperatures of chemical interest, like room temperature, the electronic Fukui function given by Eq. (27) reduces to the expression given in Eq. (29), which can be interpreted as a Heaviside step function in the fractional charge ω, and therefore, when taking the derivative of Eq. (28) with respect to ＜N＞, or ω = ＜N＞ − N0, to obtain Eq. (30), one is taking the derivative of a Heaviside step function, which leads to the Dirac delta function.

The definition of the dual descriptor as the second derivative of the average electron density with respect to ＜N＞, or alternatively, the first derivative of the electronic Fukui function with respect to ＜N＞, implies that the definition of the electronic dual descriptor given in Eq. (30), actually captures the response of the Fukui function fe(r) to changes in the number of electrons. As mentioned in the precedent section,there are two strategies to compute the response of an ensemble property in relation with an electron transfer process, one is to take derivatives with respect to the number of electrons, which in the case of the electronic Fukui function, leads to the Dirac delta result (the electronic dual descriptor in Eq. (30)), while the other one, is to consider the partial derivative of the electronic Fukui function but with respect to a GCE free variable, the chemical potential of the reservoir, since, as mentioned above, any variation of μBath will modify the equilibrium value of the average number of electrons through an electron flux from or to the surroundings. In this context,one may get a new alternative definition for the dual descriptor,which we will call the thermodynamic dual descriptor56,

which captures essentially the same physical process (second order response of the average electron density with respect to an exchange of electrons) as Δfe(r). The subscript T in ΔfT(r) is used to indicate that through Eq. (31) one defines a“thermodynamic dual descriptor”, which is different from the electronic dual descriptor Δfe(r) defined through Eq. (30).

By making use of the chain rule, one can express Eq. (31) in the form,

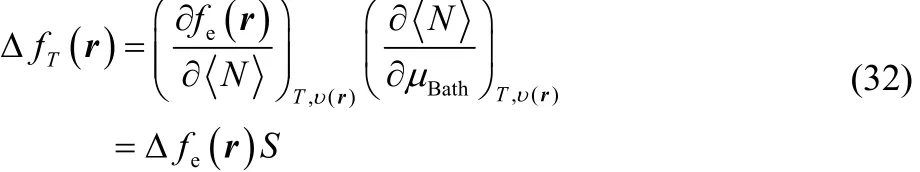
where it can be observed that our definition of thermodynamic dual descriptor is expressed as the product of two quantities that behave as a Dirac delta function but in conjugated variables, in μBathfor thermodynamic softness S, and in ＜N＞ for the electronic dual descriptor Δfe(r). Likewise, using a Maxwell type of relation,

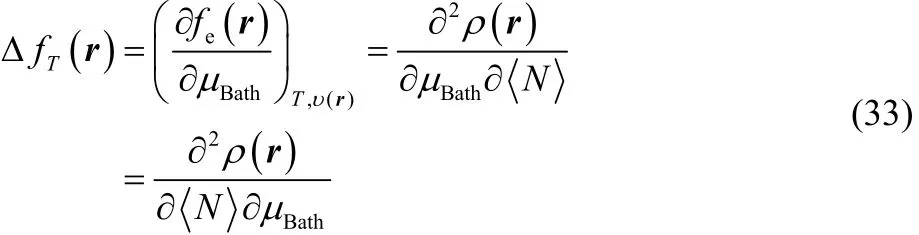
and comparing with Eq. (23), it is easy to see that,

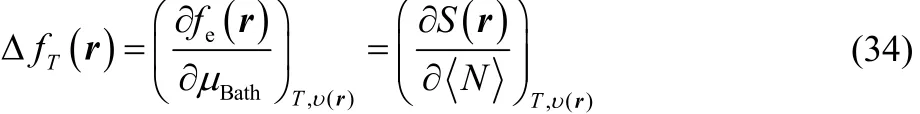
that is, our definition of thermodynamic dual descriptor contains information regarding the response of the local softness or the electronic Fukui function, towards and electron transfer process, i.e., the variation of the electronic Fukui function with respect the chemical potential of the reservoir is equivalent to the response of the local softness to variations in the average number of electrons.

In order to evaluate the partial derivatives in the right-hand side of Eq. (32) we will consider the chemically reliable three states ensemble model mentioned above. The thermodynamic softness for this ensemble model is given by49,68,

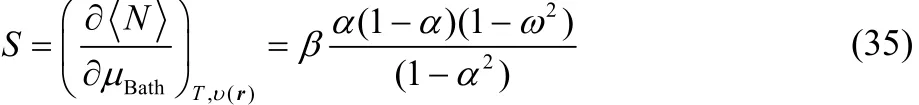
Combining Eq. (30) with Eq. (35) one obtains,

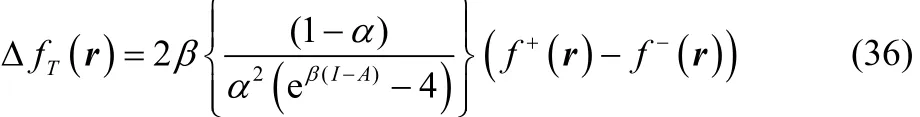
After some algebraic manipulations, Eq. (36) can be rewritten as,

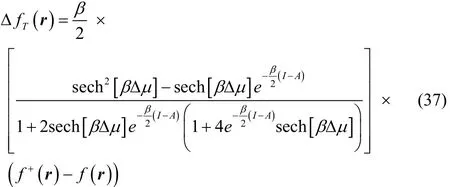
where Δ μ = μBath+ ( I + A)/2.

To get a better understanding of the values of this property,we analyze some limiting conditions. At first instance, given that the hyperbolic secant function is equal to one at Δμ = 0,then Eq. (37) becomes in this case

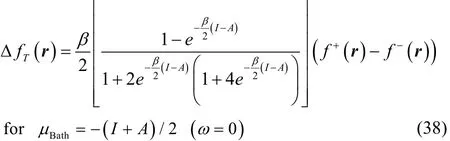
which for T ≠ 0 in the low temperature regime (up to temperatures of chemical interest) reduces to the simpler result,

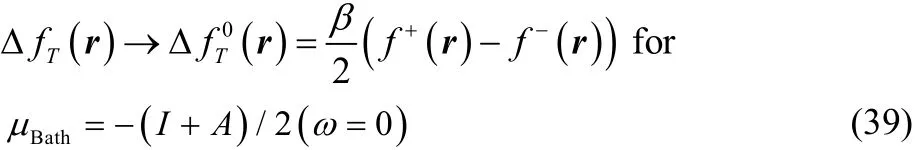
On the other hand, when Δμ ≠ 0 all the terms within the square brackets in Eq. (37) become very small, so that in the low temperature regime (up to temperatures of chemical interest) this expression can be written as

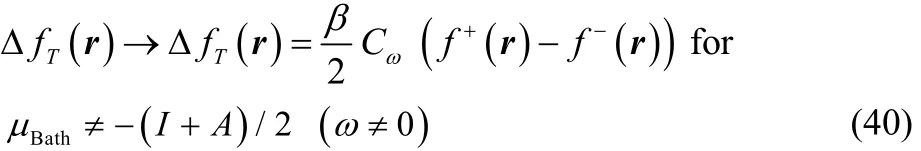
where Cω＞ 0 is very close to zero for T ≠ 0. Although it becomes exactly equal to zero at T = 0, because the terms in square brackets in Eq. (37) decay to zero faster than T. It is important to mention that the results in Eqs. (39) and (40) were obtained by setting first Δμ = 0 or Δμ ≠ 0 in Eq. (37) and taking afterwards the limit when T → 0.

Thus, the first important result to emphasize is that according to this expression, Eq. (37), the thermodynamic dual descriptor thus obtained has the form (β/2)C[f+(r) − f−(r)], where C (the term in square brackets in Eq. (37)) is a quantity that depends on the temperature and on global electronic properties of the molecule (I and A). That is, the local terms, which are the ones that contain the regioselectivity information, are equal to those of the dual descriptor given by Eq. (4), so that ΔfT(r) has the same regioselectivity information than Δf (r), but scaled by the value of the quantity (β/2)C. This situation implies that the definition of the thermodynamic dual descriptor given by Eq.(31) is equivalent to the definition given in Eq. (30), but avoids the Dirac delta function behavior at low temperatures (up to temperatures of chemical interest), without the use of a smooth interpolation.

On the other hand, one may observe from Eqs. (39) and (40)that the scaling quantity C shows important differences for systems with an average integer number of electrons (ω = 0),than those displaying fractional amounts of electronic charge(ω ≠ 0) . In the first case C = 1, as can be seen from Eq. (39), in the second case C = Cω ＞ 0, but very close to zero, Eq. (40),leading to values that are practically zero, but different from zero, at low temperatures and up to temperatures of chemical interest. However, despite these big differences in the value of C the character of the different sites for nucleophilic or electrophilic attacks, ΔfT(r) ≥ 0 or ΔfT(r) ≤ 0, respectively, will be the same as those of the dual descriptor (Eq. (4)) at any temperature. That is, even if the values at the different positions within the molecule are all very small, the regions with positive and negative values, and the relative values for the different sites will be the same as those of the dual descriptor in both cases ω = 0 or ω ≠ 0, at any temperature. This situation implies that the regioselectivity information contained in the dual descriptor of Eq. (4) is never lost, at any temperature different from zero. At T = 0, in the case of systems with fractional charge Cω= 0 and the thermodynamic dual descriptor is exactly equal to zero, while in the case of systems with zero fractional charge the thermodynamic dual descriptor diverges as(1/2kB/T), according to Eq. (39).

As mentioned in the introduction section, recently, we have also proposed an alternative definition of hardness, namely the thermodynamic hardness56, defined as the partial derivative of the electronic chemical potential with respect to variations on the thermodynamic chemical potential of the reservoir,

that leads to the expression

where, as previously mentioned, C is the term in square brackets in Eq. (37).

This definition of hardness recovers the Parr and Pearson original approximation, (Eq. (2)), without the use of a smooth interpolation, and it also avoids the Dirac delta behavior exhibited by the standard definition (partial derivative of the electronic chemical potential with respect to the average number of electrons), Eq. (7). The thermodynamic hardness has the following behavior with respect to the fractional occupancy,

where, as previously established, Cω ＞ 0 is very close to zero,so that ηT≈ 0.

The relationships given in this expression indicate that the most stable chemical systems are those that display an integer value in the average number of electrons while the maximum reactivity is achieved for systems with fractional electron charge. When coupled together, the thermodynamic hardness and the minimum softness principle65indicates that any chemical system able to exchange electrons with the surroundings will tend to exchange the excess or deficiency of fractional charge and evolve towards the next most stable average integer electron number thermodynamic state.

If one rationalizes the results obtained for the thermodynamic dual descriptor conjunctly with the thermodynamic hardness, one can infer important features. In both cases, according to Eqs. (37) and (42), one is multiplying the original definitions based on the smooth quadratic interpolation, Eq. (2) for the hardness and Eq. (4) for the dual descriptor, by the same quantity, (β/2)C. However, in the case of the thermodynamic hardness, the quantity (I − A) is a global“positive” quantity that does not depend on the position within the molecule, so that the product (β/2)C(I − A) is a global positive quantity that characterizes the molecules as a whole.Thus, in this case the large difference between the values of C for ω = 0 or ω ≠ 0, lead directly to large differences in the thermodynamic hardness of systems with an integer average number of electrons, with respect to those with fractional charge. For the latter, one may consider that their thermodynamic hardness is zero. On the other hand, for the thermodynamic dual descriptor the product (β/2)C(f+(r) − f−(r))has a global and a local component. The latter is the one that comprises the information on the regioselectivity features contained in the dual descriptor and whatever the value of C,large or small, the signs and the relative values at every point in space will be preserved for ω = 0 or ω ≠ 0, at any temperature different from zero.

3.2 The electronic Fukui function dependence with respect to the bath parameters

In this last section we want to explore the role of the thermodynamic dual descriptor in the overall chemical reactivity of a species within the GCE formalism. To do it we write the exact differential of the electronic Fukui function in terms of the grand canonical bath parameters,

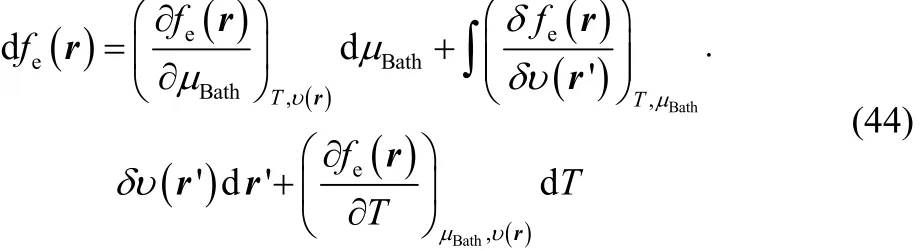
where the first derivative at the right hand side of Eq. (44)corresponds to our definition of thermodynamic dual descriptor. For the second derivative we use the identity,

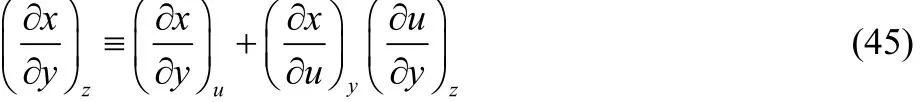
to obtain

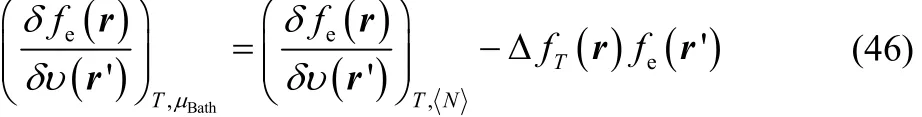
where we have used Eq. (32). The functional derivative at the right-hand side of Eq. (46) can be equivalently expressed as follows,

where χe(r, r’) is the linear response density function70–74.Introducing Eqs. (46) and (47) in Eq. (44) one finally finds that

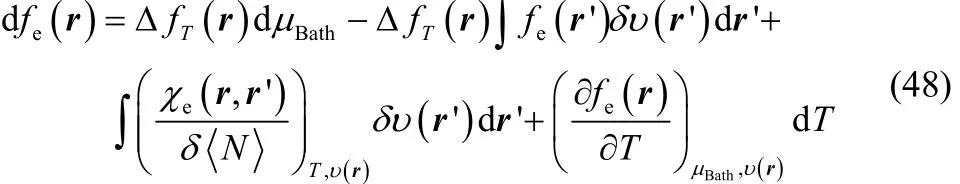
This relationship confirms ΔfT(r) to be the corresponding response coefficient of fe(r) with respect to μBath, but furthermore, from this exact differential one can observe that the response of the electronic Fukui function with respect to perturbations on the external potential can be split into two contributions. The first one, which contains our definition of thermodynamic dual descriptor times the electronic Fukui function (second term in Eq. (48)) and the second one (third term in Eq. (48)) the variation of the linear response density function with respect to the number of electrons, which appears as a response coefficient.

4 Conclusions

In this work we have made use of the GCE mathematical framework to develop a new definition of the dual descriptor,the thermodynamic dual descriptor, which is given by the crossed second order derivative of the average electron density with respect the average number of electrons and with respect to the chemical potential of the electrons reservoir, or equivalently given by the first order derivative of the electronic Fukui function with respect to the chemical potential of the electrons reservoir. Since the chemical potential of the electrons reservoir control the average number of electrons in the GCE,the derivatives with respect to it retain similar physical features as those that arise from the derivative with respect to the average number of electrons, avoiding in this way the Dirac delta behavior observed in the “exact” definition of the standard dual descriptor (second order partial derivative of the average electron density with respect the average number of electrons).

It is pertinent to remark that since in the GCE formalism, any variation of the chemical potential of the reservoir leads to an electrons transfer, the thermodynamic dual descriptor keeps the same philosophy than the original dual descriptor, Eq. (4), that is, a second order (local) chemical reactivity descriptor related with electrons transfer.

In fact, the results obtained show that the thermodynamic dual descriptor contains the same regioselectivity information that the one contained in the dual descriptor based on the smooth quadratic interpolation of the energy as a function of the number of electrons, because the only contribution at the local level in ΔfT(r) comes from Δf(r). An important consequence of this result is that the regioselectivity information enclosed in the dual descriptor is never lost at any temperature different from zero.

(1) Parr, R. G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford UP: New York, NY, USA, 1989.

(2) Chermette, H. J. Comp. Chem. 1999, 20, 129.doi: 10.1002/(SICI)1096-987X(19990115)20:1＜129::AID-JCC13＞3.0.CO;2-A

(3) Geerlings, P.; De Proft, F.; Langenaeker, W. Chem. Rev. 2003, 103,1793. doi: 10.1021/cr990029p

(4) Gázquez, J. L. J. Mex. Chem. Soc. 2008, 52, 3.

(5) Chattaraj, P. K. Chemical Reactivity Theory: A Density Functional View; CRC Press: Boca Raton, FL, USA, 2009.

(6) Liu, S. B. Acta Phys. -Chim. Sin. 2009, 25, 590.doi: 10.3866/PKU.WHXB20090332

(7) Johnson, P. A.; Bartolotti, L.; Ayers, P. W.; Fievez, T.; Geerlings, P.Charge Density and Chemical Reactions: A Unified View from Conceptual DFT. In Modern Charge-Density Analysis; Gatti, C.,Macchi, P., Eds.; Springer: Dordrecht, The Netherlands, 2012;pp. 715–764.

(8) Parr, R. G.; Donnelly, R. A.; Levy, M.; Palke, W. E. J. Chem. Phys.1978, 68, 3801. doi: 10.1063/1.436185

(9) Mulliken, R. S. J. Chem. Phys. 1934, 2, 782. doi: 10.1063/1.1749394(10) Iczkowski, R.; Margrave, J. L. J. Am. Chem. Soc. 1961, 83, 3547.doi: 10.1021/ja01478a001

(11) Pearson, R. G. J. Am. Chem. Soc. 1963, 85, 3533.doi: 10.1021/ja00905a001

(12) Pearson, R. G. Science 1966, 151, 172.doi: 10.1126/science.151.3707.172

(13) Parr, R. G.; Pearson, R. G. J. Am. Chem. Soc. 1983, 105, 7512.doi: 10.1021/ja00364a005

(14) Pearson, R. G. J. Chem. Educ. 1987, 64, 561.doi: 10.1021/ed064p561

(15) Pearson, R. G. Inorg. Chim. Acta 1995, 240, 93.doi: 10.1016/0020-1693(95)04648-8

(16) Pearson, R. G., Chemical Hardness: Applications from Molecules to Solids; Wiley-VCH: Oxford, UK, 1997.

(17) Parr, R. G.; Yang, W. T. J. Am. Chem. Soc. 1984, 106, 4049.doi: 10.1021/ja00326a036

(18) Yang, W. T.; Parr, R. G.; Pucci, R. J. Chem. Phys. 1984, 81, 2862.doi: 10.1063/1.447964

(19) Ayers, P. W.; Levy, M. Theor. Chem. Acc. 2000, 103, 353.doi: 10.1007/s002149900093

(20) Morell, C.; Grand, A.; Toro-Labbe, A. J. Phys. Chem. A 2005, 109,205. doi: 10.1021/jp046577a

(21) Morell, C.; Grand, A.; Toro-Labbe, A. Chem. Phys. Lett. 2006, 425,342. doi: 10.1016/j.cplett.2006.05.003

(22) Cardenas, C.; Echegaray, E.; Chakraborty, D.; Anderson, J. S. M.;Ayers, P. W. J. Chem. Phys. 2009, 130, 244105.doi: 10.1063/1.3151599

(23) De Proft, F.; Ayers, P. W.; Fias, S.; Geerlings, P. J. Chem. Phys.2006, 125, 214101. doi: 10.1063/1.2387953

(24) Ayers, P. W.; Morell, C.; De Proft, F.; Geerlings, P. Chem. Eur.J. 2007, 13, 8240. doi: 10.1002/chem.200700365

(25) De Proft, F.; Chattaraj, P. K.; Ayers, P. W.; Torrent-Sucarrat, M.;Elango, M.; Subramanian, V.; Giri, S.; Geerlings, P. J. Chem. Theory Comput. 2008, 4, 595. doi: 10.1021/ct700289p

(26) Morell, C.; Ayers, P. W.; Grand, A.; Gutierrez-Oliva, S.; Toro-Labbe,A. Phys. Chem. Chem. Phys. 2008, 10, 7239. doi: 10.1039/b810343g

(27) Chamorro, E.; Pérez, P.; Duque, M.; De Proft, F.; Geerlings, P.J. Chem. Phys. 2008, 129, 064117. doi: 10.1063/1.2965594

(28) Cárdenas, C.; Rabi, N.; Ayers, P. W.; Morell, C.; Jaramillo, P.;Fuentealba, P. J. Phys. Chem. A 2009, 113, 8660.doi: 10.1021/jp902792n

(29) Araya, J. I. M. Chem. Phys. Lett. 2011, 506, 104.doi: 10.1016/j.cplett.2011.02.051

(30) Morell, C.; Ayers, P. W.; Grand, A.; Chermette, H. Phys. Chem.Chem. Phys. 2011, 13, 9601. doi: 10.1039/c0cp02083d

(31) Geerlings, P.; Ayers, P. W.; Toro-Labbe, A.; Chattaraj, P. K.; De Proft, F. Accounts Chem. Res. 2012, 45, 683. doi: 10.1021/ar200192t

(32) Tognetti, V.; Morell, C.; Ayers, P. W.; Joubert, L.; Chermette, H.Phys. Chem. Chem. Phys. 2013, 15, 14465. doi: 10.1039/c3cp51169c

(33) Morell, C.; Gázquez, J. L.; Vela, A.; Guegan, F.; Chermette, H. Phys.Chem. Chem. Phys. 2014, 16, 26832. doi: 10.1039/c4cp03167a

(34) Guegan, F.; Mignon, P.; Tognetti, V.; Joubert, L.; Morell, C. Phys.Chem. Chem. Phys. 2014, 16, 15558. doi: 10.1039/c4cp01613k

(35) Tognetti, V.; Morell, C.; Joubert, L. J. Comp. Chem. 2015, 36, 649.doi: 10.1002/jcc.23840

(36) De Proft, F.; Forquet, V.; Ourri, B.; Chermette, H.; Geerlings, P.;Morell, C. Phys. Chem. Chem. Phys. 2015, 17, 9359.doi: 10.1039/c4cp05454g

(37) Guegan, F.; Tognetti, V.; Joubert, L.; Chermette, H.; Luneau, D.;Morell, C. Phys. Chem. Chem. Phys. 2016, 18, 982.doi: 10.1039/c5cp04982b

(38) Perdew, J. P.; Parr, R. G.; Levy, M.; Balduz, J. L. Phys. Rev. Lett.1982, 49, 1691. doi: 10.1103/PhysRevLett.49.1691

(39) Zhang, Y. K.; Yang, W. T. Theor. Chem. Acc. 2000, 103, 346.doi: 10.1007/s002149900021

(40) Yang, W. T.; Zhang, Y. K.; Ayers, P. W. Phys. Rev. Lett. 2000, 84,5172. doi: 10.1103/PhysRevLett.84.5172

(41) Ayers, P. W. J. Math. Chem. 2008, 43, 285.doi: 10.1007/s10910-006-9195-5

(42) Miranda-Quintana, R. A.; Ayers, P. W. J. Chem. Phys. 2016, 144,244112. doi: 10.1063/1.4953557

(43) Heidar Zadeh, F.; Miranda-Quintana, R. A.; Verstraelen, T.; Bultinck,P.; Ayers, P. W. J. Chem. Theory Comput. 2016, 12, 5777.doi: 10.1021/acs.jctc.6b00494

(44) Ayers, P. W.; Morell, C.; De Proft, F.; Geerlings, P. Chem. Eur. J.2007, 13 8240. doi: 10.1002/chem.200700365

(45) Polanco-Ramírez, C. A.; Franco-Pérez, M.; Carmona-Espíndola, J.;Gázquez, J. L.; Ayers, P. W. Phys. Chem. Chem. Phys. 2017, 19,12355. doi: 10.1039/c7cp00691h

(46) Kaplan, T. A. J. Statist. Phys. 2006, 122, 1237.doi: 10.1007/s10955-005-8067-x

(47) Ayers, P. W. Theor. Chem. Acc. 2007, 118, 371.doi: 10.1007/s00214-007-0277-7

(48) Franco-Pérez, M.; Ayers, P. W.; Gázquez, J. L.; Vela, A. J. Chem.Phys. 2015, 143, 244117. doi: 10.1063/1.4938422

(49) Franco-Pérez, M.; Gázquez, J. L.; Ayers, P. W.; Vela, A. J. Chem.Phys. 2015, 143, 154103. doi: 10.1063/1.4932539

(50) Franco-Pérez, M.; Gázquez, J. L.; Vela, A. J. Chem. Phys. 2015, 143,024112. doi: 10.1063/1.4923260

(51) Malek, A.; Balawender, R. J. Chem. Phys. 2015, 142, 054104.doi: 10.1063/1.4906555

(52) Franco-Pérez, M.; Ayers, P. W.; Gázquez, J. L. Theor. Chem. Acc.2016, 135, 199. doi: 10.1007/s00214-016-1961-2

(53) Miranda-Quintana, R. A.; Ayers, P. W. Phys. Chem. Chem. Phys.2016, 18, 15070. doi: 10.1039/c6cp00939e

(54) Franco-Pérez, M.; Ayers, P. W.; Gázquez, J. L.; Vela, A. Phys.Chem. Chem. Phys. 2017, 19, 13687. doi: 10.1039/c7cp00692f

(55) Franco-Pérez, M.; Ayers, P. W.; Gázquez, J. L.; Vela, A. J. Chem.Phys. 2017, 147, 094105. doi: 10.1063/1.4999761

(56) Franco-Pérez, M.; Gázquez, J. L.; Ayers, P. W.; Vela, A. J. Chem.Phys. 2017, 147, 074113. doi: 10.1063/1.4998701

(57) Franco-Pérez, M.; Heidar-Zadeh, F.; Ayers, P. W.; Gázquez, J. L.;Vela, A. Phys. Chem. Chem. Phys. 2017, 19, 11588.doi: 10.1039/c7cp00224f

(58) Franco-Pérez, M.; Polanco-Ramirez, C. A.; Ayers, P. W.; Gázquez, J.L.; Vela, A. Phys. Chem. Chem. Phys. 2017, 19, 16095.doi: 10.1039/c7cp02613g

(59) Miranda-Quintana, R. A. J. Chem. Phys. 2017, 146, 214113.doi: 10.1063/1.4984611

(60) Miranda-Quintana, R. A.; Chattaraj, P. K.; Ayers, P. W. J. Chem.Phys. 2017, 147, 124103. doi: 10.1063/1.4996443

(61) Miranda-Quintana, R. A.; Kim, T. D.; Cardenas, C.; Ayers, P. W.Theor. Chem. Acc. 2017, 136, 135. doi: 10.1007/s00214-017-2167-y

(62) Mermin, N. D. Phys. Rev. 1965, 137, A1441.

(63) Kohn, W.; Vashishta, P. Theory of the Inhomogeneous Electron Gas;March, N. H., Ed.; Plenum: New York, NY, USA, 1983; p. 124.

(64) Parr, R. G.; Chattaraj, P. K. J. Am. Chem. Soc. 1991, 113, 1854.doi: 10.1021/ja00005a072

(65) Chattaraj, P. K.; Cedillo, A.; Parr, R. G. Chem. Phys. 1996, 204, 429.doi: 10.1016/0301-0104(95)00276-6

(66) Chandler, D. Introduction to Modern Statistical Mechanics; Oxford University Press: New York, NY, USA, 1987; p. 288.

(67) Landau, L. D.; Lifshitz, E. M. Statistical Physics; Pergamon Press:Elmsford, NY, USA, 1959.

(68) Franco-Pérez, M.; Gázquez, J. L.; Ayers, P.; Vela, A. J. Chem.Theory Comput. 2017, doi: 10.1021/acs.jctc.7b00940

(69) Yang, W. T.; Parr, R. G. Proc. Nat. Acad. Sci. 1985, 82, 6723.doi: 10.1073/pnas.82.20.6723

(70) Berkowitz, M.; Parr, R. G. J. Chem. Phys. 1988, 88, 2554.doi: 10.1063/1.454034

(71) Ayers, P. W.; Parr, R. G. J. Am. Chem. Soc. 2001, 123, 2007.doi: 10.1021/ja002966g

(72) Sablon, N.; De Proft, F.; Ayers, P. W.; Geerlings, P. J. Chem. Theory Comput. 2010, 6, 3671. doi: 10.1021/ct1004577

(73) Sablon, N.; De Proft, F.; Geerlings, P. J. Phys. Chem. Lett. 2010, 1,1228. doi: 10.1021/jz1002132

(74) Geerlings, P.; Fias, S.; Boisdenghien, Z.; De Proft, F. Chem. Soc.Rev. 2014, 43, 4989. doi: 10.1039/c3cs60456j