The Infl uence of the Exchange-Correlation Functional on the Non-Interacting Kinetic Energy and Its Implications for Orbital-Free Density Functional Approximations

FINZEL Kati,BULTINCK Patrick

Department of Inorganic and Physical Chemistry,Ghent University,281 Krijgslaan,9000 Ghent,Belgium.

1 Introduction

Functional development for the non-interacting kinetic energy1–4has recently regained in interest,as two major research lines:orbital-free density functional theory and embedding approaches benefi t from an appropriate functional description.The fi rst kinetic energy functional dates back to Thomas and Fermi5,6in 1928,even much earlier than the theoretical foundations of density functional theory(DFT)led by Hohenberg and Kohn in their seminal paper7.However,fi nding appropriate density-based functional approximations for the kinetic energy has been proven to be severely diきcult.Thus,the orbital-based Kohn-Sham method(KS)8became the most popular variant of density functional theory.A big issue in the design of kinetic energy functionals is to avoid the variationally obtained electron density to fall into the structureless bosonic-like solution,a well-known defect that is inherently related to the problem of imposing proper N-representability conditions on the functional9–11.

First work was done using conventional gradient expansion techniques5,6,12–15and extended by generalized gradient approximations motivated by conjoint arguments16–18or the fulfillment of additional constraints19–21. But also information-theory motivated functionals22–24,functionals based on response theory25,26,and expansions in terms of moment densities27were studied.In practice it is very diきcult to fi nd suitable kinetic energy functional approximations,which are able to yield electron densities with proper N-fermionic behavior,like for example the atomic shell structure of the radial electron density28–31.This failure is attributed to an insuきcient incorporation of the Pauliexclusion principle21,32,33in the Pauli kinetic energy and the corresponding Pauli potential34.Both terms were intensively studied in the literature35–43as they represent the only unknown part of the kinetic energy functional and the corresponding potential,respectively.Recently,an ad hoc formalism how to construct approximations for the Pauli potential,which are able to yield properly structured electron densities44–47has been presented.A generalized method how to design functional approximations with specifi ed functional derivatives48hasbeen published consecutively.

This work focuses on another important aspect for the design of kinetic energy density functionals:its implicit orbital-dependence.While the explicit orbital-dependence for the kinetic energy is obvious,namely finding a density-based approximation for the kinetic energy which is known in terms of orbitals,the implicit orbital-dependence of the kinetic energy is more subtle.This additional dependence is due to the fact that only the total Fermi potential49is a pure density functional,whereas its both components:the kinetic and the exchange-correlation part,depend on the chosen system,and are thus,orbital-dependent.Whereas this aspect is well-known for the non-interacting versus the real interacting system50,the same applies to the non-interacting Kohn-Sham system itself,due to the diあerent treatment of the exchange-correlation eあects when using diあerent functionals.In fact,the intense relationship between the kinetic and the exchange energy density is known since long time and has lead to the conjoint hypothesis,which was intensively applied in the development of kinetic energy density functional approximations by employing the same enhancement factor for both terms:the kinetic and the exchange component16–18.Here,however,the implicit orbital-dependence is tested or the exact noninteracting kinetic energy.Therefore,the Section 2 deals with the origin of the implicit orbital-dependence for the exact non-interacting kinetic energy,formally derived within an orbital-free formalism,but the numerical data presented in the Section 3 is taken from a conventional KScalculation.

2 Theory

It is a well-known fact that for density functional approximations the exchange and correlation terms are usually treated together as both parts signifi cantly infl uence one another33,51.The aim of this work is to show that the same applies to the kinetic energy if one aims to target orbital-free density functional calculations.The following section deals with theorbital-freederivation of theabove aspect.In contrast,the numerical investigation is carried out with the help of the KS system in order to exclude errors originating from the kinetic energy functional expression itself.

The Hohenberg-Kohn theorems7provide the theoretical foundation for a direct minimization of the total electronic energy of the system E with respect to its electron density ρ(→r)subject to the constraint that the latter stays appropriately normalized to the number of electrons N(0= µ[∫ρ(→r)d→r −N]):

whereby the introduced Lagrange multiplierµequals the chemical potential51.It is possible to split the total energy of the system into energy terms which are independent of the particles nature,and consequently also apply to boson-type particles EB[ρ],and the remaining energy termswhich account for thefermionic natureof theelectrons EF[ρ]:

with:

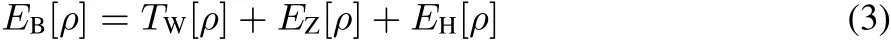
and:

Strictly speaking,theexact correlation functional isnot apurely fermioniceあectasitcounterbalancesthesimplescalingbehavior of the non-interacting kinetic energy resulting from the choice of the KSsystem52.For simplicity,however,thelabel XCiskept as notation.Hereby,the von Weizsäcker kinetic energy TW[ρ]12,the electron-nuclear attraction EZ[ρ](for a system with M nuclei),and the Hartree repulsion energy EH[ρ]belong to the bosonic-like type functionals,and thus,are known as explicit density functionals:

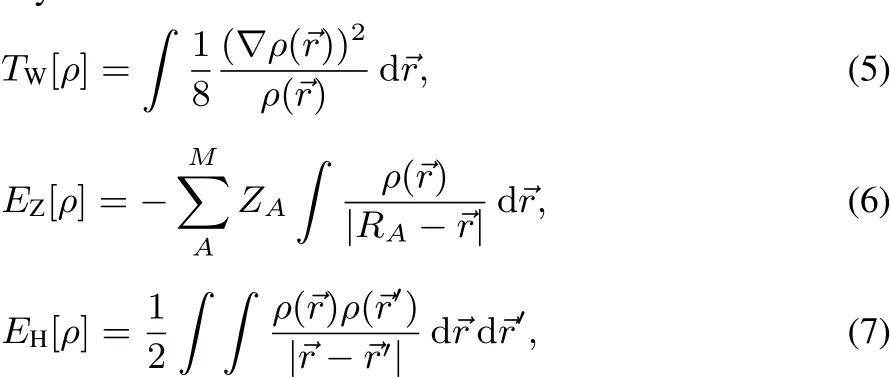
Note that ground-state functionals of the bosonic-type can always be derived by placing the appropriately normalized square root of the electron density into the corresponding orbital-dependent wavefunction expressions.In contrast,the fermionic parts,the Pauli kinetic energy TP[ρ]and the exchange-correlation energy EXC[ρ],are unknown and must be approximated in density functional calculations.By knowledge of the remaining unknown fermionic terms,the electron density could directly be determined from the Euler Eq.(1),whereby each potential vkis the functional derivative of the corresponding density functional vk= δEk/δρ for the energy termsin Eq.(2):

Notice,that the Fermi-potential vF,which isdefi ned asthesum of the kinetic and potential contribution originating from the unknown fermionic energy terms:

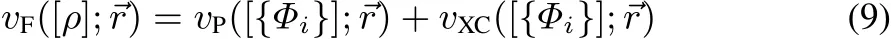
is an explicit density functional and can,at least at the solution point,trivially be obtained from Eq.(8).In practice,the individual parts,however,arenot puredensity functionals,they havean additional orbital dependence.

At the solution point the formal functional derivative of the Pauli kinetic energy,the so-called Pauli potential,can for a single Slater determinant wavefunction(Hartree-Fock(HF)or Kohn-Sham(KS))be expressed in terms of the eigenvalues∈iand eigenfunctions Φi(→r)of the corresponding single particle operator35,53:

with τ(→r)=1/2|∇Φi(→r)|2being the positive kinetic energy density,tW(→r)= 1/8|∇ρ(→r)|2/ρ(→r)being the Weizsäcker kinetic energy density.At the solution point,cf.Eq.(8),the exchange-correlation potential is then numerically equivalent to:

immediately revealing themutual orbital dependenceof thepair vP([{Φi}];→r),vXC([{Φi}];→r).For example,the Pauli potential forthereal interactingsystemdescribed by HFtheory isobtained from the HF eigenfunctions and eigenvalues.In that case,the corresponding exchange-correlation potential(it is a matter of taste whether one would like to call the remaining piece a pure exchange or an exchange-correlation potential,both versions exists in the literature49,54,55)is the Slater potential56.On the other hand it is well-known that the Slater potential is diあerent fromthe KSpotential yielding the HFelectron density54,55,57,in which case theeigenfunctionsof the non-interacting KSsystem are used to evaluate the Paulipotential.

This is caused by the implicit orbital-dependence of the individual pieces vP([{Φi}];→r)and vXC([{Φi}];→r),whereas their sum is orbital-independent,and,thus equal for the HFand the KS system49.Even if the individual components vP([{Φi}]; →r)and vXC([{Φi}];→r)could be modeled correctly by density based approximations,those approximations must be diあerent for the interacting and the non-interacting systems.In the present case,the impact on the potentials is large,as the KS and the Slater potential significantly diあer from one another.The impact on the kinetic energy however,is surprisingly small as shown by the work of Görling and Ernzerhof58.In thisstudy,theimpact on the kinetic energy for the non-interacting KSsystem itself for various treatments of exchange-correlation eあects is investigated.The origin of that dependenceisasin thepreviousexampledueto thesplitting of the total Fermi potential into a kinetic and an exchange-correlation contribution and the mutual infl uence on one another.

In the KSformalism8the non-interacting kinetic energy is given explicitly in termsof orbitals:

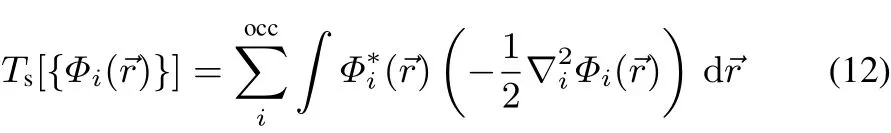
with Φi(→r)obeying the KSeigenvalue equation:

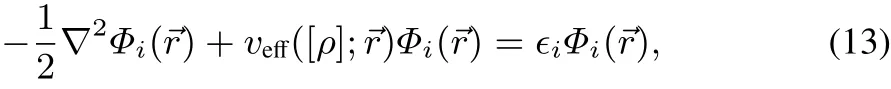
whereby the local multiplicative eあective potential is given by:

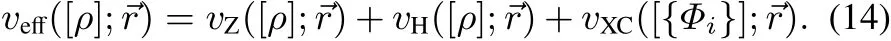
Subtracting veあ([ρ];→r)Φi(→r)from Eq.(13),multiplying with Φ∗i(→r)from the left,and inserting into Eq.(12)yields:

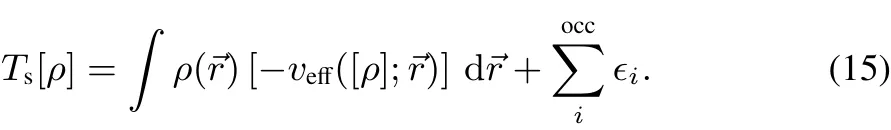
Theaboveexpressionisformally apuredensity functionalforthe non-interactingkineticenergy(asrequired inorbital-freedensity functional theory).However,sinceitwasobtained inthespiritof the KSformalism,it still requiressolving for the N independent particles via Eq.(14)in order to obtain theeigenvalues∈i.From Eqs.(14)and(15)thedirectinfl uenceof vXC([{Φi}];→r)on Ts[ρ]is immediately visible,which is the major aspect of this work.Theorder of magnitude for thisdependence is illustrated in the following section.

3 Results and discussion

KS calculations have been performed with the Gaussian program59for the atoms He,Ne,Ar,Kr,and the CO molecule.The cc-pVQZ basis set60was employed and the following exchange-correlation functionals were tested:LDA8,Xα61,PW9162,63,PBE64,VSXC65,revTPSS66,and B3LYP67.

Fig.1 compiles the diあerences of the non-interacting kinetic energy with respect to the values obtained from LDA ΔTs=TXCs−TLDAsusing various functionals for He,Ne,Ar,and Kr.As can been seen from the dataΔTsincreases with increasing number of electronsin thesystem and is of the order of a few Hartree.Recall that the correlation contribution to the kinetic energy,which is the diあerence between the interacting HF kinetic energy and the non-interacting KS kinetic energy(yielding the HF density)is of the order of a few millihartrees only58.Therefore,the infl uence of the exchange-correlation functional on the non-interacting kinetic energy is of high signifi cance and should be considered when searching for suitabledensity-based functional approximationsfor thekinetic energy.

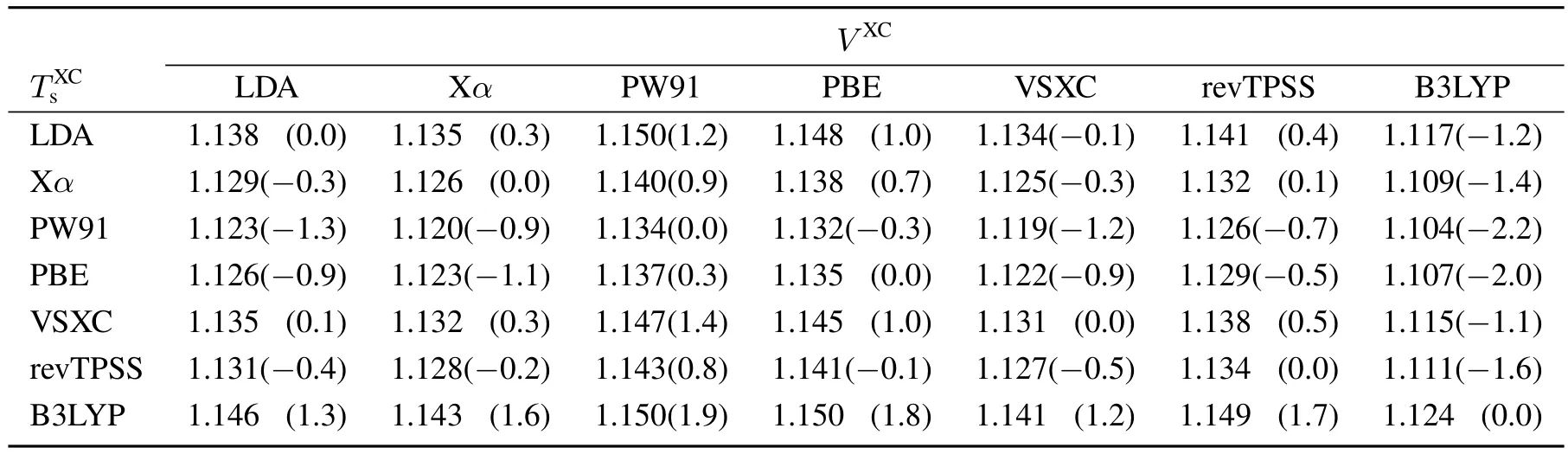
Table1 Bond distancesin for CO using LDA,Xα,PW91,PBE,VSXC,revTPSS,and B3LYP(shown in thediagonal line)aswell astheir combinationsusing T sX C and theremaining total potential energy V XC using theindicated XC functional.

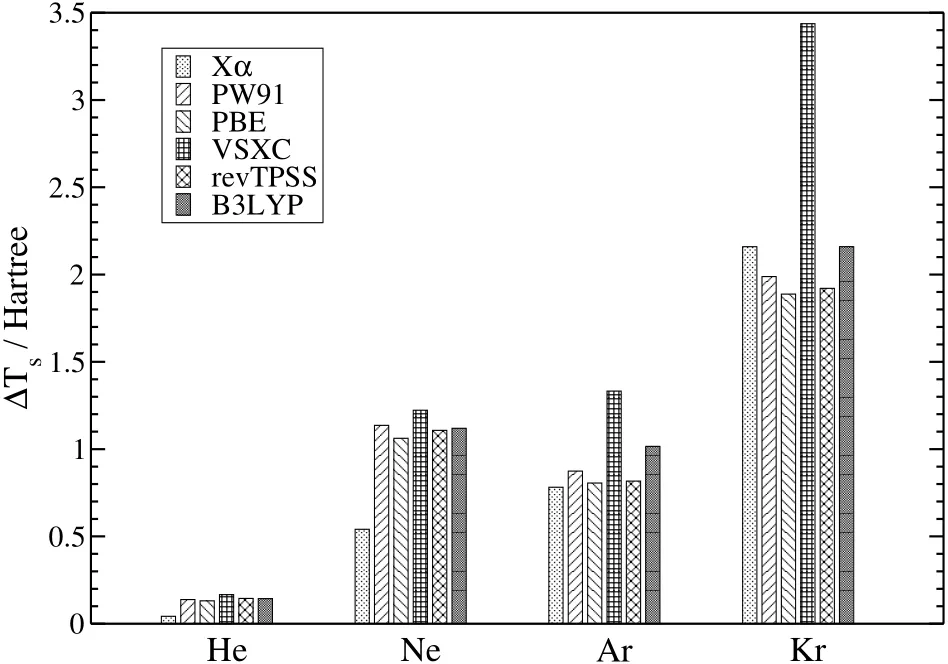
Fig.1 DiあerencesΔT s=T XC s −T LDA s (in Hartree)for XC being Xα,PW91,PBE,VSXC,revTPSS,and B3LYPfor He,Ne,Ar,and Kr,respectively.

From a chemists viewpoint,more crucial than the infl uence onthetotal energy,istheinfl uenceon bond dissociationenergies and bond distances,whichisduetothefactthattheentanglement betweenthekinetic and thepotentialenergy dependsonthebond nuclear coordinates.In case of a dimer,the total kinetic energy as a function of bond distance R:contains a kinetic component TXCs(R)and a potential energy VXC(R)(including the nuclear repulsion).As shown before,both terms depend on the chosen XC functional.If the kinetic energy and the exchange-correlation energy would be suきciently independent of one another(and in the current design of kinetic energy functionals they are treated as if),then the kinetic and potential energy terms as a function of bond distances should roughly be interchangeable for two separate KS calculations obtained with diあerent exchange-correlation functionals.Meaning that the sum of kinetic energy(as a function of bond distance)obtained from an LDA calculation and the remaining potential energy from a PBE calculation should somehow perform as a(possibly weighted)average of the two functionals.To test this assumption,all 49 combinationsusing LDA8,Xα61,PW9162,63,PBE64,VSXC65,revTPSS66,and B3LYP67have been employed in order to obtain the corresponding total energy curves.The bond dissociation curves(total energy of the molecule minus the total energy of thefragments)asafunction of bond distanceare exemplarily shown for the combinations of Xα61,PW9162,63,and PBE64,see Fig.2.The bond distances and dissociation energies for the complete set are compiled in Tables 1 and 2,respectively.As can be seen from Fig.2 the energy minima of the combined functional curves do in general not lie between the minima of the pure(realizable)functional calculations.The same trend is observed for the larger test set,cf.Table 1.Obviously,the mutual infl uence of the kinetic energy and the exchange-correlation functional is large as it shifts the energy minimum beyond the weighted average of the individual energy minima.Therefore,in the design and performance of kinetic energy functionals,theexchange-correlation component isof crucial importanceasthefinal resultssignifi cantly depend upon it.Finally,the performance of a kinetic energy functional must be documented with the corresponding exchangecorrelation component as its stand-alone performance is not reproducibleand thus,of no value.

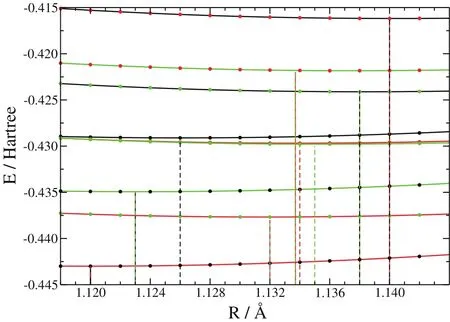
Fig.2 Bond dissociation energy curves versus distancefor the CO moleculecalculated with XC being Xα(shown in black),PW91(shown in red),and PBE(shown in green),and various combinations T sXC (R)and V XC(R).

Notice that,the splitting for the combined data curves with respect to the dissociation energies is even much larger than for the bond distances itself,cf.Table 2.Due to the signifi cant infl uence of the kinetic and exchange-correlation component on each other,the virial ratio is no more fulfi lled for various combinations and consequently,for the corresponding kineticenergy density functional whentrained toreproducetheoriginal KSdata.

Table2 Bond dissociation energies(in Hartrees)for CO using LDA,Xα,PW91,PBE,VSXC,revTPSS,and B3LYP(shown in thediagonal line)aswell as their combinations using T sX C and theremaining total potential energy V using the indicated X C functional.

The above analysis shows that the infl uence of the exchange-correlation functional on the kinetic energy(even if treated correctly within the KSapproach)is beyond the order of chemical accuracy.An uncorrelated treatment of individual kinetic and potential components may signifi cantly alter chemical bonding concepts as it severely infl uences bond distances and dissociation energies.

4 Conclusions

The infl uence of the exchange-correlation potential on the non-interacting kinetic energy is of the order of a few Hartree for total energies.Compared to other eあects,like for example the kinetic correlation contribution,the direct infl uence of the functional choice has a rather large infl uence.Moreover,the mutual dependence of the kinetic and the exchange-correlation functional signifi cantly infl uences bond distances(beyond weighted averages)and the virial ratio.Therefore,the chosen exchange-correlation functional type must be considered in the design of orbital-free density based approximations for the kinetic energy in order to assure the reproducibility of the performance.

Acknowledgement:K.F.wishes to thank Miroslav Kohout for fruitful discussions and substantial encouragement over years.Sofi e Van Damme is gratefully acknowledged for carefully reading the manuscript and valuable criticisms.

(1)Ho,G.S.;Lignères,V.L.;Carter,E.A.Comput.Phys.Comm.2008,179,839.doi:10.1016/j.cpc.2008.07.002

(2)Karasiev,V.;Sjostrom,T.;Trickey,S.B.Computer Phys.Commun.2014,185,3240.doi:10.1016/j.cpc.2014.08.023

(3)Lehtomäki,J.;Makkonen,I.;Caro,M.A.;Harju,A.;Lopez-Acevedo,O.J.Chem.Phys.2014,141,234102.doi:10.1063/1.4903450

(4)Ghosh,S.;Suryanarayana,P.J.Comput.Phys.2016,307,634.doi:10.1016/j.jcp.2015.12.027

(5)Thomas,L.H.Proc.Cambridge Philos.Soc.1927,23,542.doi:10.1017/S0305004100011683

(6)Fermi,E.Zeitschrift für Physik 1928,48,73.doi:10.1007/BF01351576

(7)Hohenberg,P.;Kohn,W.Phys.Rev.B 1964,136,864.doi:10.1103/PhysRev.136.B864

(8)Kohn,W.;Sham,L.J.Phys.Rev.A 1965,140,1133.doi:10.1103/PhysRev.140.A1133

(9)Ayers,P.W.;Liu,S.Phys.Rev.A 2007,75,022514.doi:10.1103/PhysRevA.75.022514

(10)Ludeña,E.V.;Illas,F.;Ramirez-Solis,A.Int.J.Mod.Phys.B 2008,22,4642.doi:10.1142/S0217979208050395

(11)Kryachko,E.S.;Ludeña,E.V.Phys.Rep.2014,544,123.doi:10.1016/j.physrep.2014.06.002

(12)von Weizsäcker,C.F.Z.Phys.1935,96,431.doi:10.1007/BF01337700

(13)Kirzhnits,D.A.Sov.Phys.JETP 1957,5,64.

(14)Hodges,C.H.Can.J.Phys.1973,51,1428.doi:10.1139/p73-189

(15)Murphy,D.R.Phys.Rev.A 1981,24,1682.doi:10.1103/PhysRevA.24.1682

(16)Lee,H.;Lee,C.;Parr,R.G.Phys.Rev.A 1991,44,768.doi:10.1103/PhysRevA.44.768

(17)Fuentealba,P.;Reyes,O.Chem.Phys.Lett.1995,232,31.doi:10.1016/0009-2614(94)01321-L

(18)Tran,F.;Wesolowski,T.A.Int.J.Quantum Chem.2002,89,441.doi:10.1002/qua.10306

(19)Lee,D.;Constantin,L.A.;Perdew,J.P.;Burke,K.J.Chem.Phys.2009,130,034107.doi:10.1063/1.3059783

(20)Karasiev,V.;Chakraborty,D.;Trickey,S.B.Many-Electron Approachesin Physics,Chemistry and Mathematic;Delle Site,L.;Bach,V.Eds.;Springer Verlag:Heidelberg,Germany,2014;pp.113–134.

(21)Karasiev,V.;Trickey,S.B.Adv.Quantum Chem.2015,71,221.doi:10.1016/bs.aiq.2015.02.004

(22)Ghiringhelli,L.M.;Delle Site,L.Phys.Rev.B 2008,77,073104.doi:10.1103/PhysRevB.77.073104

(23)Ghiringhelli,L.M.;Hamilton,I.P.;Delle Site,L.J.Chem.Phys.2010,132,014106.doi:10.1063/1.3280953

(24)Trickey,S.;Karasiev,V.V.;Vela,A.Phys.Rev.B 2011,84,075146.doi:10.1103/PhysRevB.84.075146

(25)Wang,Y.A.;Carter,E.A.Theoretical Methodsin Condensed Phase Chemistry;Schwarz,S.D.Ed.;Kluwer:New York,NY,USA,2000;pp.117–184.

(26)Shin,I.;Carter,E.A.J.Chem.Phys.2014,140,18A531.doi:10.1063/1.4869867

(27)Ayers,P.W.;Lucks,J.B.;Parr,R.G.Acta Chimica et Physica Debrecina 2002,34,223.

(28)Bartell,L.S.;Brockway,L.O.Phys.Rev.1953,90,833.doi:10.1103/PhysRev.90.833

(29)Waber,J.T.;Cromer,D.T.J.Chem.Phys.1965,42,4116.doi:10.1063/1.1695904

(30)Weinstein,H.;Politzer,P.;Srebrenik,S.Theor.Chim.Acta 1975,38,159.doi:10.1007/BF00581473

(31)Schmider,H.;Sagar,R.;Smith,V.H.,Jr.Can.J.Chem.1992,70,506.doi:10.1139/v92-072

(32)Yang,W.Phys.Rev.A 1986,34,4575.doi:10.1103/PhysRevA.34.4575

(33)Dreizler,R.M.;Gross,E.K.U.Density Functional Theory;Springer Verlang:Berlin Heidelberg,Germany,1990.

(34)March,N.H.Phys.Lett.A 1986,113,476.doi:10.1016/0375-9601(86)90123-4

(35)Levy,M.;Ou-Yang,H.Phys.Rev.A 1988,38,625.doi:10.1103/PhysRevA.38.625

(36)Nagy,A.Acta Phys.Hung.1991,70,321.doi:10.1007/BF03054145(37)Nagy,A.;March,N.H.Int.J.Quantum Chem.1991,39,615.doi:10.1002/qua.560390408

(38)Nagy,A.;March,N.H.Phys.Chem.Liq.1992,25,37.doi:10.1080/00319109208027285

(39)Holas,A.;March,N.H.Int.J.Quantum Chem.1995,56,371.doi:10.1002/qua.560560423

(40)Amovilli,C.;March,N.H.Int.J.Quantum Chem.1998,66,281.doi:10.1002/(SICI)1097-461X(1998)66:4<281::AIDQUA3>3.0.CO;2-R

(41)Nagy,A.Chem.Phys.Lett.2008,460,343.doi:10.1016/j.cplett.2008.05.077

(42)Nagy,A.Int.J.Quantum Chem.2010,110,2117.doi:10.1002/qua.22497

(43)Nagy,A.J.Chem.Phys.2011,135,044106.doi:10.1063/1.3607313

(44)Finzel,K.Int.J.Quantum Chem.2015,115,1629.doi:10.1002/qua.24986

(45)Finzel,K.J.Chem.Phys.2016,144,034108.doi:10.1063/1.4940035

(46)Finzel,K.Theor.Chem.Acc.2016,135,87.doi:10.1007/s00214-016-1850-8

(47)Finzel,K.Int.J.Quantum Chem.2016,116,1261.doi:10.1002/qua.25169

(48)Finzel,K.;Ayers,P.W.Theor.Chem.Acc.2016,135,255.doi:10.1007/s00214-016-2013-7

(49)Finzel,K.;Ayers,P.W.Int.J.Quantum Chem.2017,117,E25364.doi:10.1002/qua.25364

(50)Finzel,K.;Baranov,A.I.Int.J.Quantum Chem.2016,117,40.doi:10.1002/qua.25312

(51)Parr,R.G.;Yang,W.Density-Functional Theory of Atomsand Molecules;Oxford University Press:New York,NY,USA,1989.

(52)Levy,M.;Perdew,J.P.Phys.Rev.A 1985,32,2010.doi:10.1103/PhysRevA.32.2010

(53)Bartolotti,L.J.;Acharya,P.K.J.Chem.Phys.1982,77,4576.doi:10.1063/1.444409

(54)Ryabinkin,I.G.;Kananenka,A.A.;Staroverov,V.N.Phys.Rev.Lett.2013,111,074112.doi:10.1103/PhysRevLett.111.013001

(55)Kohut,S.V.;Ryabinkin,I.G.;Staroverov,V.N.J.Chem Phys.2014,140,18A535.doi:10.1063/1.4871500

(56)Slater,J.C.Phys.Rev.1951,81,385.doi:10.1103/PhysRev.81.385

(57)Görling,A.Phys.Rev.A 1992,46,3753.doi:10.1103/PhysRevA.46.3753

(58)Görling,A.;Ernzerhof,M.Phys.Rev.A 1995,51,4501.doi:10.1103/PhysRevA.51.4501

(59)Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;Scuseria,G.E.;Robb,M.A.;Cheeseman,J.R.;Montgomery,J.A.,Jr.;Vreven,T.;Kudin,K.N.;Burant,J.C.;et al.Gaussian 16,Revision A.03;Gaussian,Inc.:Wallingford,CT,USA,2016.

(60)Woon,D.E.;Dunning,T.H.J.J.Chem.Phys.1993,98,1358.doi:10.1063/1.464303

(61)Slater,J.C.Phys.Rev.1969,179,28.doi:10.1103/PhysRev.179.28

(62)Perdew,J.P.;Chevary,J.A.;Vosko,S.H.;Jackson,K.A.;Pederson,M.R.;Singh,D.J.;Fiolhais,C.Phys.Rev.B 1992,46,6671.doi:10.1103/PhysRevB.46.6671

(63)Perdew,J.P.;Burke,K.;Wang,Y.Phys.Rev.B 1996,54,16533.doi:10.1103/PhysRevB.54.16533

(64)Perdew,J.P.;Burke,K.;Ernzerhof,M.Phys.Rev.Lett.1996,77,3865.doi:10.1103/PhysRevLett.77.3865

(65)Van Voorhis,T.;Scuseria,G.E.J.Chem.Phys.1998,109,400.doi:10.1063/1.476577

(66)Perdew,J.P.;Ruzsinszky,A.;Gábor,I.;Constantin,A.L.;Sun,J.Phys.Rev.Lett.2009,103,026403.doi:10.1103/PhysRevLett.103.026403

(67)Becke,A.D.J.Chem.Phys.1993,98,5648.doi:10.1063/1.464913