Perspective:Chemical Information Encoded in Electron Density

CONTRERAS-GARCÍA Julia ,YANG Weitao UPMCUniv Paris06,CNRS,UMR 7616,Laboratoirede Chimie Théorique,casecourrier 137,4 place Jussieu,F-75005,Paris,France.

2 Department of Chemistry,Duke University,Durham,NC 27708,USA.

1 Introduction:DFT and bonding

The last decades have been characterized by a constantly growing interest in the development of exchange-correlation(xc)functionals,Exc=Ex+Ec,within the Kohn-Sham density functional theory(DFT)framework.This has lead to a very large number of functionals being proposed.As a classifi cation scheme,the Jacob ladder was developped,classifying functionals in terms of their explicit ingredients of electron density.The fi rst three rungs are occupied by the so-called semilocal approximations which consist of a single integral for Exc

and where∈xc,the exchange-correlation energy density per electron per unit volume,is a function of the following functions1:

•1st rung:the electron density,ρ,in the local density approximation(LDA),

•2nd rung:ρand itsgradient,∇ρ,inthegeneralized gradient approximation(GGA),and

•3rd rung:ρ,∇ρand the kinetic-energy density and/or the Laplacian,∇2ρ,in the meta-GGA approximation.

Each of these steps of the ladder includes chemical information in terms of 3D functions which is also being used in the analysis of chemical bond,within the Quantum Chemical Topology(QCT)framework2.QCT analyzes the shape of these functions in real space in order to decode the bonding pattern.The most documented example is the electron density.In an approach known as Quantum Theory of Atoms In Molecule(QTAIM),the shape(critical points,zero-fl ux gradient surfaces)of the electron density is used to defi ne chemical concepts such as bonds or atoms3,4.However,many other functions used in QCT derive from other information used in semilocal Density Functinal Approximations(DFAs).The Electron Localization Function5–7and the Localized Orbital Locator8,9are some representative examples.Indeed,ingredients in DFAs are probably the biggest source of chemically meaningful functions used in QCT.However,this connection is not usually acknowledged,not even exploited.DFAs provide functions which are studied in depth within the QCT framework.However,the chemical insight obtained is rarely employed in depth in DFA development.

In this paper,we will focus on analyzing the similarities between both fi elds of knowledge,paying special attention to the use of topological information as a source of insight into DFA behavior.Indeed,this information can be used to better understand the content and the failures of current Exc.With this aim in mind,the paper will be divided into two main sections:(1)the chemical content of the functions used in semilocal DFAs and the progressive inclusion of chemical information along Jacob’s ladder,and(2)the use of chemical content in theunderstanding of DFAs errors,which can beused to understand DFA,or even to help choosing and improving functionals.

2 The chemical content in local functionals

2.1 1st rung:the electron density

The earliest and simplest spin-density functional for the exchange-correlation energy was the local density approximation(LDA)10:

where ∈HEG= ∈HEG[ρ]is the exchange-correlation energy per particleof a Homogeneous Electron Gas(HEG)of densityρ(r).

Just as the electron density is the key property of any electronic system from the energy point of view10,it is also so from the bonding viewpoint.The main chemical properties of the system may be quantitatively calculated fromρ(r).The analysis of the electron density topology provides valuable information on atomic and bonding property,stability and chemical reactivity.

The shape of the electron density can be understood from the analysisof atomic behavior and its superposition11.For an atom,A,thevalueof thedensity at thenucleusposition,rA,can be related to its nuclear charge,ZA:

Fig.1 a)Electron density on a planethat contains the LiH molecule(left).b)Electron density on theplaneperpendicular to the LiH bond that crossesthe BCP(right).

where¯ρ(r)is the spherical average ofρ(r).When going away from the nucleus,an exponential decay is observed,so that at long distances,the asymptotic decay is related with the fi rst ionization potential,I:

Finally,very far away fromthenucleus,theelectrondensity falls to zero:

When a molecule is formed,the general shape of the electron density is dictated by the position of the nuclei(which is described in the external potential).The density shows cusps at thenucleipositions(related to their Z).Fig.1ahighlightsthe position of Liand H atoms in the LiH molecule as cusps of the electron density.

As can be seen from Fig.1a,all the main features of the electron density arealready dictated by the position of atoms Li and H.The relaxation(SCF)cycle leads to a perturbation of this atomic densities.This feature is commonly used in crystallorgraphic studies,where the initial non-relaxed density isused as a first approximation to fi t structure factors.

The existence of bonding interactions can also be derived directly from the electron density.First order saddle points of the electron density(also known as bond critical points-BCPs)appear in between bonded atoms3,4.At the BCPs,the electron density is minimal along the bonding line,and maximal across theperpendicular plane(Fig.1b).

The electron density cusps enable identifying the position,RA,and natureof theatomsinthesystem,ZA.Zerofl uxgradient surfaces can be used to defi ne non-overlapping atomic regions and their properties(e.g.charge,volume).Finally,wecan derive the bonds present in the system from the position of the fi rst order saddle points.

Dr.Contreras-García completed her Ph.D.studies in University of Oviedo with a National grant.She then went to Duke University as a Fulbright student,under the advisory of Prof.Yang.After another year of postdoctoral studieswith Andreas Savin,she obtained her position at CNRSattached to Sorbonne University.She is interested in theories of chemical bonding in Euclidian space and the application to high pressure.In 2013 she received the European Award for young researchers in High Pressure.

2.2 2nd rung:the reduced density gradient

The semilocal information on the electron density was used to introduce the electron density gradient by a second-order gradient expansion (GEA)12and generalized gradient approximation(GGA)13–15,

where F(s)is the enhancement factor,a function of s(r)for a given spin with

Cs=2(3π2)1/3and the 4/3 exponent of the density ensures that s(r)is adimensionless quantity.

The electron density gradient is at the heart of the QTAIM approach,sinceit becomeszero at pointswhereinteractionsare expected.More specifically,as we will see below,properties of s(r)havebeeninvestigated in depthintheprocessof developing increasingly accurate functionals due to its deep relationship with the chemical region of the molecule(shells,bonds)16–21.Indeed,the reduced density gradient can be related to local density inhomogeneities:

•It assumes large values in the exponentially-decaying density tails far from the nuclei,where the density denominator approaches zero more rapidly than the gradient numerator.

•Small values of s(r)occur throughout for the HEG,close to bonding regions,due to the presence of BCPs,and in Lewis pairs,due to its relationship with the One Electron Potential22.

The eあect of these inhomogeneities on the reduced density gradient is especially easy to visualize when s(r)is plotted versusthe density(Fig.2a).Assuming a Slater-type behavior,it is easy to show that graphs of s(r)versusρ(r)assume the form s(r)=aρ(r)−1/3,where a is the Slater exponent.When there is overlap between atomic orbitals,s(r)goes to zero and a spikeappears in the s(ρ)diagram.

Itcanbeshownthattheinformationintroduced by thereduced density gradientisprovidesascaled approximationtothekinetic energy density22:

where twisthevon Weizsäcker kinetic energy density,resulting from assuming a Bosonic behavior(all electrons in the same orbital),and tHEGis the HEGvalue(the Thomas-Fermikinetic energy density):

Fig.2 (a)s(ρ)for water and water dimer.Peaksfor covalent and non-covalent interactionsarelabelled.(b)Chemical features(bond,lonepairs)of N2 asrevealed by s(r)=0.33.

Examplesareshownin Fig.2.Fig.2ashows s(ρ)forwaterand thewater dimer wherethetheinhomogeneity fromthemonomer to the dimer due to the presence of non-covalent interactions(hydrogen bond)is highlighted at small densities23,24.Fig.2b shows the ability of s to reveal electron pairing in real space in N219,25,26.Nitrogen-nitrogen bond and N lone pairs appear as isosurfaces of s.

In real spaceapproaches,thereduced density gradientismost commonly used under the topological approach for revealing non-covalent interactions due to the diきculty to identify them by other means.For example,thefunctionsin Section 2.3.2 only reveal localized electrons,thus they do not reveal non-covalent features.Furthermore,these interactions are also more diきcult to identify from the geometry alone.Whereascovalent radiiare very well defi ned,non-covalentinteractionscover amuch wider range of radiiand angles.Moreover,in many cases they are not localized,so many atomscontributeto thesameinteraction.The reduced density gradientenablesto castthesesituationsinavery intuitiveway.

Fig.3a,b,highlights the ability of the reduced density gradient to provide intuitive insight into localized vs delocalized interactions non-covalent interactions in benzene crystal.Whereaslocalized CH-Cinteractions appear asa small atom-to-atom surface,delocalized CH-πinteractions highlight the interaction of the hydrogen atom with the whole neighboringπsystem.This T-shape interaction is highlighted in Fig.3b.Localization indexes are not able to reveal these features,only the electron density topology(Section 2.1)is able to reveal non covalent interactions,but always as atom-to-atom(localized)visualizations(Fig.3c).

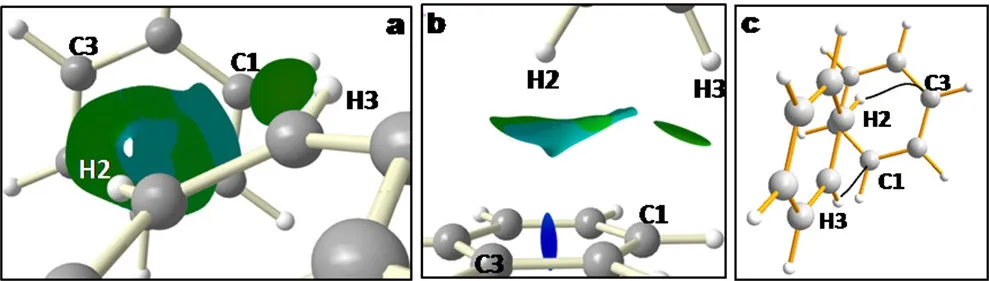
Fig.3 a)s(r)for theintermolecular interactionsin benzenecrystal:localized CH-C interaction(small isosurface)and delocalized CH-π interaction(bigger surface).b)lateral view of the T-shape CH-πinteraction.c)bond paths(QTAIM).

Thus,using all theingredientsof thesecond rung(ρ,∇ρ and s)providesvery richinformationonthechemicalinteractionsof the system,including non-covalent regions.All of them appear aspeaksof thereduced density gradient(s→0).

2.3 3rd rung

Functionals in the third rung of Jacob’s ladder,known as meta-GGAs,include information on the Laplacian and/or kinetic energy density of the calculated Kohn-Sham orbitals.We have seen that the fi rst rung includes information of atoms,the second rung includes information of interactions.What is the information conveyed by the Laplacian and the kinetic energy density?These are functions that highlight electron pairing.We have seen that the reduced density gradient is also able to reveal electron pairing,however,the 3D functions in the 3rd rung make a distinction,they are focused only on electron localization,they do not reveal non-covalent interactions.We will see in the following section how this can be related to the improved performance of meta-GGAs.

2.3.1 The Laplacian

We have seen that within the QTAIM approach,the position of nuclei and bonds are associated with critical points of the density.Within this theory,electron pairing(atomic shells,lone pairs)is recovered from the Laplacian,∇2ρ(r),which is one of the optional pieces of information added to the 3rd rung functionals.

Assuming the electron density can be described byρ(r)=A e−ζr,the Laplacian would be given by:

Themain limiting behaviorsareasfollows:

•It tends to−∞at the nucleus.

•Sincetheelectron density fallsexponentially to zeroatlong distances,so does the Laplacian.

•In between these two asymptotes,the Laplacian in an isolated atom shows maxima and minima with spherical symmetry.These recover the number of shells.This chemical description in atomic shells is also maintained in ionic compounds.

The meaning of the Laplacian can also be understood from its relationship with the electron density gradient through the divergence theorem.According to the divergence theorem27,the sign of the Laplacian of a scalar function indicates whether a net fl ux of the gradient of the scalar is entering(negative sign)or leaving(positive sign)an infinitesimal volume centered on a given point.Hence the sign of the Laplacian of the density informs us on whether the the electron density is concentrating/compressing or diluting/expanding at the point.This yields to the Laplacian as a descriptor of charge depletion(accumulation)for a positive(negative)Laplacian28.Another way to interpret it is from,the local expression of the virial theorem3,29:

where

is the positive defi nite kinetic energy density calculated from the molecular orbitalsφi,and V(r)is the potential energy density.Since t(r)is positive everywhere and V(r)isnegative in most chemical cases regions(e.g.it is asymptotically positive in dianions),the theorem states that the sign of∇2ρ(r)determines which energy contribution,potential or kinetic,is in local excess relative to their average virial ratio of minus two.Most generally,a negative Laplacian reveals that the potential energy is in local excess(shared-electron situation),while a positive Laplacian denotes that the kinetic energy is locally prevailing(closed-shell situation).

Fig.4a highlights the ability of the Laplacian to reveal the shells in MgO:two for Mg2+(K and L)and same for O2−.In covalentcompounds,thevalencebecomesunited(see C2in Fig.4b).This diあerent picture enables to distinguish bonding types in termsof thesign of the Laplacian28.It can beseen thatin the fi rstcase(MgO)thisleadsto∇2ρ＞ 0 in theinteratomic region,whereas∇2ρ ＜ 0 for C2,as expected from their respective bonding type.

2.3.2 Kinetic energy density

Due to the ability of the fi rst order density matrix to reveal non local eあects,kinetic energy densities are a good option to introduceextrabonding information and non-local information.Since the kinetic energy density is not uniquely defi ned,the positive defi nite option,t,is usually used in bonding analyses,as it enables an easier interpretation.

Fig.4 −∇2ρ(r)mapsacrosstheplanethat containsthenuclei a)MgO(Mg on theleft,O on theright).b)C2.

2.3.3 LOL

The Localized Orbital Locator(LOL),v8,was introduced by Schmider and Becke as an intuitive measure of the relative speed of electronsasthekinetic energy density,t,scaled by the HEGvalue:

The scaling enables eliminating theρ5/3dependence of the kinetic energy density which would hide valence characteristics due to the coregreater densities30,31.

Since v(r)is bounded by zero from below,but has no upper boundary,a Lorentzian mapping is usually used,so that the index,LOL′runs from 0 to 1:

Its name is Localized Orbitals Locator because its 3D shape is determined by the ability of a point r to be described by a localized orbital:

•Atthepositionsof thestationary pointsof localized orbitals,v isdriven to small values(LOL′→ 0).

•In regionsdominated by theoverlap of localized orbitals,v attainslargevalues(LOL′→ 1).

This leads to a distribution of maxima and minima that reveals the atomic shell structure8,9.Morevoer,given its connection with localization,it has been shown to be able to reveal multicenter delocalization when averaged over atomic basins32.

Fig.5(bottom)shows the evolution of LOL′along the N2bondingaxis(red line).Itiseasy toseethatthefunctionidentifi es thepositionof thecores(marked withverticallines),thebonding in between them and the lone pairs on each side.

Fig.5 Scaled reduced density gradient(green)and LOL(red)along internuclear(bottom)and resulting ELFcore(blue)(top)along N2 interatomic axis.

2.3.4 ELF

The two previously introduced kinetic energy density measures(LOL and s)constitute the chemical information used to construct another very well known topological index,the Electron Localization Function(ELF)5.Its kernel,χ,according to Savin’s interpretation is given by7:

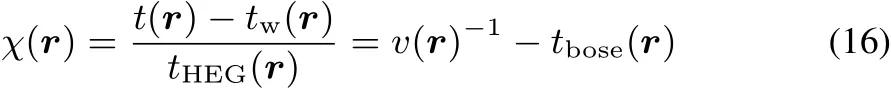
Just like in the case of LOL,the kernel of ELFis re-scaled to provideabounded function:

Remember that tbose=5/6s2.Due to the Pauli principle,electrons(Fermions)are faster on average than if they were Bosons.Hence twis a lower limit for t,and tboseis a lower limit for v−1.This has been highlighted in Fig.5(bottom),where tbose(blue line)has been plotted along with LOL(red line).In other words,ELF has been developed to reveal Pauli behavior and its local eあectson the kinetic energy.

What does this physical meaning lead to?Since Pauli repulsion leads to electron pairing and localization,the following features are obtained:

•The upper limit ELF(r)=1 corresponds to perfect localization.In general,maxima of ELF(r)are identifi ed with regions of high electron localization,such as cores,lonepairs,and covalent bonds.

•When ELFtendsto zero,wearein aboundary region.ELF valueatthesaddlepointshasbeenshown33,34to berelated to the delocalization between fragments via the overlap of the relevant orbitals involved in the interaction.This will beused in Section 3.1.

Fig.6 ELF(r)localization domainsfor:N2(f=0.8).Lonepairs and bond basinsarecoloured in cyan and green,respectively.

Fig.6 highlights ELF’s ability to discern localized electrons in N2.Surfaces of ELF appear at the N cores(not shown),the N≡N bond(in green)and the lone pairs(in cyan).It looks very similar to the LOL(even to the s)picture.One may wonder what istheuseof introducingamorecomplex function to reveal chemical structure.The advantage of ELF is that it is rooted in the Pauli principle.Hence,the topology of ELF renders a quantitative Lewispictureof chemical systems.Asan example,it has been possible to recover the Aufbau principle for shell fi lling from ELFintegration of atomic shellsalong theperiodic table35.This is not possible with LOL nor with s.Its use in meta-GGAs will be highlighted in the next section.

2.4 So what information is encoded in each rung?

The contributions of the diあerent ingredients of semilocal functionals have of course received a lot of attention in the development of new DFAs.It is common practice to analyze the enhancement factor in terms of the reduced density gradient,F(s),as a way to understand its limiting behavior19–21,36.Although less traced,the real space perspective has been also proven to be a rich source of information in understanding the way from one rung to another one.Analyses of F(r)and s(r)19,20,25,37have lead to the understanding of the behavior of the GGA contribution in atoms and molecules,and even to the development of local hybrid functionals.An interesting example of such approach was introduced by Philipsen and Baerends37,who represented LDA and GGA contributions to the cohesive energy on spherical cells along the Cu lattice parameter as the diあerence between the bulk and isolated atoms.This simple plot enables to see the contributions of the GGA term to the cohesion of the solid and to identify that it comes from the bonding region.The analysis above(Section 2.2)enables to understand this observation.Whereas the atomic core enhancement factor is constant from the atom to the bulk,important diあerences appear in s upon cohesion of thesolid.

Maybe more interesting is the analysis of the diあerence between the 2nd rung and the 3rd rung.Since Lewis pairing is already contained to a good approximation in the reduced density gradient,what is the advantage of looking at fermionic kinetic energy densities?

Table 1 provides a summary of kinetic energy density relationships used in the construction of functionals.Bosonic contributions are able to identify all electronic structure features,but they all appear as poles of s,so that GGAs are not able to identify one feature from the others.Kinetic energy measures such as LOL or ELF are able to diあerenciate amongbonding types.

Table1 Valuesof kinetic energy descriptorsin typical bonding types:t b ose(Eq.(8)),v−1(Eq.(14)),z=t W/t(Ref.38),χ(Eq.(16))

Moreover,this approach can even be used to understand failures of a given functional38.Meta-GGAs based on either LOL and ELF(e.g.M06L39and MGGA_MS240)are able to describe equilibrium non-bonding interactions, whereas functionals resorting to z=tw/t,such as revTPSS41,cannot.Looking at Table 1,it is easy to see that while ELF and LOL are able to diあerenciate between covalent,metallic and non-covalent bonding at thebonding critical points,z cannot.

Another example of the usefulness of plots in real space is the analysis of the instability in meta-GGAs.As we have seen,most of the reduced variables used in meta-GGAs show important structuring(critical points),some very steep,even divergent.When combined with small densities,spurious oscillations appear in real space that can be easily understood by plotting thefunctional along interatomic lines42.

All this information can be used to take one further step.It can be used not just to understand failures,but also for improving functionals.Indeed,meta-GGAs were for a long time considered not to introduce great improvements over GGAs.The above analysis has fi nally helped enlarge the GGA vs meta-GGA distance.Favoring ELF information over LOL and z due to its chemical content and stability,Perdew and colaborators have recenlty proposed a new functional which makes meta-GGA systematically superior to GGA,able of describing many diあerent bonding types including insulator to metallic transitions43,44.

3 Identifying(and correcting)DFT errors with chemistry descriptors

Errors in DFT are diきcult to dissect,largely due to the coexistence of various types of errors which aあect the overall performanceof DFT calculations.

One way to try to understand the diあerent factors is to analyze these errors at the most basic level in very simple model atoms.Theseatomic modelsserveto separatethecauses and thus diagnose the failures independently.Following this approach,Yang and coworkers45–48have identifi ed some basic errors which aあect functionals in terms of fractional charges,fractional spins and dispersion interactions.In order to understand what QCT can do for DFA development,we will briefl y describe each of these errors,analyze the 3D functions involved and exploit them to gain insight into the isolated errors.This insight will be further used to provide guidance on thechoiceof functionals,or even,on how to correct them.

3.1 Delocalization error and ELF

3.1.1 The error

Density functional approximations usually underestimatethe barriers of chemical reactions,the band gaps of materials and chargetransfer excitation energies.All theseerrorscan betraced back to acommon root,thedelocalization error46,47.Thiserror can beunderstood fromthestretching of avery simplemolecule,H+2.Atthedissociation limit,thisleadsto two Hatomswith half an electron each.The estimation of the energy of this system from available local functionals is too low(e.g.LDAs,GGAs,and even some hybrid functionals such as B3LYP)15,49.

This can be easily estimated from ensemble densities50:the energyof anatomwithrespecttothenumberof electronsisgiven by straight lines in between integer values.In other words,the energyof a Hatomwithhalf anelectron,should betheaverageof an Hatomwithzeroandoneelectrons.Approximatefunctionals,instead,lead to a convex behavior:they predict incorrect lower energiesfor fractionalelectrons(see Fig.7).Theconsequenceof thisis straight forward:DFAstend to over-delocalize electrons,to artifi cially spread them in themolecule46.

With thissimplemodel it is easy to understand the chemical nature of the above mentioned problems:transition states are systems where bonds are being broken and formed,they are stretched.Hence,theenergy predicted by DFAsismuch too low,and so arethebarriers.Theunderestimation of band gapsisalso a direct consequence of the delocalization error46.It can also be understood within the conceptual DFT framework from the wrong E vs N derivativesof DFAs51.Since Hartree-Fock(HF)leads to the opposite ill-behavior(over-localization,see Fig.7),hybrid functionals may benefi t from error cancellation,leading to good band gap predictions in mid-size gaps.Novel DFAs designed to minimize delocalization error(such as MCY352and CAM-B3LYP53)lead to signifi cant improvement in the accuracy of predicted thermodynamical properties.

3.1.2 Chemical insight-visualizing delocalization error with ELF

To systematically examine the eあect of delocalization error in more complex systems,a series of model chemical systems based on hydrogen chains were designed.Firstly,several 16-hydrogen polymers where put together and lined up head-tohead in an equally displaced manner(Fig.8a)46.1D electron density diあerencemap whereconstructed for 1,2 and 3 of these units upon addition of an extra electron(Fig.9).Diあerences between HFand LDA clearly appear:whereas HFlocalizesthe electron on oneunit,LDA deslocalizesit over several units46.

ELF can be used in order to obtain a closer look at the relationship between the delocalization error and its eあect on the electronic structure.For this purpose,(H2)10chains with changing intermolecular distance d (see Fig.8b)were constructed54.This distance acts as the parameter tunning delocalization error,while other main errors remain negligible or constant.

Fig.7 Variation of theenergy with respect to thenumber of electrons for theexact functional,most DFAs(δN-convex)and HF(δN-concave).

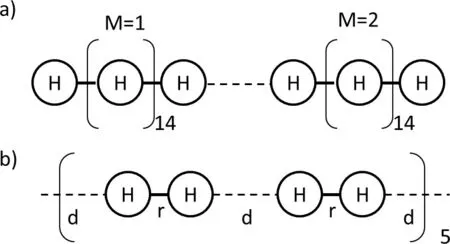
Fig.8 Schematic diagram of a model hydrogen polymers.a)Polymer madeof H16 units.2 units(M=2)areshown.b)Extract of a polymer of H2 units.

Fig.9 Density diあerencemapsfor(H16)M with HF and LDA.

The eあect of delocalization error on the energetics is assessed by analyzing the averaged deviation of calculated adhesive energies(ADE),ΔEad,with respect to highly accurate CCSD(T)data:

Fig.10 (a)Δand(b)Δ||for(H 2)1 0 at variousintermolecular distances d.

where Ead=n E(H2)−E(H2n).

Results for n=10 are shown in Fig.10a.At all values of d,theerrorsfollow theordering:

Thereis only oneexception:at around d=3.0 bohr BLYPand B3LYP’errors become noticeably smaller,wheras HF remain noticeably big.As will be seen below,the system can be described as composed by H2units at this distance,so the lack of correlation in HF becomes more patent(see Section 3.3).Hence,the big admixture with exact exchange at long distances in CAM-B3LYP,worsens the results.

Inordertoassestheincreaseindelocalizationuponincreasing d we have plotted the ELF=0.5 isosurface in Fig.1154.At d=r the chain is encompassed by a continuous isosurface,indicating that it behaves like a macromolecule,with bonding between H2units.As d increases,theten H2unitsbecomemore apparent and at d＞＞ r,each H2unit can be considered as an independent fragment.Each of these fragments are subject to delocalization error.Hence,one would expect the error to increasewith thedistance.However,Fig.10ashowstheopposite trend.It would seem that the error diminishes upon increasing the distance,opposite to what would have been expected from the delocalization point of view.This isbecause theinteraction between two neighboring H2units is weaker at a larger d.If relative errors are analyzed,ΔEDFTad/|ECCSD(T)ad|(Fig.10b),the expected increase in the error appears,indicating that the eあect of delocalization error is indeed more prominent for a morediあuseelectron distribution.

But is this error refl ected in the electronic structure?can we have a glance at the delocalization provided by each functional in this model system?To compare results from each functional,one-dimensional(1D)ELFprofi les along the internuclear axis are plotted in Fig.11.

The polymerized system(d=r)is refl ected in very low diあerence between the ELF value at the maxima and the minima,as expected for a Hnsystem.As the distance in between hydrogen molecules increases(d＞r),fragments are refl ected in a lowering of ELF at the minima.At around d=3.0 bohr,the system can be understood as a chain of weakly interacting H2molecules and thisis refl ected in ELF⋍0 at theminima33.

Moreover,ELF can also be used to understand the delocalization error along the series.HF leads to the lowest values of ELF in the minima,highlighting the description with thisindex of thesystem asmorelocalized H2unitsat each step.As d increases and the system becomes fragment like,ELF from HFcalculations approaches CISD results.As pointed out above,the HFerror at this stage is not related to delocalization but rather to the lack of correlation.Conversely,LDA(and GGA to a lesser extent)leads to values of ELF which are too high at the minima.In this case,the delocalization between units is overestimated.This simple model refl ects that delocalization error is not only refl ected in the energy,but can be easily casted from QCT.

3.2 Fractional spins

3.2.1 The error

One of the most well known failures of DFAs is their inability to describedegenerateor near-degeneratestates(static correlation),such asarisein bond breaking,strongly correlated materials or transition metals.These are manifestations of another error that can be easily identifi ed with a model system,H2,in terms of fractional spins48,55.Opposite to the previous case,when even-electron bonds,as in H2,are stretched,the dissociation limit ispredicted to havetoo high energy.

Following thesameensemble interpretation used in H+2,the dissociation of H2canbedescribed withasingle-referencestate using fractional orbital occupancies.This leads to stretched H2as begin described as two H atoms holding an electron of each spin each45,50,55–58.From this line of thought,it is deduced that the exact energy behaves like a piecewise-fl at-plane as a function of fractional chargesand fractional spins58.In thecase of hydrogen,the exact energy isthen given by:

Fig.11 Evolution of ELF profiles upon stretching of the(H2)10 chain for theindicated d values.Top:isosurfacesfor ELF=0.5(homogeneouselectron gasvalue).Bottom:1D profilesaround thesaddlepoint.

where nαand nβaretheαandβ-spin orbital occupations,and n=nα+nβit the total number of electrons.Thus,a plot of the energy versus nαand nβshould consist of two planes which intersect at nα+nβ=1,leading to a derivative discontinuity.In very rare cases,a second type of fl at plane condition appears, in which the planes intersect at nα− nβ= 059,60.In both cases,violation of the exact discontinuity condition underlies the failure of common functionalsfor strongly-correlated systems58.

Thus,looking at the ability of a functional to provide the correct fl at planes behavior is a measure of their lack of fractional charge and spin errors.Identifi cation of zones of error in functionals and use of chemical information can help improving functionals.Let’s look for example at Becke’s successful non-dynamical correlation (NDC)functional,B0361–63:

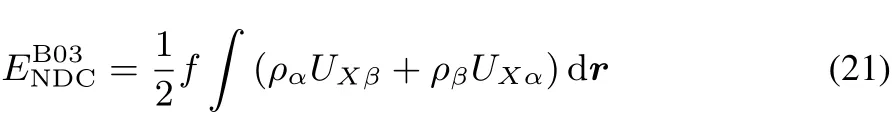
where UXσisthe HFexchangepotentialand f isafractionof the eあectiveopposite-spin exchangehole.Thisapproach recoversa behavior very closeto thefl at plane(Fig.12a).

B03 gives accurate energies in the range 0＜ (nα+nβ)＜1(f=1).The derivative discontinuity is well reproduced.However,a dip appears in the region(nα,nβ)=(0.75,0.75),where the model predicts too much correlation energy.This is due to the fact that Eq.(21)models non-dynamical correlation potential energy,but disregards the kinetic contribution61,62.Thisleadsto an overestimation of the NDCenergy when kinetic contributions are important.We will use chemical information to correct this behavior in the coming subsection.

3.2.2 Chemical insight-correcting Ecwith LOL

In order to correct the ill behavior of B03,it is important to fi rst understand its origin.The model is correct at both extremes[(nα,nβ)=(1,1),and(nα,nβ)=(0.5,0.5)].These two points correspond to the extremes of the binding well: equilibrium and dissociation. But the model overestimates the correlation energy for intermediate coupling strengths[(nα,nβ)=(0.75,0.75)].Asmentioned above,B03 only contains NDC potential energy information.Hence the kinetic energy part is being lost.Thus it can be corrected by using chemical information: the fractional occupation interpretation together with thevirial theorem.

By virtueof the virial theorem,the total NDCenergy is half the NDC potential energy.Hence,the behavior for medium-coupling range can be fi xed by interpolating between strongly-and weakly-interacting regimes.Assuming a linear interpolation,a new version for NDC can be constructed,E:

where g is the coupling factor,defi ned as follows:

Eq.(23)leads to thefollowing values for g:

•g=0 at(nα,nβ)=(1,1)

•g=0.5 at(nα,nβ)=(0.75,0.75)and,

•g=1at(nα,nβ)=(0.5,0.5)and for0＜ (nα+nβ)＜ 1,preserving the exact energy results for this region

Fig.12b shows the results for the correction.The features that were well described are conserved,and the dip at high spin is corrected.Thisisspecially relevantfor stretched bonds(medium rangecorrelation).

But can we go even further using the chemical understanding of the system?It is important to realize that perfectly-localized electron pairs are well described by the monodeterminantal-integer charges scheme.Thus,they are not subject to non-dynamical correlation.This goes back to a well-known concept in chemistry:only valence electrons are aあected by stretching.Coreelectronsbehavior isconstant upon stretching.In other words,the eあective hole normalization in the core is one everywhere whereas in the valence region,the eあective normalization is equal to the fractional occupancy,which can be described by the above corrected model.

Fig.12 Hydrogen-atom electronic energies,asa function of orbital occupation(nα,nβ),for(a)theoriginal B03 density functional and(b)a modifi ed version to fix thefl at planecondition.Lower panelsshow deviationsfrom planarity.

The core-valence separation can be easily done in terms of the Lewis-style descriptors introduced above(e.g.Laplacian,kinetic energy density measures).The Laplacian is known to have failures in identifying the shell structure of heavy elements65.Thus,an indicator based on the kinetic energy densities is more suited.We have used the outer-most LOL maximum to defi ne a distance Rcorewhich divides an atom into core and valence regions.Then the eあective exchange-hole normalizations is defi ned diあerently for these two regions64:

•NeあXσ=1 for the core(r＜R)

•NeあXσ=nσfor the valence(r＞R).

Results for Li and Na atoms are shown in Fig.13.The fl at-plane behavior is recovered for s atoms by this simple chemical input64.This is similar to other chemical informations introduced for treating medium-range separation66,where the local density and gradient information was used to examine chemical bonding.

3.3 Non-covalent interactions

3.3.1 The error

With boosted computational capacities,it has become strikingly clear that the description of dispersion interactions is necessary to capture the chemistry of big structures which are now at reach.Morevoer,it has been shown that dispersion is also crucial in the understanding of smaller systems.Highly branched structures67,and estimations of enantiomeric excess68are some examples.And still,most commonly used functionals are not able to retrieve long-range dispersion interactions due to their inherent non-local nature.

From the 3D point of view,two very diあerent cases appear:intermediateand long distances.Whereassemilocal functionals are not able to correctly describe the latter,some functionals(e.g.PW91)14are able to provide at least qualitatively correct interaction potentials if the fragment electron densities overlap(e.g.at equilibrium).

One interesting equilibrium case which has given rise to much controversy in the literature are 1,3-interactions.It is known that DFAs give systematic errors for very simple reactions.Moreover,just like the H chains analyzed in Section 3.1,these errors increase with system size.

An interesting example of this size dependency is the isodesmic reaction where linear alkanes of growing size are fragmented into ethane molecules69–73:

The atoms involved are main elements from the fi rst row and the number and type of bonds is conserved.Hence,these reactions would be expected to be well described by basically any DFA.This is far from being the case.Results for LDA14and GGAs13,74,75are presented in Fig.14.Whereas LDA performs extremely well,GGAs dramatically fail(errors of up to ca.12 kcal·mol−1(1 cal=4.1868 J)are found for n-octane!).Similar errors have also been reported for isomerization reactions76–80.

Fig.13 Relativeelectronic energies for multielectronic atoms,asa function of orbital occupation(nα,nβ),using our modified non-dynamical correlation functional.(a)Lithium atom(b)Sodium atom.

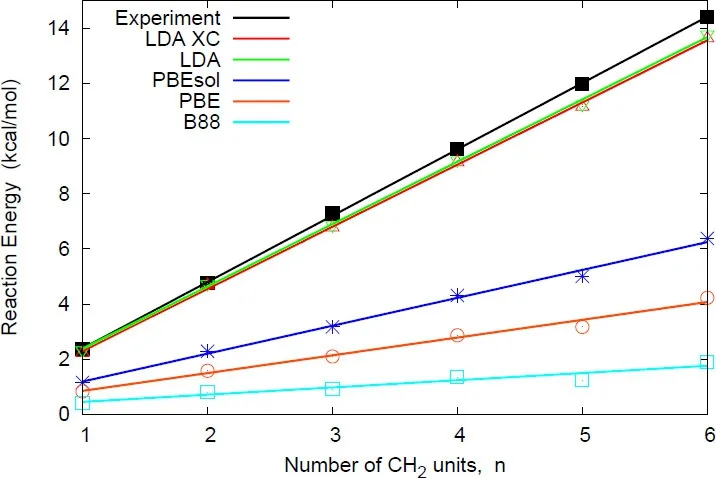
Fig.14 Isodesmic reaction energies(Eq.(24))for then-alkane seriesfrom propanethrough octane.Valuesareexpressed as a function of carbon chain length for the LDA exchange-correlation(XC)functional and exchange-only GGA functionals.

Let’s try to understand the reasons for this apparent failure of the gradient expansion.First of all,if we dissect LDA’s behavior into exchange and correlation,we see that the good performance of LDA is entirely due to the exchange term.LDA(only exchange)and LDA-xc(including correlation)curves nearly overlap(Fig.14).Thus,this is not a correlation eあect and the failure must come from the exchange term.Since GGAs are built from a gradient expansion over LDA,the gradient contribution to the exchange term must be responsible for the incorrect description of isodesmic reactions80,81.Moreover, the error is systematic (reaction energies underestimated)and growswith system size.

Once the part of the functional that is failing is located,we need tounderstand whatitisdoingwrongaboutthechemistry of thesystem.Themaindiあerencewhenlookingattheinteractions in alkanes and ethane,is the absence of 1,3-interactions in the latter.Hence,another isodesmic reactioncanbeconceived where these interactions are still present in order to check whether theerror is coming from a wrong description of these interactions.If we consider the fragmentation of alkanes into propane units:

Table2 Errorsin calculated isodesmic reaction energies(Eq.(24)and Eq.(25))relativeto experiment 83 for linear alkanes up to octane.

the 1,3-interaction is preserved in reactants and products.Table 2 presents the errors per propane observed with diあerent functionals for Eqs.(24)and(25).Now,both GGAs and LDA provide a correct description of Eq.(25).This highlights the fact that the error is indeed localized in the 1,3-interaction,known as protobranching70.

3.3.2 Chemical insight-choosing the correct functional with the reduced density gradient

Since the problem is arising from the inability of the GGA exchangeterm to describenon-covalent1,3-interactions,wecan try to understand the origin of the failure of GGAs in terms of thereduced density gradient,which isthe3D information input inthisterm(see Eq.(6)).Thediあerentperformanceof LDA and GGA should mainly originate from regions with large changes in gradient between ethaneand alarger alkanes,leading to very diあerent contributionsin the GGA term.Fig.15 showsthe s(ρ)plot for ethane and propane.The points that are giving rise to this diあerential behavior are shown in the inset of Fig.15.As expected,they correspond inreal spaceto the1,3-interaction84.

In order to further verify that the 1,3-interaction is at the origin of the GGA missperformance,wehavecompared the DFT integration grid points that were leading to diあerent energetics in between LDA and GGA.These points are shown in blue in Fig.1584:

Fig.15 a)Overlayed s(ρ)plotsfor ethaneand propane.Key grid pointscentered on theleft-most CH3 group,wherethereduced gradient changes by 10%or morebetween ethaneand propane,arehighlighted.Thesepointsare plotted in real spacefor the propanemoleculein the right inset.Theleft inset showsthe non-covalent interaction region,which is an s=1.5 au isosurface containing thosepointsthat fall below thelower edgeof the propane s(ρ)curve.b)s4(ρ)plotsfor ethaneand propane.Electron densities werecalculated with B3LYP/6-31G*15,49,86 and isosurfaces wereobtained using the NCIplot program 87.

•In 3D,they correspond indeed to the protobranching interaction.

•In 2D,they correspond to the dip in the s(ρ)diagram.Since the reduced gradient values are larger for ethane than propane,the exchange energy will be lower.In other words,propaneisdestabilized with respect to ethane.Thisleads to the systematic energy error in protobranching.Moreover,since the error isrelated to agiven local interaction,it will systematically grow with thenumber of interactionsinvolved.

But,once again,can we use our understanding of the problem for obtaining better results?Functionals with a reduced magnitude of the gradient term(such as PBEsol)will lead to smaller errors.However,errors are still too large(see Fig.14).Another option within semilocal functionals,is to reduce the dependency on the reduced density gradient.Higher order terms are less sensitive to gradient changes(Fig.15b).Thus,functionals such as B97D85,which expands PBEto 4th order:

should be expected to provide a better answer.This is indeed the case,yielding errors of 0.23 kcal·mol−1per propane unit.It should be noted that DFAs going beyong the generalized gradient approximation(including dispersion,long-range exact exchange,or MP2 correlation)also restore the good agreement with experimental data69–73.

4 Conclusions

In this Perspective we have reviewed two parallel scientific frameworks which exploit similar information: the development of semilocal functionals and the topological analysis of the electronic structure.These two frameworks are built on 3D scalar functions(the electron density,kinetic energy densities,etc.),which are translated respectively into energies and bonding frameworks.We aimed at merging the information from both approaches and try to understand the information coded in functionals in real space.This information provides insight into what type of bonds we can expect to describe along each set of variables in semilocal functionals.Moreover,it can be used to understand the typical failures of DFT.Here,we have worked through examples the case of fractional electrons,showing that topological indexes are able to reveal delocalization errors.We have also seen how this can be taken one step further,proposing variations of existing functionals to minimize the fractional spin error in alkalis.Finally,the wrong description of non-covalent interactions has been exemplifi ed in 1,3 interactions in alkanes.The unexpected regression along Jacob’s ladder for this case has been explained in terms of the NCI contributions,and has served to guide the choice of approximate functionals.All in all,understanding the chemical bonding,and the behavior of functionals for this specifi c situation should be informative for users in choosing functionals and developers inidentifying the error and improving the performance.

Acknowledgement:We would like to acknowledge Dr.Roberto Boto for Figs.1 and 2 and R.Laplaza for valuable help with the layout.

(1)Perdew,J.P.;Schmidt,K.AIPConference Proceedings2001,577,1.doi:10.106/31.1390175

(2)Popelier,P.L.A.Quantum Chemical Topology in“The Chemical Bond II:100 Years Old and Getting Stronger”;Mingos,D.,Michael,P.,Eds.;Springer:Cham,Switzerland,2016.

(3)Bader,R.F.W.Atomsin Molecules:AQuantum Theory;Oxford Science Publications:Oxford,UK,1990.

(4)Matta,C.F.;Boyd,R.J.An Introduction to the Quantum Theory of Atomsin Molecules;Wiley-VCH Verlag GmbH&Co.:Hoboken,NJ,US,2007.doi:10.1002/9783527610709.ch1

(5)Becke,A.D.;Edgecombe,K.E.J.Chem.Phys.1990,92,5397.doi:10.1063i/1.458517

(6)Silvi,B.;Savin,A.Nature1994,371,683.doi:10.1038/371683a0

(7)Savin,A.;Nesper,R.;Wengert,S.;Fässler,T.F.Angew.Chem.Int.Ed.1997,36,1808.doi:10.1002/anie.199718081

(8)Schmider,H.L.;Becke,A.D.J.Mol.Struct.Theochem.2000,527,51.doi:10.1016/S0166-1280(00)00477-2

(9)Schmider,H.L.;Becke,A.D.J.Chem.Phys.2002,116,3184.doi:10.1063/1.1431271

(10)Hohenberg,P.;Kohn,W.Phys.Rev B 1964,136,864.doi:10.1103/PhysRev.136.B864

(11)Spackman,M.;Maslen,E.J.Phys.Chem.1986,90,2020.doi:10.1021/j100401a010

(12)Gunnarsson,O.;Lunqvist,B.I.Phys.Rev.B 1976,13,4274.doi:10.1103/PhysRevB.13.4274

(13)Becke,A.D.Phys.Rev.A.1988,38,3098.doi:10.1103/PhysRevA.38.3098

(14)Perdew,J.P.;Wang,Y.Phys.Rev.B 1992,45,13244.doi:10.1103/PhysRevB.45.13244

(15)Lee,C.;Yang,W.;Parr,R.G.Phys.Rev.B.1988,37,785.doi:10.1103/PhysRevB.37.785

(16)Sahni,V.;Gruenebaum,J.;Perdew,J.P.Phys.Rev.B 1982,26,4371.doi:10.1103/PhysRevB.26.4371

(17)Pearson,E.W.;Gordon,R.G.J.Chem.Phys.1985,82,881.doi:10.1063/1.448516

(18)Perdew,J.P.;Burke,K.;Ernzerhof,M.Phys.Rev.Lett.1996,77,3865.doi:10.1103/PhysRevLett.78.1396

(19)Zupan,A.;Perdew,J.P.;Burke,K.;Causá,M.Int.J.Quantum Chem.1997,61,835.doi:10.1002/(SICI)1097-461X(1997)61:5＜835::AID-QUA9＞3.0.CO;2-X

(20)Zupan,A.;Burke,K.;Ernzerhof,M.;Perdew,J.P.J.Chem.Phys.1997,106,10184.doi:10.1063/1.474101

(21)Tognetti,V.;Cortona,P.;Adamo,C.J.Chem.Phys.2008,128,034101.doi:10.1063/1.2816137

(22)Boto,R.A.;Contreras-García,J.;Tierny,J.;Piquemal,J.P.Mol.Phys.2015,114,1.doi:10.1080/00268976.2015.1123777

(23)Johnson,E.R.;Keinan,S.;Mori-Sánchez,P.;Contreras-García,J.;Cohen,A.J.;Yang,W.J.Am.Chem.Soc.2010,132,6498.doi:10.1021/ja100936w

(24)Lane,J.R.;Contreras-García,J.;Piquemal,J.P.;Miller,B.J.;Kjaergaard,H.G.J.Chem.Theory Comp.2013,9,3263.doi:10.1021/ct400420r

(25)del Campo,J.M.;Gázquez,J.L.;Alvarez-Mendez,R.J.;Vela,A.Int.J.Quantum Chem.2012,112,3594.doi:10.1002/qua.24241

(26)Boto,R.A.;Piquemal,J.P.;Contreras-García,J.Theor.Chem.Acc.2017,136,139.doi:10.1007/s00214-017-2169-9

(27)Arfken,G.Mathematical Methodsfor Physicists;Academic Press:Orlando,FL,USA,1985.doi:9780123846549

(28)Bader,R.F.W.;Essén,H.J.Chem.Phys.1984,80,1943.doi:10.1063/1.446956

(29)Slater,J.C.J.Chem.Phys.1933,1,687.doi:10.1063/1.1749227

(30)Silvi,B.J.Phys.Chem.A 2003,107,3081.doi:10.1021/jp027284p

(31)Kohout,M.;Pernal,K.;Wagner,F.R.;Grin,Y.Theor.Chem.Acc.2005,113,287.doi:10.1007/s00214-005-0671-y

(32)Becke,A.D.J.Chem.Phys.2000,112,4020.doi:10.1063/1.480951(33)Contreras-García,J.;Recio,J.M.Theor.Chem.Acc.2011,128,411.doi:10.1007/s00214-010-0828-1

(34)Contreras-García,J.;Martin Pendás,A.;Silvi,B.;Recio,J.M.Phys.Chem.B 2009,113,1068.doi:10.1021/jp8069546

(35)Kohout,M.;Savin,A.Int.J.Quantum Chem.1996,60,875.doi:10.1002/(SICI)1097−461X(1996)60:4＜875::AIDQUA10＞3.0.CO;2-4

(36)Sun,J.;Perdew,J.P.;Ruzsinszky,A.Proc.Natl.Acad.Sci.USA 2015,112,685.doi:10.1073/pnas.1423145112

(37)Philipsen,P.H.T.;Baerends,E.J.Phys.Rev.B 1996,54,5326.doi:10.1103/PhysRevB.54.5326

(38)Sun,J.;Xiao,B.;Fang,Y.;Haunschild,R.;Hao,P.;Ruzsinszky,A.;Csonka,G.I.;Scuseria,E.;Perdew,J.P.Phys.Rev.Lett.2013,111,106401.doi:10.1103/PhysRevLett.111.106401

(39)Zhao,Y.;Truhlar,D.G.J.Chem.Phys.2006,125,194101.doi:10.1063/1.2370993

(40)Sun,J.;Haunschild,R.;Xiao,B.;Bulik,I.W.;Scuseria,G.E.;Perdew,J.P.J.Chem.Phys.2013,138,044113.doi:10.1063/1.4789414

(41)Tao,J;Perdew,J.P.;Starorerov,V.N.;Scuseria,G.E.Phys.Rev.Lett.2003,91,146401.doi:10.1103/PhysRevLett.91.146401

(42)Johnson,E.R.;Becke,A.D.;Sherrill,C.D.;DiLabio,G.A.J.Chem.Phys.2009,131,034111.doi:10.1063/1.3177061

(43)Sun,J.;Remsing,R.C.;Zhang,Y.;Sun,Z.;Ruzsinszky,A.;Peng,H.;Yang,Z.;Paul,A.;Waghmare,U.;Wu,X.;et al.Nat.Chem.2016,8,831.doi:10.1038/nchem.2535

(44)Car,R.Nat.Chem.2016,8,820.doi:10.1038/nchem.2605

(45)Cohen,A.J.;Mori-Sánchez,P.;Yang,W.Science 2008,321,792.doi:10.1126/science.1158722

(46)Mori-Sánchez,P.;Cohen,A.J.;Yang,W.Phys.Rev.Lett.2008,100,146401.doi:10.1103/PhysRevLett.100.146401

(47)Cohen,A.J.;Mori-Sánchez,P.;Yang,W.Phys.Rev.B 2008,77,115123.doi:10.1103/PhysRevB.77.115123

(48)Cohen,A.J.;Mori-Sánchez,P.;Yang,W.J.Chem.Phys.2008,129,121104.doi:10.1063/1.2987202

(49)Becke,A.D.J.Chem.Phys.1993,98,5648.doi:10.1063/1.464913

(50)Perdew,J.P.;Parr,R.G.;Levy,M.;Balduz,J.L.Phys.Rev.Lett.1982,49,1691.doi:10.1103/PhysRevLett.49.1691

(51)Geerlings,P.;De Proft,F.;Langenaeker,W.Chem.Rev.2003,103,1793.doi:10.1021/cr990029p

(52)Cohen,A.J.;Mori-Sánchez,P.;Yang,W.J.Chem.Phys.2007,126,191109.doi:10.1063/1.2741248

(53)Yanai,T.;Tew,D.P.;Handy,N.C.Chem.Phys.Lett.2004,393,51.doi:10.1016/j.cplett.2004.06.011

(54)Zheng,X.;Liu,M.;Johnson,E.R.;Contreras-García,J;Yang,W.J.Chem.Phys.2012,137,214106.doi:10.1063/1.4768673

(55)Yang,W.;Zhang,Y.;Ayers,P.W.Phys.Rev.Lett.2000,84,5172.doi:10.1103/physrevlett.84.5172

(56)Perdew,J.P.;Ruzsinszky,A.;Constantin,L.A.;Sun,J.;Csonka,G.I.J.Chem.Theory Comput.2009,5,902.doi:10.1021/ct800531s

(57)Ruzsinszky,A.;Perdew,J.P.;Csonka,G.I.J.Phys.Chem.A 2005,109,11006.doi:10.1021/jp0534479

(58)Mori-Sánchez,P.;Cohen,A.J.;Yang,W.Phys.Rev.Lett.2009,102,066403.doi:10.1103/PhysRevLett.102.066403

(59)Cuevas-Saavedra,R.;Chakraborty,D.;Rabi,S.;Cardenas,C.;Ayers,P.W.J.Chem.Theory Comp.2012,8,4081.doi:10.1021/ct300325t

(60)Yang,D.X.;Patel,A.H.G.;Miranda-Quintana,R.A.;Heidar-Zadeh,F.;González-Espinoza,C.E.;Ayers,P.W.J.Chem.Phys.2016,145,031102.doi:10.1063/1.4958636

(61)Becke,A.D.J.Chem.Phys.2003,119,2972.doi:10.1063/1.1589733

(62)Becke,A.D.J.Chem.Phys.2005,122,064101.doi:10.1063/1.1844493

(63)Dickson,R.M.;Becke,A.D.J.Chem.Phys.2005,123,111101.doi:10.1063/1.2035587

(64)Johnson,E.R.;Contreras-García,J.J.Chem.Phys.Commun.2011,135,081103.doi:10.1063/1.3630117

(65)Shi,Z.;Boyd,R.J.J.Chem.Phys.1988,88,4375.doi:10.1063/1.454711

(66)Krukau,A.V.;Scuseria,G.E.;Perdew,J.P.;Savin,A.J.Chem.Phys.2008,129,124103.doi:10.1063/1.2978377

(67)Johnson,E.R.;Mori-Sánchez,P.;Cohen,A.J.;Yang,W.J.Chem.Phys.2008,129,204112.doi:10.1063/1.3021474

(68)Armstrong,A.;Boto,R.A.;Dingwall,P.;Contreras-García,J.;Harvey,M.J.;Mason,N.;Rzepa,H.R.Chem.Sci.2014,5,2057.doi:10.1039/C3SC53416B

(69)Wodrich,M.D.;Corminboeuf,C.;Schleyer,P.v.R.Org.Lett.2006,8,3631.doi:10.1021/ol061016i

(70)Wodrich,M.D.;Wannere,C.S.;Mo,Y.;Jarowski,P.D.;Houk,K.N.;Schleyer,P.v.R Chem.Eur.J.2007,13,7731.doi:10.1002/chem.200700602

(71)Song,J.W.;Tsuneda,T.;Sato,T.;Hirao,K.Org.Lett.2010,12,1440.doi:10.1021/ol100082z

(72)Grimme,S.Org.Lett.2010,12,4670.doi:10.1021/ol1016417

(73)Steinmann,S.N.;Wodrich,M.D.;Corminboeuf,C.Theor.Chem.Acta 2010,127,429.doi:10.1007/s00214-010-0818-3

(74)Perdew,J.P.;Burke,K.;Ernzerhof,M.Phys.Rev.Lett.1996,77,3865.doi:10.1103/PhysRevLett.77.3865

(75)Perdew,J.P.;Ruzsinszky,A.;Csonka,G.I.;Vydrov,O.A.;Scuseria,G.E.;Constantin,L.A.;Zhou,X.;Burke,K.Phys.Rev.Lett.2008,100,136406.doi:10.1103/PhysRevLett.100.136406

(76)Grimme,S.Angew.Chem.Int.Ed.2006,45,4460.doi:10.1002/anie.200600448

(77)Grimme,S.;Steinmetz,M.;Korth,M.J.Org.Chem.2007,72,2118.doi:10.1021/jo062446p

(78)Karton,A.;Gruzman,D.;Martin,J.M.L.J.Phys.Chem.A 2009,113,8434.doi:10.1021/jp904369h

(79)Shamov,G.A.;Budzelaar,H.M.;Schreckenbach,G.J.Chem.Theory Comput.2010,6,477.doi:10.1021/ct9005135

(80)Csonka,G.I.;Ruzsinszky,A.;Perdew,J.P.;Grimme,S.J.Chem.Theory Comput.2008,4,888.doi:10.1021/ct800003n

(81)Brittain,D.R.B.;Lin,C.Y.;Gilbert,A.T.B.;Izgorodina,E.I.;Gill,P.M.W.;Coote,M.L.Phys.Chem.Chem.Phys.2009,11,1138.doi:10.1039/b818412g

(82)Becke,A.D.;Dickson,R.M.J.Chem.Phys.1990,92,3610.doi:10.1063/1.457869

(83)Curtiss,L.A.;Redfern,P.C.;Raghavachari,K.;Pople,J.A.J.Chem.Phys.2001,114,108.doi:10.1063/1.1321305

(84)Johnson,E.R.;Contreras-García,J.;Yang,W.J.Chem.Theor.Comp.2012,8,2626.doi:10.1021/ct300412g

(85)Grimme,S.J.Comput.Chem.2006,27,1787.doi:10.1002/jcc.20495

(86)Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;Scuseria,G.E.;Robb,M.A.;Cheeseman,J.R.;Scalmani,G.;Barone,V.;Mennucci,B.;Petersson,G.A.et al.Gaussian 09,Revision B.01;Gaussian,Inc.:Wallingford,CT,USA,2010.

(87)Contreras-García,J.;Johnson,E.R.;Keinan,S.;Chaudret,R.;Piquemal,J.P.;Beratan,D.N.;Yang,W.J.Chem.Theory Comput.2011,7,625.doi:10.1021/ct100641a