Aromaticity Study of Benzene-Fused Fulvene Derivatives Using the Information-Theoretic Approach in Density Functional Reactivity Theory

YU Donghai, RONG Chunying,*, LU Tian, DE PROFT Frank, LIU Shubin

1 Key Laboratory of Chemical Biology and Traditional Chinese Medicine Research (Ministry of Education of China), College of Chemistry and Chemical Engineering, Hunan Normal University, Changsha 410081, P. R. China.

2 Beijing Kein Research Center for Natural Sciences, Beijing 100022, P. R. China.

3 Research Group of General Chemistry (ALGC), Vrije Universiteit Brussel (VUB), Pleinlaan 2, 1050 Brussels, Belgium.

4 Research Computing Center, University of North Carolina, Chapel Hill, NC 27599-3420, USA.

1 Introduction

Aromaticity is one of the most widely used chemical concepts1. It refers to the extra stability and subsided reactivity of a planar cyclic structure compared to other conformations of the same molecular formula2–5. It is originated from the additional delocalization of electrons, either π, σ, or δ, leading to the redistribution of the electron density of the entire system6–9.Despite of its general acceptance and widespread use, there are still lots of controversies about aromaticity and its counterpart,antiaromaticity, in the literature9–12. This is mainly caused by the fact that there are many different categories of aromaticity discovered in the literature, such as Hückel, Möbius, excited state, spherical, cubic, octahedral, metallic, chelated, and so on13–27. And at the same time there are dozens of aromaticity indexes proposed, whose acronyms include ASE/ISE(aromatic/isomeric stabilization energy), RE (resonance energy), A i (Julg concept), HOMA (harmonic oscillator model of aromaticity), Jug index, Bird index, PDI (para-related delocalization index), FLU (aromatic fluctuation index), MCI(multicenter indices), Iring(multicenter index), ING(normalized I ring), I NB (normalized MCI), ELFπ (electron localization function), ATI (average two-center indices), PLR (para linear response index), AICD (anisotropy of the induced current density), ρRCS(density of ring critical point), NICS (nucleus independent chemical shifts), etc.1,28–36. These descriptors are only indicative of one or few facets of the complicated nature of aromaticity. No single index is able to account for all kinds of aromaticity mentioned above8,37.

Recently, we tackled this matter from a completely different perspective38. Using the quantities we newly developed within the framework of density functional reactivity theory (DFRT)39,40,with substituted fulvene derivatives as the model system, we compared changing patterns of information-theoretic (IT)quantities such as Shannon entropy, Fisher information,Ghosh-Berkowitz-Parr entropy, information gain, Onicescu information energy, and relative Rényi entropy on the ring carbon atoms of these systems with four representative aromaticity indexes, FLU, HOMA, ASE, and NICS38. Our results unveiled two opposite patterns for cross correlations between IT quantities and aromaticity indexes for different ring structures, and these ring-structure-dependent correlations are in good agreement with Hückel’s 4n + 2 rule of aromaticity and 4n rule of antiaromaticity41,42.

In this work, we continue the study using a new model system. We fuse one or more benzene rings, which are known to be aromatic, with fulvene derivatives. The purpose of the present study is to examine whether or not the changing patterns of cross correlations discovered previously are still in place. We are also interested to see if the aromaticity of fused benzene rings is impacted in any manner by the fulvene derivatives. Results obtained from this study should provide further understanding about the nature and origin of aromaticity and antiaromaticity for the systems studied10,19,43,44.

2 Theoretical framework

The original definition of aromaticity features the extra stability of a planar cyclic structure with a conjugated system of 4n + 2 π electrons41. To quantify aromaticity, a number of descriptors have been proposed using different properties as the consequences of aromaticity. We select four representative descriptors from the viewpoint of the energetics (ASE)2,3,5,electron delocalization (FLU)6,35, geometric (HOMA)33, and magnetic (NICS) criteria45, in this study. ASE (aromatic stabilization energies) is an energetics descriptor defined as the total energy difference of an isodesmic or homodesmotic reaction or isomerization between an aromatic structure and its other structures with the same chemical formula. Take benzene or toluene as an example, the simplest isodesmic,homodesmotic, and isomerization reactions representing ASE are, respectively4,5,46,47,

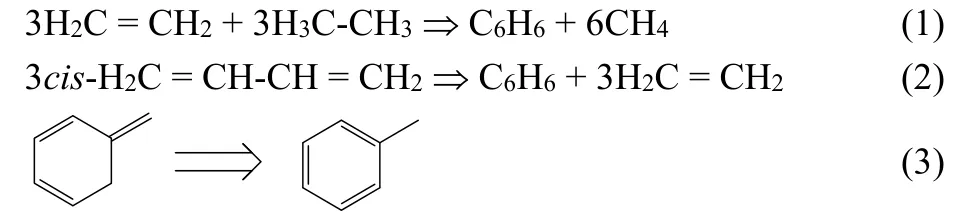
A positive value of ASE denotes that benzene is more stable than its reference, ethylene or 1,3-butadiene, and thus the existence of aromaticity should be in place, whereas a negative ASE value suggests that the system is of antiaromatic nature48.

The HOMA (harmonic oscillator model of aromaticity)index is a geometrical measurement of the equalization of chemical bonds on an aromatic ring. Its definition is the following

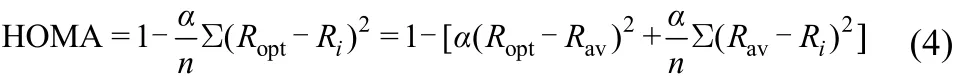
where n is the bond number of the considered ring, R av is the average bond length, Riis the bond length (all in Å, 1 Å = 0.1 nm), of each bond on the ring, and α is the normalization constant (for C―C bonds α = 257.7). A HOMA value of ＜0, = 0, and = 1 represents antiaromatic, nonaromatic, and perfect aromatic systems, respectively33,49.

As an electronic descriptor, the aromatic fluctuation index(FLU) describes the fluctuation of electronic charge between adjacent atoms in a given ring. Its definition is as follows,where Si,j(A) is the overlap of the molecular orbitals i and j within the basin of atom A. The smaller the FLU value, the stronger the aromaticity35.

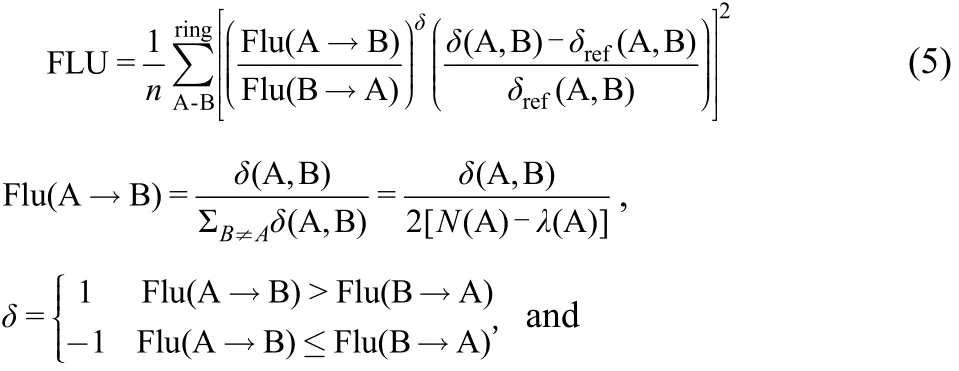
The last one employed in our study is the nucleusindependent chemical shift (NICS) derived from the effect of aromatic ring current. It is found that a diatropic (diamagnetic)ring current is associated with aromaticity, whereas a paratropic(paramagnetic) ring current signals antiaromaticity. This difference in ring currents generates noticeable differences in NMR chemical shifts, and thus can be used to quantify aromaticity and antiaromaticity. In formulation, NICS at the chosen point RNlocated at or on top of a ring can be described as the sum of partial chemical shifts arising from occupied molecular orbitals Ψk0

where the first and second terms on the right-hand side of Eq.(1) are the diamagnetic and paramagnetic contributions,respectively, LN= rN× ▽ refers to the angular momentum operator, rN= r – RN, and r is the electron position. A more negative value of σ is an indication of a stronger aromaticity,whereas a positive σ value suggests that the ring is antiaromatic4,45,50–53.

Our recent tool to deal with aromaticity and antiaromaticity is the information-theoretic approach from DFRT39, where we make use of simple density functionals to appreciate physiochemical properties like aromaticity, steric effect,electrophilicity, nucleophilicity, and stereoselectivity.Quantities considered include Shannon entropy Ss54

Fisher information IF54

Onicescu information energy En of order n55

Ghosh-Berkowitz-Parr (GBP) entropy S GBP39

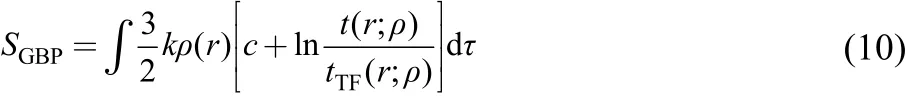
information gain (also called Kullback-Leibler divergence)I G39

and relative Rényi entropy Rrnof order n55,

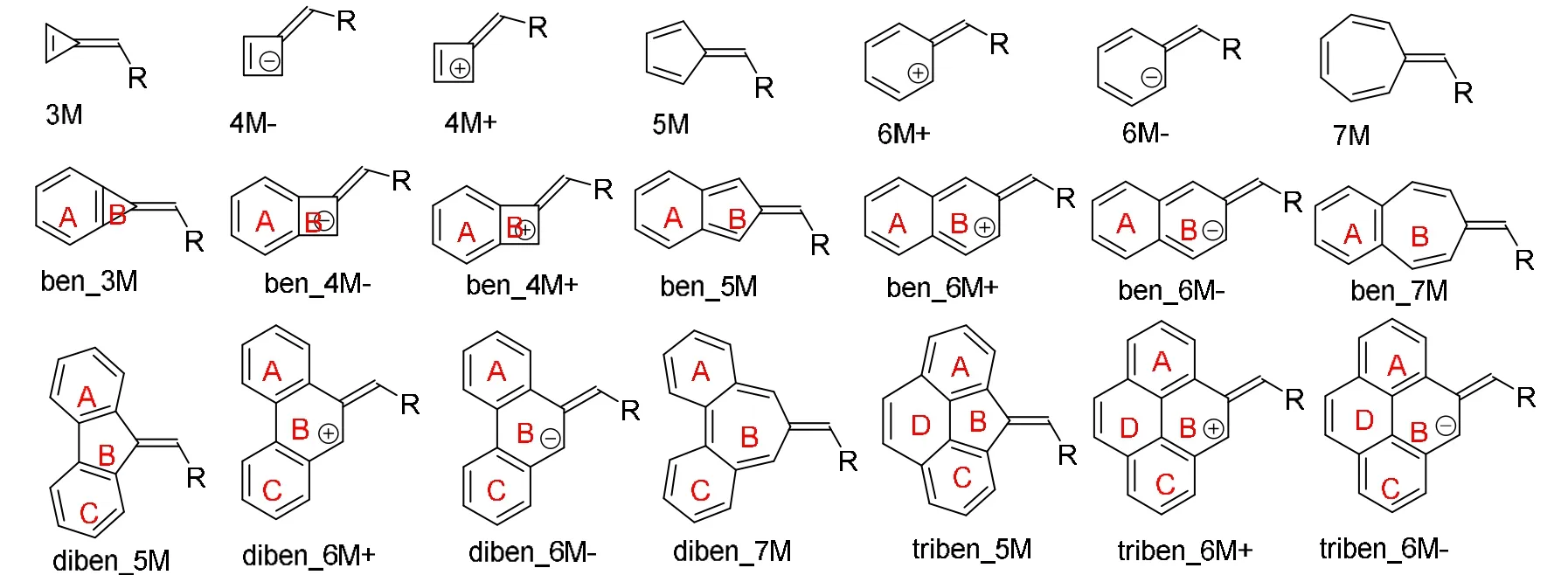
Scheme 1 Substituted fulvene and benzene fused fulvene derivatives examined in this work.

In above formulas, ρ(r) is the electron density, ▽ρ(r) is the density gradient, ρ0(r) is the reference state density satisfying the same normalization condition as ρ(r), t(r; ρ) is the kinetic energy density, t TF(r; ρ)is the Thomas-Fermi kinetic energy density, and c and k are constants. These different theoretical quantities have been previously applied to appreciate numerous molecular processes and physiochemical properties. In this work, we apply them to a new model system and examine their correlations with aromaticity descriptors like NICS, FLU,HOMA and ASE.

3 Computational details

Scheme 1 shows the model systems investigated in this work. Tri (3MR), tetra (4MR+ and 4MR− with one positive and negative charge, respectively), penta (5MR), hexa (6MR+and 6MR−, with one positive and negative charge,respectively), and hepta- (7MR) fulvene derivatives were what we considered before, serving as the reference and thus the starting point of this work. The new systems are fused fulvene derivatives with one, two, and three benzene rings, shown in Scheme 1, denoted by ben_n M, diben_n M, and triben_n M,respectively, with n = 3–7. The rings within the models are marked by A, B, C and D (see Scheme 1), with Ring B standing for the fulvene ring. The substituting groups R was chosen from the following groups, R = H, CH3, CCH, CMe3,CN, CONH2, COCH3, CF3, CH−2, CC−, COO−, F, B(OH)2, OH,OCH3, O−, NH2, NO2, NO, NMe2, NH−, NH3+, NN+, and SiMe356,57, with the criterion that the optimized structure should be planar. Model triben_7M is not planar so it will not be considered here.

All calculations were performed at the DFT B3LYP/6-311G(d,p)58–61level of theory using Gaussian 09 package version E0162with the tight SCF convergence criterion and ultrafine integration grids63. A single-point frequency calculation was followed to ensure that the final structure obtained has no imaginary frequency. The MultiWFN 3.3.9 program developed by one of the present authors was used to calculate all information-theoretic quantities introduced above with the check point file generated from the above Gaussian calculations as the input file64. To obtain the electron density for the isolated state, we employed the spherically-averaged electron density of the neutral atom at the same level of theory. To perform the atomic partition, Becke’s fuzzy atom approach65, Bader’s zero-flux atoms-in-molecules criterion66, and Hirshfeld’s stockholder approach are possible67.As have been demonstrated earlier, these three approaches yield qualitatively similar results55,68,69. In this work, we choose the Hirshfeld’s stockholder approach to partition atoms in molecules to obtain atomic values of above IT quantities on carbons atoms in the aromatic/antiaromatic ring. In this study,we chose NICS(1), which means that the chosen point RN is 1 Å above the center of the aromatic ring30,31. The NICS(1)aromaticity index was calculated using the procedure from the literature7,14,56. The ASE index for fused fulvene derivatives for 3MR-7MR species in Scheme 1 was computed as the total energy difference from the isomerization reaction shown in Scheme 2 with the same level of theory. The aromatic index of FLU and HOMA were calculated using MultiWFN 3.3.9 program at HF/6-311+G(d,f) level of theory61,70. Units for ASE is kJ·mol−1, for NICS is 10−6, and for IT quantities atomic units.

4 Results and discussion

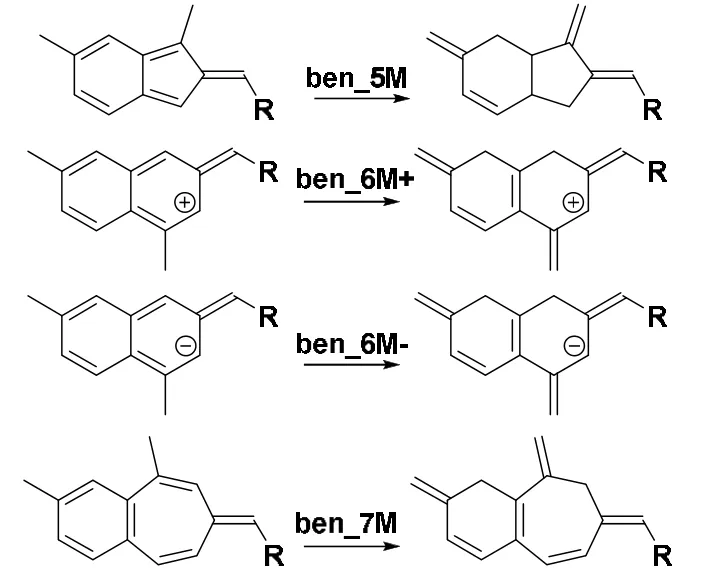
Scheme 2 The isomerization reactions used to calculate the ASE index for singly fused benzofulvenes.

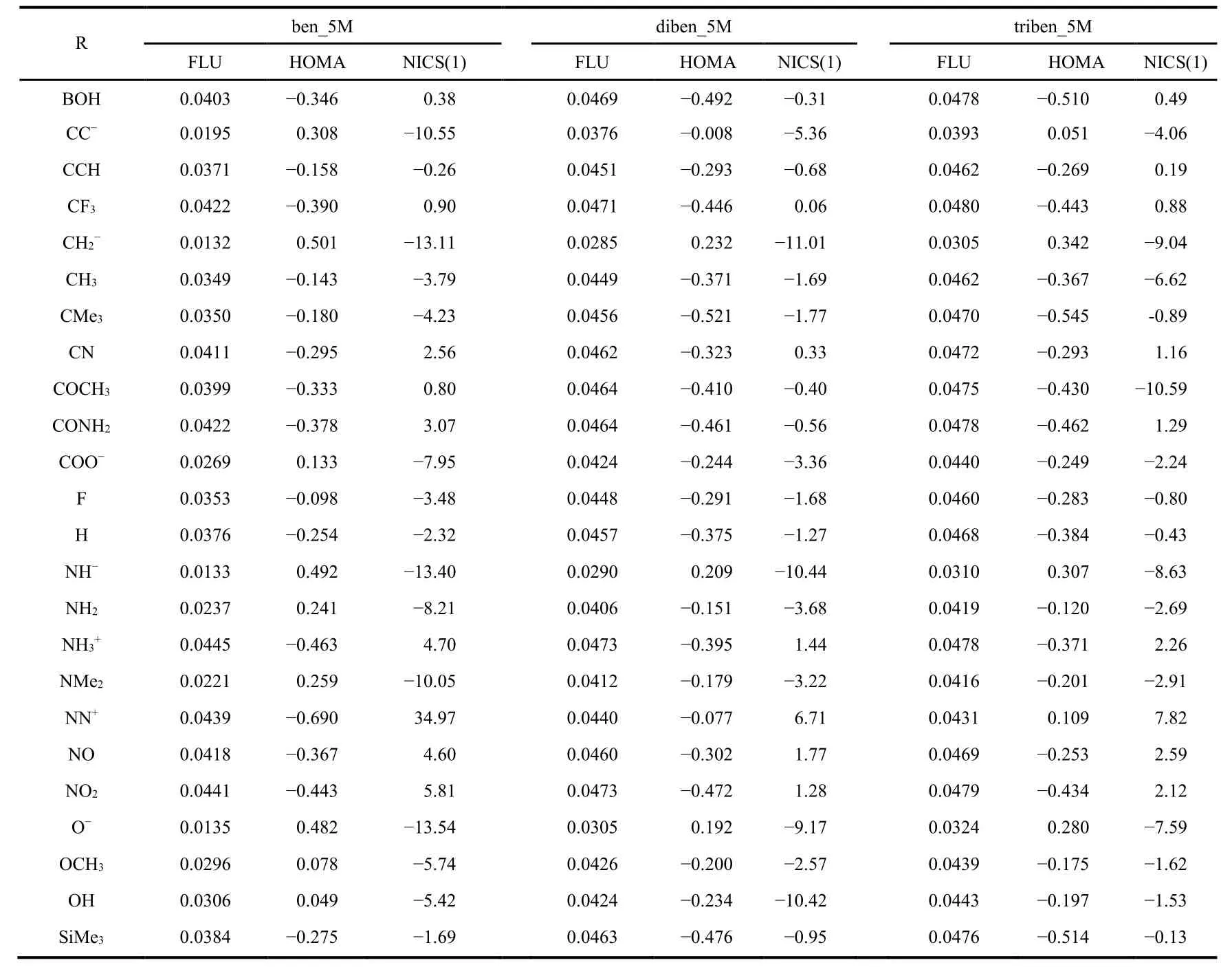
Table 1 Numerical results of FLU, HOMA, and NICS(1) for Ring B of ben_5M,diben_5M, and triben_ben as illustrative examples.

As illustrative examples, Table 1 shows the numerical results of three aromaticity descriptors, FLU, HOMA, and NICS(1),for three benzene fused fulvene derivatives with 25 substituting groups. As can be seen from the table, same as what we have observed in fulvene derivatives; (i) these species could be both aromatic and ant aromatic, according to the definition of each of these aromaticity descriptors; (ii) aromaticity and antiaromaticity depend on the nature of the substituting group;and (iii) different aromaticity descriptors often yield different conclusions on whether a species is aromatic or antiaromatic.Table 2 exhibits the average value of ring carbon atoms of eight information-theoretic quantities, Shannon entropy S S,Fisher information I F, Ghost-Berkowitz-Parr entropy S GBP,information gain I G, Onicescu information energy of orders 2 and 3, E2and E3, and relative Rényi entropy of orders 2 and 3,Rr2and Rr3, for Ring B of the diben_5M system as illustrative examples. Comparing with the data from our previous study for substituted fulvene derivatives, we found that each of these IT quantities is slightly fluctuating around its characteristic(average) value, but, as will be shown below, it is the pattern of their fluctuation that will reflect the nature of aromaticity and antiaromaticity of these systems.

Following our previous work38,69,71–76, Tables 3–5 display the correlation coefficients among the aromaticity and IT quantities studied in this work. Table 3 shows the inter-correlation between each pair of aromaticity descriptors for Ring B of nine benzene fused fulvene systems, from which we can see that the correlation pattern (i.e., positive and negative signs of the correlation coefficient) is always the same. That is, FLU vs NICS(1) is positively correlated (with a positive correlation coefficient), whereas FLU vs HOMA and HOMA vs NICS(1) are negatively correlated. Two points are to be noticed: (i) These correlation patterns are the same as those of fulvene derivatives; and (ii) these patterns are preserved with the changed number of fused benzene rings, with one benzene,to two, and two three fused benzene rings. These results suggest that no matter how many benzene rings are merged with the fulvene ring, the correlation pattern of aromaticity descriptors is always the same. The same tendency is true for IT quantities, as shown in Table 4 for ben_5M, diben_5M, and triben_5M systems as an example, from which the exactly same conclusions can be drawn.

For cross-correlations between aromaticity indices and IT quantities, our previous results have shown that their patterns are dependent of the fulvene ring size. As shown in Table 5,this same conclusion is still valid for benzene fused fulvene derivatives. For example, we find that ben_5M and ben_6M−have opposite changing patterns between aromaticity indices and IT quantities. In addition, this opposite change pattern persists with the increased number of fused benzene rings. That is, from ben_5M, to diben_5M, and to triben_5M, the sign of the correlation coefficient does not change. Again, these results indicate that the correlation pattern of benzene fused fulvene derivatives is dictated the substituted fulvenes.

To visualize the above results, using the correlation between NICS(1) and SGBPas an example, Fig. 1 exhibits the strong linear relationships on the fulvene ring of 0–3 benzene fused systems. The average value of all carbon atoms on the fulvenering was employed in the Figure38,77. A dotted line is used in the Figure to separate aromatic (NICS(1) ＜ 0) and antiaromatic(NICS(1) ＞ 0) regions30,31. As can be seen from the figure,there are two different categories of linear correlations, one with a positive slope and the other with a negative slope, and these patterns do not change with respect to the number of the fused benzenes78,79. Notice that, as indicated earlier, the total number of π electrons in these two categories of correlations are in consensus with Hückel’s 4n + 2 rule of aromaticity and 4n rule of antiaromaticity41.

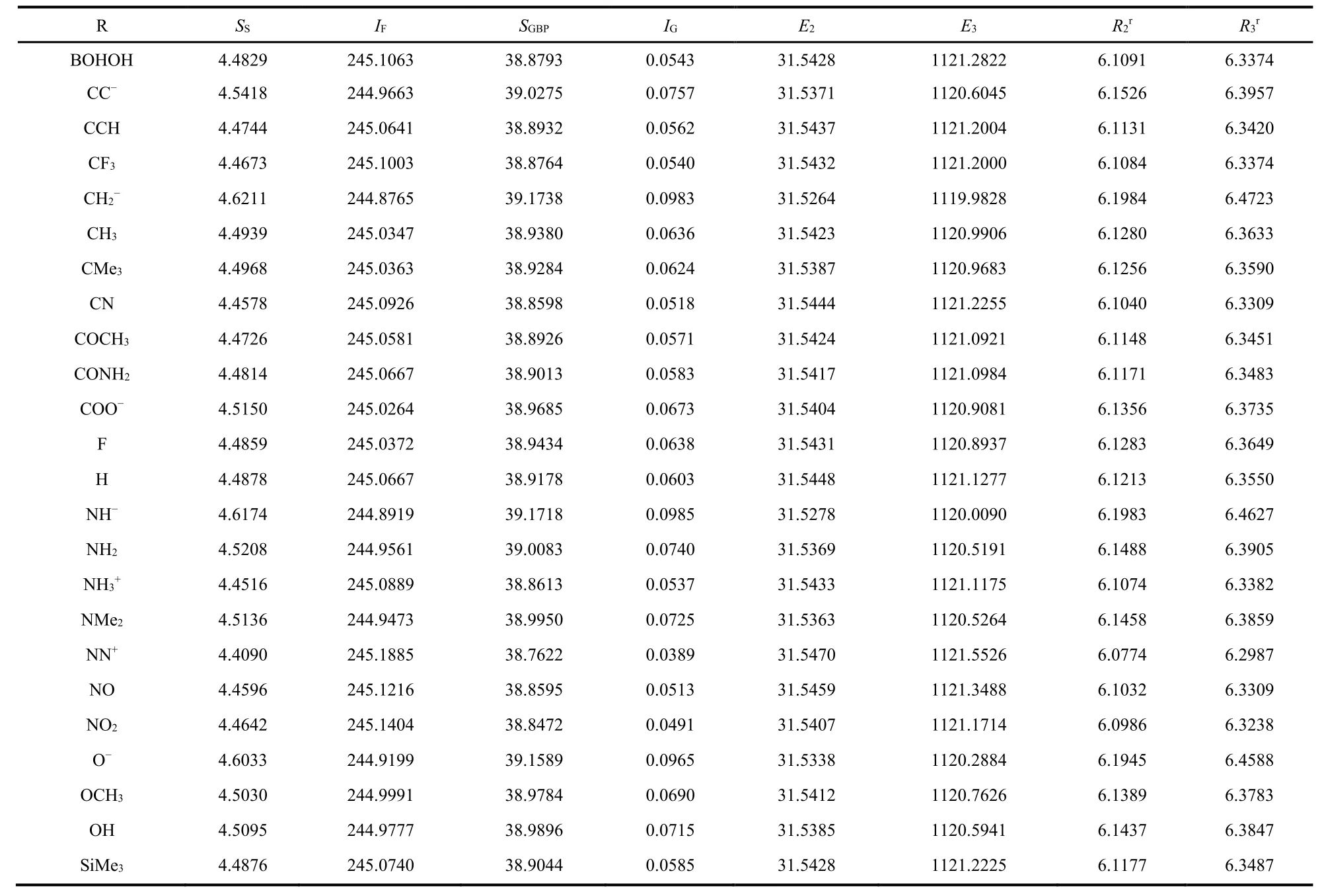
Table 2 Numerical values of information-theoretic quantities for Ring B of diben_5M as illustrative examples.

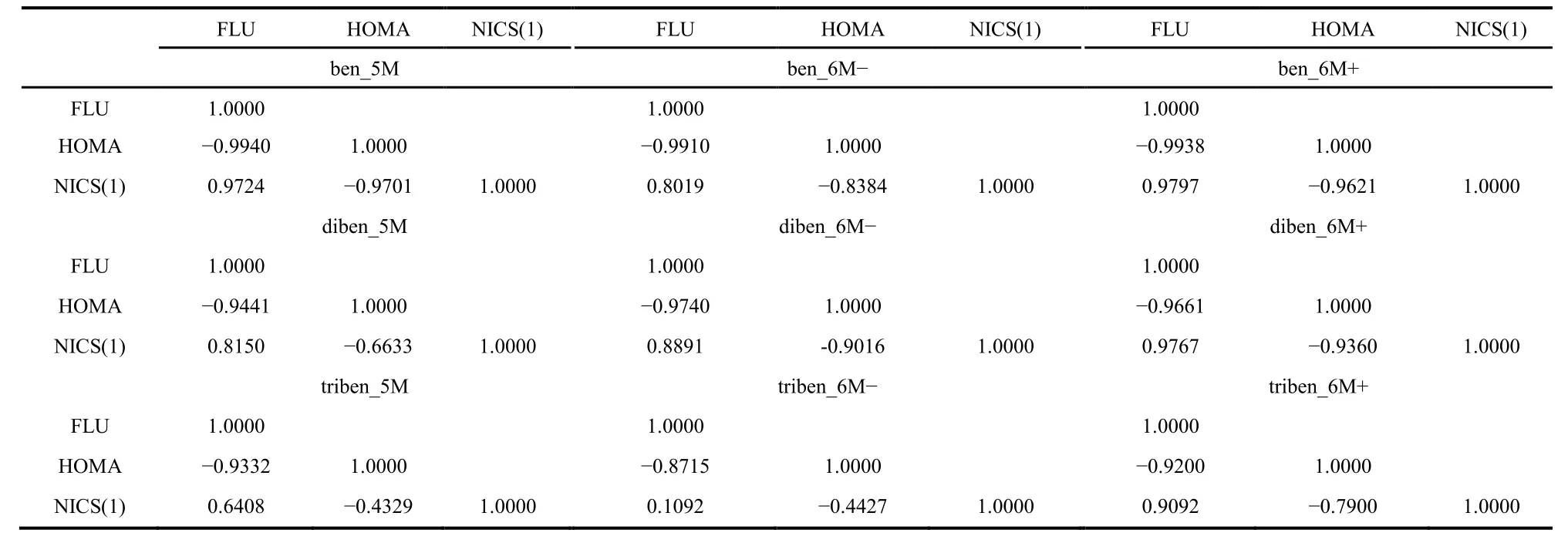
Table 3 The correlation coefficient R between aromaticity indexes FLU, HOMA, and NICS(1) for Ring B of a few benzene fused fulvene systems.

Fig. 2 displays the same correlation patterns between S GBP and NICS(1) of ring A for three benzofulvenes as Fig. 1. It is clear that the correlations are stronger on Ring A than Ring B,even though the qualitative trend is evident. With the difference in that, the correlations in Fig. 2 are for one of the fused benzene rings, not for the fulvene ring. Compared with their counterpart in Fig. 1, it becomes apparent that the pattern of changes with respect to the change of substituting groups between NICS(1) and SGBPis the same, confirming what we concluded earlier that it is the fulvene ring that dictates the changing pattern of the benzofulvene systems38. We know that benzene itself is aromatic, but when fused with fulvene,sometime it becomes antiaromatic, according to the criterion of NICS(1)29–31,45.

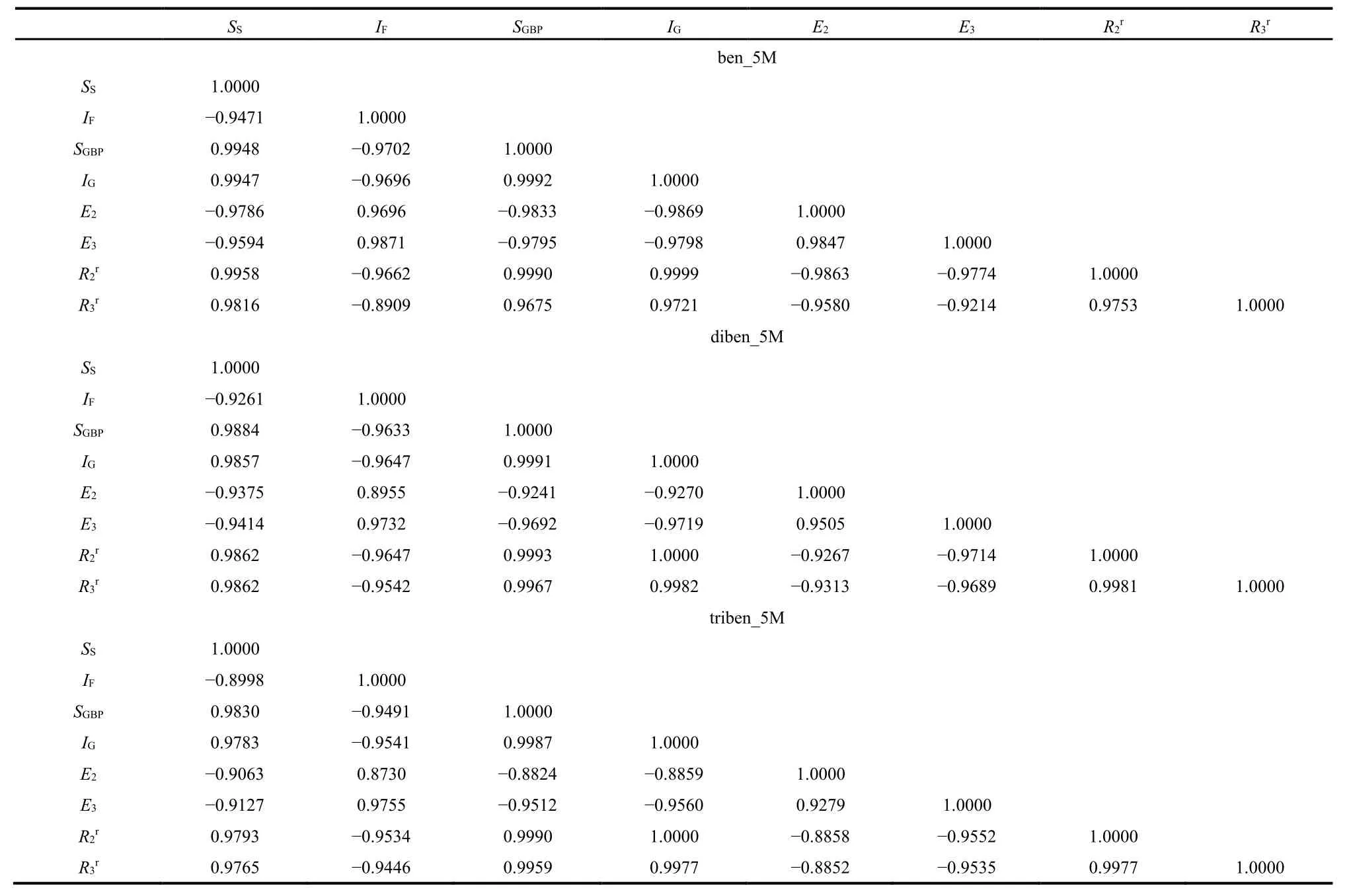
Table 4 The correlation coefficient R between informative quantities for Ring B of a few benzene fused fulvene derivatives.

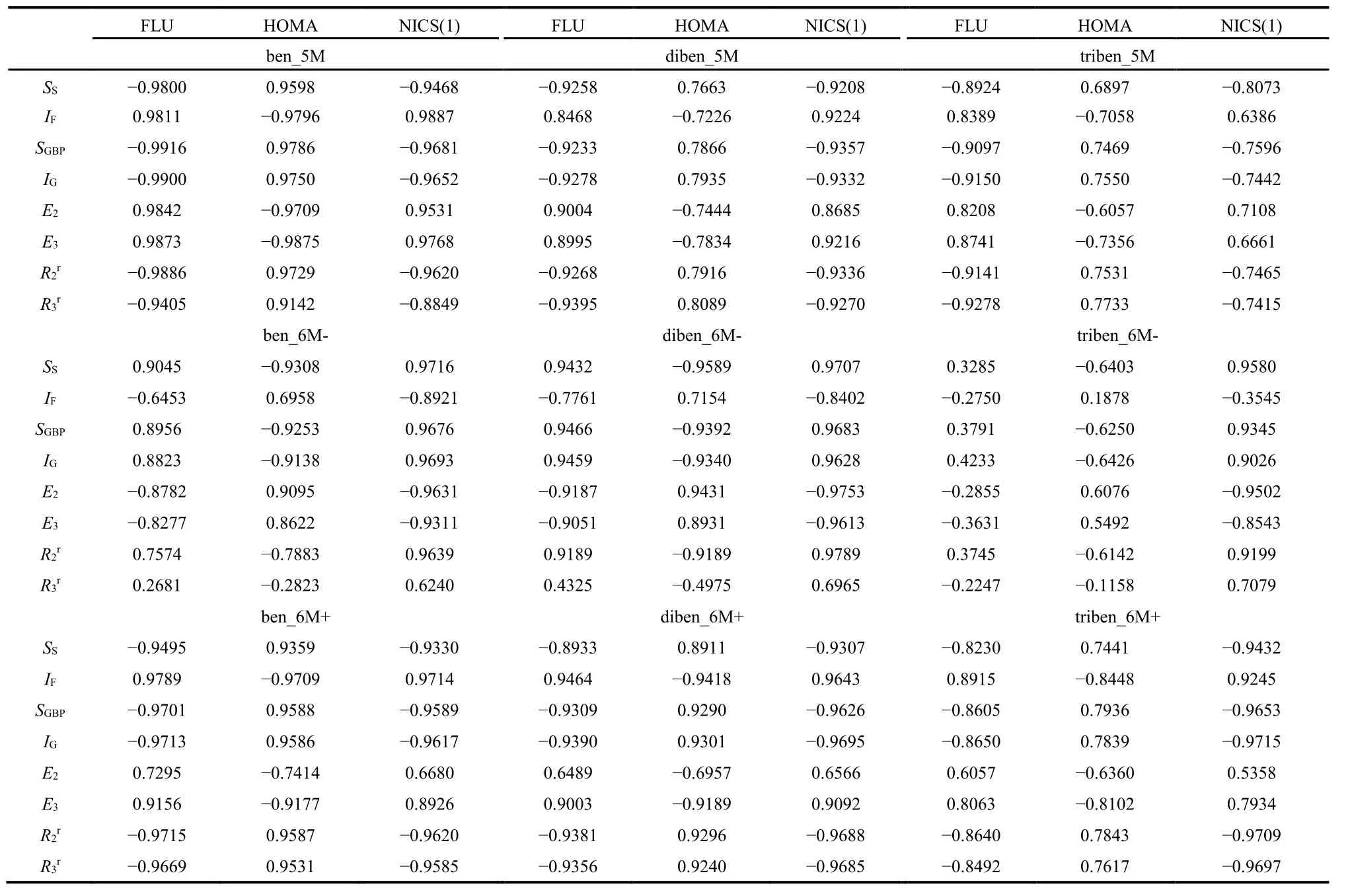
Table 5 The correlation coefficients between aromatic indexes and IT quantities for Ring B of a few benzene fused fulvene derivatives.

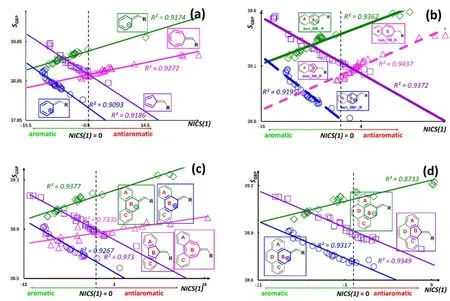
Fig. 1 Strong linear correlations between S GBP and NICS(1) for (a) substituted fulvene derivatives and for Ring B of (b) singly fused benzo fulvenes; (c) doubly fused benzofulvenes; and (d) triply fused benzofulvenes.

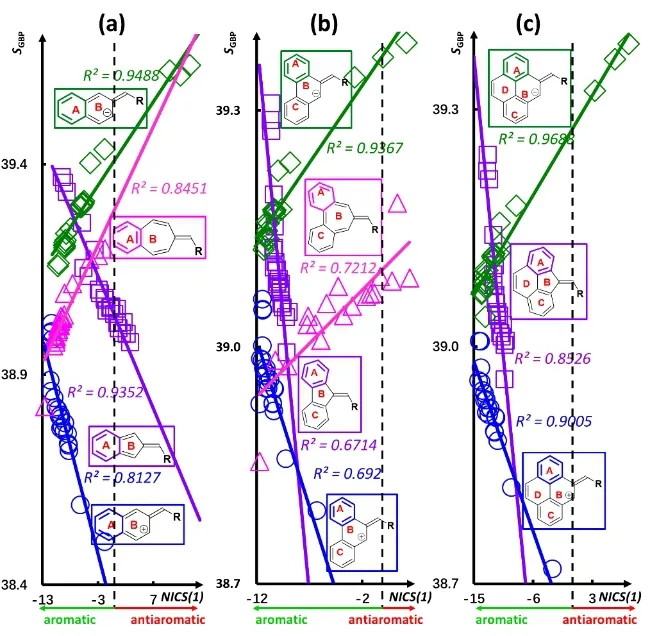
Fig. 2 Strong linear correlations between S GBP and NICS(1) of Ring A for for (a) singly fused benzo fulvenes; (b) doubly fused benzofulvenes;and (c) triply fused benzofulvenes.

To verify our above findings, Fig. 3 shows the ASE correlation results with one of IT quantities, S GBP, for species(a) without and (b) with one benzene fusion. Again, a dotted line is used to separate aromatic and antiaromatic regions.Comparing the plots for the two systems, with and without benzene fusion, it can be readily seen that the changing patterns of ASE with respect to S GBP are the same, each with two positively sloped lines and two negatively sloped lines,respectively. Put together, our results demonstrate that benzene fusion does not change the correlation patterns among aromaticity indices, among IT quantities, as well as cross correlations between these two categories of quantities. The characteristics of these correlations for the benzene fused fulvene derivatives is dictated by the fulvene moiety.

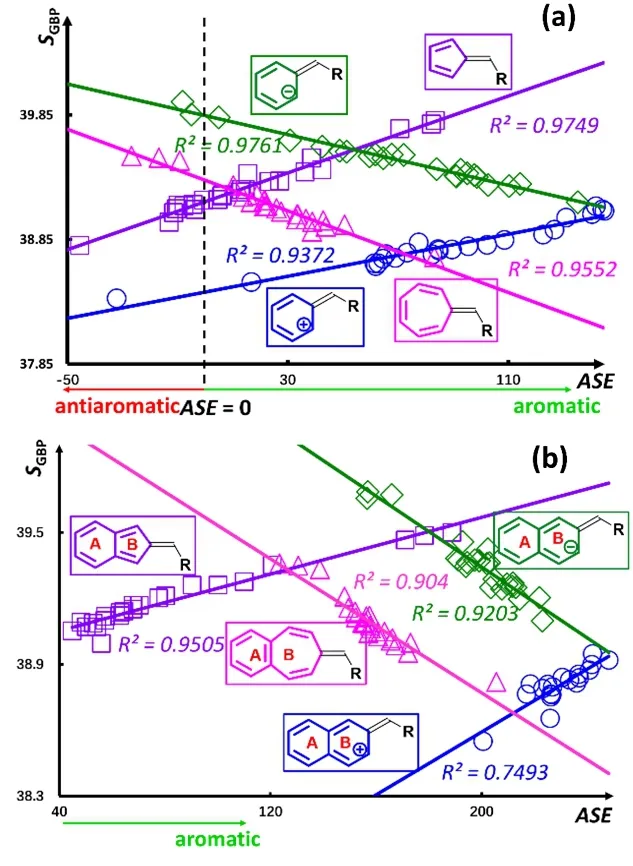
Fig. 3 Strong linear correlations between S GBP and ASE for (a)substituted fulvene derivatives of different ring sizes; and (b) singly fused benzofulvenes.

5 Conclusions

As a continuation of our endeavor to appreciate molecular aromaticity and antiaromaticity using information-theoretic quantities from density functional reactivity theory, in this work, we have systematically examined substituted fulvene derivatives fused with one, two, and three benzene rings. We have considered the correlations, for these systems, among four aromaticity descriptors, ASE, FLU, HOMA, and NICS, and six information-theoretic quantities, Shannon entropy, Fisher information, Ghosh-Berkowitz-Parr entropy, information gain,Onicescu information energy, and relative Renyi entropy, as well as cross correlations between these two categories of properties. Our results show that with and without fused benzene rings, above correlation patterns are the same,suggesting that, even though we know that benzene itself is aromatic, its fusion with the fulvene moiety does not change the characteristics of the aromatic and antiaromatic nature of the fulvene ring. In other words, aromaticity and antiaromaticity of benzene fused fulvene derivatives are solely determined by the fulvene moiety. These results should shed new light on our understanding about the origin and nature of aromaticity and antiaromaticity for this and other systems.

(1) Solà, M. Front. Chem. 2017, 5, 1. doi: 10.3389/fchem.2017.00022

(2) Herndon, W. C.; Mills, N. S. J. Org. Chem. 2005, 70, 8492.doi: 10.1021/jo051289b

(3) Skov, A. B.; Broman, S. L.; Gertsen, A. S.; Elm, J.; Jevric, M.;Cacciarini, M.; Kadziola, A.; Mikkelsen, K. V.; Nielsen, M. B.Chem. -Eur. J. 2016, 22, 14567. doi: 10.1002/chem.201601190

(4) Aihara, J. -I. J. Am. Chem. Soc. 2006, 128, 2873.doi: 10.1021/ja056430c

(5) Cyrański, M. K. Chem. Rev. 2005, 105, 3773.doi: 10.1021/cr0300845

(6) Feixas, F.; Matito, E.; Poater, J.; Solà, M. Chem. Soc. Rev. 2015,44, 6434. doi: 10.1039/C5CS00066A

(7) Sumita, A.; Gasonoo, M.; Boblak, K. J.; Ohwada, T.; Klumpp, D.A. Chem. -Eur. J. 2017, 23, 2566. doi: 10.1002/chem.201606036

(8) Szczepanik, D. W.; Solà, M.; Andrzejak, M.; Pawełek, B.;Dominikowska, J.; Kukułka, M.; Dyduch, K.; Krygowski, T. M.;Szatylowicz, H. J. Comput. Chem. 2017, 38, 1640.doi: 10.1002/jcc.24805

(9) Liu, J. Z.; Ma, J.; Zhang, K.; Ravat, P.; Machata, P.; Avdoshenko,S.; Hennersdorf, F.; Komber, H.; Pisula, W.; Weigand, J. J.; et al. J.Am. Chem. Soc. 2017, 139, 7513. doi: 10.1021/jacs.7b01619

(10) Yoon, Z. S.; Osuka, A.; Kim, D. Nat. Chem. 2009, 1, 113.doi: 10.1038/nchem.172

(11) Frederickson, C. K.; Zakharov, L. N.; Haley, M. M. J. Am. Chem.Soc. 2016, 138, 16827. doi: 10.1021/jacs.6b11397

(12) Boldyrev, A. I.; Popov, I. A.; Starikova, A. A.; Steglenko, D. V.Chem. -Eur. J. 2017. doi: 10.1002/chem.201702035

(13) Marcos, E.; Anglada, J. M.; Torrent-Sucarrat, M. J. Org. Chem.2014, 79, 5036. doi: 10.1021/jo500569p

(14) Stępień, M.; Latos-Grażyński, L.; Sprutta, N.; Chwalisz, P.;Szterenberg, L. Angew. Chem. 2007, 119, 8015.doi: 10.1002/ange.200700555

(15) Szyszko, B.; Sprutta, N.; Chwalisz, P.; Stępień, M.;Latos-Grażyński, L. Chem. -Eur. J. 2014, 20, 1985.doi: 10.1002/chem.201303676

(16) Mobius, K.; Plato, M.; Klihm, G.; Laurich, C.; Savitsky, A.;Lubitz, W.; Szyszko, B.; Stepien, M.; Latos-Grazynski, L. Phys.Chem. Chem. Phys. 2015, 17, 6644. doi: 10.1039/C4CP05745G

(17) Möbius, K.; Savitsky, A.; Lubitz, W.; Plato, M. Appl. Magn. Reson.2016, 47, 757. doi: 10.1007/s00723-016-0789-1

(18) Marcos, E.; Anglada, J. M.; Torrent-Sucarrat, M. J. Phys. Chem. C 2012, 116, 24358. doi: 10.1021/jp3083612

(19) Rosenberg, M.; Dahlstrand, C.; Kilså, K.; Ottosson, H. Chem. Rev.2014, 114, 5379. doi: 10.1021/cr300471v

(20) Ottosson, H. Nat. Chem. 2012, 4, 969. doi: 10.1038/nchem.1518

(21) Liew, J. Y.; Brown, J. J.; Moore, E. G.; Schwalbe, M. Chem. -Eur.J. 2016, 22, 16178. doi: 10.1002/chem.201602189

(22) Naskar, S.; Das, M. ACS Omega 2017, 2, 1795.doi: 10.1021/acsomega.7b00278

(23) van Leeuwen, T.; Pol, J.; Roke, D.; Wezenberg, S. J.; Feringa, B. L.Org. Lett. 2017, 19, 1402. doi: 10.1021/acs.orglett.7b00317

(24) Feixas, F.; Matito, E.; Poater, J.; Solà, M. WIREs: Comput. Mol.Sci. 2013, 3, 105. doi: 10.1002/wcms.1115

(25) Bühl, M.; Hirsch, A. Chem. Rev. 2001, 101, 1153.doi: 10.1021/cr990332q

(26) El Bakouri, O.; Duran, M.; Poater, J.; Feixas, F.; Sola, M. Phys.Chem. Chem. Phys. 2016, 18, 11700. doi: 10.1039/C5CP07011B

(27) Zhu, C. Q.; Yang, C. X.; Wang, Y. H.; Lin, G.; Yang, Y. H.; Wang,X. Y.; Zhu, J.; Chen, X. Y.; Lu, X.; Liu, G.; et al. Sci. Adv. 2016, 2,e1601031. doi: 10.1126/sciadv.1601031

(28) Ayub, R.; Bakouri, O. E.; Jorner, K.; Solà, M.; Ottosson, H. J. Org.Chem. 2017, 82, 6327. doi: 10.1021/acs.joc.7b00906

(29) Suzuki, S.; Morita, Y.; Fukui, K.; Sato, K.; Shiomi, D.; Takui, T.;Nakasuji, K. J. Am. Chem. Soc. 2006, 128, 2530.doi: 10.1021/ja058387z

(30) Chen, Z. F.; Wannere, C. S.; Corminboeuf, C.; Puchta, R.; von Ragué Schleyer, P. Chem. Rev. 2005, 105, 3842.doi: 10.1021/cr030088+

(31) Schleyer, P. v. R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N. J. R. J. Am. Chem. Soc. 1996, 118, 6317.doi: 10.1021/ja960582d

(32) Fallah-Bagher-Shaidaei, H.; Wannere, C. S.; Corminboeuf, C.;Puchta, R.; Schleyer, P. v. R. Org. Lett. 2006, 8, 863.doi: 10.1021/ol0529546

(33) Krygowski, T. M.; Szatylowicz, H.; Stasyuk, O. A.;Dominikowska, J.; Palusiak, M. Chem. Rev. 2014, 114, 6383.doi: 10.1021/cr400252h

(34) Poater, J.; Fradera, X.; Duran, M.; Solà, M. Chem. -Eur. J. 2003, 9,400. doi: 10.1002/chem.200390041

(35) Matito, E.; Duran, M.; Solà, M. J. Chem. Phys. 2005, 122, 014109.doi: 10.1063/1.1824895

(36) Hong, Y.; Oh, J.; Sung, Y. M.; Tanaka, Y.; Osuka, A.; Kim, D.Angew. Chem. Int. Ed. 2017, 56, 2932.doi: 10.1002/anie.201611431

(37) Feixas, F.; Matito, E.; Poater, J.; Solà, M. J. Comput. Chem. 2008,29, 1543. doi: 10.1002/jcc.20914

(38) Yu, D. H.; Rong, C. Y.; Lu, T.; Chattaraj, P. K.; De Proft, F.; Liu, S.B. Phys. Chem. Chem. Phys. 2017, 19, 18635.doi: 10.1039/C7CP03544F

(39) Liu, S. B. Acta Phys. -Chim. Sin. 2016, 32, 98.doi: 10.3866/PKU.WHXB201510302

(40) Liu, S. B. Acta Phys. -Chim. Sin. 2009, 25, 590.doi: 10.3866/PKU.WHXB20090332

(41) Zhao, L. L.; Grande-Aztatzi, R.; Foroutan-Nejad, C.; Ugalde, J.M.; Frenking, G. ChemistrySelect 2017, 2, 863.doi: 10.1002/slct.201602080

(42) Ciesielski, A.; Krygowski, T. M.; Cyranski, M. K.; Balaban, A. T.Phys. Chem. Chem. Phys. 2011, 13, 3737.doi: 10.1039/C0CP01446J

(43) Bernasconi, C. F.; Wenzel, P. J. J. Org. Chem. 2010, 75, 8422.doi: 10.1021/jo101719z

(44) Mo, Y. R.; Schleyer, P. v. R. Chem. -Eur. J. 2006, 12, 2009.doi: 10.1002/chem.200500376

(45) Gershoni-Poranne, R.; Stanger, A. Chem. Soc. Rev. 2015, 44, 6597.doi: 10.1039/C5CS00114E

(46) De Oliveira, B. G. Phys. Chem. Chem. Phys. 2013, 15, 37.doi: 10.1039/C2CP41749A

(47) Zhu, J.; An, K.; Schleyer, P. v. R. Org. Lett. 2013, 15, 2442.doi: 10.1021/ol400908z

(48) Cyrañski, M. K.; Krygowski, T. M.; Katritzky, A. R.; Schleyer, P.v. R. J. Org. Chem. 2002, 67, 1333. doi: 10.1021/jo016255s

(49) Krygowski, T. M.; Cyrański, M. K. Chem. Rev. 2001, 101, 1385.doi: 10.1021/cr990326u

(50) Alvarez-Thon, L.; Mammino, L. Int. J. Quantum Chem. 2017, 117,e25382. doi: 10.1002/qua.25382

(51) Karadakov, P. B.; Hearnshaw, P.; Horner, K. E. J. Org. Chem.2016, 81, 11346. doi: 10.1021/acs.joc.6b02460

(52) Boll, M.; Hilker, T. A.; Salomon, G.; Omran, A.; Nespolo, J.;Pollet, L.; Bloch, I.; Gross, C. Science 2016, 353, 1257.doi: 10.1126/science.aag1635

(53) Sundholm, D.; Fliegl, H.; Berger, R. J. F. WIREs: Comput. Mol.Sci. 2016, 6, 639. doi: 10.1002/wcms.1270

(54) Liu, S. B. J. Chem. Phys. 2007, 126, 191107.doi: 10.1063/1.2741244

(55) Liu, S. B.; Rong, C. Y.; Wu, Z. M.; Lu, T. Acta Phys. -Chim. Sin.2015, 2057. doi: 10.3866/PKU.WHXB201509183

(56) Noorizadeh, S.; Shakerzadeh, E. Comput. Theor. Chem. 2011, 964,141. doi: 10.1016/j.comptc.2010.12.012

(57) Möllerstedt, H.; Piqueras, M. C.; Crespo, R.; Ottosson, H. J. Am.Chem. Soc. 2004, 126, 13938. doi: 10.1021/ja045729c

(58) Becke, A. D. J. Chem. Phys. 1993, 98, 5648.doi: org/10.1063/1.464913

(59) Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785.doi: 10.1103/PhysRevB.37.785

(60) Francl, M. M.; Pietro, W. J.; Hehre, W. J.; Binkley, J. S.; Gordon,M. S.; DeFrees, D. J.; Pople, J. A. J. Chem. Phys. 1982, 77, 3654.doi: 10.1063/1.444267

(61) Rassolov, V. A.; Ratner, M. A.; Pople, J. A.; Redfern, P. C.; Curtiss,L. A. J. Comput. Chem. 2001, 22, 976. doi: 10.1002/jcc.1058

(62) Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.;Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.;Mennucci, B.; Petersson, G. A.; et al. Gaussian 09, Revision E. 01;Gaussian Inc.: Wallingford, CT, USA, 2013.

(63) Kudin, K. N.; Scuseria, G. E.; Cancès, E. J. Chem. Phys. 2002,116, 8255. doi: 10.1063/1.1470195

(64) Lu, T.; Chen, F. W. J. Comput. Chem. 2012, 33, 580.doi: 10.1002/jcc.22885

(65) Becke, A. D. J. Chem. Phys. 1988, 88, 2547. doi:10.1063/1.454033

(66) Richard, F.; Bader, R. Atoms in Molecules: a Quantum Theory;Oxford University Press, Oxford, UK, 1990.

(67) Hirshfeld, F. L. Theor. Chim. Acta 1977, 44, 129.doi: 10.1007/bf00549096

(68) Zhou, X. Y.; Rong, C. Y.; Lu, T.; Liu, S. B. Acta Phys. -Chim. Sin.2014, 30, 2055. doi: 10.3866/PKU.WHXB201409193

(69) Liu, S. B. J. Phys. Chem. A 2015, 119, 3107.doi: 10.1021/acs.jpca.5b00443

(70) Kohn, W.; Sham, L. J. Phys. Rev. 1965, 140, A1133.doi: 10.1103/PhysRev.140.A1133

(71) Zhao, D. B.; Rong, C. Y.; Ying, D. L.; Liu, S. B. J. Theor. Comput.Chem. 2013, 12, 1350034. doi: 10.1142/s021963361350034x

(72) Wu, W. J.; Wu, Z. M.; Rong, C. Y.; Lu, T.; Huang, Y.; Liu, S. B.J. Phys. Chem. A 2015, 119, 8216. doi: 10.1021/acs.jpca.5b04309

(73) Wu, Z. M.; Rong, C. Y.; Lu, T.; Ayers, P. W.; Liu, S. B. Phys.Chem. Chem. Phys. 2015, 17, 27052. doi: 10.1039/C5CP04442A

(74) Huang, Y.; Rong, C. Y.; Zhang, R. Q.; Liu, S. B. J. Mol. Model.2016, 23, 3. doi: 10.1007/s00894-016-3175-x

(75) Liu, S. B.; Rong, C. Y.; Lu, T. Phys. Chem. Chem. Phys. 2017, 19,1496. doi: 10.1039/C6CP06376D

(76) Zhou, X. Y.; Rong, C. Y.; Lu, T.; Zhou, P. P.; Liu, S. B. J. Phys.Chem. A 2016, 120, 3634. doi: 10.1021/acs.jpca.6b01197

(77) Noorizadeh, S.; Shakerzadeh, E. Phys. Chem. Chem. Phys. 2010,12, 4742. doi: 10.1039/B916509F

(78) Snyder, G. J. J. Phys. Chem. A 2012, 116, 5272.doi: 10.1021/jp304015k

(79) Halton, B. Eur. J. Org. Chem. 2005, 2005, 3391.doi: 10.1002/ejoc.200500231