Understanding Chemical Reactivity in Extended Systems: Exploring Models of Chemical Softness in Carbon Nanotubes

CÁRDENAS Carlos, MUÑOZ Macarena, CONTRERAS Julia, AYERS Paul W.,

GÓMEZ Tatiana6, FUENTEALBA Patricio1,2,*

1 Departamento de Fısica, Facultad de Ciencias, Universidad de Chile, Casilla, 653 Santiago, Chile.

2 Centro para el Desarrollo de la Nanociencias y Nanotecnologia, CEDENNA, Avenida Ecuador 3493, Santiago, Chile.

3 Núcleo de Matemáticas, Física y Estadística, Facultad de Ciencias, Universidad Mayor, Manuel Montt 367, Providencia,Santiago, Chile.

4 Sorbonne Universités, UPMC and CNRS, Laboratoire de Chimie Théorique (LCT), 75005 Paris, France.

5 Department of Chemistry & Chemical Biology; McMaster University; Hamilton, L8S 4M1 Ontario, Canada.

6 Institute of Applied Chemical Sciences, Theoretical and Computational Chemistry Center, Universidad Autónoma de Chile,El Llano Subercaceaux 2801, San Miguel, Santiago, Chile.

1 Introduction

When two chemical reagents approach each other both the external potentials, v(r), felt by the electrons of the reagents and the number of electrons, N, in the reagents can change.From the standpoint of the substrate, its sensitivity to these changes determines its reactivity. Specifically, if the energy of the substrate decreases (or increases relatively little) in response to the reagent’s approach, a reaction with the reagent is likely. Response functions that measure the change in energy with respect to changes in the number of electrons and changes in the external potential are thus chemical reactivity indicators.The approach to chemical reactivity theory based on these response functions is commonly called chemical (or conceptual) density-functional theory (c-DFT)1–8. A particularly important descriptor is the Fukui function, which measures the local sensitivity to the addition or removal of electrons9–15,

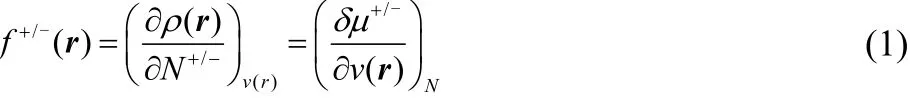
where ρ(r) is the electron density and the super-index accounts for the fact that for a finite molecule removing and adding electrons produce different responses16–21. Besides, the Fukui function can also be interpreted as the sensitivity of the chemical potential8,22–26, μ, to changes in the external potential.This change in the external potential arises because the electrons in the substrate are attracted to the nuclei and repelled by the electrons of the attacking reagent. Because the energy is a linear piecewise function of the number of electrons16–21, the Fukui functions are simply density differences,

where the density of the ions (N ± 1) has to be evaluated at the external potential of unperturbed substrate. Within the Kohn-Sham (KS) formalism, Fukui functions are frontier molecular orbitals (FMO) densities corrected by a relaxation term that takes into account the change of the KS orbitals due to the change in the number of particles of the molecule10,27,28,

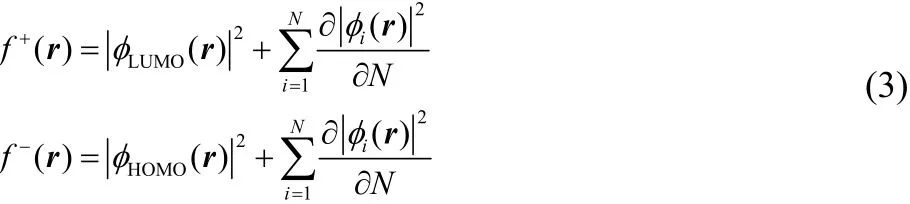
The relaxation term is expected to be important in molecules with small HOMO-LUMO gap. However, neglecting the relaxation term in Eq. (3) is a common practice because in many organic molecules empiricism seems to show that this term has either a small contribution or its contribution is more or less homogeneous in all points of the space29.

Despite the wide use of Eqs. (1)–(3), they are only valid if the ground state of the substrate and its vertical ions are nondegenerate. We have shown that Eq. (1) no longer applies for spatially-degenerate ground states because the functional derivative of the energy with respect to the external potential,(δE/v(r))Ndoes not exist in such systems and therefore the electron density of the substrate (or its ions) is not unique but it depends on the strength and the nature of the perturbation in the external potential induced by the attacking reagent. Problems can arise even if the substrate or its ions are not perfectly degenerate. If the ground state is pseudo-degenerate and the magnitude of the perturbation is large enough, the Fukui function will depend on the nature of the perturbing reagent.For describing chemical reactivity, a system should be considered pseudodegenerate if it has accessible states within an energy window comparable with the strength of the perturbation. The correct treatment of chemical reactivity for degenerate and pseudodegenerate states requires the perturbation theory of degenerate states. We have construed the theoretical framework for this situation30and have shown that the effects of degeneracies on the Fukui function31, the molecular electrostatic potential32and atomic charges33are by no means negligible.

It could be argued that spatial degeneracy of the ground state of organic compounds is uncommon. However, notice from Eq.(2) that evaluating the Fukui function requires the density not only of the “neutral” system (N) but its ions. If the ground states of these ions are (pseudo)degenerate, the Fukui cannot be evaluated from Eq. (2) either. This is easy to see in an orbital picture. Imagine a molecule whose HOMO is degenerate but the set of degenerate orbitals are fully occupied. The ground state of the molecule would be non-degenerate. However, the vertical cation is degenerate because the missing electron can be removed from any linear combination of the orbitals of the degenerate set. Then, (pseudo)degeneracy becomes important in large systems with high symmetry, such as nanostructures.This is so because symmetric systems with large numbers of atoms tend to form bands of states and to have spatially degenerate orbitals (quasiparticles states). A good example of these systems is single-wall carbon nanotubes. Depending on their diameter and chirality nanaotubes can be metals or semiconductors34,35. Describing the reactivity of metallic nanotubes is especially challenging because states around the Fermi level are pseudodegenerate. Additionally, in the case of finite single-wall capped carbon nanotubes (SWCCNT), the states around the Fermi level are usually degenerate. Consider for instance the metallic SWCCNT C360with chirality (5,5) and D5h symmetry (C360(5,5)) (cf. Scheme 1), which can be viewed as belts of hexagons with the ends capped by hemispheres of the fullerene C60. The density of KS states (DOS) computed at the LDA/3-21G level of theory is shown in Fig. 1. Notice that despite its finite size, this nanotube shows a metallic behavior that it is evident from the lack of an appreciable gap around the Fermi level (less than 0.18 eV).

Scheme 1 Capped single-wall carbon nanotube C360 with chirality(5,5) and D5h point group.

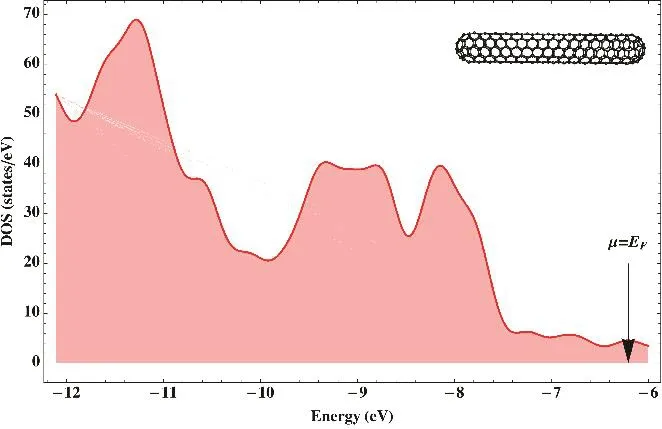
Fig. 1 Density of KS states of the capped single-wall carbon nanotube C360(5,5) computed at the LDA/3-21G level of theory.

The reactivity preferences of pristine carbon nanotubes are well known and this makes them an excellent system to test models of chemical reactivity. Pristine nanotubes are relatively inert unless they have zones of the large curvature where carbon atoms have a large deviation from the ideal sp2hybridization36,37, which implies localization of the otherwise delocalized π electrons. Thus, a model of reactivity of a metallic SWCCNT should be able to predict i) an enhanced reactivity at the ends of the tube and ii) that the reactivity rapidly decreases towards the center of the nanotube where it should become constant for long nanotubes. This last requirement arises because metals are efficient screening perturbations in the external potential and because if the nanotube is long enough, the center of it should remain unaltered by perturbations at the extremes. In other words, if a metallic system is perturbed, its chemical response should be close to nearsighted38–40. If one were to use the Fukui function of Eq. (3), one would be forced to decide which orbitals were the FMOs because HOMO and LUMO are pseudodegenerate with many states close to them (notice that there are approximately 5 states per eV around the Fermi level). When in organic molecules the density of the frontier orbital fails to describe the reactive sites, a pragmatic, but questionable,solution is to look for the closest orbital to the FMOs that describes the correct reactivity pattern. Fig. 2 shows the KS orbitals (HOMO, HOMO − 1, HOMO − 2, …, HOMO − 5) that lie within 1 eV below the Fermi Level.

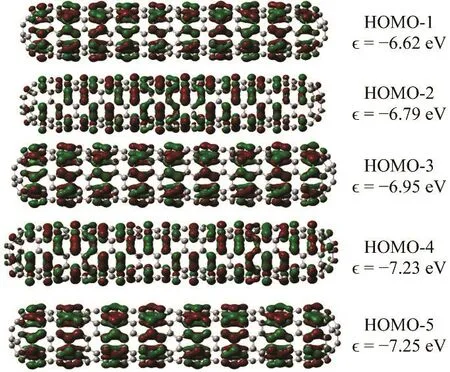
Fig. 2 Isosurface (±0.02a0−3/2) and energy of the five highest occupied KS molecular orbitals of the C360(5,5) nanotube.

It is clear that the density of none of these orbitals is able to predict the correct pattern of reactivity of the C360(5,5)nanotube because the orbitals are completely delocalized over the nanotube, resembling electrons in a cylindrical shell.Another pragmatic approach that is used when the HOMO/LUMO of a molecule is degenerate is to use the average of the densities of the set of degenerate orbitals as an approximation to the Fukui function41,42. The alleged advantage of this is that in this way the Fukui function has the same symmetry as the molecular structure; the orbital-averaged result can also be viewed as a lower bound on the true Fukui function. However, we proved that in the (pseudo)degenerate case, the chemical response does not necessarily have the symmetry of the molecule31. Fig. 3 shows this average for the last five HOMO’s, which span an energy window of 1 eV below the Fermi level. This corresponds to a strong coupling between the substrate and the reagent. Again, this strategy fails to predict the expected reactivity pattern toward electron donation. Finally, to rule relaxation effects out, we also computed the Fukui function for electron loss, f−(r), taking the difference of densities of the neutral nanotube and its cation,Eq. (2). A plot of it is shown in Fig. 4. It is clear that relaxation effects do not fix the failure of the Fukui function to explain the correct reactivity. Indeed, relaxation effects are small as it can be seen from the similarity of f−(r) and the density of the HOMO. When one computes the Fukui function as a difference of densities, one is picking what orbital the electron is leaving.But, in a pseudodegenerate system it is the nature of the perturbation that determines how orbitals around the Fermi level contribute to the electron-transfer response. We can then conclude that the Fukui function, as it is written in Eq. (1), fails to describe the correct reactivity of metallic nanotubes (and extended systems in general) because their ions are pseudodegenerate and the “contribution” of each orbital to the response is not obvious. We want to emphasize that this problem can be circumvented if the correct perturbation theory for degenerate state is used30–33. However, such treatment is complicated and computationally very expensive for systems of this size and complexity. Therefore, alternative simple models to describe the reactivity of extended systems are in order.Recently, we proposed an empirical model to weight the contribution of inner orbitals to the chemical response in which the contribution of each orbital decays exponentially with its“distance” to the Fermi level43. However, for extended systems, it seems easier to describe the chemical response in terms of the local softness, s(r), which can be written in terms of the local density of states (LDOS), g(r, E), a routinely used tool in solid state and material science11,44–46.

Fig. 3 Isosurface (4 × 10−4a0−3/2) of the five highest occupied KS molecular orbitals average density of the C360(5,5) nanotube.

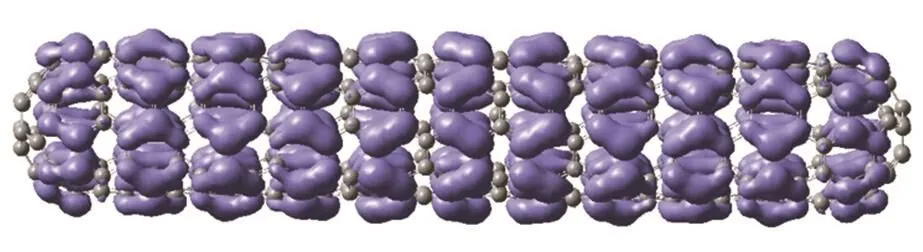
Fig. 4 Isosurface (4 × 10−4a0−3/2) of Fukui function f −(r) of the C360(5,5)

2 Models of local softness

The local softness can be interpreted as the analogous to the Fukui function but in a bath where the chemical potential is the control parameter and not the numbers of electrons (grand canonical ensemble). It measures the response of the density to variations of the chemical potential at fixed external potential while electron are free to flow between the bath and the molecule11,

The local softness at 0 K is related to the Fukui function through the global softness, S,

The main advantage of using the local softness instead of the Fukui function is that it is not necessary to add or remove electrons to evaluate the former. There is an analogous expression to Eq. (3) for the local softness in terms of the LDOS45–48, g(r, E),

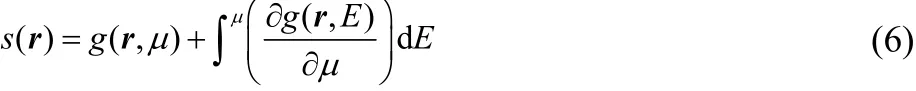
This equation was deduced by Cohen et al.7and it is based on the pioneering work by Parr and Yang11. It says that the local softness of an extended system is the local density of states at the Fermi level (at 0 K the Fermi level and the chemical potential are the same) plus a relaxation term (the integral) that accounts for the change of g(r, E) due to the fact that changing the Fermi level will change the density of occupied states. The complication in applying Eq. (6) is to have a model for the relaxation term. In a large, but still finite system, this term cannot be neglected because the result will be that the local softness is proportional to the density of the FMO(Femi level). The relaxation term is the only way that states below the Fermi level can contribute to the chemical response.As far as we know there are only two models to approximate the local softness of extended systems that try to include the relaxation contribution. Santos et al.49,50proposed to weight the local density of states by the product of the global softness and number of electrons（E ） d E ) within an arbitrary energy window, Δ, below the Fermi level,

This expression is not exactly the local softness but its chemical interpretation is similar, as they demonstrated in applications to zeolites49,51. Brommer et al.52, Geerlings et al.53,and Cardenas et al.54proposed a similar integration around the Fermi level to calculate the local softness.

Eq. (8) is inspired by the fact that the derivative in Eq. (4)can be written as the limit

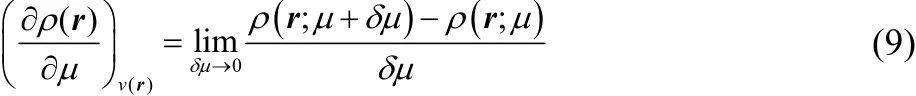
and the density is the integral of local density of states

Although Eq. (8) looks similar to the one reported by Santos et al. (Eq. (7)), the difference is that in the last model the limit for δμ is taken in order to use the smallest possible value rather than an arbitrary large window of energy below the Fermi level. Indeed, in the case of the pseudodegenerate systems, δμ should be of the order of the coupling between the external perturbation and the system (typically a fraction of an eV). sI(r)has been applied to describe the reactivity of Si(111)-(7 × 7)reconstructed surface, single wall carbon nanotubes, and alkaline earth oxides’ surfaces54. Briefly, both models (sS(r)and sI(r)) use the same basic strategy to include contributions from states below the Fermi level and, depending on the way the local density of states is calculated, they correspond to a population analysis in a portion of the valence region.Furthermore, both models weight all the states in the considered energy range equally. But, from perturbation theory one can conclude that the contribution of inner states decreases with the energetic distance to the Fermi level: the deeper the state, the smaller its contribution. For instance, the interaction energy, Eint, between the orbitals of a substrate S and the accepting state of an electrophile A (LUMO) is, at first order is given by

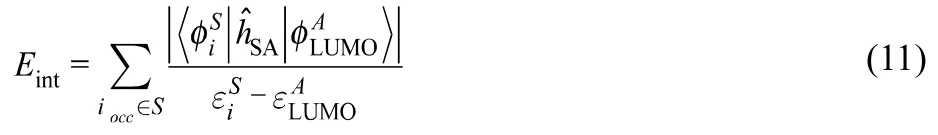
where ĥSA is the interacting Hamiltonian. Note that contribution of the inner orbitals decreases as an inverse function of the difference of energy between the orbital and the state that withdraws the electron.

A next step to improve model sI(r) is to somehow include the fact that the contribution of occupied states should decrease as their energetic distance to the Fermi level increases. To get insight on how inner states should be weighted we decided to analyze the long-range limit of the softness of a finite system through the well-known asymptotic decay of the electron density55–59,

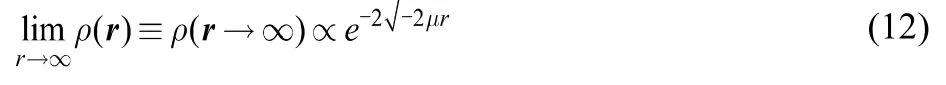
The derivative of the density with respect to the chemical potential in the long-range limit is

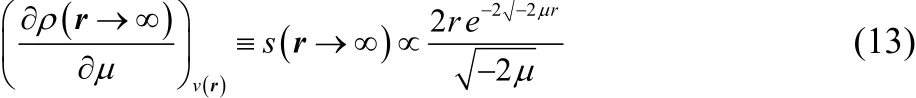
Note also that if the derivative of the density is taken not with respect to Fermi level but with respect to the energy of an inner occupied orbital, ε, the same behavior is obtained,

(This assumes that we are considering occupied orbitals defined by traditional Kohn-Sham density functional theory,with a local potential. Hartree-Fock and Generalized-Kohn-Sham occupied orbitals typically all share exactly the same rate of asymptotic decay60.)

Eqs. (13) and (14) suggest that the contribution of inner orbitals to the local softness should be weighted by the inverse of the square root of the negative of the energy of the orbital.This leads us to propose the following model for the local softness of an extended system,

In the rest of this work, we will focus on how well models sI(r) and sII(r) predict the reactivity of large metallic carbon nanotubes.

3 Computational methods

C(5,5) SWCCNTs obey a series with formula C10n+60 with alternating symmetry between D5h(n odd) and D5d(n even).The electronic structure, specifically the band gap, oscillates with a period of three belts of hexagons due to the alternation of the bonding character of the HOMO and LUMO associated with the change of symmetry35. The length at which a C(R,R)SWCCNT can be considered metallic depends on the method of calculation and Geerlings et al.53have shown that a simple Hückel (tight binding) model is enough for a qualitative treatment of the chemical reactivity of nanotubes. Within this model the molecular orbital energies are just εi= α + λiβ, where{λi} are the eigenvalues of the adjacency matrix of the Schlegel projection of the spiral code for the fullerene37. In this work,the equations were simplified by working in units of β. For evaluating the LDOS and DOS, each molecular orbital energy has been broadened as a Gaussian function with standard deviation of σ = 0.076β(0.15 eV) and the smallest δμ has been taken equal to 0.3β. Additionally, instead of reporting the local softness, we found more illustrative to use condensed-to-atoms values of it, sk61. Hence, whenever necessary, we condensed the LDOS to atoms using the Mulliken scheme62. Thus, the working equation for the softness of the k-th atom for model sII(r) is

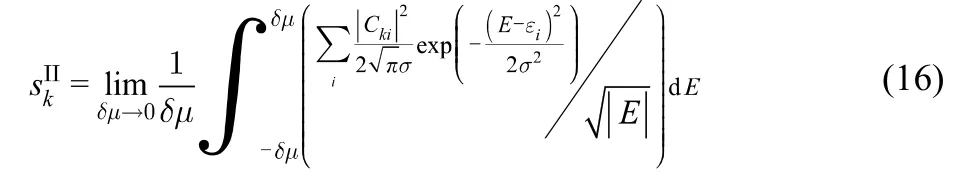
where Ckiis a the molecular orbital coefficient of the basis centered at atom k. Notice that integration limit includes states below and above the Fermi level, which has been set to E = 0.This is because in a gapless system adding and removing an infinitesimal amount of electrons can be considered equivalent processes.

4 Results and discussion

We found that the smallest C(5,5) SWCCNT with a HOMO-LUMO gap small enough to be considered metallic in the Hückel method is the C360. In order to assess the ability of the Hückel method to recover the main features of this carbon nanotube, we have plotted its DOS (cf. Fig. 5). In this plot the hopping integral β has a value 2.66 eV; this value has been deduced from the width of the valance band (3β) in the DFT calculation of Fig. 1. It is satisfactory to see that the DOS of the Hückel method has the same structure as the DFT DOS,especially in the regions of constant DOS around the Fermi level.

Fig. 6 shows the softness of the C(5,5) SWCCNT calculated by the two models sI(r) and sII(r). Due to the D5dsymmetry all atoms in a belt are equivalent. Therefore, the softness has been plotted as a function of the belt number. We will focus first in the sidewall of the nanotube (belts 5–35). Both models predict an oscillatory character with a period of three belts, with the average softness decreasing towards the center of the nanotube.However, for model sI(r) this decrease is quite slow while in model sII(r) the softness becomes almost constant after the 8th belt measured from the union of the sidewall and the caps.Indeed, given the nearsighted character of the softness kernel40,one should expect that in a metallic capped nanotube, the reactivity in the center of the nanotube is smaller and almost independent of the position. In this sense, weighting the contribution of occupied states below the Fermi level, as done in sII(r), becomes essential for describing the right trend of reactivity far from the ends of the nanotube. The slow decaying oscillations in model sI(r) could be, however, caused by the finite size of the C(5,5) nanotube. Now we move to reactivity at the ends of the nanotube. Note that model sI(r) predicts that the most reactive sites of the nanotube are those corresponding to the union of the caps to the cylinder shell, which is expected because those atoms present a large deviation of the ideal sp2hybridization of the graphene sheet. However, notice that the sI(r) model totally fails in predicting that the other atoms in the caps also have enhanced reactivity. In indeed, model sI(r)predicts that the outermost pentagonal belt of the nanotube is the least reactive. On the contrary, model sII(r) correctly predicts that all the atoms in the caps are the most reactive and that the outermost pentagonal belt along with the belt where the sidewall and the cap merge contains the most reactive sites.That is, only the model in which the contribution of inner orbitals to the chemical response is weighted according to how deep below the Fermi level these state lay is able to provide a satisfactory picture of the chemical reactivity of capped metallic carbon nanotubes (Fig. 6, bottom panel).

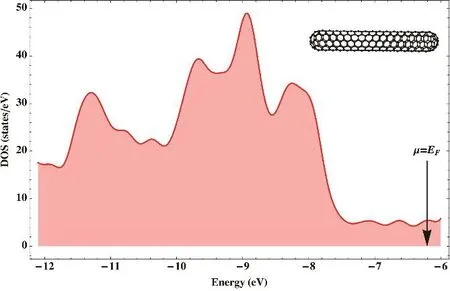
Fig. 5 Density of Hückel states of the capped single-wall carbon nanotube C360(5,5) computed with a hopping integral β = 2.66 eV.

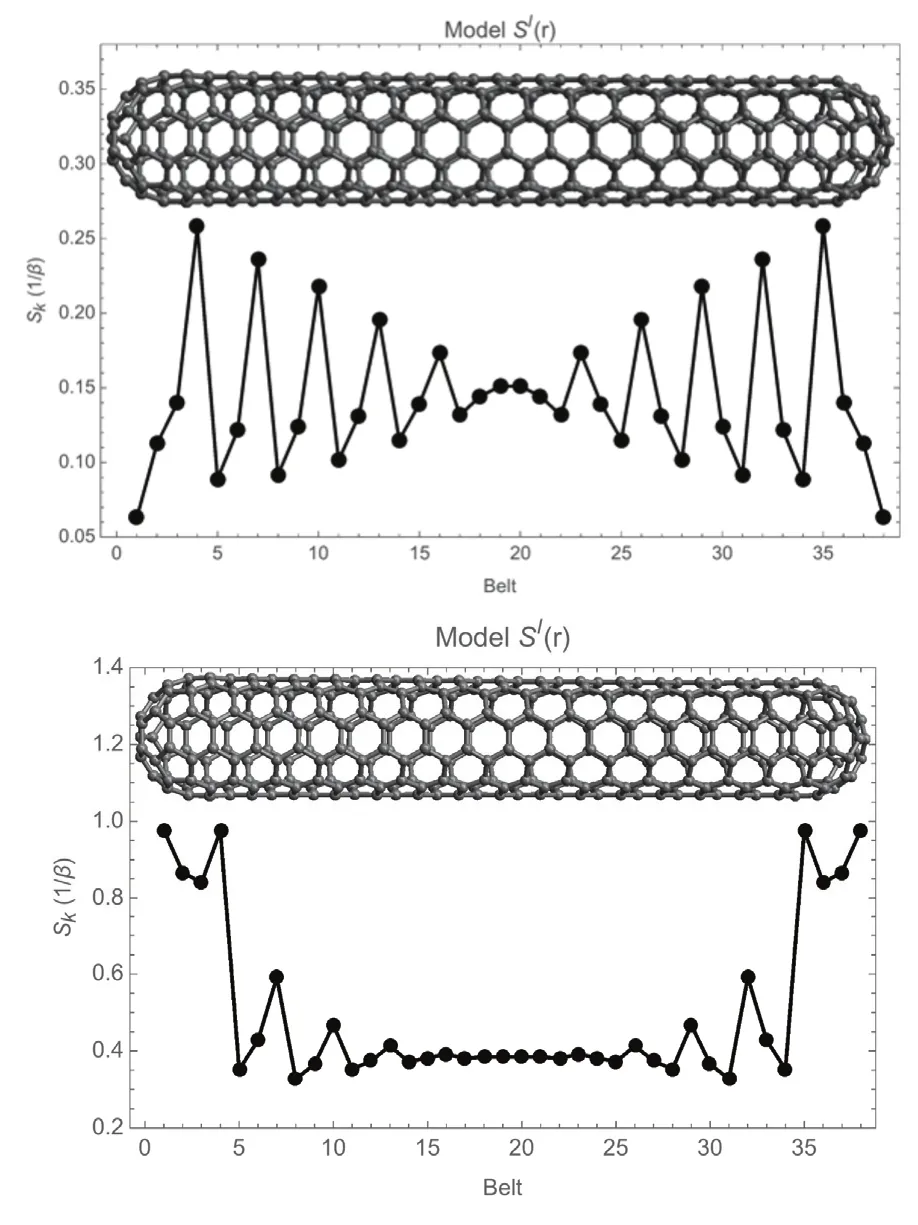
Fig. 6 Condensed-to-atoms local softness of capped single-wall carbon nanotube C360(5,5) evaluated with a model, s I(r), that equally weights the contribution of all states (top) and, a model, s II(r), that weights the contribution of inner states according to how deep below the Fermi they lay (bottom).

5 Conclusions

It is an established rule of chemical physics that the most reactive sites of a molecule toward electron donation/acceptance are those where the frontier-orbital density is high.When a molecule changes its number of electrons due to the approach of a reagent, the chemical response is characterized by the Fukui function. However, if the system or its ions are degenerate or pseudodegenerate, the Fukui function is not well defined because it depends on the detailed nature of the perturbation and, in the case of quasidegeneracy, it includes contributions from non-frontier states. The correct way to treat such a system would be to use the perturbation theory of degenerated states to evaluate the chemical response, but such a treatment is mathematically complicated and, for extended systems, computationally expensive. This is particularly problematic because (pseudo)degeneracy is ubiquitous in extended (even infinite) systems. This motivated the simple models we explore in this work. In particular, using this work we proposed a model of local softness sII(r), based on the local density of states, in which the contribution to the chemical reactivity of states lying below/above the frontier state is included. The way this contribution is weighted is taken from the long-range (asymptotic) decay of the local softness. We implemented this model, along with a previously proposed one in which all states are equally weighted52–54, sI(r), for single-wall carbon nanotubes. Pristine carbon nanotubes are an excellent test system because their reactivity is known to depend on the local curvature of the structure and because many of their electronic structure features are captured by a Hückel Hamiltonian. We showed that model sII(r), but not model sI(r), successfully explains the reactivity of both the sidewalls and the ends of capped nanotubes. This establishes the importance of weighting inner states appropriately, ideally based on physical, rather than ad hoc, arguments. Finally, we think that the type of model discussed here opens new ways to characterize the reactivity of more complex systems like surfaces and nanoparticles.

(1) Parr, R. G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford UP: New York, NY, USA, 1989.

(2) Geerlings, P.; De Proft, F.; Langenaeker, W. Chem. Rev. 2003, 103,1793. doi: 10.1021/cr990029p

(3) Chermette, H. J. Comput. Chem. 1999, 20, 129.doi: 10.1002/(SICI)1096-987X(19990115)20:1

(4) Liu, S. B. Acta Phys. -Chim. Sin. 2009, 25, 590.doi: 10.3866/PKU.WHXB20090332

(5) Gazquez, J. L. J. Mex. Chem. Soc. 2008, 52, 3.

(6) Ayers, P. W.; Anderson, J. S. M.; Bartolotti, L. J. Int. J. Quantum Chem. 2005, 101, 520. doi: 10.1002/qua.20307

(7) Chattaraj, P. K.; Sarkar, U.; Roy, D. R. Chem. Rev. 2006, 106, 2065.doi: 10.1021/cr040109f

(8) Johnson, P. A.; Bartolotti, L. J.; Ayers, P. W.; Fievez, T.; Geerlings,P. Modern Charge-Density Analysis; Springer: The Netherlands,2012; p. 715.

(9) Parr, R. G.; Yang, W. T. J. Am. Chem. Soc. 1984, 106, 4049.doi: 10.1021/ja00326a036

(10) Yang, W. T.; Parr, R. G.; Pucci, R. J. Chem. Phys. 1984, 81, 2862.doi: 10.1063/1.447964

(11) Yang, W. T.; Parr, R. G. Proc. Natl. Acad. Sci. USA 1985, 82, 6723.doi: 10.1073/pnas.82.20.6723

(12) Fukui, K. Science 1982, 218, 747.doi: 10.1126/science.218.4574.747

(13) Ayers, P. W.; Levy, M. Theo. Chem. Acc. 2000, 103, 353.doi: 10.1007/s002149900093

(14) Fuentealba, P.; Cardenas, C.; Pino-Rios, R.; Tiznado, W.Applications of Topological Methods in Molecular Chemistry;Springer International Publishing: Switzerland, 2016; p. 227.

(15) Ayers, P. W.; Yang, W. T.; Bartolotti, L. J. Chemical Reactivity Theory: A Density Functional View; Chattaraj, P. K., Ed.; CRC Press:Boca Raton, FL, USA, 2009; p. 255.

(16) Perdew, J. P.; Parr, R. G.; Levy, M.; Balduz, J. L., Jr. Phys. Rev. Lett.1982, 49, 1691. doi: 10.1103/PhysRevLett.49.1691

(17) Chan, G. K. L. J. Chem. Phys. 1999, 110, 4710.doi: 10.1063/1.478357

(18) Yang, W. T.; Zhang, Y. K.; Ayers, P. W. Phys. Rev. Lett. 2000, 84,5172. doi: 10.1103/PhysRevLett.84.5172

(19) Cohen, M. H.; Wasserman, A. Isr. J. Chem. 2003, 43, 219.doi: 10.1560/3R9J-FHB5-51UV-C4BJ

(20) Ayers, P. W. J. Math. Chem. 2008, 43, 285.doi: 10.1007/s10910-006-9195-5

(21) Cohen, A. J.; Mori-Sanchez, P.; Yang, W. T. Science 2008, 321, 792.doi: 10.1126/science.1158722

(22) Parr, R. G.; Donnelly, R. A.; Levy, M.; Palke, W. E. J. Chem. Phys.1978, 68, 3801. doi: 10.1063/1.436185

(23) Nalewajski, R. F.; Kozlowski, P. M. Acta Phys. Polon. 1986, A70,457.

(24) Cárdenas, C.; Heidar-Zadeh, F.; Ayers, P. W. Phys. Chem. Chem.Phys. 2016, 18, 25721. doi: 10.1039/C6CP04533B

(25) Sablon, N.; De Proft, F.; Ayers, P. W.; Geerlings, P. J. Chem. Phys.2007, 126, 224108. doi: 224108/Artn 224108

(26) Fievez, T.; Sablon, N.; De Proft, F.; Ayers, P. W.; Geerlings, P.J. Chem. Theory Comput. 2008, 4, 1065. doi: 10.1021/ct800027e

(27) Fuentealba, P.; Chamorro, E.; Cárdenas, C. Int. J. Quantum Chem.2007, 107, 37. doi: 10.1002/qua.21021

(28) Bartolotti, L. J.; Ayers, P. W. J. Phys. Chem. A 2005, 109, 1146.doi: 10.1021/jp0462207

(29) Echegaray, E.; Rabi, S.; Cardenas, C.; Zadeh, F. H.; Rabi, N.; Lee, S.;Anderson, J. S.; Toro-Labbe, A.; Ayers, P. W. J. Mol. Model. 2014,20, 1. doi: 10.1007/s00894-014-2162-3

(30) Cardenas, C.; Ayers, P. W.; Cedillo, A. J. Chem. Phys. 2011, 134,174103. doi: 10.1063/1.3585610

(31) Bultinck, P.; Cardenas, C.; Fuentealba, P.; Johnson, P. A.; Ayers, P.W. J. Chem. Theory Comput. 2013, 10, 202. doi: 10.1021/ct400874d

(32) Bultinck, P.; Cardenas, C.; Fuentealba, P.; Johnson, P. A.; Ayers, P.W. J. Chem. Theory Comput. 2013, 9, 4779. doi: 10.1021/ct4005454

(33) Bultinck, P.; Jayatilaka, D.; Cardenas, C. Comput. Theor. Chem. 2015,1053, 106. doi: 10.1016/j.comptc.2014.06.017

(34) Avouris, P. Accounts Chem. Res. 2002, 35, 1026.doi: 10.1021/ar010152e

(35) Fowler, P. W.; Manopoulos, D. E. An Atlas of Fullerene; Oxford Press University: Oxford, UK, 1995.

(36) Banerjee, S.; Hemraj-Benny, T.; Wong, S. S. Adv. Mater. 2005, 17,17. doi: 10.1002/adma.200401340

(37) Fowler, P. W. Contemp. Phys. 1996, 37, 235.doi: 10.1080/00107519608217530

(38) Prodan, E.; Kohn, W. Proc. Natl. Acad. Sci. USA 2005, 102, 11635.doi: 10.1073/pnas.0505436102

(39) Prodan, E. Phys. Rev. B 2006, 73, 085108.doi: 10.1103/PhysRevB.73.085108

(40) Cardenas, C.; Rabi, N.; Ayers, P. W.; Morell, C.; Jaramillo, P.;Fuentealba, P. J. Phys. Chem. A 2009, 113, 8660.doi: 10.1021/jp902792n

(41) Flores-Moreno, R. J. Chem. Theory Comput. 2009, 6, 48.doi: 10.1021/ct9002527

(42) Martínez, J. Chem. Phys. Lett. 2009, 478, 310.doi: 10.1016/j.cplett.2009.07.086

(43) Pino-Rios, R.; Yañez, O.; Inostroza, D.; Ruiz, L.; Cardenas, C.;Fuentealba, P.; Tiznado, W. J. Comput. Chem. 2017, 38, 481.doi: 10.1002/jcc.24699

(44) Berkowitz, M.; Parr, R. G. J. Chem. Phys. 1988, 88, 2554.doi: 10.1063/1.454034

(45) Cohen, M. H.; Ganduglia-Pirovano, M. V. J. Chem. Phys. 1994, 101,8988. doi: 10.1063/1.468026

(46) Cohen, M. H.; Ganduglia-Pirovano, M. V.; Kudrnovsky, J. J. Chem.Phys. 1995, 103, 3543. doi: 10.1063/1.470238

(47) Cohen, M. H.; Ganduglia-Pirovano, M. V.; Kudrnovsky, J. Phys. Rev.Lett. 1994, 72, 3222. doi: 10.1103/PhysRevLett.72.3222

(48) Cohen, M. H. Top. Curr. Chem. Density Functional Theory IV;Springer-Verlag, Berlin, Germany, 1996; Vol. 183, p. 143.

(49) Santos, J. C.; Contreras, R.; Chamorro, E.; Fuentealba, P. J. Chem.Phys. 2002, 116, 4311. doi: 10.1063/1.1449944

(50) Alzate-Morales, J. H.; Tiznado, W.; Santos, J. C.; Cardenas, C.;Contreras, R. J. Phys. Chem. B 2007, 111, 3293.doi: 10.1021/jp064549h

(51) Santos, J. C.; Chamorro, E.; Contreras, R.; Fuentealba, P. Chem. Phys.Lett. 2004, 383, 612. doi: 10.1016/j.cplett.2003.11.083

(52) Brommer, K. D.; Galván, M.; Dal Pino, A.; Joannopoulos, J. D. Surf.Sci. 1994, 314, 57. doi: 10.1016/0039-6028(94)90212-7

(53) Nguyen, L. T.; De Proft, F.; Amat, M. C.; Van Lier, G.; Fowler, P.W.; Geerlings, P. J. Phys. Chem. A 2003, 107, 6837.doi: 10.1021/jp034388

(54) Cardenas, C.; De Proft, F.; Chamorro, E.; Fuentealba, P.; Geerlings, P.J. Chem. Phys. 2008, 128, 034708. doi: 10.1063/1.2819239

(55) Morrell, M. M.; Parr, R. G.; Levy, M. J. Chem. Phys. 1975, 62, 549.doi: 10.1063/1.430509

(56) Katriel, J.; Davidson, E. R. Proc. Natl. Acad. Sci. USA 1980, 77,4403. doi: 10.1073/pnas.77.8.4403

(57) Hoffmann-Ostenhof, M.; Hoffmann-Ostenhof, T. Phys. Rev. A 1977,16, 1782. doi: 10.1103/PhysRevA.16.1782

(58) Ahlrichs, R.; Hoffmann-Ostenhof, M.; Hoffmann-Ostenhof, T.;Morgan, J. D., III. Phys. Rev. A 1981, 23, 2106.doi: 10.1103/PhysRevA.23.2106

(59) Levy, M.; Perdew, J. P.; Sahni, V. Phys. Rev. A 1984, 30, 2745.doi: 10.1103/PhysRevA.30.2745

(60) Handy, N. C.; Marron, M. T.; Silverstone, H. J. Phys. Rev. 1969, 180,45. doi: 10.1103/PhysRev.180.45

(61) Yang, W. T.; Mortier, W. J. J. Am. Chem. Soc. 1986, 108, 5708.doi: 10.1021/ja00279a008

(62) Mulliken, R. S. J. Chem. Phys. 1955, 23, 1833.doi: 10.1063/1.1740588