Levy Constrained Search in Fock Space:An Alternative Approach to Noninteger Electron Number

AYERS Paul W. , LEVY Mel

1 Department of Chemistry and Chemical Biology, McMaster University, Hamilton, Ontario L8S 4M1, Canada.

2 Department of Physics, North Carolina A&T State University, Greensboro, NC 27411, USA.

3 Department of Chemistry, Duke University, Durham, NC 27708, USA.

4 Department of Chemistry, Tulane University, New Orleans, LA 70118, USA.

1 Motivation

In the density functional theory of molecular electronic structure, the electron density replaces the many-electron wavefunction as the fundamental descriptor of an electronic system1–5. The variational principle for the N-electron wavefunction

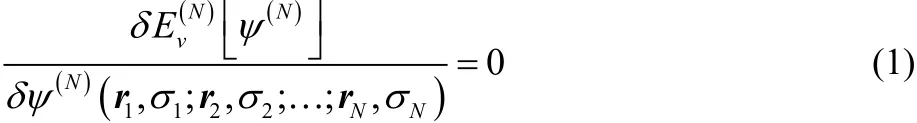
can be used to find the ground state and also all of the stationary excited states of the system. Here,

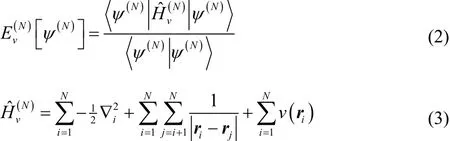
anddenote the spatial position and spin of the N electrons.

The corresponding variational principle for the electron density1,5,

where

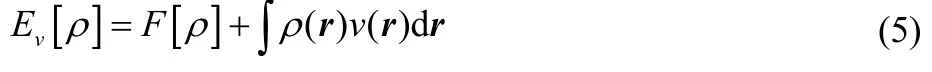
and in this paper we will choose to consider the Levy constrained search functional5,6,

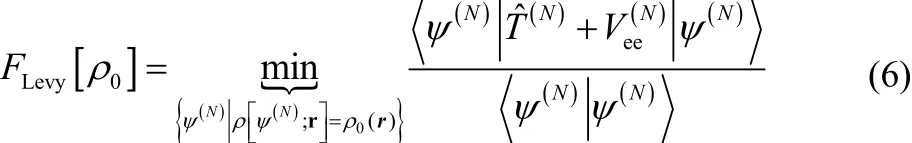
The notation in Eq. (6) means that one minimizes the expectation value of the sum of the kinetic and electron-electron repulsion energies,

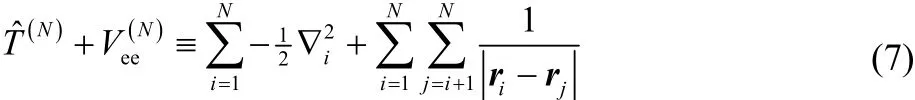
with respect to all wavefunctions that give the target electron density,

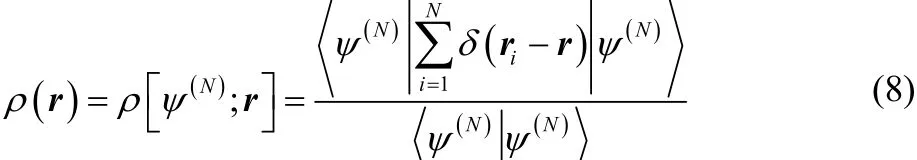
Eq. (4) can be used to find the ground-state of the system and, for systems with more than one electron, at most a few excited states of the system7. Note that by choosing a different functional form in Eq. (6) (e.g., a bifunctional), excited-states are accessible from the fundamental variational principle, Eq.(4)8–21,22.

Eq. (4) presents a fundamental difficulty: an infinitesimal change in the electron density only at the point r will induce an infinitesimal change in the number of electrons, but the Levy constrained search functional, Eq. (6), is defined only for electron densities with integer electron number. In density functional theory, one is thus impelled to extend the domain of F[ρ] to include electron densities with noninteger electron number. This can be done in several ways: using the grand canonical ensemble23,24, making mathematical arguments based on size-consistency, etc.25,26. While the need to consider“nonphysical” systems with the noninteger electron number seems inconvenient at first, it turns out to be useful conceptually2,27–34, and is one reason that the discipline known as conceptual density functional theory has had such great success at describing electron-transfer processes in chemistry like acid/base reactions35–39.

2 The Levy constrained search in Fock space

The goal of this paper is to show that the Levy wavefunction constrained search can be extended to densities with noninteger electron number, and that the resulting functional is identical(for ground state densities) to the zero-temperature grand-canonical ensemble constrained search. This is a result that has been known to these authors for some time (since at least the late 1990s) but which seemingly has not been previously published.

The approach is simple. Any wavefunction in Fock space40–45can be written as,

where ψ（N）is an N-electron wavefunction (with integer N).The electron number operator is a symmetry of the system in the sense that it commutes with the Hamiltonian in Fock space;this means that wavefunctions with different electron number are orthogonal. For simplicity, henceforth we shall assume that the ψ（N）for each specific electron number are normalized to unity, so that:

The expectation value for the energy, the number of electrons, and the electron density in Fock space are then,respectively, ψ

As usual, the electron density is normalized to the number of electrons,

The Levy constrained search in Fock space is defined as

It is straightforward to see that this functional is exact. Using the variational principle in Fock space,

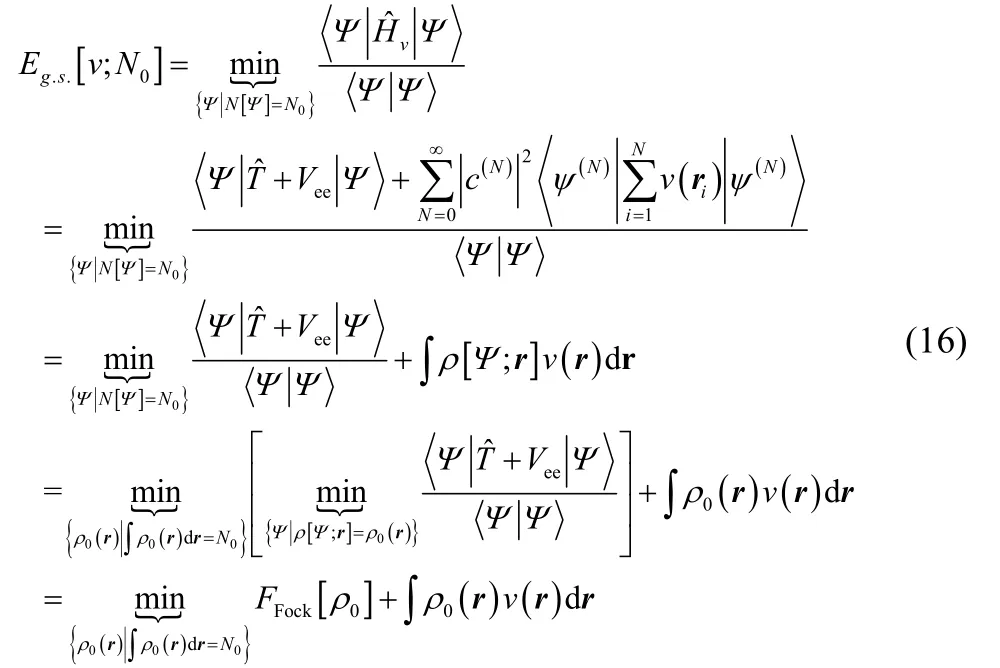
The last line indicates that if a density other than the ground-state electron density is used, an upper bound to the true ground-state energy is obtained.

For integer electron number, FFock[ρ] is a lower bound to the traditional fixed-N wavefunction constrained search. More generally, F Fock[ρ] ≤ F Levy[ρ]. This is clear from the fact that the variational space in Eq. (15) is larger than it is in Eq. (6). For example, a 10-electron density can be constructed as

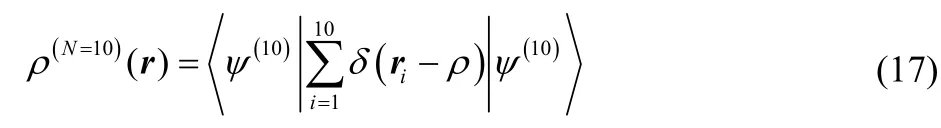
or as

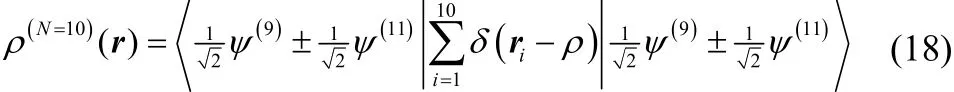
Only Eq. (17) is included in the traditional Levy constrained search, while both Eqs. (17) and (18) are included in its Fock-space generalization.

For ground-state systems with noninteger electron number,FFock[ρ] gives the same energy as obtained using the zero-temperature grand canonical ensemble approach. To see this, we use the equivalence

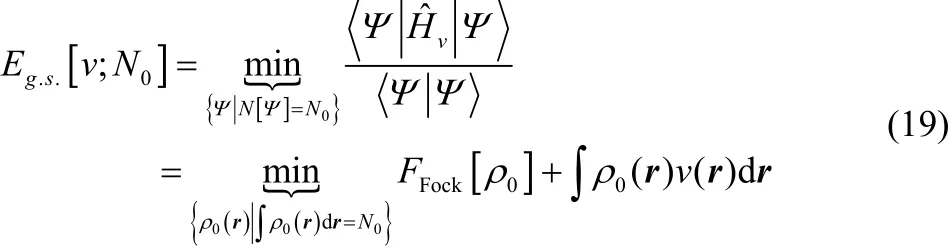
For convenience, we expandin terms of the N-electron eigenfunctions ofTherefore,

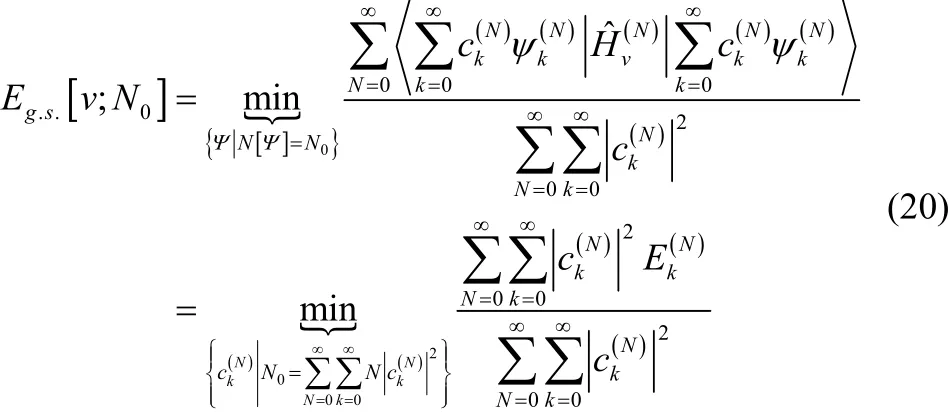
A reader familiar with the zero-temperature grand canonical ensemble will recognize that Eq. (20) is equivalent to the expectation value for the electronic energy in that approach23,24,46–57. For completeness, however, we will simplify the expression in Eq. (20). First, note that mixing in contributions from N-electron excited states always increases the energy. Therefore,

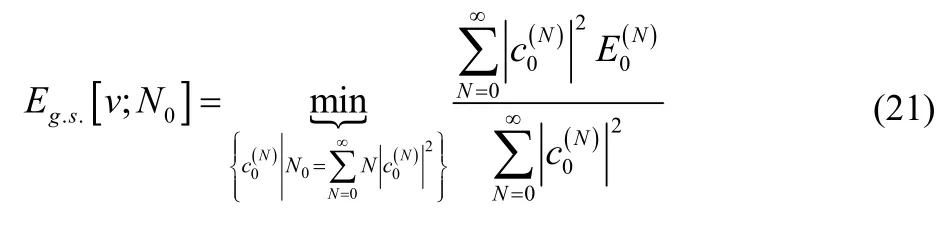
Next we assume that the energy is strictly convex with respect to the number of electrons. (Henceforth we will call this N-convexity.) That is, for systems with an integer number of electrons, N,

Eq. (22) is believed to be true for all Coulomb systems, but it has never been proved. The minimum in Eq. (21) then occurs when

where [N0] and [N0] denote the floor and ceiling functions,respectively. (e.g.,3 7 and3 8.) The energy expression is therefore

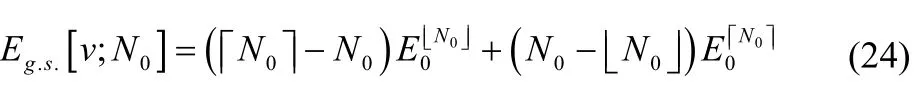
This is the mathematical representation of the “straight-line interpolation” that is obtained when one rigorously describes the ground state of a system with noninteger electron number.Notice that by differentiating Eq. (24) with respect to the external potential, one finds that the electron density23,58and its response functions34are also linearly interpolated between their values at the integers. The same interpolation, in fact,occurs for most molecular properties26.

When the energy is not N-convex, the N0-electron ground state energy of the system with external potential v(r),

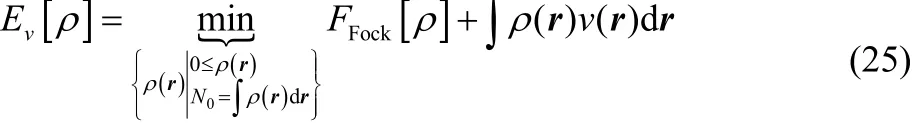
is still identical to the result from the grand canonical ensemble. When N-convexity is not true, there exists two nonnegative integers, k and l, such that

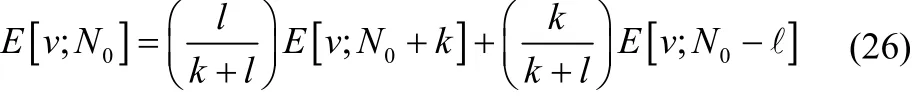
This mixed-N-state is a pure state in Fock space, with the wavefunction,

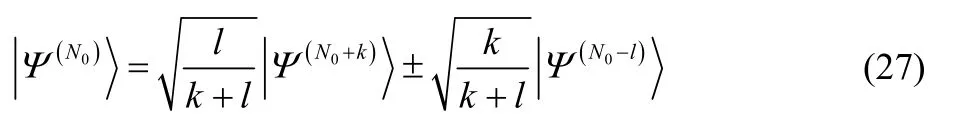
In general, a mixture of pure states from different electron numbers is a pure state in Fock space. While FFock[ρ] is identical to the zero-temperature grand canonical ensemble for electronic ground states, it does have advantages for the treatment of excited states. Like the fixed-N ensemble constrained search59, the grand canonical ensemble functional is a convex function of the electron density. (To avoid confusion with N-convexity, we call this ρ-convexity.) Like the conventional fixed-N Levy constrained search, FFock[ρ] is not convex. This means that FFock[ρ] can be used to study excited-state electron densities.

Specifically, suppose that(r) is an eigendensity for an excited state of the Fock-space Hamiltonian Hˆvand that it is not a ground-state v-representable density. Suppose furthermore that when one performs the constrained search, that the wavefunction one finds is an eigenfunction,HˆvΨk=EkΨk,

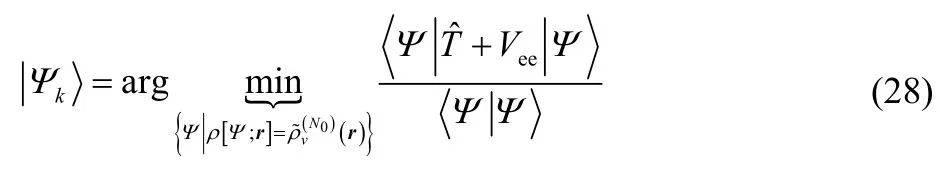
Then

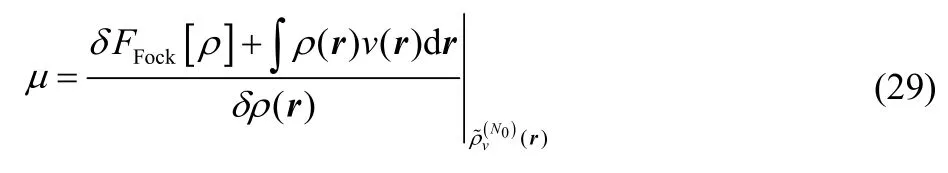
This is true by the same argument Perdew and Levy made in Ref. 7. Intuitively, one can derive it using the chain rule.Restricting oneself to density variations that preserve electron number, one may write,

but the first term in the integral is zero because the Fock-space Levy constrained search recovers an excited-state eigenfunction for the system, and so infinitesimal variations of that wavefunction fail to alter the energy.

3 Summary

We extended the Levy wavefunction constrained search to Fock space wavefunctions,

defining

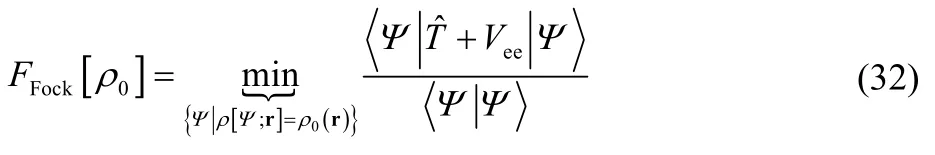
This functional is exact and variational; it gives the same results as the zero-temperature grand-canonical ensemble constrained search functional for ground states of electronic systems with any number of electrons, including nonintegers.One potential advantage of this functional is that it can give exact results for certain excited states because it, like the fixed-N Levy constrained search (Eq. (6)) is not ρ-convex. In general, FFock[ρ] ≤ FLevy[ρ]. However, FFock[ρ] = FLevy[ρ] for pure-state v-representable densities whenever the electronic energy is a convex function of the number of electrons.

Acknowledgment:PWA thanks Compute Canada,NSERC, and the Canada Research Chairs for research support.

(1) Hohenberg, P.; Kohn, W. Phys. Rev. 1964, 136, B864.doi: 10.1103/PhysRev.136.B864

(2) Parr, R. G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford UP: New York, NY, USA, 1989.

(3) Kohn, W.; Becke, A. D.; Parr, R. G. J. Phys. Chem. 1996, 100,12974. doi: 10.1021/jp960669l

(4) Kohn, W. Rev. Mod. Phys. 1999, 71, 1253.doi: 10.1103/RevModPhys.71.1253

(5) Levy, M. Proc. Natl. Acad. Sci. USA 1979, 76, 6062.doi: 10.1073/pnas.76.12.6062

(6) Levy, M.; Perdew, J. P. The Constrained Search Formulation of Density Functional Theory. In Density Functional Methods in Physics, NATO ASI Series (Series B: Physics), Vol. 123; Dreizler, R.M., da Providência, J. Eds.; Springer: Boston, MA, USA.doi: 10.1007/978-1-4757-0818-9_2

(7) Perdew, J. P.; Levy, M. Phys. Rev. B 1985, 31, 6264.doi: 10.1103/PhysRevB.31.6264

(8) Gorling, A. Phys. Rev. A 1996, 54, 3912.doi: 10.1103/PhysRevA.54.3912

(9) Gorling, A. Phys. Rev. A 1999, 59, 3359.doi: 10.1103/PhysRevA.59.3359

(10) Levy, M. In On Time-Independent Density-Functional Theories for Excited States, Proceedings of the 1st International Workshop Electron Correlation and Material Properties, 1999;pp. 299–308.

(11) Levy, M.; Nagy, A. Phys. Rev. Lett. 1999, 83, 4361.doi: 10.1103/PhysRevLett.83.4361

(12) Levy, M.; Nagy, A. Phys. Rev. A 1999, 59, 1687.doi: 10.1103/PhysRevA.59.1687

(13) Nagy, A.; Levy, M. Phys. Rev. A 2001, 63, 052502.doi: 10.1103/PhysRevA.63.052502

(14) Nagy, A.; Levy, M.; Ayers, P. W. Time-Independent Theory for a Single Excited State. In Chemical Reactivity Theory: A Density Functional View; Chattaraj, P. K., Ed.; Taylor and Francis: Boca Raton, FL, USA, 2009; p. 121.

(15) Ayers, P. W.; Levy, M. Phys. Rev. A 2009, 80, 012508.doi: 10.1103/PhysRevA.80.012508

(16) Ayers, P. W.; Nagy, A.; Levy, M. Phys. Rev. A 2012, 85, 042518.doi: 10.1103/PhysRevA.85.042518

(17) Ayers, P. W.; Levy, M.; Nagy, A. J. Chem. Phys. 2015, 143 (19), 4.doi: 10.1063/1.4934963

(18) Evangelista, F. A.; Shushkov, P.; Tully, J. C. J. Phys. Chem. A 2013,117 (32), 7378. doi: 10.1021/jp401323d

(19) Glushkov, V. N.; Assfeld, X. J. Chem. Phys. 2010, 132, 204106.doi: 10.1063/1.3443777

(20) Glushkov, V. N.; Levy, M. J. Chem. Phys. 2007, 126, 174106.doi: 10.1063/1.2733657

(21) Miranda-Quintana, R. A.; Gonzalez, M. M. Int. J. Quantum Chem.2013, 113 (22), 2478. doi: 10.1002/qua.24486

(22) Ayers, P. W. Variational Principles for Understanding Chemical Reactions. Ph.D. Dissertation, University of North Carolina: Chapel Hill, NV, USA, 2001.

(23) Perdew, J. P.; Parr, R. G.; Levy, M.; Balduz, J. L., Jr. Phys. Rev. Lett.1982, 49, 1691. doi: 10.1103/PhysRevLett.49.1691

(24) Zhang, Y. K.; Yang, W. T. Theor. Chem. Acc. 2000, 103, 346.doi: 10.1007/s002149900021

(25) Yang, W. T.; Zhang, Y. K.; Ayers, P. W. Phys. Rev. Lett. 2000, 84,5172. doi: 10.1103/PhysRevLett.84.5172

(26) Ayers, P. W. J. Math. Chem. 2008, 43, 285.doi: 10.1007/s10910-006-9195-5

(27) Liu, S. B. Acta Phys. -Chim. Sin. 2009, 25, 590.doi: 10.3866/PKU.WHXB20090332

(28) Ayers, P. W.; Anderson, J. S. M.; Bartolotti, L. J. Int. J. Quantum Chem. 2005, 101, 520. doi: 10.1002/qua.20307

(29) Johnson, P. A.; Bartolotti, L. J.; Ayers, P. W.; Fievez, T.; Geerlings,P. Charge Density and Chemical Reactivity: A Unified View from Conceptual DFT. In Modern Charge Density Analysis; Gatti, C.,Macchi, P. Eds.; Springer: New York, NY, USA, 2012; pp. 715–764.

(30) De Proft, F.; Geerlings, P.; Ayers, P. W. The conceptual Density Functional Theory Perspective of Bonding. In The Chemical Bond:Fundamental Aspects of Chemical Bonding; Shaik, S., Frenking, G.,Eds.; Wiley: Darmstadt, Germany, 2014; Vol. 1, pp. 233–270.

(31) Gazquez, J. L. J. Mex. Chem. Soc. 2008, 52, 3.

(32) Geerlings, P.; De Proft, F.; Langenaeker, W. Chem. Rev. 2003, 103,1793. doi: 10.1021/cr990029p

(33) Heidar-Zadeh, F.; Miranda-Quintana, R. A.; Verstraelen, T.;Bultinck, P.; Ayers, P. W. J. Chem. Theory Comp. 2016, 12 (12),5777. doi: 10.1021/acs.jctc.6b00494

(34) Heidar-Zadeh, F.; Richer, M.; Fias, S.; Miranda-Quintana, R. A.;Chan, M.; Franco-Perez, M.; Gonzalez-Espinoza, C. E.; Kim, T. D.;Lanssens, C.; Patel, A. H. G.; et al. Chem. Phys. Lett. 2016, 660, 307.doi: 10.1016/j.cplett.2016.07.039

(35) Liu, S. B.; Schauer, C. K.; Pedersen, L. G. J. Chem. Phys. 2009, 131,164107. doi: 10.1063/1.3251124

(36) Ayers, P. W.; Parr, R. G.; Pearson, R. G. J. Chem. Phys. 2006, 124,194107. doi: 10.1063/1.2196882

(37) Chattaraj, P. K.; Ayers, P. W.; Melin, J. Phys. Chem. Chem. Phys.2007, 9, 3853. doi: 10.1039/b705742c

(38) Ayers, P. W. Faraday Discuss. 2007, 135, 161.doi: 10.1039/b606877d

(39) Chattaraj, P. K.; Ayers, P. W. J. Chem. Phys. 2005, 123, 086101.doi: 10.1063/1.2011395

(40) Kutzelnigg, W. J. Chem. Phys. 1985, 82 (9), 4166.doi: 10.1063/1.448859

(41) Kutzelnigg, W.; Koch, S. J. Chem. Phys. 1983, 79 (9), 4315.doi: 10.1063/1.446313

(42) Kutzelnigg, W. J. Chem. Phys. 1982, 77 (6), 3081.doi: 10.1063/1.444231

(43) Kutzelnigg, W. Quantum chemistry In Fock Space. In Aspects of Many-Body Effects in Molecules and Extended Systems; Mukherjee,D., Ed.; Springer-Verlag: Berlin, Germany,1989; pp. 35–68.

(44) Kutzelnigg, W. J. Chem. Phys. 1984, 80 (2), 822.doi: 10.1063/1.446736

(45) Stone, M. H. Linear Transformations in Hilbert Space; American Mathematical Society: New York, NY, USA, 1932; Vol. 15.

(46) Eschrig, H. The Fundamentals of Density Functional Theory. Eagle:Leipzig, Germany, 2003.

(47) Eschrig, H. Phys. Rev. B 2010, 82, 205120.doi: 10.1103/PhysRevB.82.205120

(48) Malek, A. M.; Balawender, R. ar Xiv:1310.6918 2013.

(49) Malek, A.; Balawender, R. J. Chem. Phys. 2015, 142. 054104.doi: 10.1063/1.4906555

(50) Franco-Perez, M.; Ayers, P. W.; Gazquez, J. L. Theor. Chem. Acc.2016, 135 (8), 199. doi: 10.1007/s00214-016-1961-2

(51) Franco-Perez, M.; Ayers, P. W.; Gazquez, J. L.; Vela, A. J. Chem.Phys. 2015, 143 (24), 244117. doi: 10.1063/1.4938422

(52) Franco-Perez, M.; Gazquez, J. L.; Ayers, P. W.; Vela, A. J. Chem.Phys. 2015, 143 (15), 154103. doi: 10.1063/1.4932539

(53) Miranda-Quintana, R. A.; Ayers, P. W. J. Chem. Phys. 2016, 144(24), 244112. doi: 10.1063/1.4953557

(54) Bochicchio, R. C.; Miranda-Quintana, R. A.; Rial, D. J. Chem. Phys.2013, 139 (19), 191101. doi: 10.1063/1.4832495

(55) Franco-Perez, M.; Heidar-Zadeh, F.; Ayers, P. W.; Gazquez, J. L.;Vela, A. Phys. Chem. Chem. Phys. 2017, 19 (18), 11588.doi: 10.1039/c7cp00224f

(56) Gyftopoulos, E. P.; Hatsopoulos, G. N. Proc. Natl. Acad. Sci. USA 1965, 60, 786.

(57) Ayers, P. W.; Yang, W. Density Functional Theory. In Computational Medicinal Chemistry for Drug Discovery; Bultinck,P., de Winter, H., Langenaeker, W., Tollenaere, J. P. Eds.; Dekker:New York, NY, USA, 2003; pp. 571–616.

(58) Ayers, P. W.; Levy, M. Theor. Chem. Acc. 2000, 103, 353.doi: 10.1007/s002149900093

(59) Valone, S. M. J. Chem. Phys. 1980, 73, 4653. doi: 10.1063/1.440656