基于最大速度扩展格子气模型的单向行人流研究
2018-07-03费经泰
费经泰,陈 喆
(安庆师范大学数学与计算科学学院,安徽安庆246133)
行人流问题的研究最早起源于交通流,近些年在研究行人流问题过程中,许多微观仿真模型被提出来,如社会力模型、元胞自动机模型、格子气模型等。其中格子气模型凭借模型简单、容易编程、适于大规模计算等优点,成为研究行人流问题的重要模型。1999年Nagatani研究小组首先将格子气模型引入到行人流模拟中,接着他们建立了一个二维偏斜随机行走格子气模型来仿真开放边界下地铁隧道内交汇人流的运动,结果表明当行人密度超过临界值以后将会发生阻塞相变,随后又研究了在周期边界条件下正方形网格上行人交通中的相变现象,并进一步讨论了开放边界条件下行人流在十字路口发生的阻塞相变[1]。2004年Kirchner首先引入多速扩展元胞自动机模型并发现最大速度vmax=3时与实测行人流基本图相吻合[2]。姜锐等提出了在随机顺序更新下最大速度扩展格子气模型,即在一个离散时间步内行人能走多个格子[3]。郝庆一等把元胞自动机中并行更新规则引入到格子气模型,发现不同于随机顺序更新规则的基本图[4]。本文在扩展格子气模型[3]的基础上,提出并行更新的最大速度扩展格子气模型。
1 模型描述
格子气模型把行人移动的宽W,长L的矩形通道划分为W×L个网格,记每个网格长度为单位1,每个格点只允许一个人占据,行人根据一定的概率选择向紧邻的左侧、前方、右侧的格点移动,但不允许后退。通道上下边界为墙壁,行人不能穿越墙壁,左右采用周期性边界条件,行人到达右边界后,从左边界处重新进入。为了分析方便,设定通道长度方向为X轴方向,通道宽度方向为Y轴方向[5],这样每个行人的位置都可以用二维坐标(x,y)来表示。图1给出了行人在格子上遇到的所有可能情形。其中叉号表示相应的位置被行人占据或上下边界,其中Pt,y,Pt,-y,Pt,x分别表示目标行人到最近左边邻居、右边邻居、前面邻居位子的转移概率,这里不考虑行人后退情况。对于行人在格子上所处的情形,相应的转移概率分别如下,

其中参数D表示偏向前的移动趋势强度。当D=0时,对应的就是不带后退的偏随机行走模型,当D=1时,前方若为空,行人只向前移动,不会考虑向两侧移动。
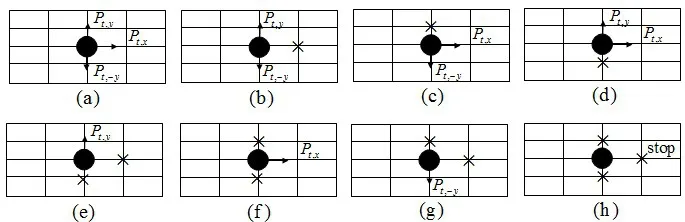
图1 行人在格子上遇到的所有可能情形
文献[3]中提出的最大速度扩展格子气模型采用了随机顺序更新的规则,为了更好地符合行人移动实际情形,本文采用并行更新方式来研究最大速度扩展格子气模型。
初始时刻N个行人随机分布在通道内,密度ρ=N/(WL),这里流率定义为每个时间步内通过右边界处的平均人数再除以宽度W。从时间步t到t+1,记每个行人n∈{1,2,…,N}的最大速度为s=vmax(n),即行人在这个时间步内最多能走s个格子,同时把行人的行走过程划分为s步来完成,则第i(i=1,2,…,s)步内更新规则如下:
(1)当i=1时,记每个行人n的位置为,并按照图1所示的8种情形计算向前方、右方、左方格点转移的概率,记更新后行人的位置为其中对于行人位置的冲突:当两个或三个行人在某一时刻试图移到同一空位时,按概率随
机选择其中一人移动到那个目标空位,其余人保持不动[4]。
(2)当i=2,3,…,s时,每个行人n的位置为关系:
(i)若,则表示行人在第i-1步内没有移动(周围没有可移动的格点或行人之间冲突导致),则这个行人就在这个时间步t内停止更新,这样做是避免出现行人在一个时间步内出现“又走又停”的现象[3]。
(ii)若,则表示行人在第i-1步内成功移动到前方格点,此时行人仍按照图1所示的8种情形来计算移动概率。
(iv)若,则表示行人在第i-1步内成功移动到左方格点,此时情形讨论同(iii)(只需将情形(iii)中的右方格点改为左方格点,并交换Pt,y和Pt,-y值)。
根据上述4种情况计算行人转移概率,并记更新后的位置为Ti(+n)1(t)=(x(in+)1(t),yi(+n)1(t))。其中行人位置的冲突处理同i=1情形。这里通过修改格子气模型的基本概率,令Pt,y=0或Pt,-y=0,则行人向左(右)方移动的概率为零,这样可以避免行人在移动过程中出现“乒乓行为”[3],即行人路径上出现重叠(如行人在向右侧行走后在下一步又向左侧行走)。当更新完s步后,该时间步t结束,进入下一个时间步t+1更新。
2 模拟结果及讨论
仿真参数选取模型尺寸大小W×L=100×100,模拟的总时间T=15000,其中取后5 000个时间步长用来统计数据和计算流率。
2.1 参数D对基本图的影响
图2表示D<1基本图,从图2(a)和图2(b)中可以看出扩展后模型的流率高于vmax=1的流率。随着D的增大,扩展格子气模型保持了文献[4]中提到的并行格子气模型的特点:密度—流率曲线在临界密度处出现了拐点,它的右分支(拥挤分支)变成了下凸曲线。其中在图2(c)和图2(d)中,随着D(D>0.5)的增大,当密度ρ大于临界密度后,流率会出现突降,说明行人从自由流状态向拥挤流状态的转变过程中发生了相变。由于扩展格子气模型vmax>1,从而在一个时间步内,行人之间相互作用范围扩大,不仅限于前左右的邻居。根据模型的规则,行人在一个时间步内能走vmax个格子,从而很容易造成堵塞,流率突降。

图2 不同参数D基本图
图3 表示参数D=1的基本图,基本图由两条分支组成,上分支由初始分布为均匀状态模拟得到,下分支是由初始分布为随机状态模拟得到的[4]。通过观察基本图可以发现,vmax>1格子气模型与vmax=1的格子气模型有很大的不同,当vmax=1时,流率曲线出现了两个拥挤分支,而vmax>1的格子气模型呈现出交通流基本图中典型的反λ形状,原因是最大速度扩展格子气模型在模拟过程中不能维持初始均匀分布状态[4]。同时从图中可以看出,在临界密度附近形成亚稳态区域(0.3±0.05≤ρ≤0.5±0.05),在这个密度范围内,行人的流率和分布状态是不稳定的,这也解释了图2中基本图出现流率突降现象的原因。
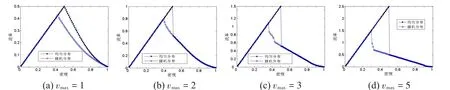
图3 参数D=1基本图
2.2 最大速度vmax对基本图的影响
图4 (c)显示了在参数vmax=3下,密度—流率曲线的临界密度ρ≈0.35,符合文献[3]中提到的实测行人流的临界密度ρ≈0.34。从图4中可以看出,随着vmax的增大,最大流率对应的临界密度不断减小。在图4(a)和图4(b)中,流率随vmax的增大而增大。图4(c)和图4(d)出现了行人流中“快即是慢”的现象,如图4(d),当密度0.35≤ρ≤0.55时,最大速度vmax=5时的流率反而小于vmax=2,3时的流率,而在其他的密度区域上恰好相反。原因是这一段密度区域是上面提到的亚稳态区域,行人流率不稳定。当密度ρ≤0.35时,行人处于自由流的状态,最大速度越大,流率越大,当密度ρ≥0.55时,行人分布从亚稳态转变成高密度拥挤状态,此时速度对流率的大小又起着较大的影响,所以最大速度越大,流率也越大。
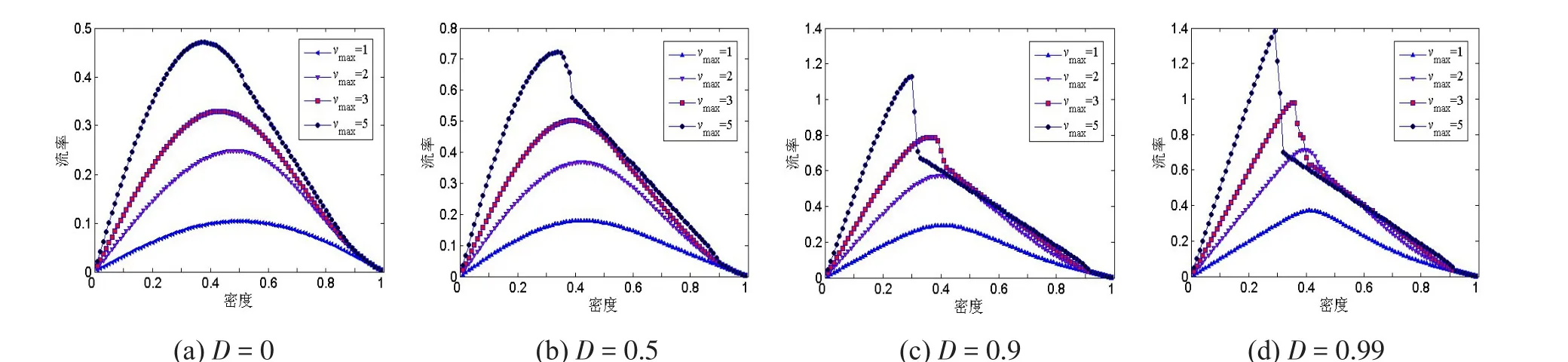
图4 不同参数vmax基本图
3 总结
本文在原有的最大速度扩展格子气模型的基础上采用并行更新的方式,通过仿真模拟得到了行人流基本图,并得到以下结论:扩展后vmax>1格子气模型在流率上有很大的提高,最大流率所对应的临界密度小于原模型,从而更接近实际情况。基本图中流率曲线在从自由流分支向拥挤流分支转变过程中发生了相变,流率突降,同时出现了行人流中“快即是慢”的现象,即最大速度越大,反而流率越小。当参数D=1,行人流基本图呈现出和车辆交通流基本图类似的典型的反λ形状。在今后工作中,将进一步改进模型,如将模型与博弈论、行人移动路径的选择等问题相结合,以更好地模拟实际行人流。
[1]MURAMATSU M,NAGATANI T.Jamming transition of pedestrian traffic at a crossing with open boundaries[J].Physica A,2000,286(1-2):377-390.
[2]KIRCHNER A,KLÜPFEL H,NISHINARI K,et al.Discretization effects and the influence of walking speed in cellular automata models for pedestrian dynamics[J].Journal of Statistical Mechanics:Theory and Experiment,2004,2004(10):P10011.
[3]JIANG R,WU Q S.Pedestrian behaviors in a lattice gas model with large maximum velocity[J].Physica A:Statistical Mechanics and its Applications,2007,373(36):683-693.
[4]HAO Q Y,HU M B,CHENG X Q,et al.Pedestrian flow in a lattice gas model with parallel update[J].Phys Rev E,2010,82(2):026133.
[5]李明华,袁振洲,许琰,等.基于改进格子气模型的对向行人流分层现象的随机性研究[J].物理学报,2015,64(1):427-438.
[6]马佩杰.行人流综述[J].上海理工大学学报,2012,34(2):185-203.
[7]YUAN W F,TAN K H.A novel algorithm of simulating multivelocity evacuation based on cellular automata modeling and tenability condition[J]. Physica A:Statistical Mechanics and its Applications,2007,379(1):250-262.
