一种面向弹道再入目标跟踪的HPD-SRCQSPF算法
2018-07-03郑丽涛
杨 峰,郑丽涛
(1. 西北工业大学自动化学院,西安 710129;2. 信息融合技术教育部重点实验室,西安 710129)
0 引 言
非线性滤波广泛应用在生活中的各个领域,常见的非线性滤波器有EKF、UKF[1]和最近几年提出的CQKF[2]。其中,CQKF[2]算法是CKF[3]算法的一般化形式。这三种滤波算法在工程中都得到了广泛应用,然而针对不同的非线性系统,三种滤波算法有着各自的优势和缺陷。通常,EKF算法的滤波精度为一阶;UKF算法的滤波精度为二阶;CQKF算法的滤波精度为三阶[2,4]。另外,当系统阶次不同时,这三种滤波算法的滤波精度也存在差异。当系统阶次大于3时,CQKF算法的滤波估计效果是最好的[2,4]。因此,对于弹道再入目标轨迹跟踪模型,CQKF显然有着明显的优势。但CQKF算法在迭代中,由于协方差矩阵的舍入误差累积,会导致协方差矩阵渐渐失去正定性,甚至会造成滤波发散。文献[5]提出了平方根容积求积卡尔曼滤波(SRCQKF)算法,其在时间和量测的更新过程中不需要直接计算协方差矩阵,而是通过协方差矩阵的平方根形式来代替,这避免了协方差矩阵非正定时导致滤波发散的问题,从而对弹道再入目标轨迹跟踪模型有着更好的估计效果。
在实际生活中,弹道目标跟踪问题是一个强非线性和非高斯问题[6],其在巡航飞行[7]、月球探测[8]和火星探测[9]等多个领域有着广泛的应用。因此,本文中,过程噪声为非高斯环境下的闪烁噪声。文献[10]提出,在闪烁噪声条件下,SPF的估计效果要优于EKF、UKF等次优卡尔曼滤波。因此,SPF对于闪烁噪声条件下的弹道再入目标轨迹跟踪模型有着很好的跟踪效果。SPF[11]算法是一种基于贝叶斯估计理论的序贯蒙特卡洛模拟方法,然而在粒子滤波中不可避免地存在着粒子退化[12]问题。针对该问题,可以选择滤波估计后的值作为粒子滤波算法采样的重要性密度函数。文献[13]选择SRCQKF估计后的值作为粒子滤波算法中的重要性密度函数,即平方根容积求积粒子滤波(SRCQPF)算法。
SRCQPF算法虽然解决了粒子滤波的退化问题,但也同样带来了运算量大,运算时间过长等问题[13-14]。基于文献[15]提出的混合建议分布的框架,本文提出了平方根容积求积采样粒子滤波(HPD-SRCQSPF)算法,该算法是将平方根容积求积卡尔曼滤波估计后的值作为多模型采样粒子滤波的一个基本建议分布。由于HPD-SRCQSPF算法是采用了多个建议分布,该算法的运算时间会略长于SPF算法,但其滤波精度却远远高于SPF算法和SRCQPF算法;特别是在弹道再入目标轨迹跟踪问题中,本文算法可以取得很好的跟踪效果。
1 标准粒子滤波(SPF)
粒子滤波的基本思想是依据系统状态向量的经验分布[14],在状态空间中产生一组被称为粒子的随机离散样本集合。然后根据最新的量测用似然函数来调整粒子所占的权值,从而对最初的经验分布进行修正。
考虑如下动态系统,即状态空间模型。其中状态方程和量测方程分别为:
xk=f(xk-1,wk-1)
(1)
zk=h(xk,vk)
(2)
式中:xk∈Rnx为k时刻的系统状态向量,zk∈Rny为k时刻的量测向量,wk-1∈Rnw和vk∈Rnv分别表示过程噪声和量测噪声。f:Rnx×Rnw→Rnx为状态转移函数,h:Rnz×Rnv→Rnz为量测函数。
假设已知状态的初始概率密度函数为p(x0|y0),且x0,x1,…,xk服从于一阶马尔科夫过程,状态序列为Xk={x0,x1,…,xk},观测序列为Zk={z0,z1,…,zk}。在贝叶斯框架下,滤波分布p(xk|zk)的递推通过预测与更新两步完成。
预测:
(3)
式中:p(zk|xk-1)为状态方程的一步预测转移密度,而p(xk-1|zk-1)为前一时刻的后验密度。
更新:
(4)
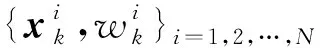
(5)
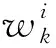
(6)
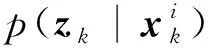
针对粒子退化的情况,可以根据退化程度加入重采样步骤。
2 平方根容积求积粒子滤波(SRCQPF)
2.1 平方根容积求积卡尔曼滤波(SRCQKF)
传统的CKF算法是将多维高斯积分转换成径向积分和球面积分的形式,CQKF算法在求取径向积分时是通过高斯—拉盖尔积分准则去逼近积分运算。因此,CQKF是CKF滤波算法的一般化形式。
在实际应用中,CQKF算法在递推过程中协方差矩阵P由于舍入误差累积的原因会导致其逐渐的失去正定性,最终导致滤波算法发散。平方根容积求积卡尔曼滤波(SRCQKF)在时间和量测的更新过程中通过求解协方差矩阵的平方根形式来代替协方差矩阵,这避免了协方差矩阵非负定时导致滤波发散的问题。因此,相比于CQKF算法,SRCQKF算法有着更好的工程实际应用效果。
2.2 SRCQPF算法
标准粒子滤波算法虽然在处理非高斯问题中有着明显的优势,但该算法不可避免的一个问题就是粒子退化问题,而选择适合的重要密度函数可以有效改善该问题。SRCQPF算法[13]就是把SRCQKF算法和SPF算法结合起来,将SRCQKF滤波后的值作为SPF算法的重要性密度函数,这可以提高粒子的滤波精度,使得采样后的粒子向似然比高的区域移动,从而减轻粒子退化问题。
SRCQPF算法的具体步骤如下:
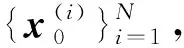
2)用SRCQKF对每一粒子进行状态更新。
3)计算粒子点对应的权值
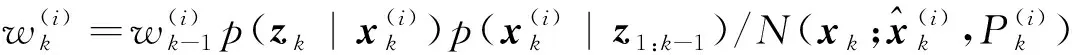
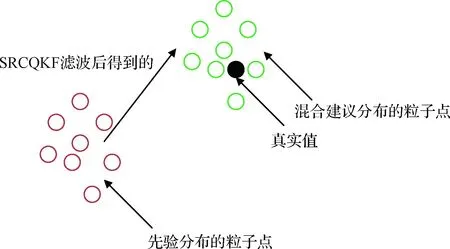
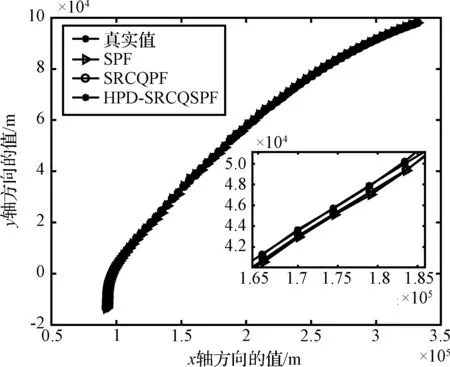
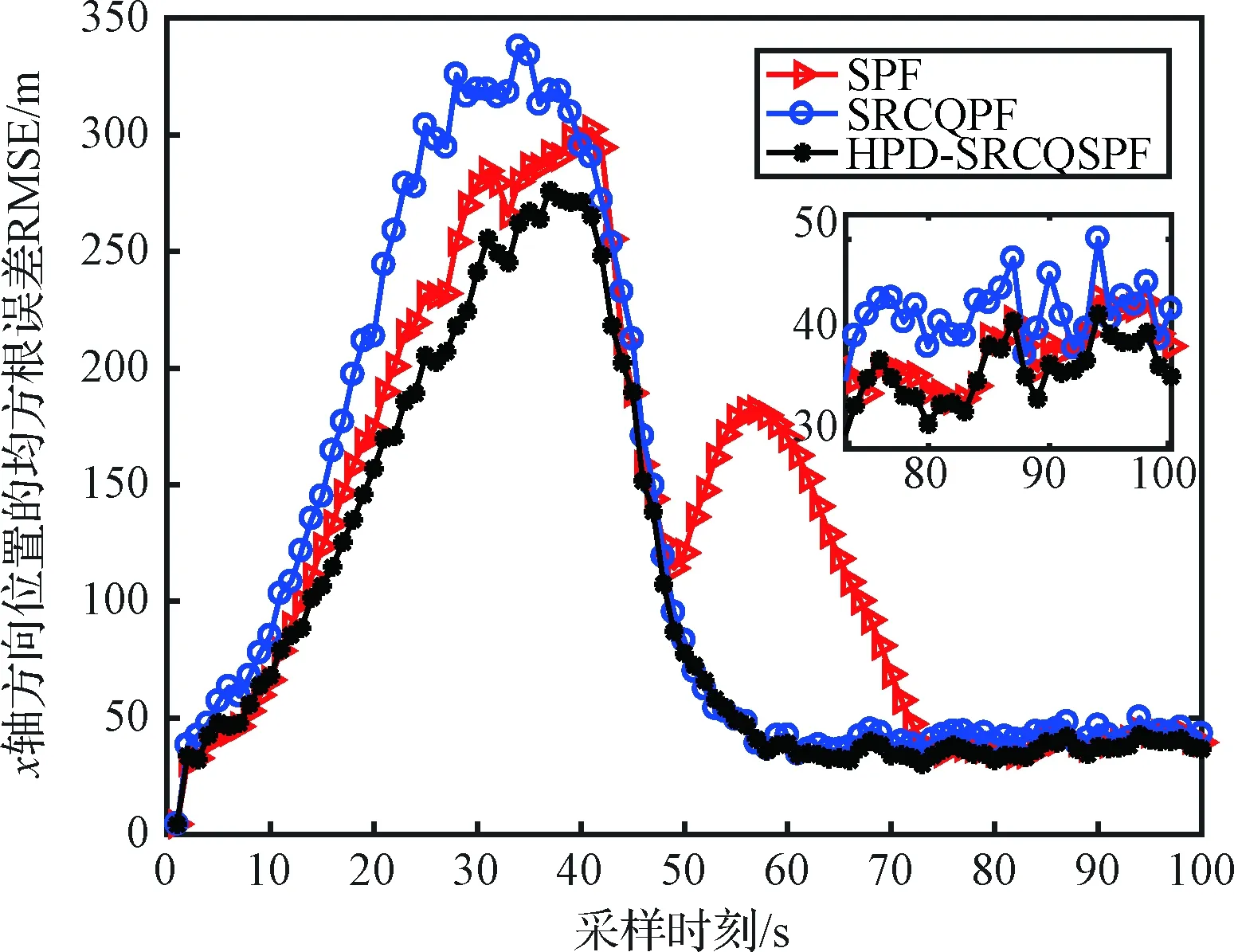
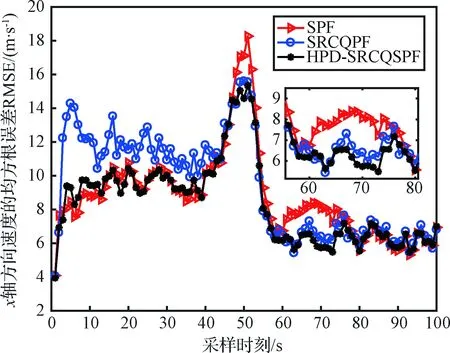
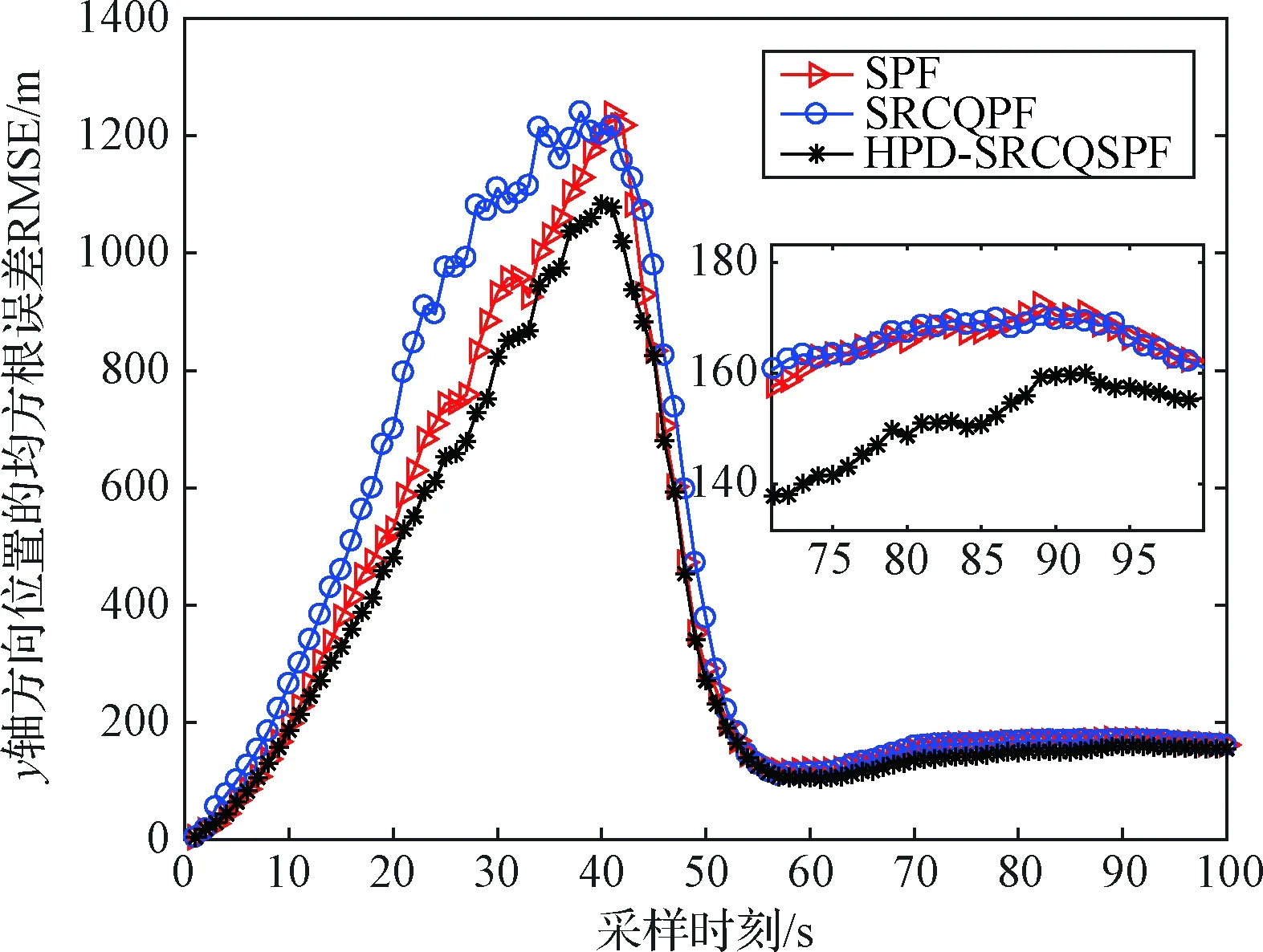
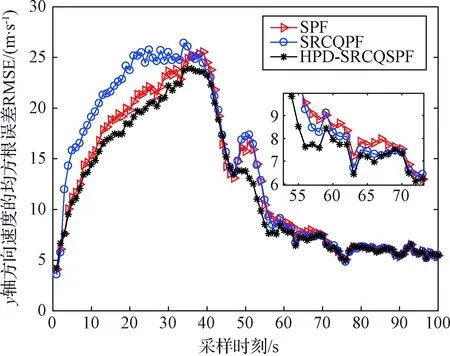
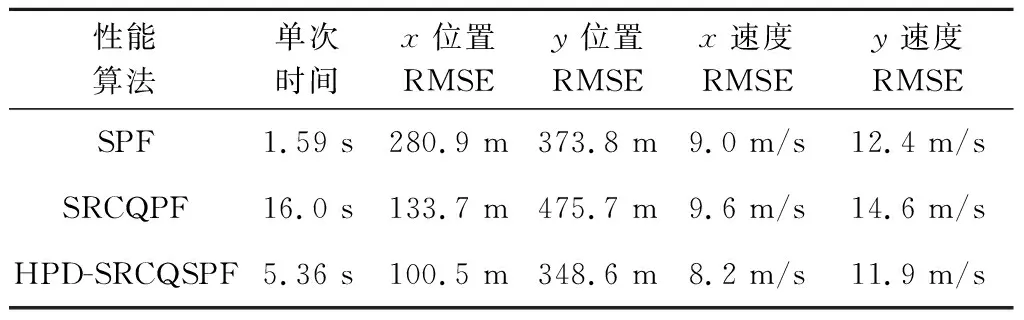
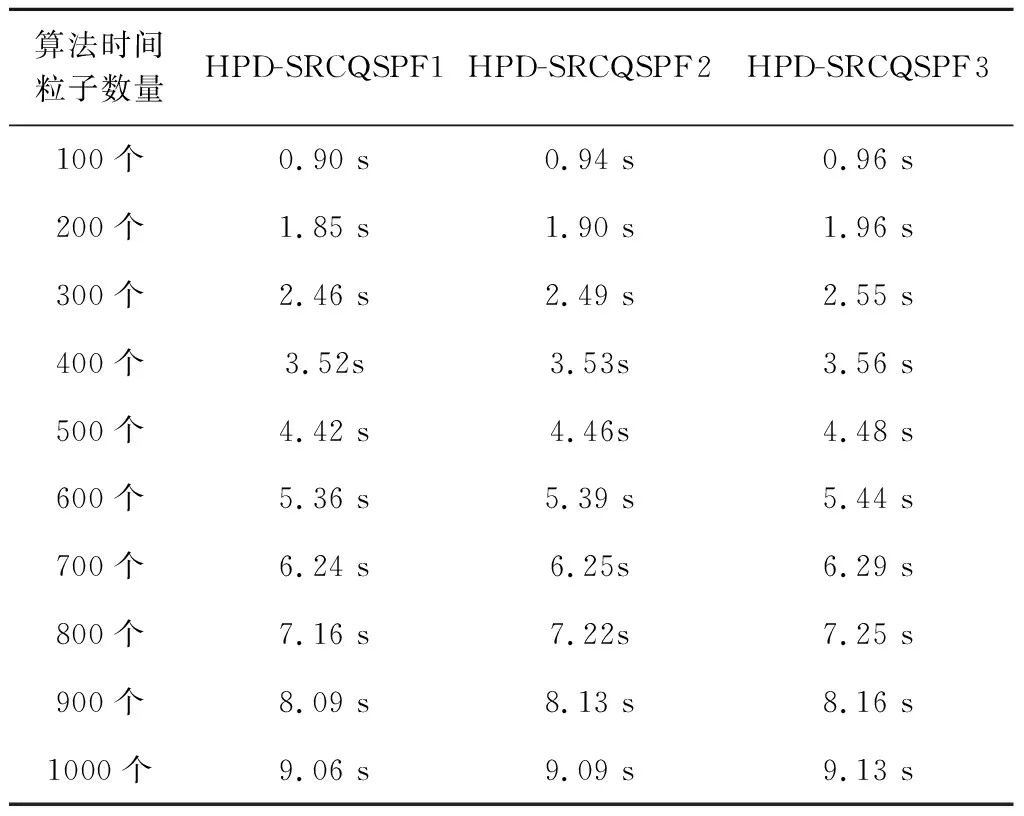
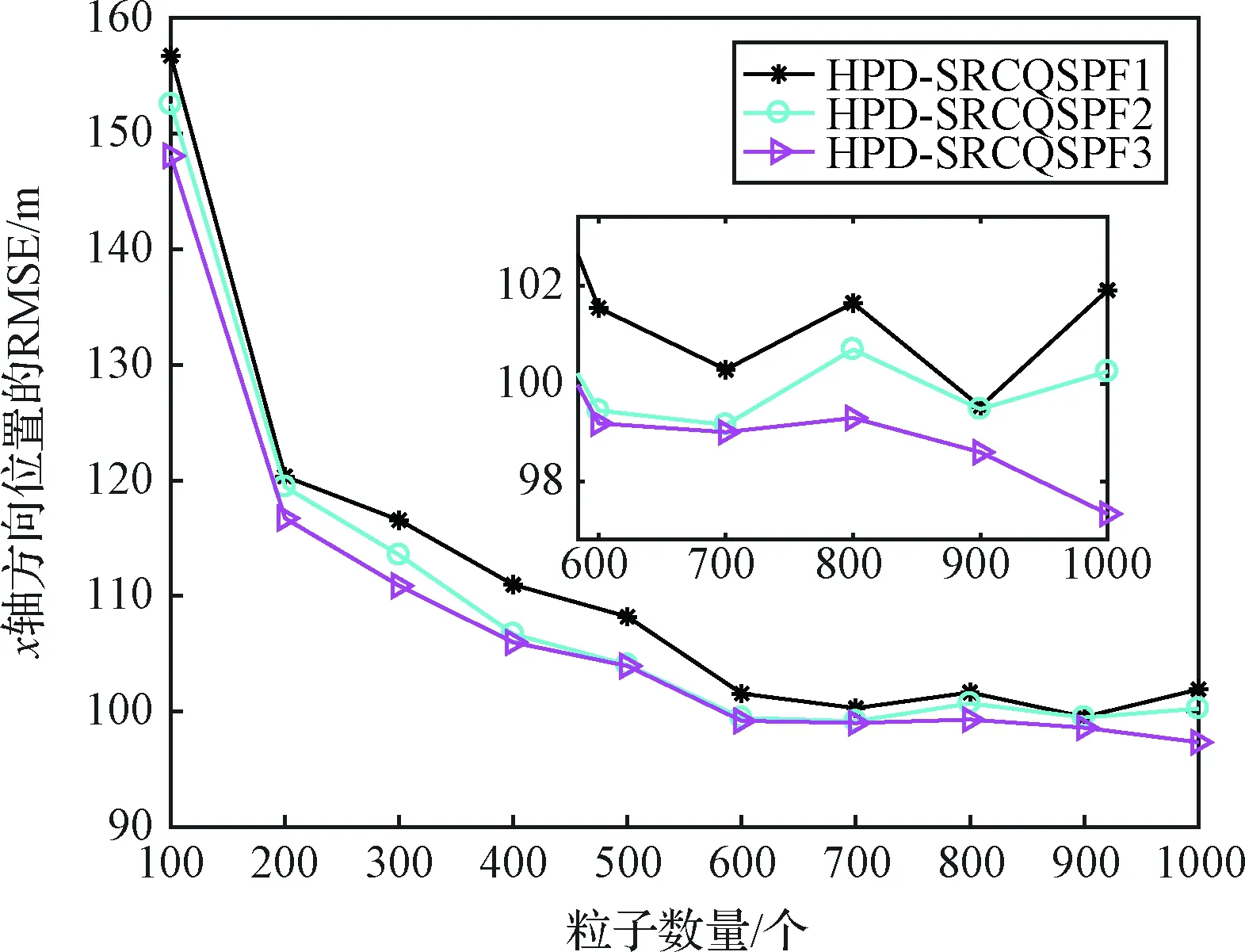
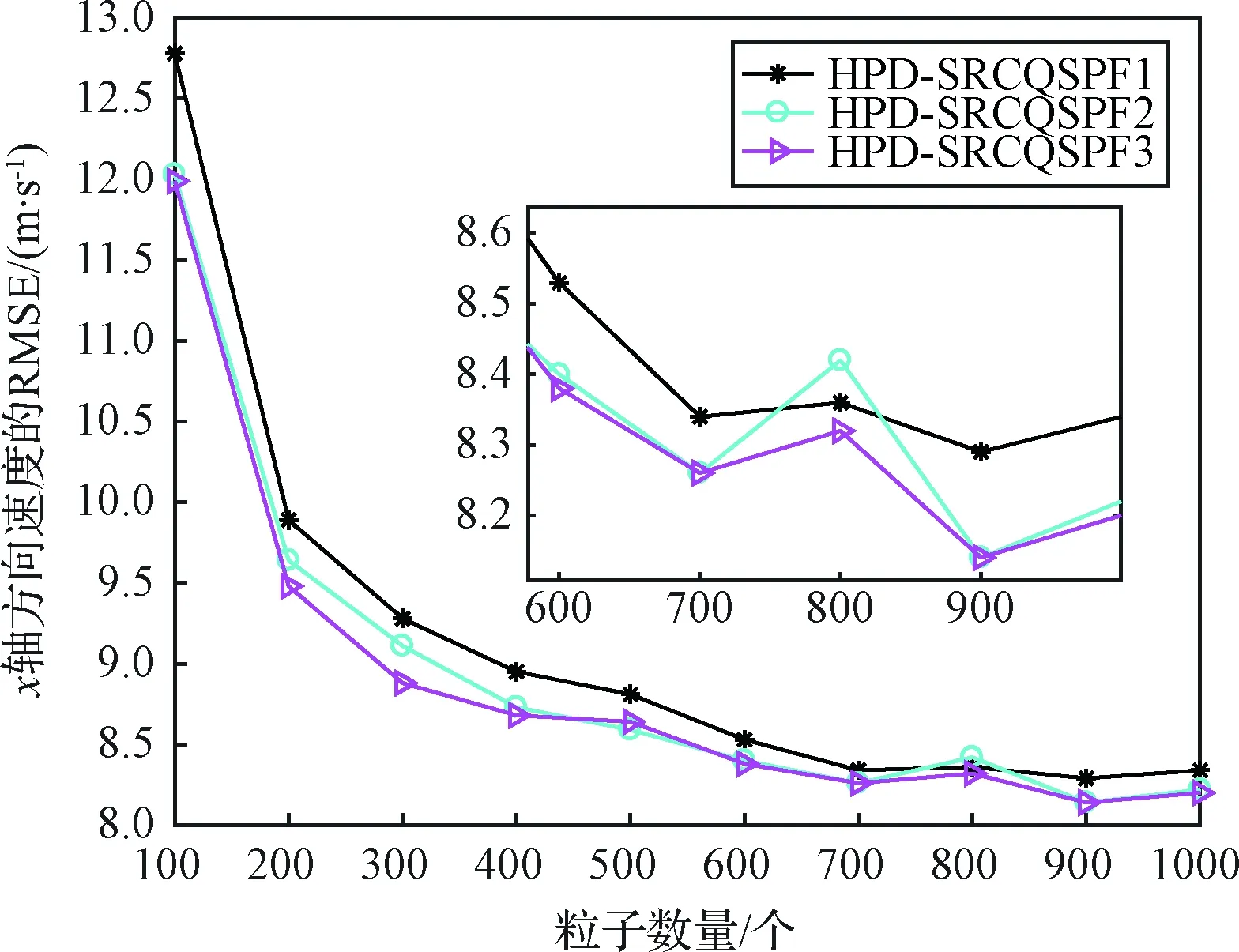
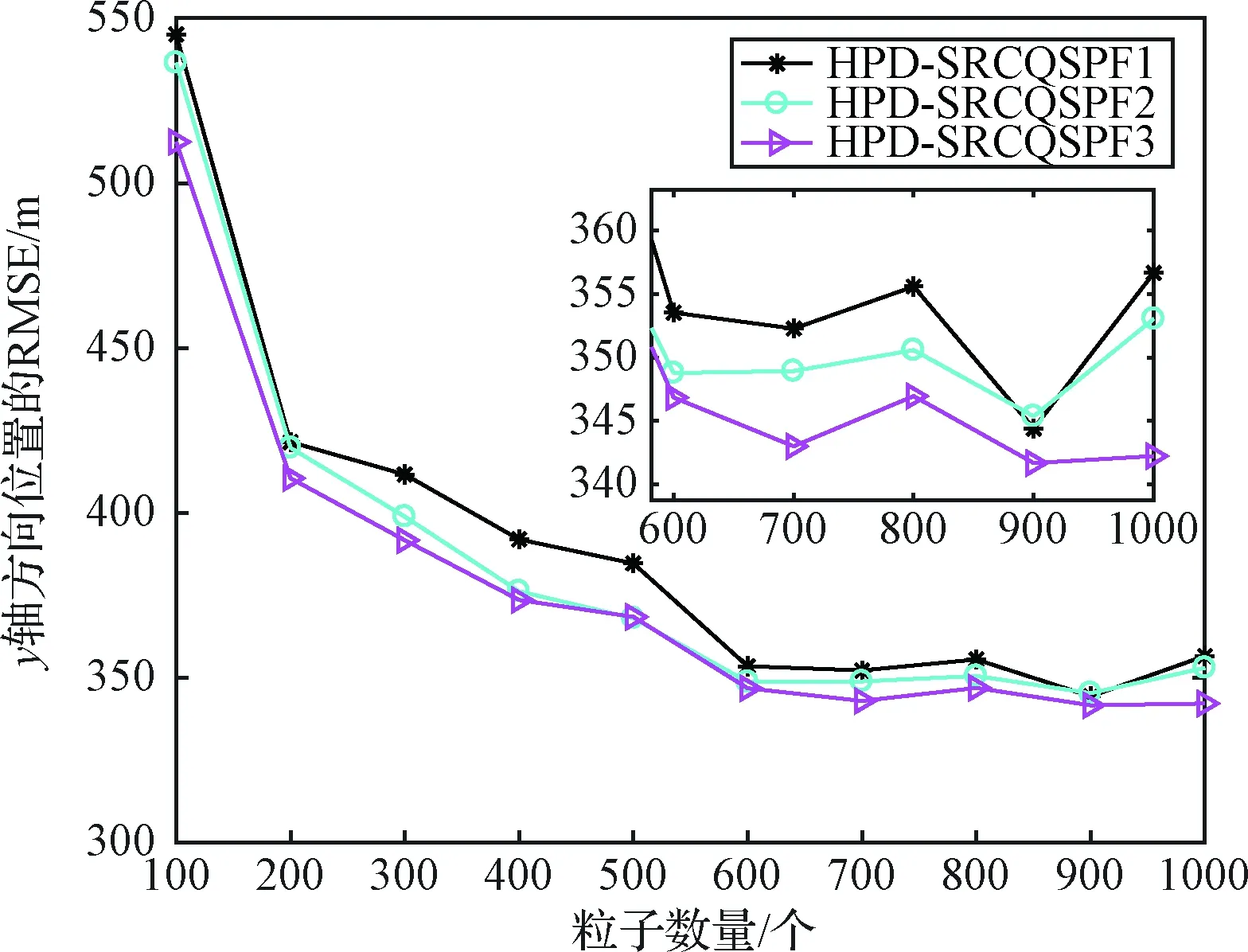
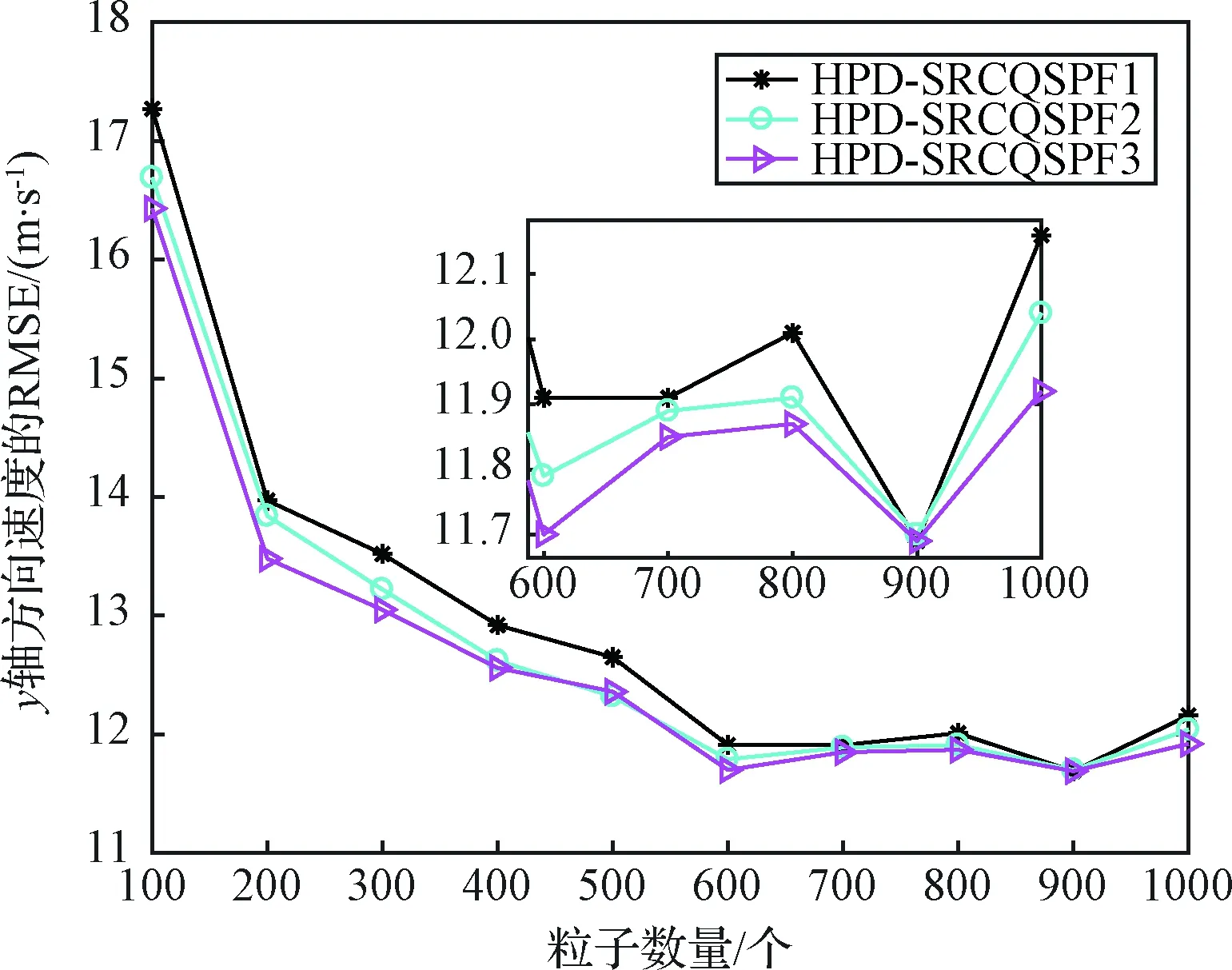
4)Neff 5)将k时刻的粒子点作为k+1时刻的初始粒子点。 文献[15]提出了混合建议分布的概念,其核心是对建议分布进行创新,即用几种基本建议分布的加权来代替原来单一的建议分布。 (7) 关于基本建议分布,有下式: (8) 所以混合建议分布可以表示为: (9) (10) 式(10)中,等式右面第一项反映了量测信息的重要性,其中p(yt|zt)=pw(zt-yt)=p(zt|yt)。等式右面第二项反映的是预测信息的重要性。 为了计算的可行性,可以将式(10)转化为式(11)所示的矩阵形式。 (11) 式中: (12) (13) (14) (15) 其中, (16) (17) (18) 则 确定了Δjl和Δj的值后,求解式(10)的最小值问题就显得很容易了。 在本文中,令m=2,即混合建议分布由两个基本的建议分布组成。 那么,混合建议分布可表示为 式(10)的最小值问题可以简化为 (19) 为了直观地表示HPD-SRCQSPF算法,现将混合建议分布的示意图表示如图1。 图1 混合建议分布示意图Fig.1 The picture of hybrid proposal distribution 可以看出,在图1的情况下,只利用先验分布得到的粒子点会远离真实值。而通过混合建议分布后,粒子点可以分布在真实值附近,从而使滤波估计值更加准确。 HPD-SRCQSPF算法的具体步骤如下: 3)计算出Δ11,Δ12,Δ22,Δ1,Δ2。 6)计算粒子点对应的权值 7)Neff 8)将k时刻的粒子点作为k+1时刻的初始粒子点。 9)重复步骤2)~8) 最后得到k时刻状态量的估计为 文献[6]和文献[10]已经对弹道再入目标的数学模型进行了较为系统的分析。根据文献[16],假定地球表面为平面,目标为质点且不考虑自旋。 则弹道再入目标数学模型的运动方程和观测方程可表示为式(20)和式(21)。 xk+1=f(xk,β)+wk (20) zk+1=h(xk+1)+vk+1 (21) p(vk+1)= 0.5p1(vk+1)+0.5p2(vk+1)= 0.5N(vk+1;0,R1)+0.5N(vk+1;0,R2) 其中, (22) (23) 状态方程中的f(xk,β)可表示为式(24) (24) 式(24)中,等式右面的后两项表示空气阻力和重力对目标状态变量的影响作用。g是重力加速度,m(xk,β)是空气动力阻力函数,β是弹道系数,为了简化模型,根据文献[10],可以将弹道系数定为确定参数,即β=40000 kg/ms2。 (25) 空气动力阻力函数m(xk,β)定义为: (26) ρ(·)是随着海拔高度呈指数衰落的空气密度函数,可以定义ρ(yk)=c1e-c2yp,k-1,当yp,k-1<9144时,c1=1.227,c2=1.093×10-4;当yp,k-1>9144时,c1=1.754,c2=1.49×10-4。因此,在yp,k-1=9144时,目标会有明显的机动运动。 量测方程h(·)可表示为 (27) 仿真中,仿真时间为200 s,蒙特卡洛次数为500次,粒子数为600。目标的初始状态为 其余的仿真参数设置如表1所示。 表1 仿真参数设置Table 1 The simulation parameters 分别用SPF[11]算法、SRCQPF[13]算法和本文提出的HPD-SRCQSPF算法对上述的弹道再入目标数学模型进行仿真,仿真结果如图2所示。 图2 单次跟踪效果Fig.2 Single tracking effect 从图2可以看出,在单次跟踪中,比起SPF和SRCQPF算法,HPD-SRCQSPF算法明显更接近于真实值,且在图2中小图标记出的位置尤为明显。这是因为本文算法的建议分布采用了多个基本建议分布加权的形式,所以可以更好地逼近后验分布,因此有着很好的估计效果。 图3 x轴方向位置的RMSEFig.3 RMSE in the position of x direction 图4 x轴方向速度的RMSEFig.4 RMSE in the velocity of x direction 图5 y轴方向位置的RMSEFig.5 RMSE in the position of y direction 图6 y轴方向速度的RMSEFig.6 RMSE in the velocity of y direction 从图3~6可以看出,45 s左右各个算法对目标的跟踪精度都有较大的波动,这是因为空气密度函数ρ(·)的值在此刻发生了变化,从而导致目标在此时发生了强机动性运动。 前45 s,HPD-SRCQSPF算法对目标的跟踪效果略好于SPF算法,且它们的跟踪效果都好于SRCQPF算法。这是因为此时目标的运动较平稳,本文算法的建议分布中先验分布占了很大的权重,所以本文算法和SPF算法都有着较好的估计效果。 50 s之后,HPD-SRCQSPF算法明显好于SPF和SRCQPF算法,且收敛速度和最终的滤波精度都略优于另外两种算法。这是因为本文算法用了混合建议分布的框架,可以动态地选择每个基本建议分布所占的权重,所以其比起另外两种算法会有着较好的估计效果。 SPF,SRCQPF和HPD-SRCQSPF算法对该数学模型进行仿真的各项算法性能如表2所示。 表2 各个算法的性能Table 2 The performance of each algorithm 从表2可以看出,HPD-SRCQSPF算法的运算时间虽然高于SPF算法,但却远远低于SRCQPF算法。这是因为比起SPF算法,本文算法需要计算SRCQKF的估计值,因此其时间会略长于SPF算法。本文算法在x轴位置、速度以及y轴位置、速度方面的RMSE都远远低于另外两种算法,这证明了基于先验分布的基本建议分布和基于SRCQKF估计后值的基本建议分布的加权和形式的混合建议分布对弹道再入目标数学模型的跟踪是很有效的。 在HPD-SRCQSPF算法中,选择SRCQKF估计后的值作为粒子滤波算法中的重要性密度函数。当SRCQKF算法的切比雪夫多项式是采用一阶近似计算时,HPD-SRCQKF算法即为HPD-SRCSPF算法,在本文中,将其记为HPD-SRCQSPF 1。当SRCQKF算法的切比雪夫多项式是采用二阶近似时,将其记为HPD-SRCQSPF 2。当SRCQKF算法的切比雪夫多项式是采用三阶近似时,将其记为HPD-SRCQSPF 3。 为了分析本文算法不同阶数以及不同粒子数对最终估计精度的影响,用HPD-SRCQSPF 1,HPD-SRCQSPF 2和HPD-SRCQSPF 3三种算法分别在粒子数为100,200,300,400,500,600,700,800,900和1000的情况下对上述的弹道再入目标数学模型进行仿真,仿真结果如下。 表3 不同阶数和不同粒子数的仿真时间Table 3 The simulation time of different orders and different particles 从表3可以看出,在单次的仿真试验中,随着粒子数的增多,仿真时间逐渐增多,每多100个粒子点大约会增加1 s。随着切比雪夫阶数的增加,会导致采样点的数量增加,从而导致仿真时间也是不断增加的。但由于不同阶数HPD-SRCQSPF算法的采样点及其权重是可以脱机运算的,因此切比雪夫阶数每增加一阶只会增加0.02 s的运算时间。 从图7~10可以看出,随着粒子点数量的增加,在各个方向上的估计精度是不断提高的。但可以看出,在粒子数目大于600个粒子点后,估计精度的增加小到几乎可以忽略不计,因此最优的粒子点数目是600个。在HPD-SRCQSPF算法中,随着切比雪夫阶数的提高,估计精度也是逐渐提升的。这是因为高的切比雪夫阶数可以更好地逼近后验分布,因此会使得滤波的估计效果更好。 图7 不同阶数和不同粒子数在x轴方向位置的RMSEFig.7 The RMSE in the x position of different orders and different particles 图8 不同阶数和不同粒子数在x轴方向速度的RMSEFig.8 The RMSE in the x velocity of different orders and different particles 图9 不同阶数和不同粒子数在y轴方向位置的RMSEFig.9 The RMSE in the y position of different orders and different particles 图10 不同阶数和不同粒子数在y轴方向速度的RMSEFig.10 The RMSE in the y velocity of different orders and different particles 综上可知,在弹道再入目标轨迹跟踪的数学模型中,综合切比雪夫阶数和粒子数,最优的选取策略应该是HPD-SRCQSPF 3算法在选取600个粒子点的情况下。 在弹道再入目标轨迹跟踪模型中,相比于SPF算法和SRCQPF算法,本文所提的HPD-SRCQSPF算法不仅有着较低的运算量,而且有着很好的跟踪效果。特别是对于该模型中机动的情况,本文的算法可以在较短的时间内获得很高的估计精度。另外,在该模型中,综合切比雪夫阶数和粒子数,在HPD-SRCQSPF算法中,最优的选取策略应该是三阶切比雪夫HPD-SRCQSPF 3算法在选取600个粒子点的情况下。 参 考 文 献 [1] Julier S, Uhlmann J, Durrant-Whyte H F. A new method for the nonlinear transformation of means and covariances in filters and estimators [J]. IEEE Transactions on Automatic Control, 2001, 45(3): 477-482. [2] Bhaumik S. Cubature quadrature Kalman filter [J]. IET Signal Processing, 2013, 7(7): 533-541. [3] 孙枫,唐李军.Cubature 卡尔曼滤波-卡尔曼滤波算法[J].控制与决策,2012, 27(10): 1561-1565. [Sun Feng, Tang Li-jun. Cubature Kalman filter-Kalman filter algorithm [J]. Control and Decision, 2012, 27(10): 1561-1565.] [4] 王小旭, 潘泉, 黄鹤,等. 非线性系统确定采样型滤波算法综述 [J]. 控制与决策, 2012, 27(6): 801-812. [Wang Xiao-xu, Pan Quan, Huang He, et al. Overview of deterministic sampling filtering algorithms for nonlinear system [J]. Control and Decision, 2012, 27(6): 801-812.] [5] Bhaumik S. Square-root cubature-quadrature Kalman filter [J]. Asian Journal of Control, 2014, 16(2): 617-622. [6] 刘也, 余安喜, 朱炬波, 等. 弹道目标实时跟踪中的滤波方法综述[J]. 宇航学报, 2013, 34(11): 1417-1426. [Liu Ye, Yu An-xi, Zhu ju-bo, et al. Survey of filter algorithms for ballistic target real-time tracking [J]. Journal of Astronautics, 2013, 34(11): 1417-1426.] [7] 郭行, 符文星, 付斌, 等. 吸气式高超声速飞行器巡航段突防弹道规划[J]. 宇航学报, 2017, 38(3): 287-295. [Guo Hang, Fu Wen-xing, Fu Bin, et al. Penetration trajectory programming for air-breathing hypersonic vehicles during the cruise phase [J]. Journal of Astronautics, 2017, 38(3): 287-295.] [8] 宋叶志, 黄勇, 胡小工, 等. 月球探测软着陆与采样返回段弹道确定[J]. 宇航学报, 2016, 37(10): 1157-1163. [Song Ye-zhi, Huang Yong, Hu Xiao-gong, et al. Trajectory determination for lunar probe soft landing and sampling return [J]. Journal of Astronautics, 2016, 37(10): 1157-1163.] [9] 高兴龙, 张青斌, 丰志伟,等. 集成火星进入弹道的开伞过程动力学特性研究 [J]. 宇航学报, 2016, 37(6): 664-670. [Gao Xing-long, Zhang Qing-bin, Feng Zhi-wei, et al. Study on dynamic characteristic of opening process integrating with Mars entry trajectory [J]. Journal of Astronautics, 2016, 37(6): 664-670.] [10] 田亚菲, 莫骅, 于飞. 弹道再入目标轨迹跟踪中非线性滤波算法研究 [J]. 舰船电子工程, 2014, 34(3): 39-43. [Tian Ya-fei, Mo hua, Yu fei. Nonlinear filtering algorithm on ballistic reentry target trajectory tracking [J]. Ship Electronic Engineering, 2014, 34(3): 39-43.] [11] Cappé O, Godsill S J, Moulines E. An overview of existing methods and recent advances in sequential Monte Carlo [J]. Proceedings of the IEEE, 2007, 95(5): 899-924. [12] Christoffersson J. A resampling method for regression models with serially correlated errors [J]. Computational Statistics & Data Analysis, 1997, 25(1): 43-53. [13] Kiani M, Pourtakdoust S H. Adaptive square-root cubature-quadrature Kalman particle filter for satellite attitude determination using vector observations [J]. Acta Astronautica, 2014, 105(1): 109-116. [14] 胡士强,敬忠良.粒子滤波算法综述[J].控制与决策,2005, 20(4): 361-371. [Hu Shi-qiang, Jing Zhong-liang. Overview of particle filter algorithm [J]. Control and Decision, 2005, 20(4): 361-371.] [15] Zuo J, Liang Y, Zhang Y Z, et al. Particle filter with multimode sampling strategy [J]. Signal Processing, 2013, 93(11): 3192-3201. [16] Li X R, Jilkov V P. Survey of maneuvering target tracking. Part II: motion models of ballistic and space targets [J]. IEEE Transactions on Aerospace & Electronic Systems, 2010, 46(1): 96-119.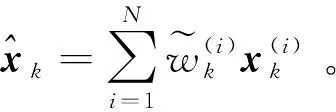
3 基于混合建议分布的平方根容积求积采样粒子滤波(HPD-SRCQSPF)
3.1 混合建议分布(HPD)
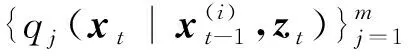
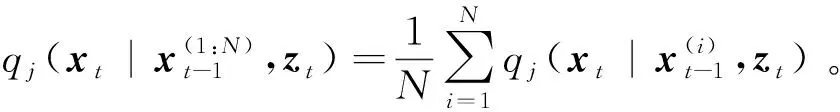
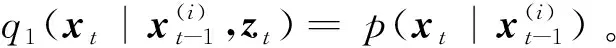
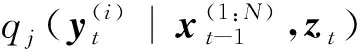
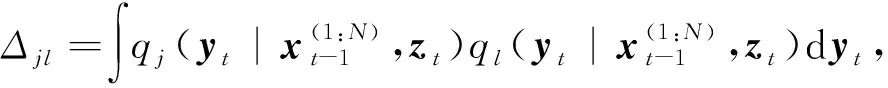
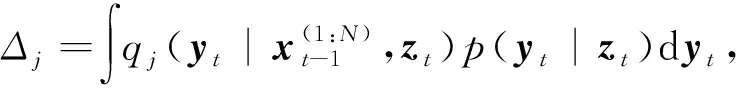
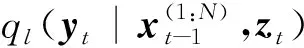
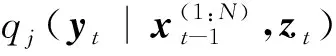
3.2 HPD-SRCQSPF算法
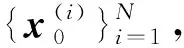
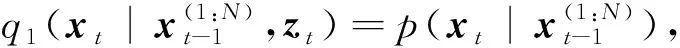
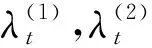
4 仿真校验
4.1 仿真场景
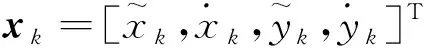

4.2 仿真分析
4.3 HPD-SRCQSPF算法的仿真分析
5 结 论
