一种三维地形特征提取和匹配方法
2018-07-03李国庆
田 阳,李国庆,2,宋 新
(1. 哈尔滨工业大学深空探测基础研究中心,哈尔滨 150080;2. 北京空间飞行器总体设计部,北京 100094;3. 哈尔滨工业大学电子与信息工程学院,哈尔滨 150080)
0 引 言
利用光学设备感知环境是航天器尤其是行星漫游器和着陆器等工作在陌生环境中的航天器必备能力之一[1]。例如NASA的Spirit,Opportunity和Curiosity火星漫游器,以及我国的玉兔月球漫游器[2]都装备了双目相机获取周围的三维地形信息,NASA最新的OSIRIS-REx小天体探测任务中,着陆器搭载了工作距离超过7 km的LiDAR敏感器,在着陆阶段测量着陆器高度和天体表面地形[3]。除了利用三维地形数据感知岩石、陨石坑和陡坡等对航天器构成危险的地形和障碍之外,三维数据还可以用来进行航天器导航定位。利用连续的三维地形数据序列能够确定漫游器或是着陆器的帧间相对运动,这与Spirit和Opportunity漫游器采用的视觉里程计类似。另一种方式是将获得的三维地形数据与导航地形数据库对比,确定航天器在导航坐标系下的位置和姿态。不过这都建立在准确匹配三维地形数据的基础上。
LiDAR或双目相机获取的三维地形数据一般是三维点云,匹配三维点云可以采用迭代最近点(Iterative Closest Point,ICP)方法[4]和该方法的多种变形[5-6]。ICP其实是一种非线性最小二乘方法,通过迭代旋转和平移参数不断缩小点云间的空间距离,在三维点云匹配中得到广泛应用,但是该方法需要猜测合适的迭代初值,效果较好的ICP变形方法将考察点到点距离改为点到平面距离,这需要对点云数据逐点计算平面法线方向,计算量较大。另一类三维点云匹配方法与二维图像特征匹配方法类似,首先在点云数据中检测形状或曲率具有显著性的点作为特征,利用特征邻域内的点云形成描述矢量(描述符),通过计算描述矢量的相似性判断特征匹配与否。
出于任务安全性的考虑,行星漫游器或着陆器工作环境都经过精心设计,如行星着陆任务的着陆点一般都选择地形平坦的区域,行星漫游器在路径规划过程中也尽量避免通过崎岖的地形,这使得三维地形特征提取变得十分困难,更为重要求的是这些提取出的特征缺乏显著性,容易出现误匹配问题。
本文以行星漫游器和着陆器地形相关导航为应用背景,提出一套三维特征提取和匹配方法,解决平坦地形条件下三维特征鲁棒匹配问题。首先在第1节中介绍基于点云邻域散布矩阵特征值的三维特征提取方法,接着将在第2节中构建基于特征间有向距离的特征描述方法,最后通过仿真实验校验所提方法的有效性。本文提出的三维特征提取与匹配方法不但可以应用在深空天体巡视采样和着陆导航定位中,还在物体识别以及SLAM(Simultaneous Localization and Mapping)中有重要作用。
1 地形特征检测
目前,三维特征检测方法主要有两类,一类是固定尺度算法,这类算法在固定的尺度下通过基于显著性的非极大值抑制(Saliency-based NMS)方法检测三维特征,如LSP(Local Surface Patches)方法[7],ISS(Intrinsic Shape Signatures)方法[8],KPQ(KeyPoint Quality)方法[9]和Heat Kernel Signature(HKS)方法[10]等;另一类是自适应尺度算法,与SIFT算法思路类似,通过生成尺度空间并选取不同的尺度自适应检测三维特征,包括Laplace-Beltrami Scale-space (LBSS)[11],MeshDoG[12],KeyPoint Quality-Adaptive-Scale (KPQ-AS)[13],Salient Points (SP)[14]方法等。此外文献[15]针对月球表面地形特征提取问题,提出采用高程数据方差检测三维特征。从特征重复检出率等性能指标来看,ISS方法是较为理想的检测方法[16]。
1.1 ISS三维特征检测方法
ISS特征检测方法的核心思想是通过特征点邻域内的点云位置协方差刻画特征点的显著性。设待考察的三维点坐标为p,q为点p邻域N(p)内的三维点坐标,那么点p对应的散布矩阵表示为
(1)
式中:M为邻域内点的个数。若用λ1,λ2和λ3分别表示散布矩阵从大到小的三个特征值,那么满足如下条件的三维点将被选取为特征点
(2)
式中:τ12和τ23是设定的检测阈值。可以看出,ISS方法的特征选取策略是从特征的显著性角度出发的,要求特征邻域内的点分布在半长轴有明显区别的散布椭球内,这使不同特征对应的描述矢量具有一定的差异,同时也使得以散布矩阵特征向量为坐标轴的特征局部坐标系更加稳定。在结构化的场景中,这种特征选取策略十分有效,但在火星、月球等深空天体表面,主要分布着陨石坑、岩石等地形特征,这些特征的主要特点是突出或凹进地表,那么根据式(2)给出的特征点选取标准,一些有效的特征地形将被剔除。因此,本文将针对深空天体表面三维地形的特点在下一节中改进ISS检测算法。
1.2 基于散布矩阵的起伏地形特征检测方法
考虑到深空天体表面地形的特点,将ISS特征选取的策略修改为
(3)
此时,只要保证特征邻域内的点具有一定的起伏,即可被选取为地形特征。同时,为了去除在一处起伏地形附近检出过多的特征点,利用散布矩阵特征值的乘积作为非极大值抑制的手段,也就是在特征点邻域内,只选取特征值乘积最大的点作为地形特征。
激光雷达或是双目相机采集三维地形,是在离散空间内进行的,运动中多次测量可能造成特征点位置在采样间隔内发生改变,因此这里用邻域内三维点位置的均值μp表示特征位置,以提高观测过程中特征位置的稳定性。
事实上,修改后的特征选取策略放宽了对特征邻域内三维点分布的要求,可以检测出更多的地形特征,但是检出特征的显著性也随之降低,这对于基于特征邻域内三维点分布或法线信息形成的特征描述方法是不可接受的,本文将在下一节建立一种基于有向距离的特征描述方法,由于采用特征间相对位置关系描述特征,因此可以有效的区分相似特征。
2 地形特征描述
已有的三维特征描述方法大多以特征附近点云空间分布或直方图等统计手段作为描述,如Johnson提出的Spin Image(SI)方法[17],Frome等提出的3D Shape Context(3DSC)方法[18],以及与3DSC相类似的SHOT(Signature of Histograms of Orientations)[19],Radu提出的Point Feature Histogram(PFH)[20]方法等。这些方法在描述密集的三维点云时都有良好的效果,但在解决稀疏点云匹配问题时,正确匹配率不理想[21]。其原因是稀疏的三维点不足以稳定的描述邻域形状,采样位置发生轻微改变就会导致特征描述符较大变化,这一现象在漫游器工作的平坦地形环境中更为严重。
2.1 三维特征间距离描述集合
为了解决稀疏点云不易匹配的问题,利用每次观测检出特征之间的距离以及特征相对位置矢量与特征主方向夹角(以下简称为方向夹角)作为基本元素,构成特征描述集合,如图1所示。这里之所以采用距离与方向夹角的集合描述特征,是由于地形遮挡以及特征检测算法重复检出率的客观限制,不能保证地形特征每次都被检出,特征数量在观测过程中是不断变化的,形成的特征描述矢量长度也不断变化,因此这里采用相对距离与方向夹角的集合作为特征描述。
事实上,如果能够保证较高的特征重复检出率,前后两次观测中大量公共特征将被重复检出,仅利用特征间的相对距离就可以很好的描述地形特征。而当重复检出率较低时(根据文献[16]中的测试结果,ISS特征检测算法对激光雷达数据的重复检出率仅有40%左右),此时由距离构成的描述集合中大部分元素将是相对新检出特征的距离,这些距离对匹配是无效的,甚至会导致误匹配率的增加。因此需要引入更多的信息加强描述集合中距离元素的“独特性”,考虑到漫游器与着陆器均工作在平坦的地形环境中,地形特征近似分布在平面内,本文选取相对位置矢量与特征主方向夹角作为辅助信息对相对距离加以区分。这里特征主方向的定义与ISS算法对主方向的定义一致,为散布矩阵最大特征值对应的特征向量。
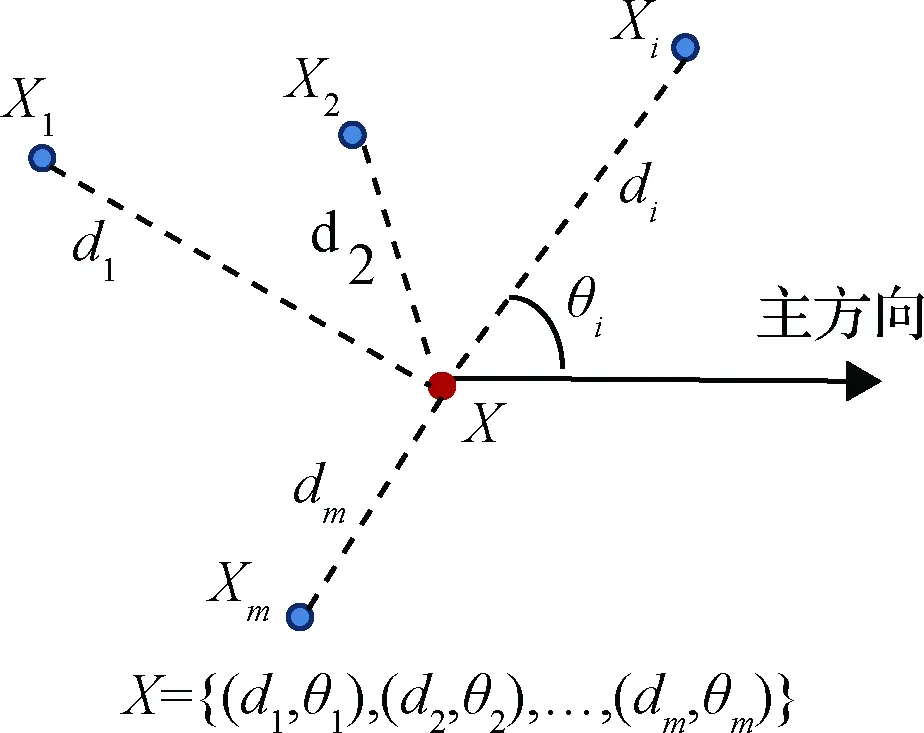
图1 特征间有向距离描述Fig.1 Orientative distance description of features
设三维特征X与其余m个同时检测出的特征之间的距离集合为{d1,d2,…,dm},结合相对位置矢量与特征主方向夹角θi,其中i=1,2,…m,特征X的完整描述为
D={(d1,θ1),(d2,θ2),…,(dm,θm)}
(4)
2.2 三维地形特征匹配
以特征间距离和方向夹角为元素形成的特征描述集合与以往的特征描述不同,无法利用多维矢量距离评估集合的相似性,因此引入集合相似理论计算描述集合的相似性。
首先给出特征描述集合元素相似性的定义
(5)
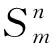
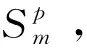
(6)
式中:τ1和τ2分别为两个设定的阈值,M为第m个特征描述集合中的元素数量。即要求相似度最高与次高的两个特征描述集合,在相似度方面应有一定的差距,同时相同元素个数应在第m个特征描述集合中占有一定的比例。
基于有向距离描述的特征匹配算法流程如下:
1)输入两次观测检出特征的描述集合,元素相似性阈值τ,以及描述集合相似性阈值τ1和τ2;
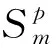
3)跳转至步骤2)直至遍历第一次检测出的全部特征点。
3 三维地形特征误匹配剔除
利用上述方法匹配的三维地形特征仍存在一定的误匹配现象,不能直接用来进行漫游器或着陆器导航,这里给出基于最小中值(Least Median Squares)的误匹配剔除方法[22]。基于最小中值的误匹配剔除算法基本流程如下:
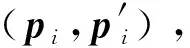
(7)
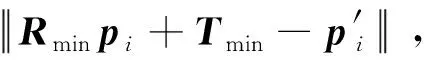
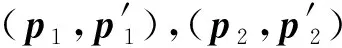
4 仿真校验
为了测试三维地形特征检测与匹配算法,生成不同起伏和粗糙程度的模拟地形20帧,模拟地形尺寸为25.6 m×25.6 m,如下图所示,并模拟LiDAR测量原理对三维地形进行采样,LiDAR的分辨率设定为256×256,最大测距距离为50 m。

图2 三维地形和模拟激光雷达测量数据Fig.2 3D terrain and simulated LiDAR measurement data
首先对本文改进的三维地形特征检测算法进行测试,考察在观测方向改变时检测算法的重复检出率。设置激光雷达绕三维地形运动,且激光雷达的光轴始终指向三维地形中心,以光轴垂直地形基准平面时的观测为参考,记此时的观测方向为0°度,观测方向每改变10°进行一次测量,直到改变50°。选取特征点邻域半径ρ=0.4 m,特征检测算法阈值τd取值由0.05至0.13。改进的三维特征提取算法平均重复检出率如图3所示。重复检出率定义为重复检出三维特征数量与 0°观测方向条件下检出特征数量的比值。特征重复检出的标准定义为,检出特征的位置经位姿变换后,与0°观测方向检出特征位置距离小于ρ/2。利用相同的模拟地形库比较了ISS算法的特征重复检出率,如图4所示,ISS算法特征点邻域半径同样设定为0.4 m,特征检测阈值设定为τ12=τ23=τISS,其中τISS的取值范围为0.5至0.9。由图3和图4可以看出改进的特征检测算法阈值取0.05时重复检出率最高,ISS算法阈值取0.9时重复检出率最高。表1给出了两种算法平均重复检出率的具体数值,改进的特征检测算法重复检出率在各观测方向条件下均高于ISS算法。
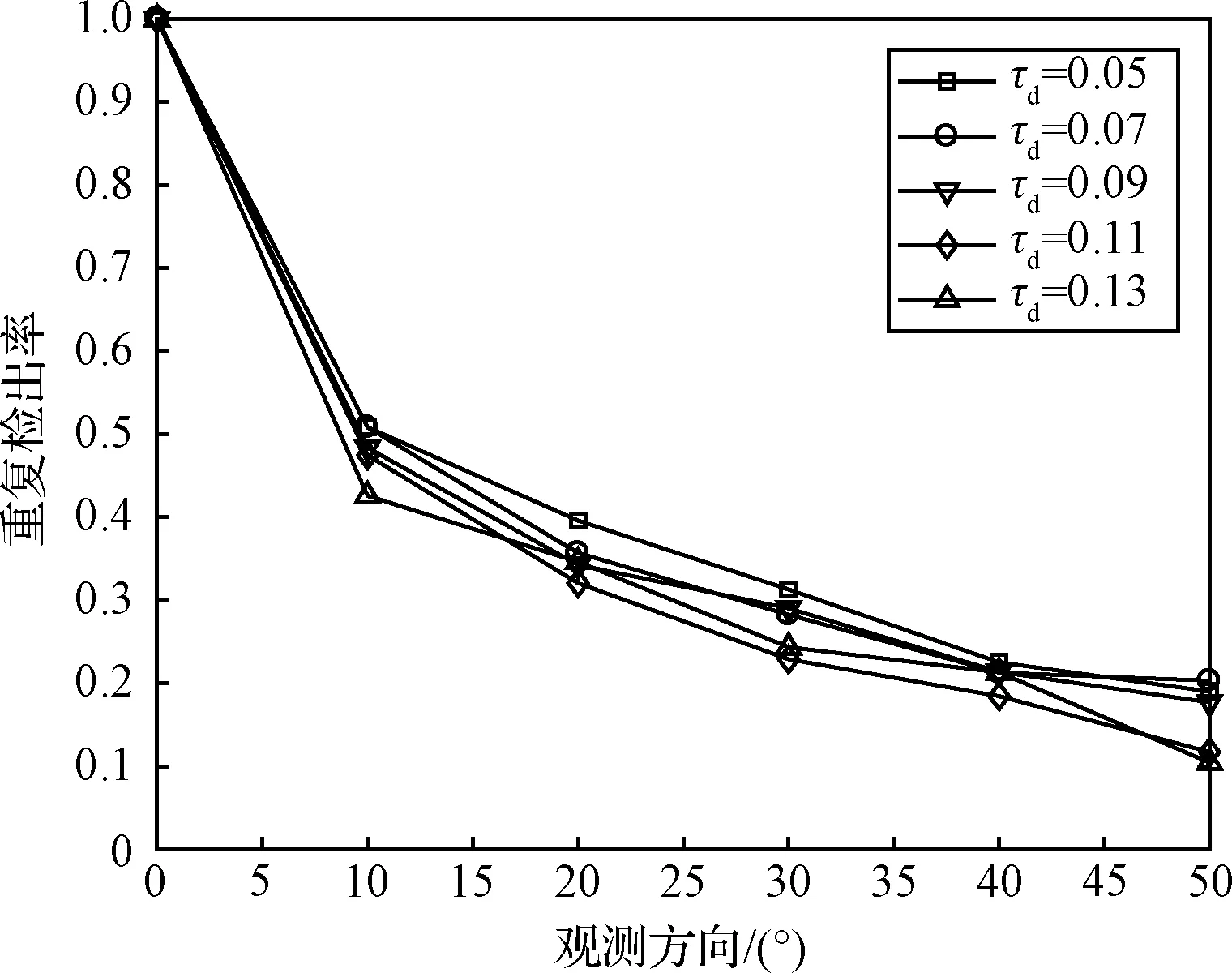
图3 改进的特征检测算法重复检出率Fig.3 Feature repeatability rate of the improved feature detection algorithm
进一步对改进的三维地形特征检测算法在不同噪声水平下的重复检出率进行测试。利用20帧模拟地形在0°至50°观测角度内模拟生成观测数据,并叠加不同水平的高斯噪声,噪声标准差包括ρ/150,2ρ/150,3ρ/150,4ρ/150和5ρ/150,特征检测算法阈值设置为0.05,不同噪声水平下的平均重复检出率如图5所示,与未加噪声的仿真结果对比
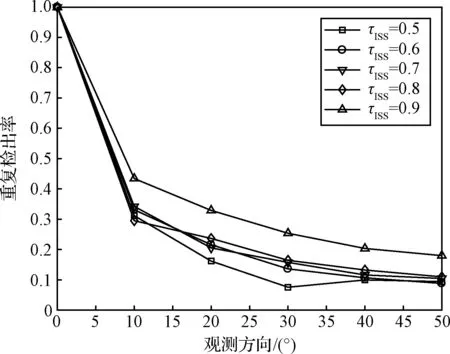
图4 ISS算法重复检出率Fig.4 Feature repeatability rate of the ISS algorithm
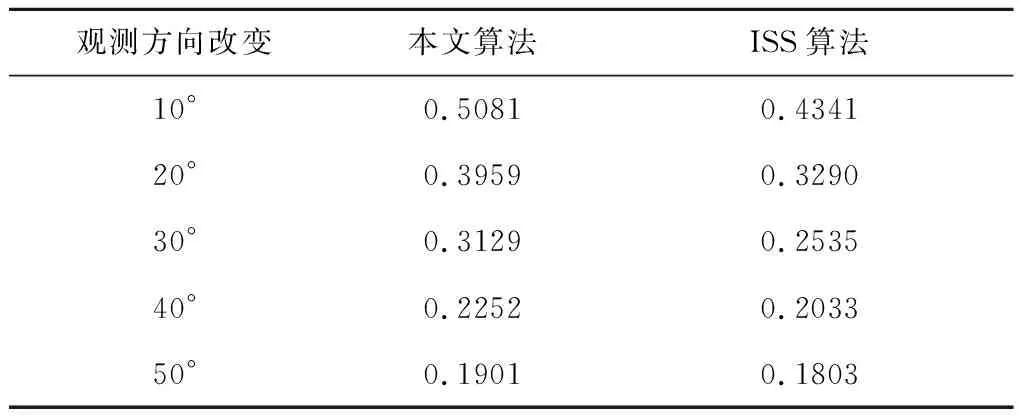
观测方向改变本文算法ISS算法10°0.50810.434120°0.39590.329030°0.31290.253540°0.22520.203350°0.19010.1803
可以看出,噪声对重复检出率影响不大。
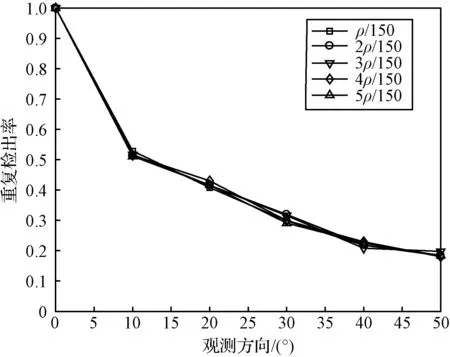
图5 不同噪声条件下的重复检出率Fig.5 Feature repeatability rate under noise conditions
接着测试基于特征间距离的特征描述方法,并与PFH(Point Feature Histogram)特征描述方法进行比较。由于这里构建的特征描述方法是基于有向距离集合的,匹配的判据是相同元素的数量是否占优,这与基于特征描述矢量距离的匹配方法不同,无法比较两种方法的PRC (Precision-Recall Curve)。因此这里仅比较两种描述方法的正确匹配特征数量,也就是基于特征间有向距离的特征描述方法在匹配时只要相同元素最多则记相应特征点匹配,而PFH描述法只要描述矢量距离最近则记相应特征点匹配,最后将根据匹配特征实际位置误差是否小于邻域半径的一半确定是否正确匹配。基于有向距离描述集合的匹配方法元素相同判定阈值设为0.1,PFH方法计算点云法线的半径设为0.1 m,两种方法的邻域半径均为0.4 m。特征检测方法采用本文改进的方法,检测阈值设定为0.05,邻域半径0.4 m。图6给出了PFH描述法和基于特征间距离的描述方法在观测方向改变且叠加不同噪声条件下的正确匹配特征平均数量。
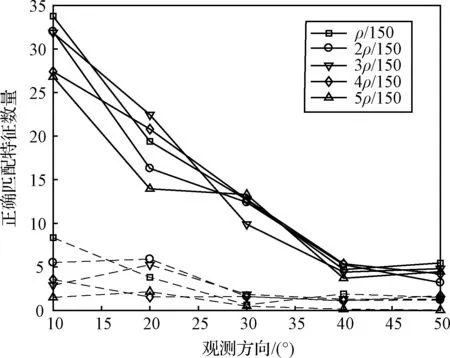
图6 正确匹配的三维地形特征数量Fig.6 Number ofthe correct matched features
图6中虚线为PFH描述方法的平均正确匹配数,只有在观测方向改变小于20°,噪声水平小于3ρ/150的情况下正确匹配数量超过3个,考虑到导航定位至少需要3个匹配特征,那么PFH描述方法在以激光雷达为敏感器的导航应用中是不合适的。图6中实线为基于特征间有向距离的描述方法在不同噪声水平下的平均正确匹配数,当观测方向改变达到40°时,各噪声水平对应的正确匹配数降到了10个以下,其余情况均有10个以上的正确匹配。不同噪声水平下的正确匹配数量均随观测角度增大而快速下降,其原因在于以下两方面:一是观测角度的增加使得部分特征由于地形遮挡而无法检出;二是倾斜的观测方向使激光雷达测量数据不均匀,在倾斜方向的远端获得的数据更加稀疏,使得特征检出率下降,且检出特征位置也不够精确。因此在导航任务中,尤其是以激光雷达获取的稀疏三维点云为观测数据的导航任务,尽量在观测方向改变小于20°的条件下应用基于有向距离的特征描述和匹配方法。
最后,应用第3节中给出的最小中值法进行了漫游器导航仿真。利用最小中值法可以剔除误匹配特征,同时也给出了两次观测间相对运动的粗略估计,在初始位置上累加相对运动即可得到漫游器位置。在图2给出的模拟地形上,设置了20个路径点,并在这些点上进行导航观测,应用三维地形特征提取和匹配方法在相邻的观测数据中确定匹配点对,借助最小中值法估计帧间运动。
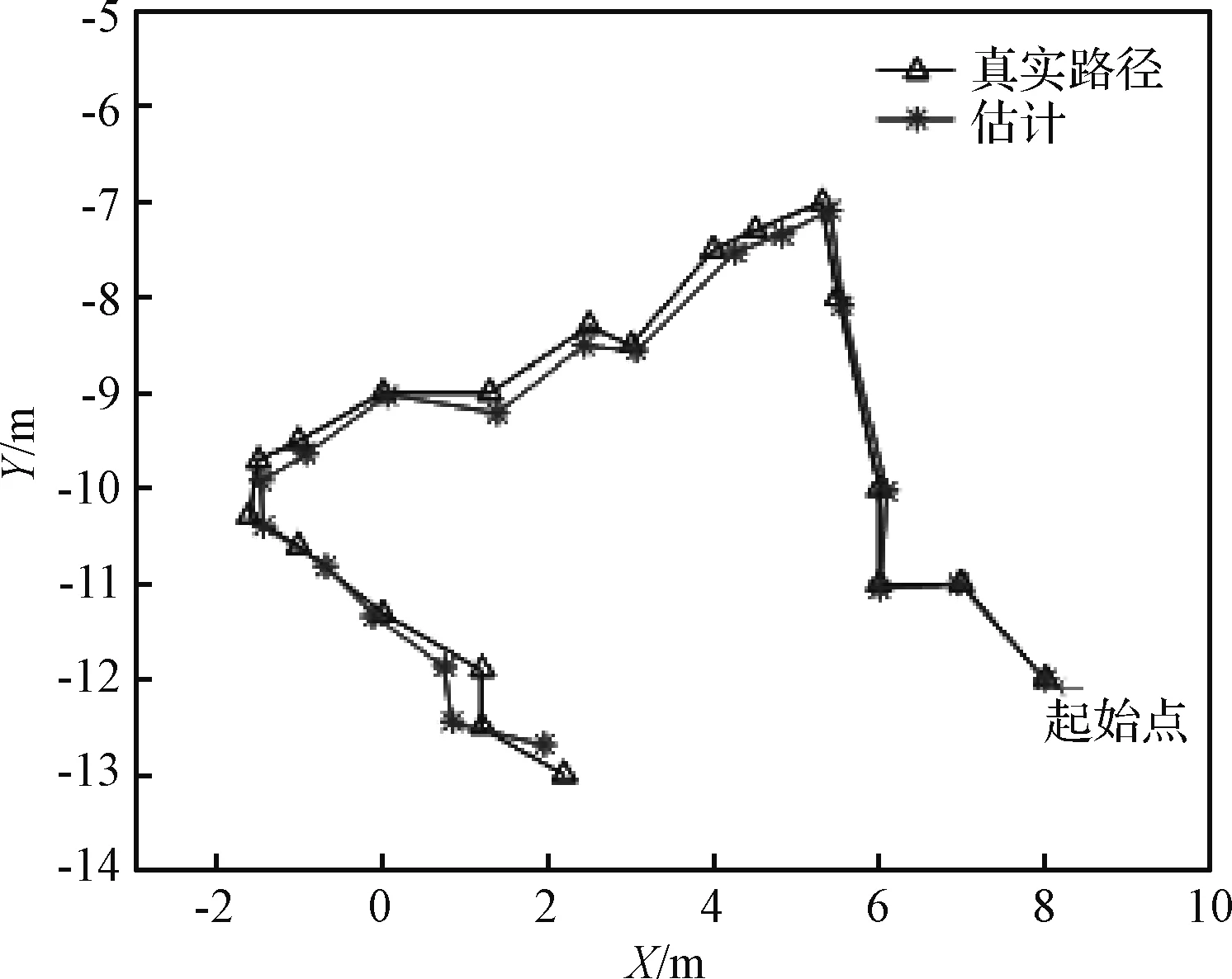
图7 漫游器定位结果Fig.7 Positioning result of the rover
图7给出了基于帧间运动估计的漫游器定位结果,开始的几次定位结果较为精确,但是由于每次运动估计的误差不断累积,在后面的路径点上导航误差不断增大。这个简单的导航仿真试验仅校验了在导航定位中应用本文提出的地形特征提取与匹配算法的可行性,如果想获得更加精确的定位结果,可以在若干次运动估计后利用全局地图进行特征匹配,提高漫游器全局定位精度。
5 结 论
针对行星漫游器地形相关导航应用,提出了一种在稀疏点云数据中提取和匹配地形特征的方法。该方法利用特征点邻域散布矩阵最大和最小特征值比检测具有凹陷或凸起的地形,提高了平坦地形中三维特征的重复检出率,为了解决稀疏点云特征匹配困难,提出了基于特征间有向距离的特征描述方法,通过与PFH三维特征描述方法的对比可以看出,利用多个特征间的有向距离集合能够有效描述地形特征,满足以稀疏点云为观测数据的导航应用需求。
参 考 文 献
[1] 崔平远, 袁旭, 朱圣英, 等. 小天体自主附着技术研究进展[J]. 宇航学报, 2016, 37(7):759-767.[Cui Ping-yuan, Yuan Xu, Zhu Sheng-ying, et al. Research progress of small body autonomous landing techniques[J]. Journal of Astronautics,2016, 37(7):759-767.]
[2] 吴伟仁, 周建亮, 王保丰, 等. 嫦娥三号“玉兔号”巡视器遥操作中的关键技术[J]. 中国科学:信息科学, 2014, 44(04): 425-440. [Wu Wei-ren, Zhou Jian-liang, Wang Bao-feng, et al. Key technologies in the teleoperation of Chang’E-3 “Jade Rabbit” rover[J]. Scientia Sinica Informationis, 2014, 44(04): 425-440.]
[3] Lauretta D S, Balram-Knutson S S, Beshore E, et al. OSIRIS-REx: Sample return from asteroid (101955) Bennu[J]. Space Science Reviews, 2017, 212(1-2): 925-984.
[4] Besl P J, McKay N D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14 (2): 239-256.
[5] Kok-Lim L.Linear least-squares optimization for point-to-plane ICP surface registration[R]. Technical Report TR04-004, Department of Computer Science, University of North Carolina at Chapel Hill, February 2004.
[6] Pomerleau F, Colas F, Siegwart R, et al. Comparing ICP variants on real-world data sets[J]. Autonomous Robots, 2013, 34(3):133-148.
[7] Chen H, Bhanu B. 3D free-form object recognition in range images using local surface patches[J]. Pattern Recognition Letters, 2007, 28(10): 1252-1262.
[8] Yu Z. Intrinsic shape signatures: a shape descriptor for 3D object recognition[C]. International Conference on Computer Vision Workshops, Kyoto, Japan, September 27- October 4, 2009.
[9] Mian A, Bennamoun M, Owens R. On the repeatability and quality of keypoints for local feature-based 3D object retrieval from cluttered scenes[J]. International Journal of Computer Vision, 2010, 89(2-3), 348-361.
[10] Sun J, Ovsjanikov M, Guibas L. A concise and provably informative multi-scale signature based on heat diffusion[J]. Eurographics Symposium on Geometry Processing, 2009, 28(5): 1383-1392.
[11] Unnikrishnan R, Hebert M. Multi-scale interest regions from unorganized point clouds[C]. Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Anchorage, AK, United States, June 23-28, 2008.
[12] Zaharescu A, Boyer E, Varanasi K, et al.Surface feature detection and description with applications to mesh matching[C]. Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Miami, FL, United States, June 20-25, 2009.
[13] Mian A S, Bennamoun M, Owens R A. On the repeatability and quality of keypoints for local feature-based 3D object retrieval from cluttered scenes[J]. International Journal of Computer Vision, 2010, 89(2-3): 348-361.
[14] Boyer E, Bronstein A M, Bronstein M M, et al. SHREC 2011: Robust feature detection and description benchmark[C]. Eurographics Workshop on 3D Object Retrieval, Llandudno, United Kingdom, April 10, 2011.
[15] 崔平远, 冯军华, 朱圣英, 等. 基于三维地形匹配的月球软着陆导航方法研究[J]. 宇航学报, 2011, 32(3):470-476.[Cui Ping-yuan, Feng Jun-hua, Zhu Sheng-ying, et al. 3D terrain feature matching based navigation for lunar soft landing[J]. Journal of Astronautics,2011, 32(3):470-476.]
[16] Tombari F, Salti S, Di L. Performance evaluation of 3D keypoint detectors[J]. International Journal of Computer Vision, 2013, 102(1-3): 198-220.
[17] Johnson A E, Hebert M. Surface matching for object recognition in complex three-dimensional scenes[J]. Image and Vision Computing, 1998, 16(9-10): 635-651.
[18] Frome A, Huber D, Kolluri R, et al. Recognizing objects in range data using regional point descriptors[C]. European Conference on Computer Vision, Prague, Czech Republic, May 11-14, 2004.
[19] Tombari F, Salti S, Di S. Unique signatures of histograms for local surface description[C]. European Conference on Computer Vision, Crete, Greece, September 5-11, 2010.
[20] Radu R B, Marton Z C, Blodow N, et al.Persistent point feature histograms for 3D point clouds[C]. 10th International Conference on Intelligent Autonomous Systems, Baden-Baden, Germany, July 23- 25, 2008.
[21] Guo Y L, Bennamoun M, Sohel F, et al. A comprehensive performance evaluation of 3D local feature descriptors[J]. International Journal of Computer Vision, 2016, 116(1): 66-89.
[22] 马颂德, 张正友. 计算机视觉:计算理论与算法基础[M]. 科学出版社, 1998: 160-161.
