光在复折射率介质界面的反射与折射

(厦门大学 嘉庚学院，福建 漳州 363105)

Snell和Descartes发现当光穿越由不同介质组成的界面时会发生折射，并总结出了Snell折射定律[1]，成为现代光学原理的重要基础。该定律被广泛应用于理解光在透明介质中的传播规律。许多学者对光在透明介质层的反射、折射进行了广泛的研究[2-4]，而在研究复折射率介质界面的反射和折射时，较广泛的处理方法是将复折射率和复角代替透明介质公式中相应的参数[5-7]，但当被扩展和应用于强的吸收材料，如金属时，这一问题至今仍未能被很好地认识和理解。Born等[8]处理了光由介质到金属边界的实折射角和路径问题，同时Garcia-Pomar等[9]依据相同的原理处理了光由金属到介质边界的实折射角公式，但是将他们得到的两组公式(介质-复折射率介质-介质)联系起来考虑，却与实验观察的结果不一致，虽然两组公式都基于相同的原理，但是由于第二组计算公式入射角是复数角，而处理过程代入计算的是实数角度，忽略了复数角对折射角的影响。所以用复折射率和复角代替透明介质各项公式中相应的参数具有一定的局限性[10-11]。

在对光散射几何光学近似研究过程中[12-19]，发现它能够克服Mie理论计算大颗粒散射振幅耗时的缺点，但也存在计算吸收性颗粒中光的传播路径和菲涅耳系数的困难。有研究者通过引入有效折射率[20-21]，给出了复折射率介质中菲涅耳系数的计算公式；也有研究者将吸收颗粒里的非均匀波近似看作均匀波，给出了弱吸收颗粒近似计算的结果，但对于吸收性稍微强的颗粒、以及强的吸收性颗粒，这种近似不再成立[18-22]。

本文研究了光在两复折射率介质界面的反射、折射规律，推导出了光通过两复折射率介质边界时的Fresnel公式，并将公式推广至任意组合界面情况下的Fresnel公式，并能够将公式退化为介质/介质的特殊情况。

1 光在复折射率介质中的传播

光在复折射率介质中的传播如图1所示，它的等幅面一般不与等相面重合，这样的波称为非均匀波，等幅面和等相面的单位矢量分别为q和s，两单位矢量之间的夹角为ξ=cos-1(q.s)。把平面电磁波E(r,t)=E(r)e-iωt，H(r,t)=H(r)e-iωt代人麦克斯韦方程，可以得到光波在复折射率介质中满足如下方程[8,23]：

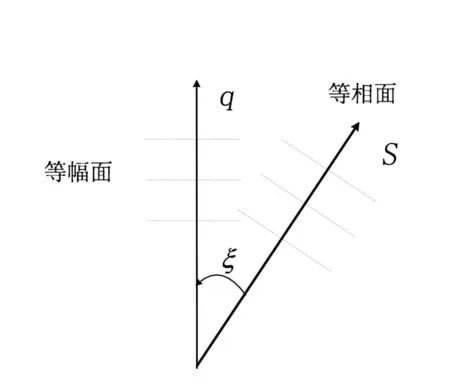
图1 光在复折射率介质中的传播

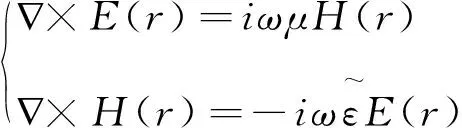
(1)

(2)

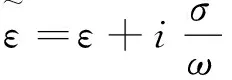
(3)

从上式可知复折射率介质的复折射率并不是真正的物质常数，而是随入射光的频率改变。同时复折射率介质中的光波可表示成：

(4)

相位常数、衰减常数与复折射率的实部、虚部之间的关系如下：

(5)

由于n，κ均不为零，从上式可知，ξ≠π/2，即两单位矢量不会垂直。经计算可得：

(6)

将参数Ns、Nq看作光在复折射率介质中传播和衰减的有效折射率，它们的大小不但与复折射率有关，还与等相面和等幅面的夹角有关。根据式(6)，复折射率介质中的光波也可表示为

(7)

将式(7)代入式(1)可得

(8)

如果Nq=0，或者ξ=0，则此时为均匀光波。

2 光在两复折射率介质界面的反射与折射

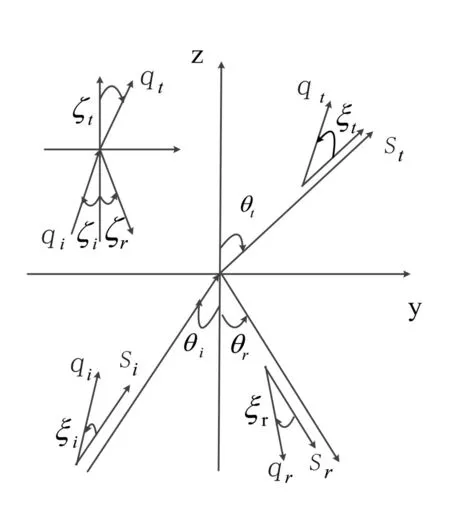
图2 光通过两复折射率介质界面的反射与折射

反射波和折射波表示为如下(r,t分别表示反射和折射边)：

(9)

(10)

根据相位的连续性条件可知，反射波和折射波的等幅面单位矢量(qr、qt)和等相面单位矢量(sr、st)也均在入射面yz平面内，θr、θt分别为反射角、折射角，反射波和折射波的两单位矢量之间的夹角分别为ξr=cos-1(qr.sr)、ξt=cos-1(qt.st)。如图2所示，并且存在：

(11)

(12)

结合(6)式，可得：

(13)

由上式可知，有效折射率Nst，Nqt除了与折射边的复折射率介质的复折射率有关，而且与入射光的入射角θi，ζi和入射光的有效折射率Nsi，Nqi有关。

3 吸收性介质边界上的Fresnel公式

在复折射率介质中电磁波不是横波，因此将电磁波分成TE波和TM波。

3.1 TE波的Fresnel公式：

对于TE波，电矢量只存在x分量。

(14)

磁矢量则包含在入射面内，因此在边界上的连续性条件为：

(15)

将式(14)代入式(15)可得

(16)

由此可得电矢量的反射率和透过率：

(17)

3.2 TM波的Fresnel公式：

对于TM波，磁矢量只存在x分量。

(18)

电矢量则包含在入射面内，因此在边界上的连续性条件为：

(19)

将式(18)代入式(19)可得

(20)

由此可得磁矢量的反射率和透过率：

(21)

3.3 特例1：透明介质-透明介质界面上的Fresnel公式

当两介质均为透明介质时，有效折射率为Ns=n,Nq=0，光波此时在介质中为横波。假定介质的相对磁导率为1(光学介质)。则公式(17)(21)简化为

(22)

(23)

(24)

与M.Born和E.Wolf所著的光学原理书上结果一致。

3.4 特例2：透明介质-复折射率介质界面上的Fresnel公式

当入射介质为非吸收性、透射介质为吸收性时，入射介质中电磁波为平面波。假定介质的相对磁导率为1(光学介质)。则公式(17)(21)简化为

(25)

3.5 特例3：复折射率介质-透明介质界面上的Fresnel公式

当入射介质为吸收性、透射介质为非吸收性时，且假定介质的相对磁导率为1(光学介质)。由于吸收性介质中光波的相位波矢与衰减波矢在界面上同时存在切向分量，折射后的波为非均匀平面波，可得介质中折射波的相位常数kst和衰减常数kqt满足如下关系：

(26)

此时折射波的衰减波矢并不等于零，根据边界条件同理可得：

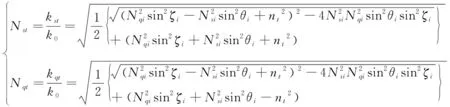
(27)

则(17)和(21)式简化为

(28)

若入射光波在吸收性介质中是均匀波时，则

(29)

则上式可进一步化简为：

(30)

对于入射介质为吸收性、透射介质为非吸收性的情况，此时折射光波是非均匀波，因此不能只是简单的将Nqt=0代入公式进行简化。

4 结论

光波在复折射率介质中传播和衰减的有效折射率Ns和Nq由介质的复折射率、等幅面和等相面的单位矢量q和s之间的夹角决定。根据光的传播表达式，传播和衰减方向分别运用相应的Snell定律，即在复折射率介质界面Snell定律可表示成两组实数形式。折射边的有效折射率除了与折射边的复折射率有关外，还与入射光的入射角和入射介质的有效折射率有关。并获得了光在两复折射率介质界面的Fresnel公式，并将Fresnel公式推广至任意两界面组合的情况下，且光通过两复折射率介质的Fresnel公式可退化为介质/介质的特殊情况。研究结果将有助于理解光在金属界面发生折射传播的路径和规律，同时对光散射几何光学近似处理复折射率颗粒边界问题具有一定的参考价值。

参考文献：

[1] SHIRLEY J W.An early experimental determination of Snell's law [J].American Journal of Physics,1951,19(9):507-508.

[2] 姚启钧.光学教程[M].3版.北京：高等教育出版社，2002：78-80.

[3] 赵凯华，钟锡华.光学[M] .北京：北京大学出版社，2003：246-249.

[4] CHIU M H,LEE J Y,SU D C.Refractive-index measurement based on the effects of total internal reflection and the uses of heterodyne interferometry[J].Applied Optics,1997,36(13):2936-2939.

[5] 陈强华，罗会甫，王素梅，等.基于表面等离子体共振和双频激光干涉相位测量的空气折射率测量[J].中国激光，2013，40(1)：180-186.

[6] 马利祥，李范鸣，牛继勇，等.基于复折射率的偏振模型及其应用[J].激光与红外，2013，43(10)：1138-1141.

[7] CHIU M H,LEE J Y,SU D C.Complex refractive-index measurement based on Fresnel's equations and the uses of heterodyne interferometry[J].Applied Optics,1999,38(19):4047-4052.

[8] 马科斯·玻恩，埃米尔·沃耳夫.光学原理[M].5版.杨葭荪，译.北京：科学出版社，1978：618-619.

[9] GARCIAPOMAR J L,NIETOVESPERINAS M.Transmission study of prisms and slabs of lossy negative index media[J].Optic Express,2004,12(10):2081-2095.

[10] 顾闻，邬云骅，陈岳瑞，等.光在金属界面的传输特性研究[J].红外与毫米波学报，2009，28(1)：31-34.

[11] 张秋长.光在金属界面传播的实折射角计算[J].厦门大学学报(自然科学版)，2015，54(2)：242-246.

[12] DAVIS G E.Scattering of light by an air bubble in water [J].Journal of the Optical Soc.Am.1955,45(7):572-581.

[13] HULST H C V D.Light scattering by small particles [M].New York:John Wiley & Sons，1957:470.

[14] HOVENAC E A.Calculation of far-field scattering from nonspherical particles using a geometrical optics approach[J].Applied Optics.1991(30):4739-4746.

[15] ADEN A L,KERKER M.Scattering of electromagnetic waves by two concentric spheres [J].Journal of Applied Physics .1951,22:1242-1246.

[16] LI X,HAN X,LI R et al.Geometrical-optics approximation of forward scattering by gradient-index spheres [J].Applied Optics.2007， 46(22):5241-5247.

[17] XU F,RRN K F,CAI X S.Extension of geometrical-optics approximation to on-axis Gaussian beam scattering.I.By a spherical particle [J].Applied Optics,2006,45(20):4990-4999.

[18] 徐峰,蔡小舒,沈嘉祺.米氏理论的近似及在粒度测量中的应用[J].光学学报,2003,23(12):1464-1469.

[19] HE H,LI W,ZHANG X,et al.Light scattering by a spheroidal bubble with geometrical optics approximation[J].Journal of Quantitative Spectroscopy and Radiative Transfer,2012,113(12):1467-1475.

[20] YANG P,LIOUK N.Light scattering by hexagonal ice crystals:comparison of finite-difference time domain and geometric optics models [J].Journal of the Optical Society of America A,1995,12(1):162-176.

[21] YANG P,LIOUK N.Effective refractive index for determining ray propagation in an absorbing dielectric particle[J].Journal of Quantitative Spectroscopy & Radiative Transfer,2009,110:300-306.

[22] XU F,CAI X S,REN K F.Geometrical optics approximation of forward scattering by coated particles [J].Applied Optics.2004,43:1870-1879.

[23]郭硕鸿.电动力学[M].2版.北京:高等教育出版社,1997：122-123.