弯曲度对弯道水流结构影响的三维数值模拟研究

于 洋，艾丛芳，金 生

(大连理工大学 建设工程学部 水利工程学院， 辽宁 大连 116024)

在自然界中弯道为河流最常见、最典型的形态。河流弯道内在的动力使得河床形态随时间变化而不断迁移，弯道内的水流形成了更为复杂的动力过程，因而弯道水流的水力特征一直是河流动力学研究的重要课题之一。自1870年Thompson J在试验中发现弯道水流同时存在着纵向和横向流动以后，许多学者对弯道水流的独特运动形态进行了广泛的研究，并取得了很多的研究成果。在20世纪50年代，罗索夫斯基[1]就系统地研究了弯道水流运动的规律。波达波夫[2]、张洪武等[3]、王平义等[4]、刘焕芳[5]和刘富强等[6]众多学者也从试验和理论分析上进行了研究，总结并导出了水面横比降和环流流速沿垂向分布的公式。近年来，随着科学技术的进步，Blanckaret K[7-11]对弯道的水流运动做了大量的研究工作。Ruther N等[12]，Khosronejad A等[13]、Zeng J等[14-15]和王青等[16]分别用不同的数值模型模拟弯道水流运动并得到较好的模拟效果。

经众多学者的研究发现弯道的几何特性对弯道水流运动及泥沙冲淤特性有着重要的影响。比较常见的几何特性有弯道宽度、弯道曲率半径、弯道弯曲度等。关于弯道几何特性对弯道水流运动影响的研究，如Kashyap S等[17]研究了135°弯道中不同曲率比和宽深比对弯道水流运动的影响。李志威等[18]用莱家谱弯道作为研究对象，研究了无量纲化的宽径比、宽深比与弯道悬沙浓度、输砂率的相关性。然而学者们[19]对于弯道弯曲度对弯道水流运动影响的研究并不多，为了更加深入地了解弯道弯曲度对弯道水流运动的影响，本文对一系列弯道的水流运动进行数值模拟。弯道模型根据弯曲度(即弯道转角)不同共分为6种，分别是30°、60°、90°、120°、150°、180°，弯道从微弯到急弯。六种弯道模型见图1，弯道宽度B=0.3 m，弯道横截面均为矩形断面，每个弯道在其上游入口和弯道出口均分别连接长为1 m的矩形直段，弯道弯曲段中心线的曲率半径为R=0.3 m，内径r=0.15 m，曲率比R/B=1，弯道底坡均为平底坡。上游入口流量为Q=72 L/s，平均流速为Vav=0.8 m/s，上游入口给定水位为0.3 m，下游出口控制水位为0.28 m，平均水深为0.3 m，弗劳德数为0.46。

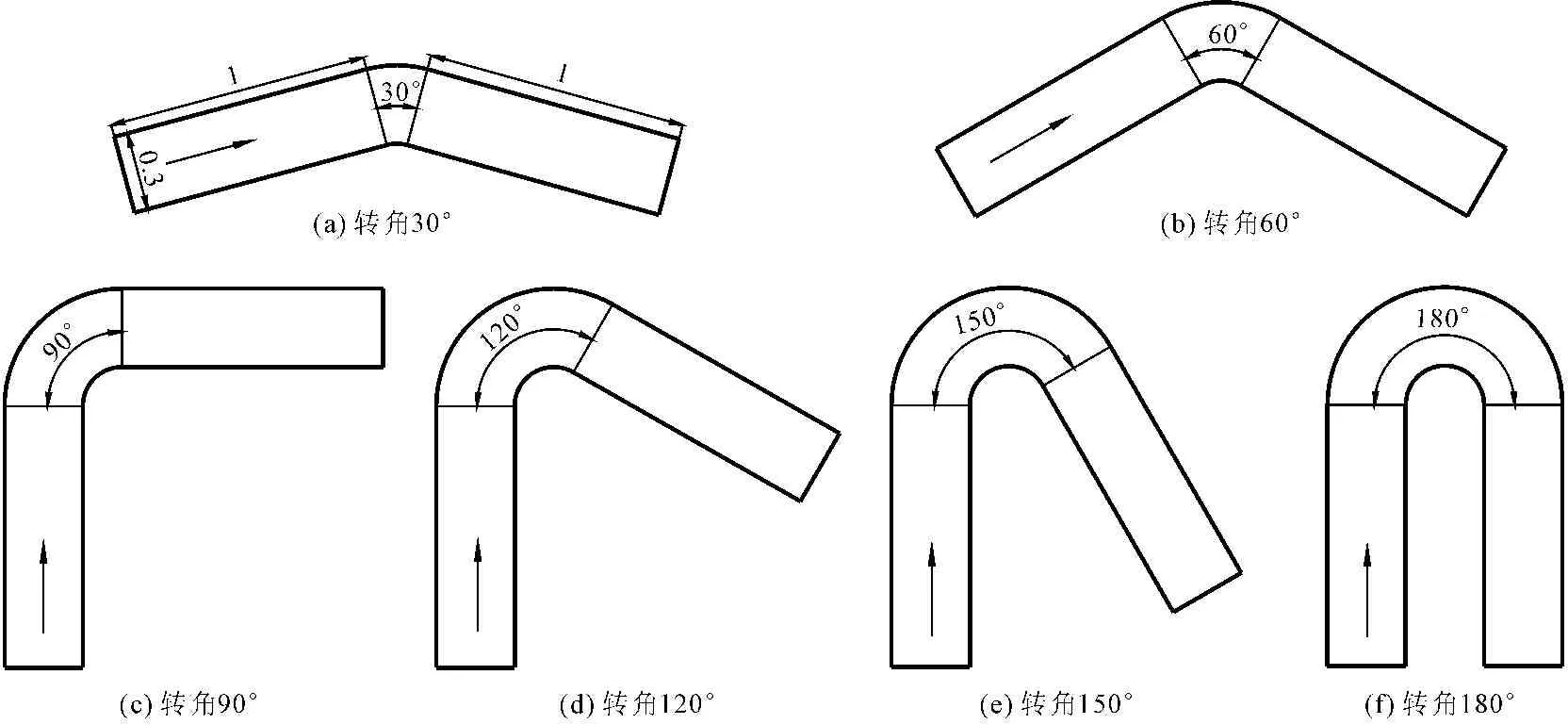
图1各弯道模型示意图(单位：m)

1 数值模型

模型的控制方程主要是连续性方程和动量守恒方程，考虑到紊流的影响，则采用k-ε方程来描述。

连续性方程：

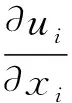
(1)

动量守恒方程：

(2)

k方程：

(3)

ε方程：

(4)

式中：g为重力加速度，m/s2；p为大气压强，kg/(m·s2)；ρ为水的密度，kg/m3；t为时间，s；c1ε、c2ε、σk、σε为特征值；l为特征长度；δ为克罗奈克函数；k为紊动动能；Vt为紊动黏性系数；ε为紊动动能耗散率；其中i、j=1、2、3。

2 数值算法和边界条件

在z坐标网格体系下，运用显—隐式交替技术对质量守恒方程和动量守恒方程进行时间和空间上的积分。数学模型采用底部适应的计算方法，采用控制体积法来计算最低的计算节点，除最低的计算节点外，采用垂向网格法来计算其他节点。对整个模型采用非结构网格的有限体积法来进行空间离散。边界条件：上游进口给定流量边界条件；下游出口给定水位边界条件。

3 模型验证

本文以经典休克莱(Skukry)矩形弯道水槽试验对模型进行验证。休克莱矩形弯道试验模型尺寸为：弯道宽度为0.3 m，高为0.5 m，内径为0.15 m，外径为0.45 m。边界条件为：上游进水口给定水位0.3 m，上游进水口给定流量为72 L/s，下游出口控制水位为0.28 m。模型水位及流速验证结果见图2、图3。

由图2休克莱弯道水位等值线图可以得知，图2(b)的模拟结果与图2(a)的实测值基本吻合，模拟结果水位的变化范围与实测值的变化范围基本一致。由图3休克莱弯道速度等值线图可以得知，图3(b)的模拟结果与图3(a)的实测数据基本吻合，但是在出口段有所出入。通过以上水位与速度的数值模拟，计算值与实测值大基本一致，所以该水动力模型是合理可靠的。

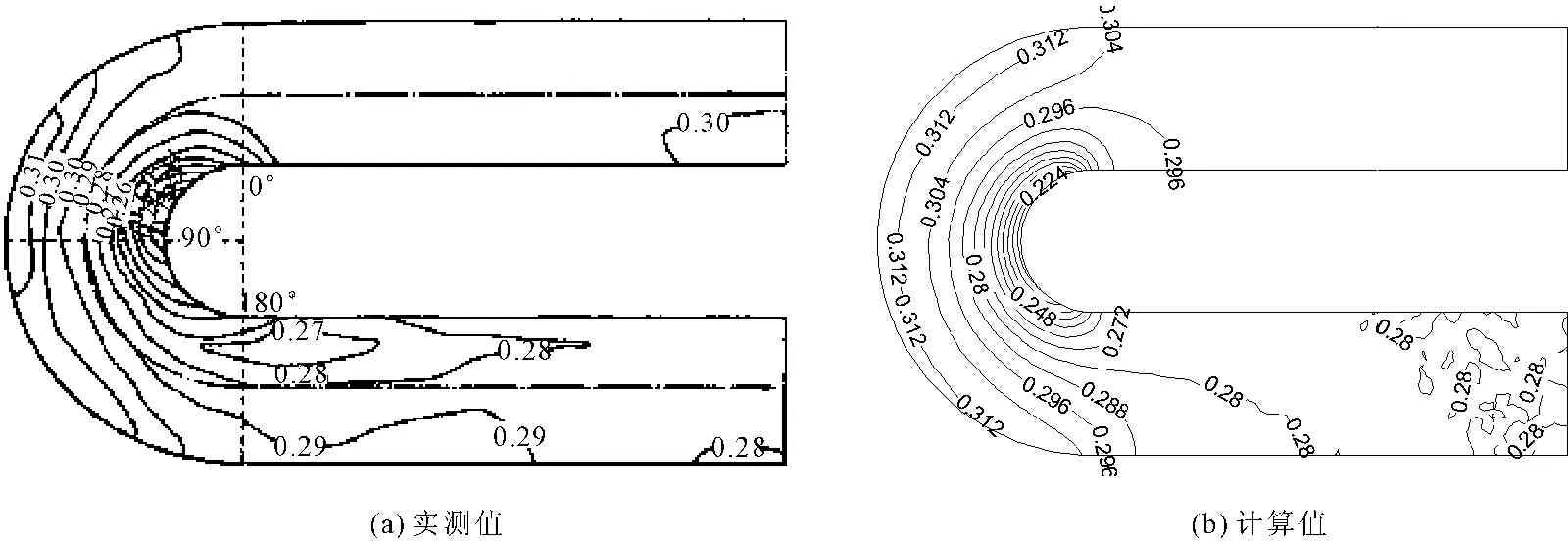
图2 休克莱弯道水位等值线图(m)

图3休克莱弯道速度等值线图(cm/s)

4 模拟结果与分析

4.1 水位

由图4可知：在边界条件相同的情况下，在各弯道入弯截面(即0°断面)，随着弯曲度的增大，水位也随之增高；在弯顶截面，靠近凹岸处的水位随着弯道弯曲度的增大而随之增加，并且弯顶处的水面横比降也逐渐增大，凸岸处水位变化较小；各弯道出弯截面(即θ断面)的水位相差较小。这说明弯道弯曲度在30°到180°之间，随着弯曲度的增大，弯道中的水面也随之增高。

表1 各弯道在断面的水面超高对比

由表1可见，各个弯道的最大水面超高一般出现在弯顶截面附近，由弯顶向上、下游两个方向逐渐减小。在每个典型截面的水面超高对比中发现，水面超高相差不大，这说明弯道弯曲度对弯道水面超高的影响较小。

4.2 流速

当水流进入弯道后，流动方向被迫转向，这使得原有的水流运动结构发生变化，流速发生重新分布，流速沿纵向、横向和水深方向均有变化。经众多学者研究发现，一般弯道水流的垂向流速远小于纵向流速和横向流速，因此可以忽略不计。但弯道的横向流速和垂向流速是弯道横向环流运动产生的重要原因。所以本文对弯道水流流速分布从横向、纵向进行分析，以及对弯道横向环流进行分析。

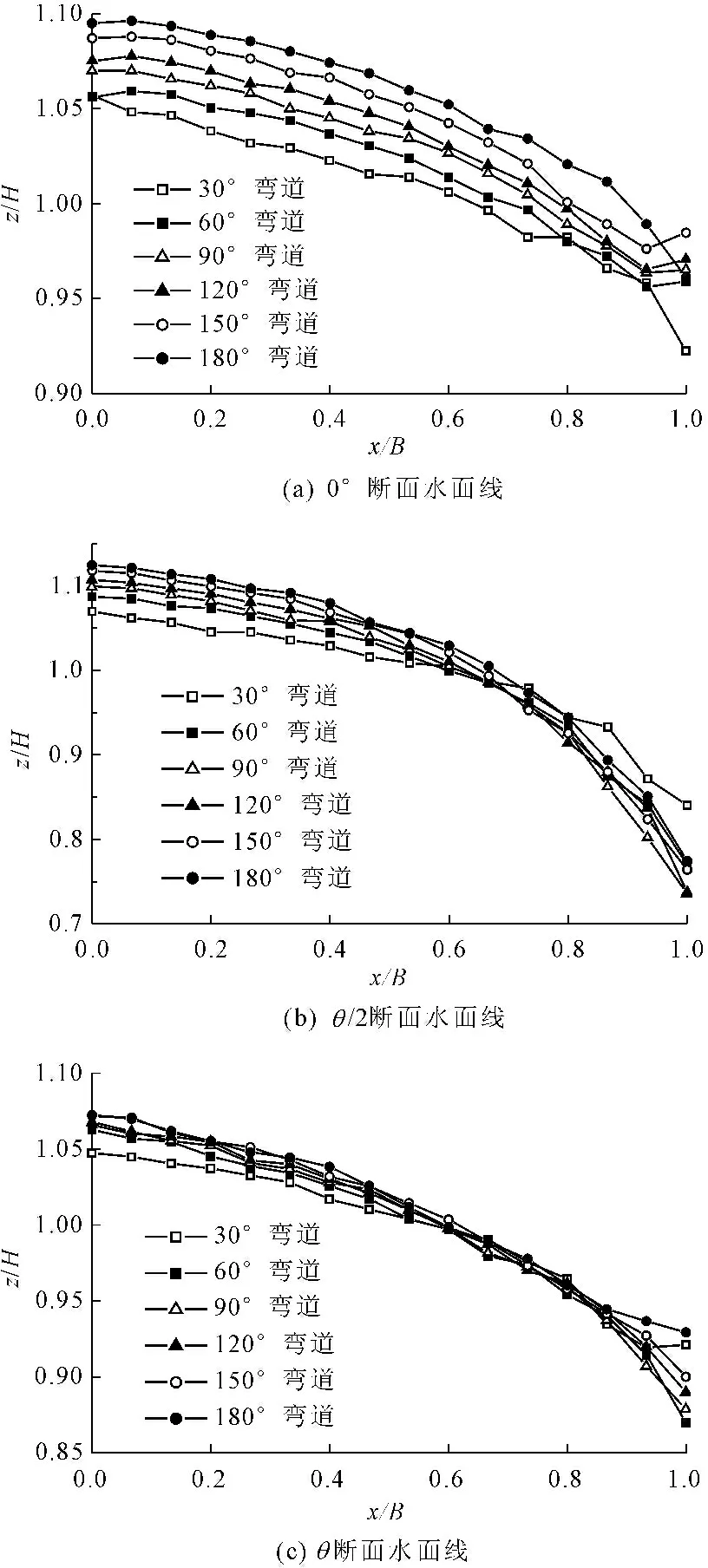
图4典型横断面水位线对比图

(1) 横向流速。弯道的横向流速和垂向流速是产生弯道横向环流运动的重要原因。为研究弯道弯曲度对弯道横向流速的影响，本文选取各个弯道的弯顶截面的横向流速进行对比分析见图5。图5中纵坐标为相对水深，横坐标为各弯道弯顶截面不同位置处的横向流速，从凸岸流向凹岸为正向的横向流速。图中x以弯顶截面的凹岸处为原点指向凸岸的相对位置。

由图5可知：弯道横向流速由凹岸向凸岸有逐渐增大趋势，弯道水流的横向运动上部有凸岸流向凹岸，下部靠近底层则由凹岸流向凸岸；在靠近凹岸侧，弯曲度越大横向流速逐渐减小；在靠近凸岸侧，弯曲度越大横向流速越大；弯道的最大横向流速出现在弯道底层并随着弯曲度的增大而增大。

(2) 纵向流速。弯道的纵向流速远大于弯道的横向流速和垂向流速，为研究弯道弯曲度对纵向流速的影响，取各个弯道弯顶截面的纵向速度进行对比分析见图6。图6中纵坐标为相对水深，横坐标为各弯道弯顶截面不同位置处的纵向流速，从水流入口流向出口为正。图中x表示以弯顶截面的凹岸处为原点指向凸岸的相对位置。

由图6可知：从弯道凹岸至凸岸，纵向流速逐渐增大，这说明主流发生在靠近凹岸侧；在靠近凹岸侧，随着弯曲度的增大，纵向流向逐渐减小；在靠近凸岸侧，随着弯曲度的增大，纵向流向逐渐增大；在弯道轴线附近，各弯道纵向流速相差较小。

(3) 横向环流。当水流从过渡段进入弯道时，由于横向流速发生变化，表层水流由凸岸流向凹岸，底层水流由凹岸流向凸岸，这就形成了横向环流。该环流和纵向流动叠加后，整个弯道水流则形成复杂的三维螺旋流。将流场中纵向流速过滤，保留垂向流速与横向流速，从而得到弯道中的环流流场图，见图7。

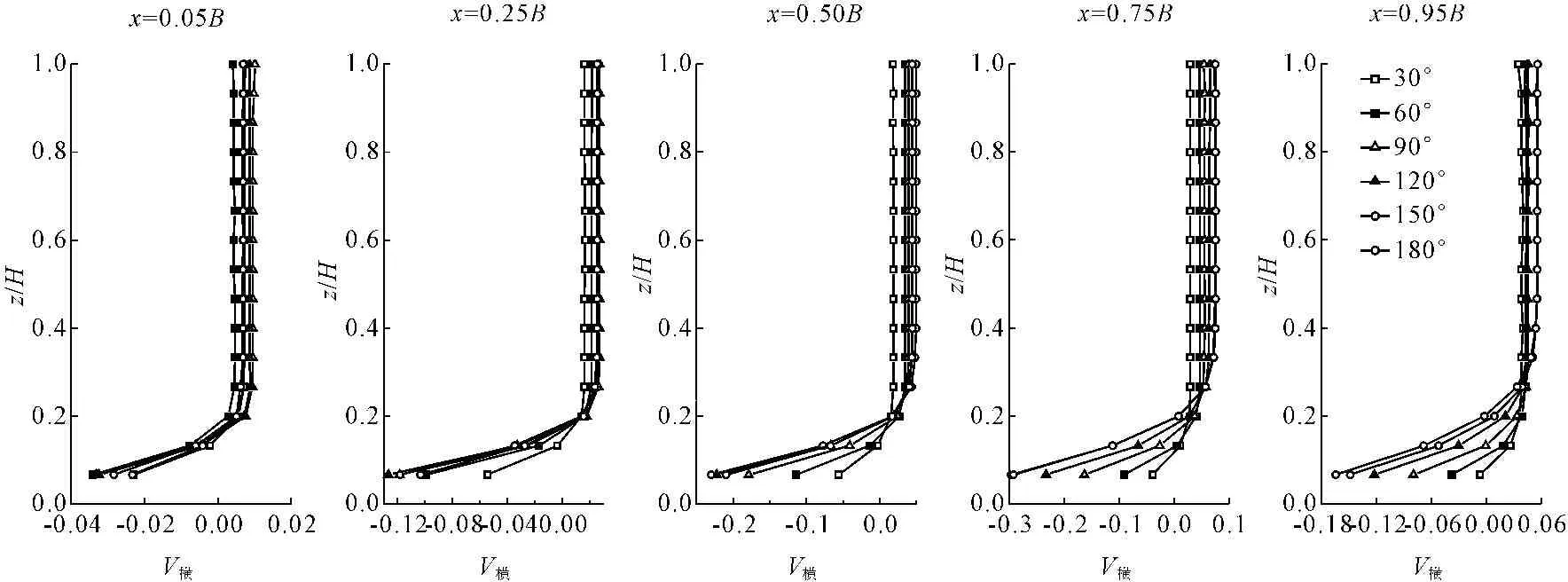
图5不同弯曲度弯道弯顶断面的横向速度沿垂向分布对比(流速单位：m/s)

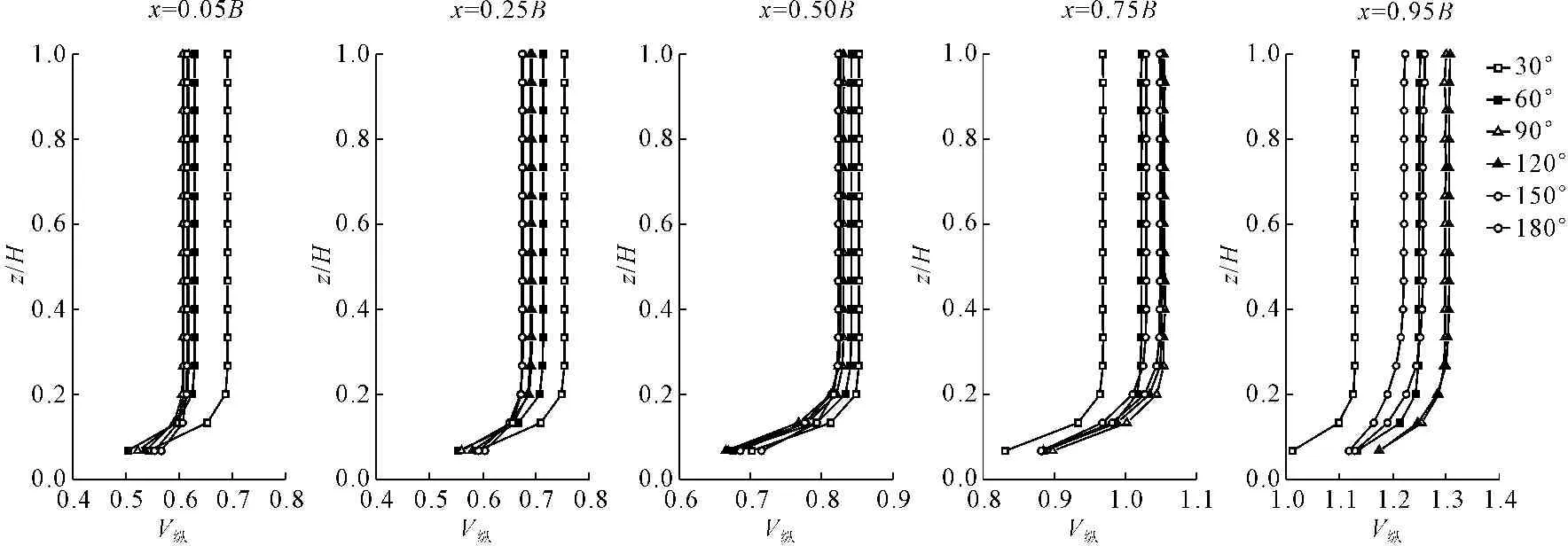
图6不同弯曲度弯道弯顶断面的纵向速度沿垂向分布对比(流速单位：m/s)

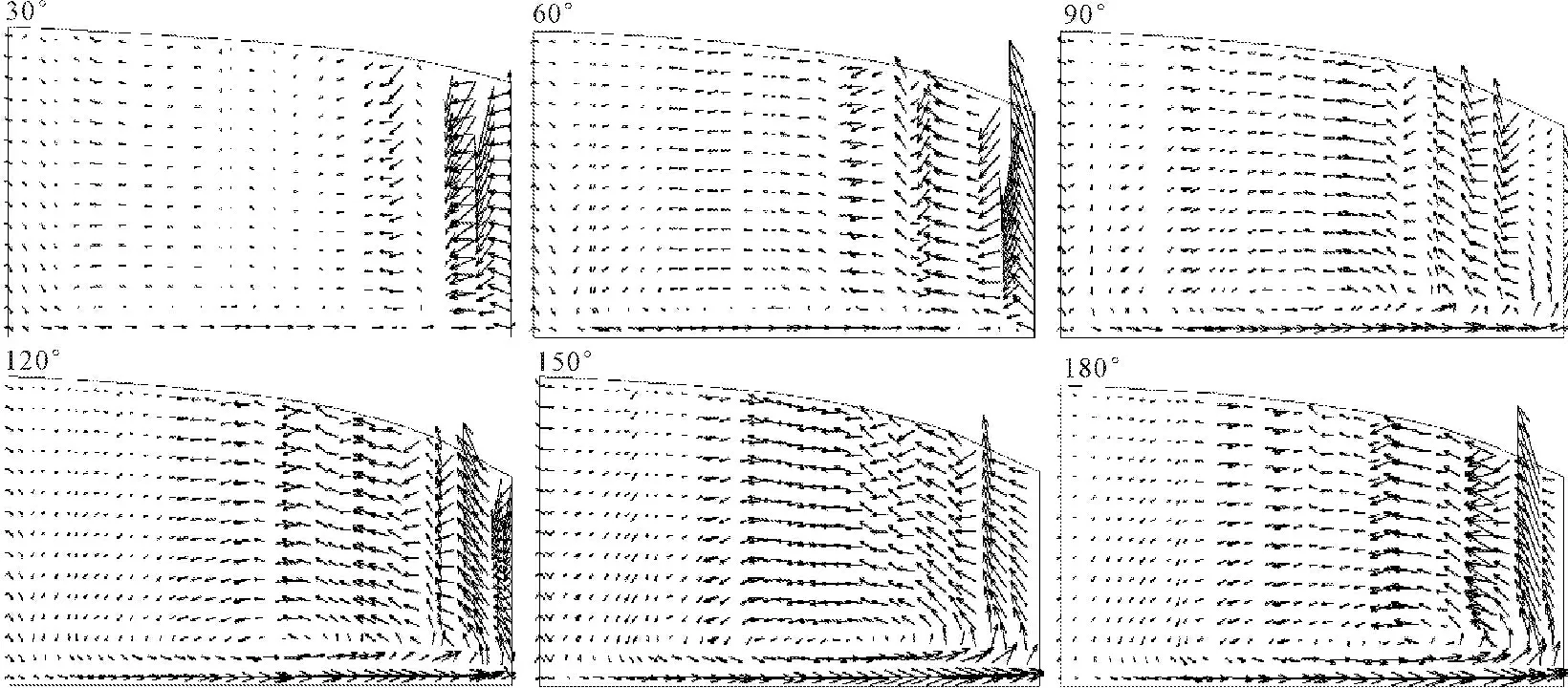
图7各弯道弯顶截面的横向环流

图7的左右两侧表示凹岸和凸岸，箭头矢量表示平面中的流速矢量。由图7可知：上层水流由凸岸流向凹岸，底层水流由凹岸流向凸岸；在凹岸附近，水流由上而下，在凸岸附近，水流由下而上且强度明显大于凹岸的水流强度，这种流速情况的存在形成了一个涡心位于偏向底层的非对称环流结构。随着弯曲度的增大，弯道横向环流强度逐渐增大，且弯道的横向环流中心位置逐渐向凸岸侧偏移。

5 结 论

本文通过对相同曲率不同弯曲度的6种弯道进行弯道水流的三维数值模拟研究。通过弯道弯曲度在30°～180°范围内各弯道中的水位变化、流速分布和横向环流的对比分析，得出以下结论：

(1) 弯道弯曲度对弯道内的水位变化有较大影响。弯道弯曲度越大，弯道内的水位逐渐增大。

(2) 弯道弯曲度对弯道中的横向流速和纵向流速有较大影响。随着弯道弯曲度的增大，在靠近凹岸侧，横向流速和纵向流速逐渐减小；在凹岸侧，横向流速和纵向流速逐渐增大；底层横向流速的大小随着弯道弯曲度的增大而增大。

(3) 弯道弯曲度对弯道横向环流也有较大影响。随着弯道弯曲度的增大，横向环流的强度不断增强，并且横向环流中心逐渐向凸岸侧偏移。

参考文献：

[1] 罗索夫斯基.弯道上横向环流及其水面形状的关系，弯道上纵向流速的分布[C]//水科院.河床演变论文集.北京：科学出版社，1965.

[2] 波达波夫.波达波夫选集：第二卷[M].北京：水利电力出版社，1958:37-41.

[3] 张洪武，吕 昕.弯道水力学[M].北京：水利电力出版社，1993.

[4] 王平义，蔡金德，方 铎，等.弯曲河道纵向垂线平均流速平面分布的研究[J].水动力学研究与进展，1994,9(3)：267-275.

[5] 刘焕芳.弯道自由水面形状的研究[J].水利学报，1990(4)：46-50.

[6] 刘富强，张晓雷，毛 羽，等.基于水沙数值模拟的某水库典型洪水过程冲淤特性研究[J].华北水利水电大学学报(自然科学版)，2016，37(5)：46-50.

[7] Blanckaert K. Flow and turbulence in sharp open-channel bend[D]. Switzerland: Ecole Polytechnique Federale Lausanne, 2002.

[8] Blanckaert K, Vriend H J De. Secondary flow in sharp open-channel bends[J]. Journal of Fluid Mechanics, 2004,498:353-380.

[9] Blanckaert K, Vriend H J De. Turbulence structure in sharp open-channel bends[J]. Journal of Fluid Mechanics, 2004,536:27-48.

[10] Blanckaert K, Vriend H J De. Turbulence structure in sharp open-channel bends[J]. Physics of Fluids, 2005,536:27-48.

[11] Blanckaert K, Graf W H. Momentum transport in sharp open channel bends[J]. Journal of Hydraulic Engineering, 2001,130(3):186-198.

[12] Ruther N, Olsen N R. Three-dimensional modeling of sediment transport in a narrow 90° channel bend[J]. Journal of Hydraulic Engineering, 2005,131(10):917-920.

[13] Khosronejad A, Rennie C, Neyshabouti S, et al. 3D numerical modeling of flow and sediment transport in laboratory channel bends[J]. Journal of Hydraulic Engineering, 2007,133(10):1123-1134.

[14] Zeng J, Constantinescu G, Weber L. 3D calculations of conditions in loose-bed open channels with significant suspended sediment load[J]. Journal of Hydraulic Engineering, 2010,136(9):557-571.

[15] Zeng J, Constantinescu G, Blanckaert K, et al. Flow and bathymetry in sharp open-channel bends: experiments and predictions[J]. Water Resources Researcj, 2008,44(9):542-547.

[16] 王 青，黄细彬.基于Flow-3D的陡坡弯道水流三维数值模拟[J].水资源与水工程学报，2016，27(5)：145-149.

[17] Kashyap S, Constantinescu G, Rennie C D, et al. Influence of channel aspect ratio and curvature on flow,secondary circulation,and bed shear stress in a rectangular channel bend[J]. Journal of Hydraulic Engineering, 2010,41(12):1423-1431.

[18] 李志威，方春明，王 亮.天然河湾水力特征与悬沙输移的关系[J].水电能源科学，2010,28(7):110-112.

[19] 谢谦城，苗伟波，戴文鸿，等.水沙变化条件下黄河下游连续弯段水流特性研究[J].水资源与水工程学报，2016，27(4)：157-161，168.