黄金椭圆与黄金双曲线
2018-07-02江苏省南京市第14中学210000
江苏省南京市第14中学 (210000) 汪 生
通过阅读文[1]、[2]以及查阅相关的资料,经过研究后发现“黄金椭圆”与“黄金双曲线”之间有着密切的联系,因此具有很多的相似性质.为了探求它们更多的性质,本文略举几例,并对部分性质进行证明,供参考.
一、相关概念
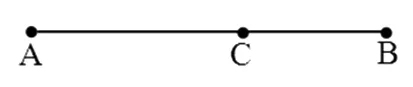
图1
1.黄金分割点:把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比,其比值为
这个分割点称为黄金分割点.如图1:

2.黄金椭圆:如果椭圆的半焦距c与长半轴长a之比等于ω,即椭圆离心率e=ω,则称这种椭圆为黄金椭圆.
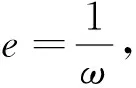
4.双曲线菱形:连接任一双曲线焦点与虚轴端点的菱形叫做双曲线菱形.
二、“黄金椭圆”与“黄金双曲线”的联系
若一双曲线以黄金椭圆的长轴端点为焦点,以黄金椭圆的焦点为实轴端点,则此双曲线为黄金双曲线.
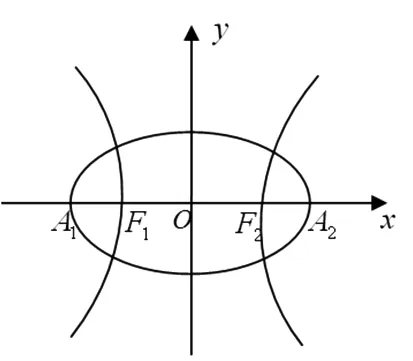
图2
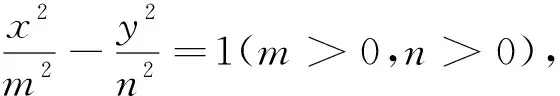
三、“黄金椭圆”与“黄金双曲线”的一些相似性质
性质1 一椭圆是黄金椭圆的充要条件是其长半轴长、短半轴长、半焦距成等比数列.
一双曲线是黄金双曲线的充要条件是其实半轴长、虚半轴长、半焦距成等比数列.
此性质由“黄金椭圆”与“黄金双曲线”的定义即可得证.
性质2 设P、Q是一个椭圆上任意两点,M是线段PQ的中点,PQ、OM的斜率kPQ、kOM都存在,则这个椭圆是黄金椭圆的充要条件是kPQ·kOM=-ω.
设P、Q是一个双曲线上任意两点,M是线段PQ的中点,PQ、OM的斜率kPQ、kOM都存在,则这个双曲线是黄金双曲线的充要条件是kPQ·kOM=ω-1.
下面证明“黄金椭圆⟹kPQ·kOM=-ω”.
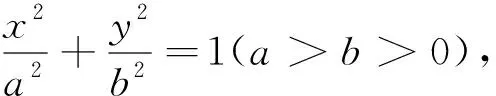
又因为点P、Q在椭圆上,所以有
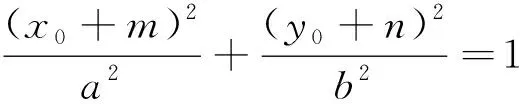
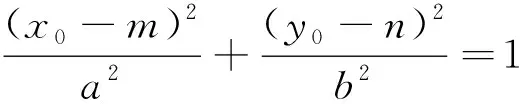
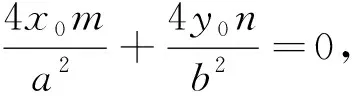
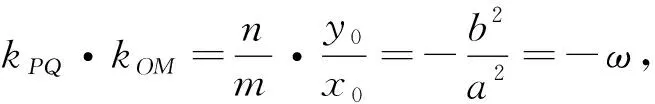
对于双曲线来说,同理可证.
性质3 设椭圆的四个顶点为A1(-a,0)、A2(a,0)、B1(0,-b)、B2(0,b),则椭圆是黄金椭圆的充要条件是菱形A1B1A2B2的内切圆过椭圆焦点.
一双曲线是黄金双曲线的充要条件是双曲线菱形的内切圆过实轴端点.
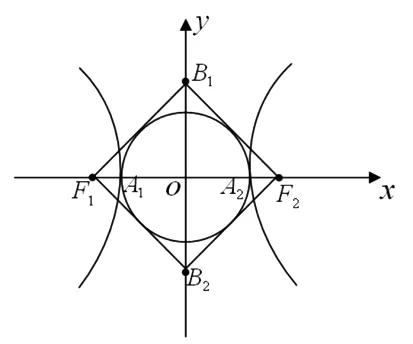
图3
对于这个性质,本人只对双曲线的情形进行证明,椭圆的情形由黄金椭圆与黄金双曲线之间的联系即可得.
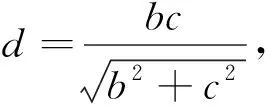
反之,易证“双曲线菱形的内切圆过实轴端点⟹双曲线是黄金双曲线”.
性质4 一椭圆是黄金椭圆的充要条件是过其焦点且垂直于长轴的直线与椭圆的交点围成一个正方形.
一双曲线是黄金双曲线的充要条件是过其焦点且垂直于实轴的直线与双曲线的交点围成一个正方形.
此性质的证明可仿照文[1]及本文的性质1得到,这里从略.
性质5 黄金椭圆上任一点与其两个长轴端点(或两个短轴端点)的连线的斜率之积为定值-ω.
黄金双曲线上任一点与其两个顶点的连线的斜率之积为定值ω-1.
此性质的证明可仿照本文性质2的证明过程.
数学是一门具有高度的抽象性和严密的逻辑性的学科.作为一名数学老师,我发现很多人不喜欢数学,总觉得数学枯燥乏味,深涩难懂.但是由以上列举的“黄金椭圆”与“黄金双曲线”的几个相似性质,我们可以充分体会到数学中的对称、统一、和谐的数学美.当我们学会了去欣赏数学美之后,就会在学习数学的实际操作中去发现美、创造美,数学中蕴含的美的因素是深广博大的,所以需要我们共同去发现、去研究.
[1]方玮.关于“黄金椭圆”性质的注记[J].数学通讯,2009(2).
[2]满新民.“黄金椭圆”性质微探[J].数学教学通讯,2006(7).
