从圆锥曲线的一个性质到“三等分角”
2018-07-02安徽省安庆一中246004陈贤清
中学数学研究(江西) 2018年6期
安徽省安庆一中 (246004) 陈贤清
用尺规三等分角与倍立方问题、化圆为方问题并称为古代三大几何难题,直到19世纪,其不可能性才被伽罗华的方程论证明.但借助于其他曲线,人们却可以利用尺规来三等分角,如借助阿基米德螺线,帕斯卡蜗线(蚶线),尼科梅德斯蚌线等.本文我们借助双曲线来三等分角.先看一个题目.
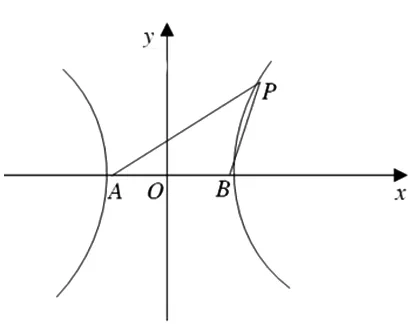
图1
题目A,B是双曲线C:x2-y2=a2(a>0)的左右顶点,P是双曲线C右支上除顶点外的任一点,∠APB=2∠PAB,则∠APB=( ).
A.15°B.30°C.45°D.60°
分析:本题初看无从下手,注意到圆锥曲线的一个性质:
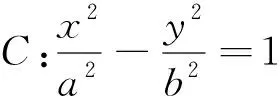
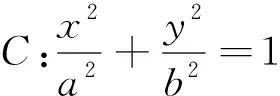
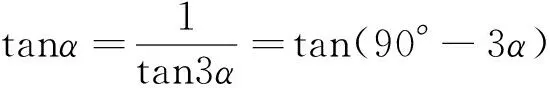
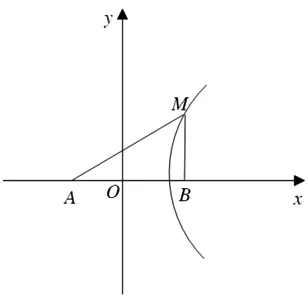
图2
拓展1 如图2所示,已知两定点A(-c,0),B(2c,0)(c>0),平面上动点M满足∠MBA=2∠MAB,求动点M的轨迹方程.
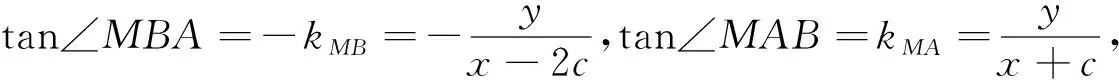
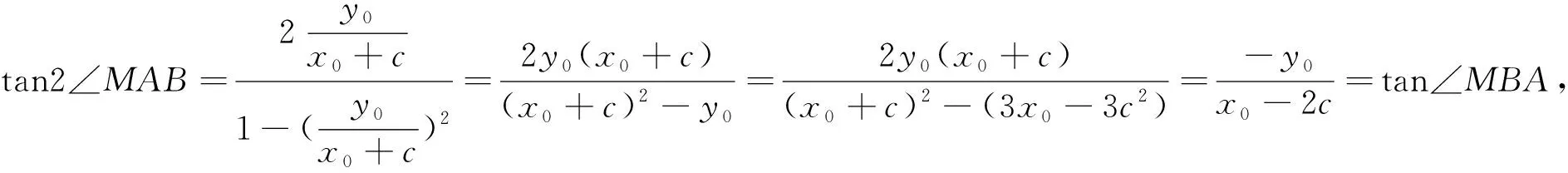
也就是说,将三角形的角度换了一个位置,满足条件的轨迹是双曲线.
更有意思的是,利用这个双曲线,我们还可以解决“尺规法三等分角”的问题.
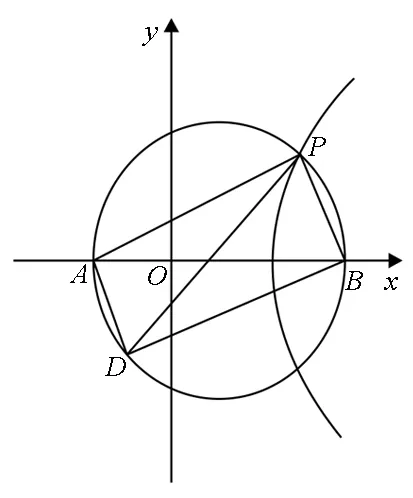
图3

