利用几何画板进行探究教学

江苏省灌云高级中学 (222200) 商再金江苏省太湖高级中学 (214125) 翟洪亮

数学软件的开发为数学教学提供检验和猜想的工具，这使我们的教学方式发生变化，可以让学生在“做数学”的实验过程中去感受、体会数学知识．数学软件几何画板(TheGeometer'sSketchpad)是以点、线、圆为基本元素，通过对这些基本元素的变换、构造、度量、计算、动画、跟踪轨迹等，构造出其他较为复杂的几何图形，其最大特点是“动态性”，给学生以直观生动的启示，促进学生对问题的理解，加深学生对问题的认识．现通过具体案例介绍其在探究教学中的使用，欢迎大家批评指正．

1 计算坐标比值，探究三点共线

指数函数和对数函数是两个重要的初等函数，它们之间存在着特定的函数关系．它们与正比例函数之间的交汇问题是学生学习中的一个难点．在苏教版高中数学必修1教材第111页的18题中，所给两个对数函数的底之间存在特殊关系，要求学生用换底公式和相似知识加以证明．

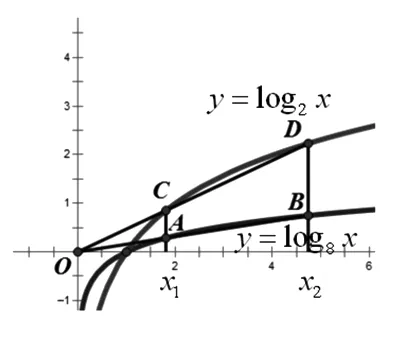
图1

案例1 如图1，已知过原点O的直线与函数y=log8x的图像交于A，B两点，分别过A，B作y轴的平行线，与函数y=log2x的图像交于C，D两点．

(1)试利用相似性的知识，证明O，C，D在同一直线上；

(2)当BC∥x轴时，求点A的坐标．

问题(1)中所给两个对数函数的底之间存在特殊关系，得到结论O，C，D三点在同一直线上．若改为一般的两个不同底的对数函数，能否也有结论O，C，D三点在同一直线上？利用几何画板进行如下探究：

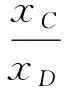
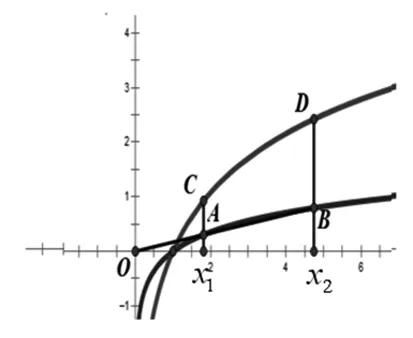
图2

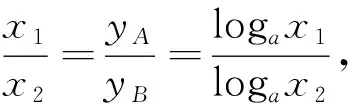
由于底数相同的指数函数和对数函数之间互为反函数，故可让学生证明：

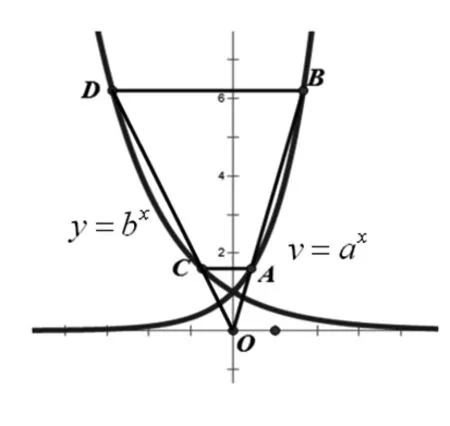
图3

结论如图3，已知过原点O的直线与函数y=ax的图像交于A，B两点，与函数y=bx的图像交于C，D两点．求证：AC∥BD．

2.拖动多点运动，演示极值性质

高考试题是经过专家组的精心命制而成，有些试题初看起来很平常，实际上却丰富多彩，蕴涵着漂亮的结论，有较大的研究空间和教学价值.我们可以利用几何画板拖动多点展示涉及多个参数问题的内在规律，激发学生探究热情．

案例2 (2016年天津市高考文科试卷第20题)设函数f(x)=x3-ax-b,x∈R，其中a,b∈R..

(Ⅰ)求f(x)的单调区间；

(Ⅱ)若f(x)存在极值点x0，且f(x1)=f(x0)，其中x1≠x0,求证：x1+2x0=0；

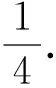
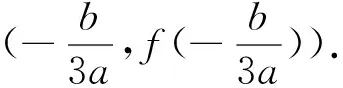
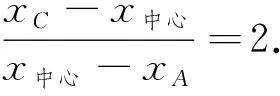
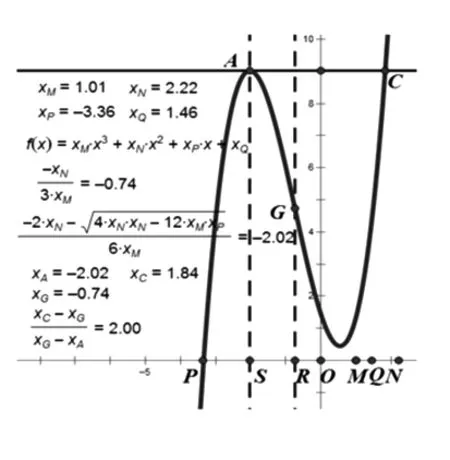
图4

证明:f′(x)=3ax2+2bx+c，因为函数f(x)=ax3+bx2+cx+d(a≠0)存在两个不同的极值点x1,x2，则方程3ax2+2bx+c=0的△=4b2-12ac>0，则方程3ax2+2bx+c=0的两根为

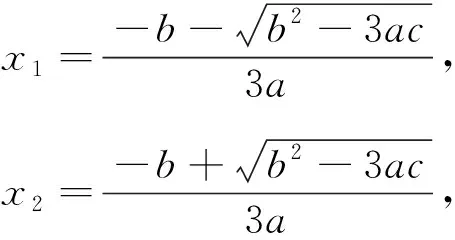
易知当x∈(-∞,x1)时，f′(x)>0，所以f(x)在(-∞,x1)上单调递增；当x∈(x1,x2)时，f′(x)<0，所以f(x)在(x1,x2)上单调递减；当x∈(x2,+∞)时，f′(x)>0，所以f(x)在(x2,+∞)上单调递增．

在图像上以极值点x1为横坐标的点记为A(x1,y1)，过点A作平行于x轴的直线AC交函数f(x)的图像于C点，则x1=xA,f(xC)=f(x1)=y1.

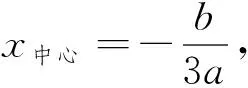
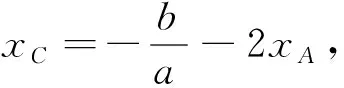
3 改变元素位置，展示图形定性

解析几何中的定点、定值问题是各地高考试卷的热点之一．对于解析几何中的定点、定值问题，可以先利用几何画板进行动画演示，然后再激发学生去证明．

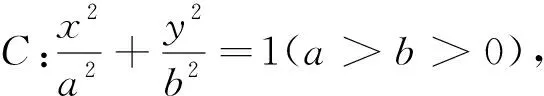
(1)求C的方程；

(2)设直线l不经过P2点且与C相交于A，B两点．若直线P2A与直线P2B的斜率之和为-1，证明：l过定点．

对于此题，给出多余条件，让学生先排除再求解．由直线P2A与直线P2B的斜率之和为-1，直线l过定点(2,-1)是在定直线y=-1上．对于此题，可以利用几何画板引导学生进行如下探究：

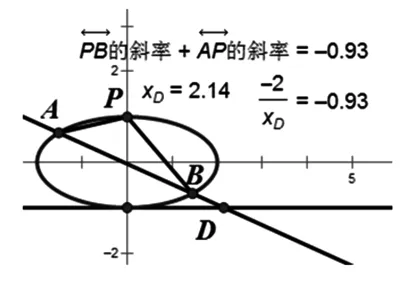
图5

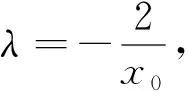
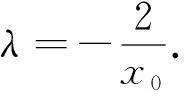
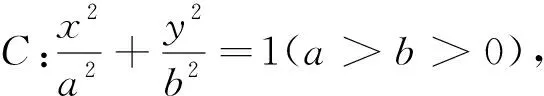
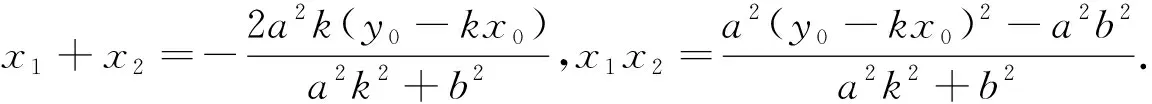
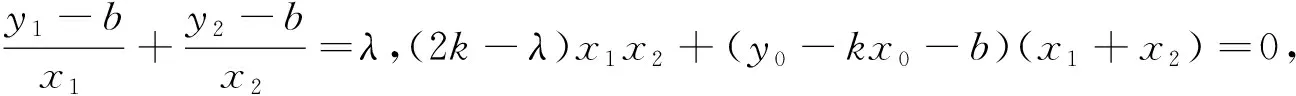
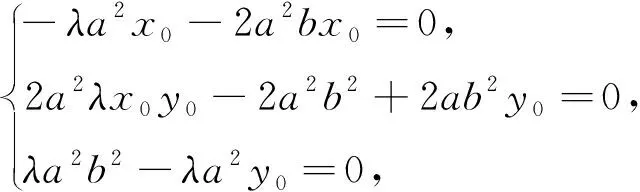
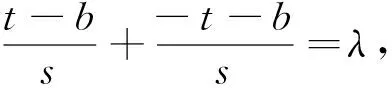
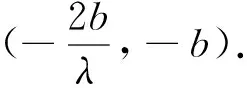
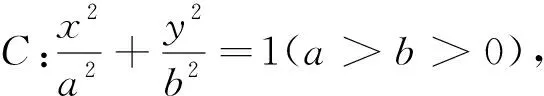
由于点P(0,b)是椭圆的上顶点，位置特殊，因此自然地联想到其他顶点时的情况，利用几何画板演示，同样引导学生探究可得：

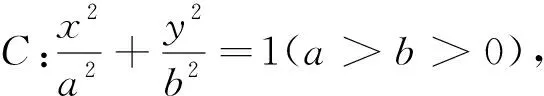
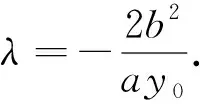
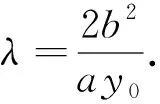
对于上述结论，可以继续让学生在圆、双曲线和抛物线中进行自主探究，去发现类似的结论，形成体系加深认识.

纵观上述案例，几何画板制作的多媒体CAI课件能够生动形象地描述教学中的复杂问题的几何关系，深刻地揭示问题的内在规律，通过探究可以培养学生思维的发散性和创造能力，激发学生学习数学的兴趣，增强学生的数学核心素养，提高课堂教学的有效性.