讲好例题
2018-07-01彭凌云
彭凌云
例题的作用老师们都知道,无需赘述。例题的讲解,老师们几乎每天都要进行,如何讲呢?我想就说说这个事。
一、先做后讲
出示例题后,老师不要急于讲解,而是先让学生独立做一会儿。老师要利用学生做的这段时间,了解学生的思路、亮点、困难处,为后面的讲解积累材料。这样做,老师的讲解才能讲到学生心坎上,引起学生思维的同步。不顾学生实情的胡乱讲解,只能是浪费时间。老师们常常抱怨,不管如何讲,讲了多少遍,学生面对同样的问题时还是出错。尽管原因是复杂的,但肯定与老师讲解例题的方式有关。因此,先做后讲非常有必要。
例如,教学“两位数加一位数、整十数”时,老师出示这个例题(如图所示)后,学生先独立做几分钟。老师巡视,看看学生有哪些做法,然后大家交流。教师再根据全班做、交流的情况,选择要讲的内容。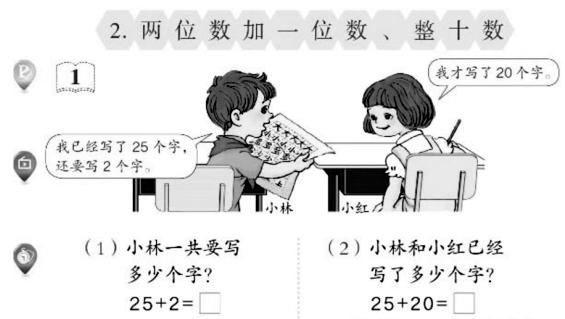
有学生说,25=20+5,2+5=7,因此25+2=27。这种方法就是教材上的,说明是学生很容易想到的方法。
也有学生说,25+2就是从25开始往后再数2,就是27。这里运用的是数数方法。虽然数数方法比较笨,但对数不大的情况还是很管用。这也说明学生对加法概念掌握得很到位。老师应该肯定,同时要指出,如果数比较大,数数就不方便了,希望孩子能够接受新的算法。
对25+20,学生也会算。25=20+5,20+20=40,40+5=45。因此,25+20=45。
这些算法,如果能出自学生之手,那么,老师再讲解将一个数分为整十数与另一个数的和,然后再加,学生记忆就会深刻得多。
二、学会分析
学生对应用题感到难,主要是难在不知从哪儿入手。而老师们讲解时常常采用的是综合法,学生虽然听起来很顺利,动起手来就受挫折。解决的办法是教分析过程,从过程中,学生学会解决的方法。要教过程,最好的方法就是分析。也就是说,从结论想起,一步步从未知走向已知,从而找到解决的方法。
例如,教学下面这道题(如图所示),教材上提示用线段图帮助思考,这是综合法。其实,从结论想起,最能训练学生的解题思路,特别是对中学、大学的学习也非常有帮助。
三、运用变式
变式教学是我国中小学数学教育的成功经验之一。高考数学命题有个原则,就是每道题都要能够从教材中找得到援引。适当运用变式,能够起到“讲一题,会一类,通一法”的作用。
例如,在一条100米长的路旁栽树,每隔10米栽一棵,可以栽多少棵樹?
像这样的题有一类:
1.一根5米长的木头,锯成1米长的一段,要锯几次?
2.一个挂钟,每到整点时响3下,一天24小时响了多少下?
这样的题,只要画个图就可以知道答案。而在教学中,有些人却弄出一大堆公式让学生记。要记住这些公式,学生都感到有难度,即使记住了,也容易出错。
又如,在学习连加法时,教材上有这样的题:9+1+2=?。到期末复习时,可将此题变为:在9、1、2的1与9、1与2之间填上+或-,并计算结果。老师要举例向学生解释题目的意思,如可填为:9+1-2。学生独立做后,老师讲解下面的内容。
当都填+时,结果是:9+1+2=12。
当都填-时,结果是:9-1-2=6。
当前面填+,后面填-时,结果是:9+1-2=8。
当前面填-,后面填+时,结果是:9-1+2=10。
这样的变式题不难,对培养学生的思维能力非常有帮助。
四、适度拓展
小学生学的数学知识还很少,不能过度拓展。否则,学生听不懂。适度拓展有利于学生对知识的理解,还能开拓思维,帮助学生掌握数学学习的方法。老师们要充分利用教材,设计好拓展内容。
例如,教材上有关于哥德巴赫猜想的阅读材料,由此,可设计如下两个题:
1.6=3+3,8=3+5,10=3+7=5+5,请仿照这样的方式,将12,14分别写成2个奇素数的和。
2.9=3+3+3,11=3+3+5,13=3+5+5,请仿照这样的方式,将15,17分别写成3个奇素数的和。
又如,学了三角形的内角和是180毅,可设计这样的拓展题:
根据三角形的内角和是180毅,求出四边形、五边形、六边形的内角和。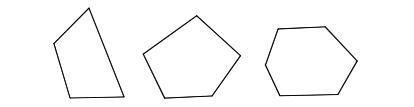
如何思考?千万别告诉小学生多边形的内角和公式,而是要引导学生想:要求四边形内角和的度数,没有现成的公式,在哪儿见过与图形有关的度数?直角是90毅,平角是180毅,三角形的内角和是180毅,周角是360毅。四边形中能找得到这些度数的角吗?直接找不到呀。怎么办?变出来!如何变?观察图形,变三角形最好,那就连线吧。这样连接对角线,就将四边形变成了2个三角形,由三角形的内角和是180毅容易知道四边形的内角和是360毅。四边形解决了,对五边形、六边形,学生仿照这样的方法也能求出内角和。
(作者单位:长沙市岳麓区博才卓越小学)
