涵养学生理性精神
2018-07-01

娄底市第六小学原名涟钢一小,始建于1968年。经过几十年的发展,如今已成为一所全市较高标准的现代化示范性小学。学校数学组长期开展“问题导学”研究,取得了显著成效。
因果溯源。著名数学教育家弗赖登塔尔曾经这样描述数学:“没有一种数学的思想,以它被发现时的那个样子公开发表出来。一个问题被解决后,相应地发展为一种形式化技巧,结果把求解过程丢在一边,使得火热的发明变成冰冷的美丽。”数学组老师们试图通过自身的努力,把人类积累的数学知识体系、把数学的形式化逻辑链条还原为当初数学家发明创造时的火热思考,从而提出“是什么?为什么?”这样触及数学本质的问题。
例如,用有序数对表示物体(点)在平面中的位置,其实质是在直角坐标系中,对于平面上的任意一点,都有唯一的一个有序数对与它对应;反过来,对于任意一个有序数对,都有平面上唯一的一点与它对应。
在教学中,我们常见这样的设计:第一步,用生活情境引入,先出示班级学生座位图,然后让学生分别说说自己的座位在教室里的第几行、第几列。第二步,学生思考有没有更简单的表示方法,教师逐步引导学生得出表示点的位置的方法,即先看点在第几列,再看在第几行,最后按先横后纵的顺序标出数对。第三步,完成教材及练习册中配套的习题。
以上的教学设计之所以易于被老师们所采纳,是因为教材就是这样呈现的。但显然学生在学习过程中缺乏数学思考的激情,也难以体会(a,b)这种数对形式表示平面上点的位置的奇妙之处。因此,我们做了下面的设计:
师:(出示课件下图)这是我们熟悉的数射线,观察这个点的位置,它表示几?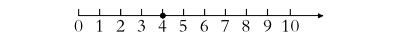
生:4!
师移动这个点至7、9的位置,学生都能说出点的位置。
师:(出示课件下图)还是这个点,它这会儿不在数射线上了,而是在平面上,它的位置应该如何表示呢?
生1:还是用4吧?
生2:好像不行,因为它在数射线的上方了,应该和刚才在线上的点不同。
生3:就写成“4的上面”吧。
生4:也不对呀,4的上面那么多位置,大家都写成“4的上面”就不太好了。
生5:是呀,如果这个点再往上移,那不是得写成“4的上上面了”?
生6:得看往上移的距离才好确定了。
师:说得好像有道理!
生7:是的,如果这个点往上2格,我们就记作“4上2格”,如果是4上面3格,我们就记作“4上3格”。
师:看来,要确定一个平面上点的位置得用两个数才行!那有没有办法让大家一看就明白,这个点到底在4上面几格呢?
在上面的问题设计中,教师的出发点就是退回到数对发明时最初的样子,让学生有机会亲历这个发明的过程。在这个曲折但又生动有趣的过程中,学生享受到了再创造的快乐。正如苏霍姆林斯基所说:人的内心深处有一种根深蒂固的需要———总感到自己是发现者、研究者、探寻者。在儿童的精神世界中,这种需求特别强烈。但如果不向这种需求提供养料,即不积极接触事实和现象,缺乏认识的乐趣,这种需求就会逐渐消失,求知兴趣也会与之一道熄灭。
因势利导。数学教育家郑毓信先生说:“设问应合乎情理,力求自然。”也就是说数学教师设计的问题应贴近学生的知识实际、能力实际、生活实际,抓住问题的本质,突出重点,体现知识的发生、发展过程,使学生学到可以理解的、可以学到手的和可以推广应用的数学。
“3的倍数的特征”是人教版教材五年级下册的内容。3的倍数要根据各个数位上的数字之和是否是3的倍数来判断,而先前学习的2、5倍数的特征只要看个位上的数来判断。看上去,新知与原有经验有些不一致了,于是,学生思考后提问:“我怎么才能知道什么时候只需要看个位,什么时候需要看各个数位上的数字之和呢?”这个问题是学生基于最自然的思考路径提出来的。因此,我们在进行问题设计时,就因势利导:判断一个数是不是2、5的倍数,只要看个位上的数字是不是2、5的倍数,而判断一个数是不是3的倍数,却要看各个数位上的数字之和是不是3的倍数。这是为什么呢?带着这个问题,请同学们自己阅读下面的学习材料。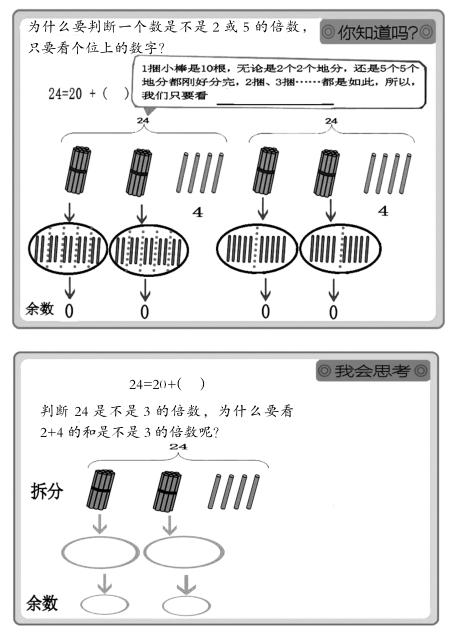
課的最后,学生利用已有的经验,成功地找到了4的倍数的特征。就找到一个数的倍数的特征本身而言,这不是太重要的事情,重要的是学生学会了触类旁通地学习数学的方法,以及凡事都要追问为什么的研究态度与理性精神。
因树为屋。这里借用因树为屋的本义依树架屋。依什么树呢?阅读之树!因为好的问题设计还来源于数学教师的专业功底,因此,阅读显得特别重要。数学组老师们常常带领大家深度阅读教育经典的深度阅读活动。老师们读的书多了,视点也就高了,视野也就宽了,设计的好问题自然也多了。
例如,张奠宙先生的《按“四基”的要求编写教材———以抽屉原理为例》一文中指出,“抽屉原理的真正意义应该在于丢开穷举检验,诉诸逻辑论证”。这个观点颠覆了我们之前的认识,我们深度反思,提出了这么几个问题———
导入部分:借用唐代诗人贾岛的《寻隐者不遇》,“松下问童子,言师采药去。只在此山中,云深不知处。”诗句告诉我们师傅一定在这座山中,只是“云深不知处”。在数学上,也有这样一类问题。比如:“把4个苹果放在3个抽屉里,总存在一个抽屉,它至少有2个苹果。”这句话是什么意思,你懂吗?你信吗?
练习部分:
4个苹果放入3个抽屉。
辨析:①有一个篮子里至少有3个苹果,对吗?②有一个篮子里至少有1个苹果,对吗?③“有一个篮子里至少有2个苹果”与“有一个篮子里至少有1个苹果”哪一个更好,为什么?
在实施问题导学的数学学习活动中,好奇心是数学学习的重要动力源泉,学生在好奇心的驱动下主动学习,发现问题、提出问题、解决问题的能力逐渐增强。特别值得一提的是,学生的那种穷究到底的精神、用事实说话的品质得到沉淀。所有这些,都是孩子们未来生活中不可或缺的品质。
“为孩子未来的发展而教”,我们娄底六小数学组将继续以此为目标,精心设计每一个问题,精心上好每一堂数学课,让更多的孩子爱上数学,让更多的老师爱上数学教育。
(执笔:李爱容、谢凌云、袁运飞)
