图形的运动(三)教学研究报告
2018-07-01
一、问题
人教版数学教材五年级下册的图形的运动(三)单元是学生在认识生活中的旋转和平移现象,会判断一种物体的运动是平移还是旋转的基础上进一步学习的内容,同时它也是图形的运动教学中的一个难点———在小学阶段的图形运动中,学生最难掌握的就是旋转。教学中,要求学生能在方格纸上把一个简单的图形按照顺时针方向或逆时针方向旋转90度。在实际操作中,学生画图时总是频繁出错,老师们对此也做过不少的研究和尝试,其中常见的方法是把平面图形的旋转分解成线段的旋转,还有老师会进一步把旋转和钟面结合,帮助学生理解。
1.关于教材的编排
新教材在编排这一部分内容时新增了例题2,是对旋转———刚体变换(变换后不改变物体任何两点之间的距离以及点之间构成的线段的夹角不变)的研究。通过对教材的分析和解读,我们认为三个例题是层层递进的关系:例1是学习旋转的三要素,这是研究旋转现象的基础;例2是研究旋转过程中中心点的位置不变,经过中心点的两条线段都旋转了90毅,从编排中可以看出是为例3的画旋转图形做铺垫。笔者认为在教学例2时还需要补充对旋转的刚体变换的研究,这样将更好地帮助学生掌握画图的技能。
2.关于学生的认知起点
为了切实掌握学生的学习起点,笔者对学生进行了学前调研(如图1)。调研结果显示:(1)在旋转现象的调研中,90%以上的学生能准确地说出风车的运动是旋转现象,可是有39.3%的学生描述停车杆和秋千的运动是上下运动、左右摆动等,还有13%的学生认为是平移现象。这是来自于学生已有认知中的错误。二年级第一次认识旋转现象时,教材中给的素材全部是像风车这样旋转一周的素材,老师们提供的素材也大多如此,难免给学生造成只有旋转一周才是旋转现象的错误印象。(2)在三要素的调研中,尽管只有极少数学生能准确完整地描述旋转过程(占比约为5%),但是绝大部分学生能关注到三要素之一,其中能够用旋转角度和方向描述运动过程的分别达到35.7%和42.9%。由此可以看出,对于三要素,学生有一定的经验基础。
在对教材和学生进行充分解读后,我们确定本节课的教学目标为:
1.学生在已有经验的基础上,完善对旋转三要素的认识,能用中心、方向和角度描述旋转过程,并且能够用它们判断旋转现象。
2.学生在观察、思考中明白:旋转的三要素确定了,旋转的结果也就确定了,明确三要素的内在意义。
3.通过观察、想象、验证等活动,学生自主探究图形旋转的特征:旋转后图形的形状和大小不变;对应线段的夹角等于旋转角度,为画旋转图形积累经验。
4.学生通过观察建立表象,借助表象展开想象,培养空间想象能力。
二、实践
基于以上思考,我们进行了教学实践,主要教学过程如下:
(一)回忆预学,引入探究
师(出示课前预习单):上课之前,我们做了预学单。对于图形的运动,我们已经认识了三种图形的运动方式:平移、旋转、轴对称。你觉得指针的运动是哪一种呢?(生:这是旋转)在描述指针的旋转过程时,同学们都是怎么想的呢?一起来看看。
(二)操作感悟,理解旋转
1.理解旋转的三要素
师:请仔细观察这个同学的预学单(如图2),他在描述指针的旋转时说出了什么?(生:角度)我们请他说说是怎么想的。
生1:钟面上从12到3的角度是90毅,一共有3个大格,所以每个大格是30毅。
师:你可真会计算,指针走一大格就是30毅,度是一个计量角的大小的单位,那你从这儿看到一个角了吗?它的两条边在哪里呢?
生1:指针原来的位置和现在的位置可以看成角的两条边。
师:大家想象一下他说的角在哪里。谁能上来找给大家看一下?(生上台指角)你们找的是一样的吗?你们看到的角,一条边是指针原来的位置,另一条边是指针旋转后的位置。在数学上,這个角就叫旋转角。这个同学在想象运动过程时关注到了角度,我们把他的想法记下来。(板书:角度)我们继续来看,(出示图3)这个同学说出了什么?你知道顺时针方向是什么意思吗?
生2:就是钟面上时针运动的方向,从12开始到1,再到2,这样转下去就是顺时针方向。
师:是的,在数学上,我们习惯用顺时针方向和逆时针方向描述图形的旋转。(出示图4)有些同学不太能理解为什么是顺时针方向,谁能想个办法给他们说清楚?
生3:图4中停车杆的运动可以看成钟面上指针从9到12,这还是顺时针方向。
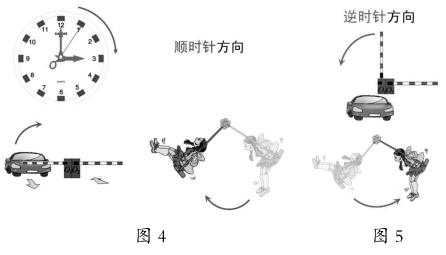
师:是的,它就相当于钟面上从9旋转到12,这就是顺时针方向。与顺时针方向相反的方向是逆时针方向。(出示图5)秋千荡过去是顺时针方向,荡回来就是逆时针方向。刚才这些同学关注到的是方向,我们也把它记下来。(板书:方向)在描述旋转过程时,这个同学指出了指针绕O点旋转(出示图6),你能和大家说说绕O点旋转是什么意思吗?
生4:O点固定不动,然后指针围绕着它转动。
师:那是不是和她说的一样呢?(课件演示)请仔细观察,指针在旋转的时候,O点的位置有没有动?(没有动)你觉得这点有什么作用?(可以固定位置)这个同学想到了旋转过程中的一个不动的点,也就是一个中心点,并且一个“绕”字表达得非常准确,我们也把她这个非常有价值的想法写下来。(板书:中心)刚才同学们从不同的视角看到或者想到了中心、方向、角度。那如果我想对指针下达一个指令,让指针从12旋转到3的位置,你会怎么下达这个指令呢?请你们试着自己研究。
活动要求:(1)先自己独立思考,再在小组内交流。(2)请试着解释你们的想法。
学生小组活动后汇报:指针绕O点顺指针旋转90毅。
师:我发觉你们都说出了中心、方向、角度。一定要这样吗?我就说绕O点旋转90毅不行吗?
生5:不行,顺时针旋转才会到3,如果是逆时针旋转就会到9了。
师:看样子,要想确保指针旋转到确定的位置,说清楚方向很重要。那为什么还要说出中心和角度呢?
生6:如果转的角度不一样,指针的位置会不一样,比如指针从12顺时针旋转30毅就到了1,顺时针旋转60毅就到了2,顺时针旋转90毅就到了3,每多一个大格就会多30毅。
师:转的角度不一样,位置也会不一样。你会观察,也会思考。现在你们能想象出指针旋转的过程吗?请先记下指针的位置和形状,然后想象指针的旋转过程。(课件演示)也就是说,说出了中心、方向、角度,旋转的结果也就确定了。中心、角度、方向在旋转中非常重要,它们就是旋转的三要素。(板书)
2.理解旋转的特征
师:借助指针,我们知道了用三要素描述旋转过程准确又完整。(出示图7)那你能完整地描述这个三角形的旋转过程吗?(指名描述)你能想象出他说的这个旋转过程吗?现在请每个同学把三角形AOB的位置和样子画在脑海里,特别提醒:中心的位置不能动,把你脑海中的三角形AOB绕O点逆时针旋转90毅。(学生闭眼想象)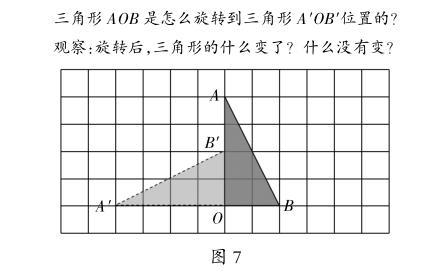
师:(课件演示)刚才你们想象的旋转过程是这样的吗?你是怎么看出三角形旋转了90毅的?
生7:OA忆和OA之间的夹角的度数是90毅。
师:你为什么要把OA忆和OA放在一起想呢?
生7:因为OA绕O点逆时针旋转90毅后会到OA忆的位置。
师:图中OA旋转到了OA忆的位置,我们就说OA忆是OA的对应线段,这两条线段之间的夹角是90毅。那像这样的对应线段你还找得出来吗?
生8:OB和OB忆也是一组对应线段,它们形成的角也是90毅。
师:请仔细观察每一组对应线段,想一想,它们有什么相同点?
生9:它们长度一样。OA和OA忆的长度是4格,OB和OB忆都是2格。
师:旋转后,对应线段的长度没有改变。还有什么也没有变?
生10:旋转后的形状没变。
生11:旋转后的大小没有变。
师:形状和大小都相同。还有吗?
生12:旋转中心的位置不变。
师:旋转后,旋转中心的位置不变,三角形AOB的形状和大小不变,所以对应点到旋转中心的距离相等。那你能找出什么变了吗?
生:图形的位置变了。图形的方向也变了。
师:从线段到图形,从图形又回到线段,我们发现,三角形AOB绕O点顺时针旋转90毅后,形状、大小不变,对应点到O点的距离相等。变化的是三角形AOB的位置和方向,具体来说就是每条边都绕O点顺时针旋转了90毅。
(三)拓展练习,丰富感知
1.停车杆的运动
师:在课前预学单中,同学们对于停车杆的运动,有的认为是旋转,有的认为是平移,现在你会怎么认为呢?
生13:我认为是旋转现象,是逆时针旋转90毅。
师:是的,这也是一种旋转现象。你能描述它的旋转过程吗?(学生描述)(出示图8)你们见过钟摆的运动吗?钟摆的运动是一种旋转现象吗?说说你的想法。
生14:钟摆的运动也是一种旋转现象,只是它摆动的角度很小。
师:尽管钟摆旋转的角度不大,但是它依然能用旋转的三要素描述旋转过程。想一想,如果继续不断地旋转下去,最终会怎么样?
生15:会形成一个圆。
师:大家能想象出一个圆吗?(课件演示线段旋转一周后形成圆的过程)你能描述这条线段的旋转过程吗?
生16:线段绕中心点顺时针旋转360毅。
师:同学们很有想象力。前面我们研究的都是一个图形绕某个点旋转,其实,在数学上,有时还可以把一个图形绕着某条线段旋转一周。如果把长方形绕着它的一条边旋转一周,你能想象出旋转后的图形吗?(学生描述,课件演示)你们太有想象力了。希望你们在以后的学习中也能插上想象的翅膀,飞得更高、更远。
三、讨论
1.要素之“要”在哪?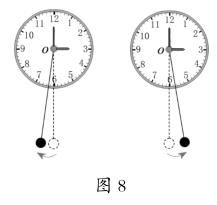
旋轉三要素的教学是第二学段旋转教学的重点。通过对学生的学前调研的分析,我们认为,要素之“要”体现在:(1)确定旋转结果的必要因素。“要让指针从12旋转到3,应该给出一个什么样的指令”,在对这个问题的思考和研究中,学生认识到要得到确定的旋转结果,旋转的三要素缺一不可。(2)判断旋转现象的重要依据。停车杆的运动、秋千的运动、钟摆的运动等都是旋转现象,我们都能够用三要素来描述运动过程。(3)研究旋转特征的重要基础。旋转变换一共有两个要点:旋转中心和角度。教学中教师多次让学生观察、体会旋转中心位置不变的特点。这些都是学生研究旋转特征的重要基础。
2.关于例2的研究与教学。
新教材在三要素的认识和画旋转图形两个教学活动中增加了例2。通过分析和思考,我们认为例2的教学是为了帮助学生在认识三要素的基础上进一步认识旋转的特征。这个探究对学生是非常有必要的。我们曾经对六年级的孩子做了一次画旋转图形的检测,在参加检测的115个学生中,全对的仅59人。从检测结果中可以发现,学生的错误集中在:方向错误,特别是逆时针方向,中心点位置移动,改变了图形的形状和大小。为此,在本课中,我们遵循从线段到图形的认知规律,借助线段研究旋转的三要素以后,再把学生的认知上升到简单的平面图形的旋转,让学生学会从复杂的图形中剥离出简单图形,经历“线段—图形—线段”的内化与循环,为画旋转图形打好基础。
3.怎么培养空间想象能力?
准确地画出旋转后的图形,要求学生具有一定的空间想象能力。要培养学生的空间想象能力,我们在教学中遵循了这样的思路:先为学生提供旋转的直观演示,让学生建立旋转的表象,在此基础上给学生提供想象的机会。在学生有了一定的想象基础后,引导学生把旋转变为他们脑海中的动态过程。有了图形在脑海中“转起来”的经验,学生对旋转的结果也就能做出准确判断。在这一过程中,教师对学生提出具体的要求,教给学生想象的方法。比如,教师特别提醒:中心的位置不能动,把你脑海中的三角形AOB绕O点逆时针旋转90毅。刻画图形—关注中心—动态旋转,清晰的三步曲让想象中的旋转过程清晰化,学生可以顺着想象的阶梯,准确地在脑海中“画”出旋转后的图形。
(执笔:钟东平、楼捷、段建国、詹婧、黄琨、徐旺、李闯)
