来宾市不动产登记数据向2000国家大地坐标系转换的方法研究及精度分析

2018-06-30梁小龙周聪林陈宣羽

企业科技与发展 2018年12期

梁小龙周聪林陈宣羽

【摘要】文章以来宾市不动产登记数据向2000国家大地坐标系转换为案例，通过对坐标转换模型选择、高等级重合点选取等方面的研究，得出适合广西地区2000国家大地坐标系转换的方法，利用现有广西高等级控制点对转换模型参数进行精度分析，并对转换后的来宾市不动产登记数据进行外业检核，结果表明，转后数据精度X方向偏差最大值为2.5 cm，Y方向偏差最大值为2.6 cm，符合转换点位平均平面位置精度优于±5 cm的要求。

【关键词】2000国家大地坐标系转换;坐标转换模型;重合点选取

【中图分类号】P226.3 【文献标识码】A 【文章編号】1674-0688（2018）12-0029-03

0 前言

随着社会的不断进步，国民经济建设、国防建设、科学研究及社会发展等方面对国家大地坐标系的应用提出了新的要求，迫切需要采用原点位于地球质量中心的坐标系统（以下简称地心坐标系）作为国家大地坐标系[1]。经国务院批准，2008年7月1日我国开始启用地心坐标系，即2000国家大地坐标系[2]。

根据国家和广西的要求，来宾市启动不动产登记数据2000国家大地坐标系转换项目。该项目的组织实施将有利于解决来宾市不动产登记数据坐标系不统一造成的成果不兼容问题，进一步提高来宾市测绘地理信息服务水平，更好地为来宾市经济建设和社会发展提供高效的测绘地理信息成果服务保障。

1 工作准备及技术路线

1.1 工作内容

（1）来宾市不动产登记数据及相关矢量数据坐标转换，从原始的1980西安坐标系转为2000国家大地坐标系。

（2）转换数据精度符合相关要求。

1.2 主要精度指标

参照《现有测绘成果转换到2000国家大地坐标系技术指南》中对2000国家大地坐标系坐标转换提出的技术要求，结合来宾市不动产登记数据成果现状，对项目转换精度提出如下要求。

（1）控制点成果转换。选择未参与转换参数计算部分重合点作为外部检核点：用转换参数计算至少6个重合点的转换坐标与已知坐标进行比较，同时进行外部检核[3]。控制点平面转换精度满足以下指标：模型计算内符合精度优于±3 cm，模型计算外符合精度优于±5 cm。

（2）不动产登记数据转换：来宾市不动产登记数据采用1980西安坐标系，转换至2000国家大地坐标系后，转换点位的平均平面位置精度需优于±5 cm。

1.3 技术路线

坐标转换技术路线如图1所示。

2 坐标转换模型的选择

2.1 二维平面坐标转换模型

二维平面坐标转换模型分为二维四参数转换模型及二维七参数转换模型。

2.1.1 二维四参数转换模型

二维四参数转换模型[4]公式如式（1）所示。

x2y2=x0y0+（1+m）cosα -sinαsinα cosαx1y1（1）

式中：x0、y0为平移参数，α为旋转参数，m为尺度参数，x2、y2为目标坐标系下平面直角坐标，x1、y1为原坐标系下平面直角坐标。

2.1.2 二维七参数转换模型

二维七参数转换模型[4]公式如式（2）所示。

式中：△B、△L为经纬度差值（单位为弧度），△a、△f为椭球长半轴（单位为m）、扁率差，εX、εY、εZ为旋转参数（单位为弧度），△X、△Y、△Z为3个平移参数（单位为m），m为尺度参数。

2.2 三维空间坐标转换模型

常用的三维空间转换模型有布尔沙模型、莫洛金斯基模型等。

2.2.1 布尔沙模型

Bursa七参数坐标转换模型[5]公式如式（3）所示。

XTYTZT=△X△Y△Z+ 0 -ZS YS ZS 0 -XS-YS XS 0εXεYεZ+mXSYSZS+XSYSZST（3）

式中有3个平移参数[△X △Y △Z]T，3个旋转参数[εX εY εZ]T和1个尺度参数m。

对相似变换后的重合点残差VX、VY、VZ采用多项式拟合。

式中：B、L单位为弧度;k为拟合阶数，aij为系数（通过最小二乘求解）。

2.2.2 莫洛金斯基模型

莫洛金斯基模型[5]公式如式（4）所示。

式中：[X1 Y1 Z1]T为01-X1Y1Z1下的坐标，[X2 Y2 Z2]T为02-X2Y2Z2下的坐标，[X' Y' Z ']T为旋转中心坐标，△x、△y、△z为平移参数，εX、εY、εZ为旋转参数，k为尺度参数。

通过相关系数的对比分析，莫洛金斯基模型的稳定性优于布尔沙模型，由于莫洛金斯基模型参数之间不相关，坐标发生微量变化对莫洛金斯基模型七参数影响不大，故小范围坐标转换可以考虑使用莫洛金斯基模型[5]。

由于广西壮族自治区行政区域面积比较大，横跨经度较广，且采用二维转换模式受投影变形的影响较大，故宜采用布尔沙七参数转换模型进行坐标转换。

3 重合点选取与精度分析

3.1 重合点选取

由于国家三角点一般都是20世纪布测的，我国地壳运动变化复杂，点位变化也复杂，成果精度低，这样控制点的转换会受到大地形变的影响，如果利用这些有局部变形点作为重合点求取转换参数，就会降低转换参数精度，从而影响坐标转换的精度。因此，在求解转换参数时，应对参与求解转换参数的重合点进行认真地分析、筛选、试算，剔除局部变形点;采用不含粗差、分布均匀且包含转换区域的重合点进行转换参数计算[3]。

经过反复试算分析，在本项目坐标转换过程中将广西现有的高精度A、B级GPS控制点作为七参数转换模型重合点和检核点参与计算。计算步骤如下：{1}初始重合点的选取按35、36、37度带分带进行，选取初始重合点。{2}确定参数计算模型（布尔沙模型）。{3}导入重合点，计算残差和中误差，剔除残差大于3倍中误差的初始重合点再次计算，直至选出合格的重合点分别计算35、36、37度带的布尔沙坐标转换模型七参数。

来宾市兴宾区地处广西中部，属36度带，所选重合点均为剔除残差大于3倍中误差的重合点，最终重合点选取分布图如图2所示。

3.2 精度分析

3.2.1 内符合精度分析

在七参数转换模型计算过程中，利用重合点转换前后获得的2000国家大地坐标系成果计算模型内符合精度平面点位中误差小于0.001 m。

3.2.2 外符合精度分析

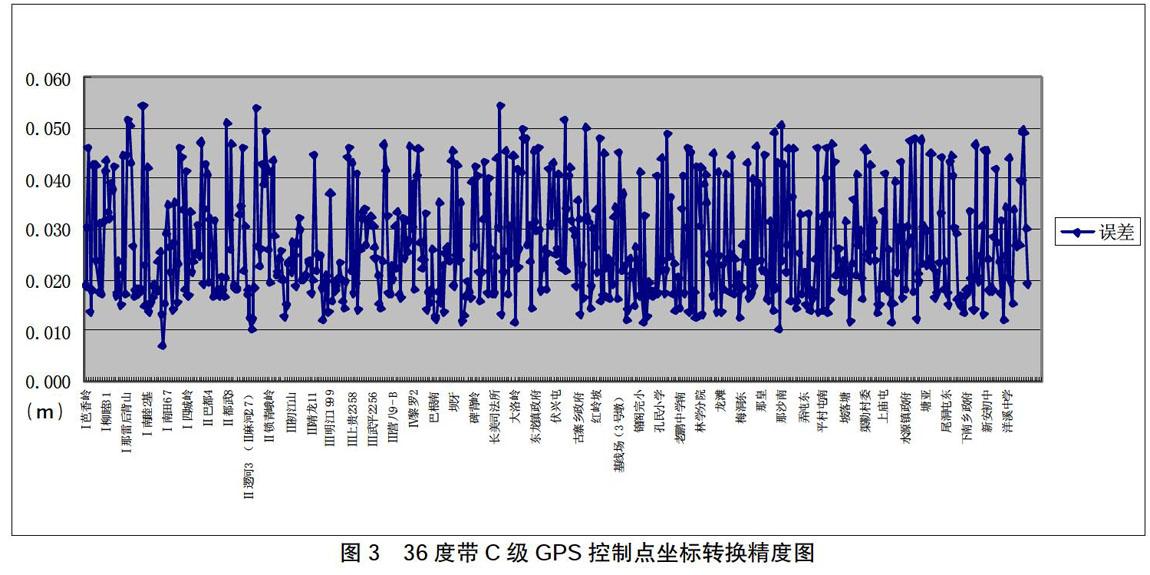
采用36带范围的其他C级GPS控制点分别对七参数转换模型进行外符合精度检核分析。C级GPS控制点所选择的部分检核点平面点位精度分布如图3所示。

其横坐标为检核点的点名，纵坐标为对应点的平面检核精度。所有检核点坐标转换的平均精度为0.027 m，最大为0.055 m，最小为0.007 m。

4 外业核查

为了评估转换参数和转换成果的外符合精度，在作业区范围布设控制点并进行外业碎部点检核，确保成果精度。

在作业区范围均匀布设4组控制点，每组2个控制点，互相通视。在8个控制点上进行静态观测2小时，观测数据与邻近GXCORS系统基准站的同步观测数据组成GNSS控制网，使用天宝解算软件TBC进行基线处理，COSA软件进行平差，求得的控制点点位精度满足国标E级控制点的精度要求，用于外业碎部点检核。

在每组控制点上架设全站仪，定向后测量明显的不动产登记数据碎部点，记录碎步点测量成果，与内业不动产数据同点位坐标比较，形成外业检核精度表。

经整理较差结果形成如图4所示的外业核查精度图。从图4可看出50个外业核查点的X方向偏差最大值为2.5 cm，Y方向偏差最大值为2.6 cm，转换点位的平均平面位置精度优于±5 cm。