基于竞争与协同效应的复杂制造任务一对多双边匹配模型
2018-06-30任明仑
任 磊,任明仑
(合肥工业大学 教育部过程优化与智能决策重点实验室,安徽 合肥 230009)
0 引言
互联网时代,以智能互联产品为代表的制造任务呈现出功能多样化、个性化和复杂化的特征,资源有限的企业难以独立承担,需要多学科、跨组织、跨区域的多主体协同设计与制造[1]。以社会信息物理系统(Social Cyber-Physical System, SCPS)、大数据和云制造技术为基础,以大规模协同合作、全面感知、实时决策、社会化资源的共享与利用为目标的智慧云制造,为制造主体把握市场机遇、实现复杂制造提供了平台支撑[2-3]。一方面,不同主体(制造企业、客户、供应商甚至网络上的业余设计人员等)将自身闲置的分散、多层次制造资源和能力以服务封装的形式在云平台进行共享和社会化,实现分散资源的集中共享;另一方面,企业以按需、实时的方式在云平台上发现和组织合适粒度的服务,构建基于任务驱动的服务单元联盟,实现集中资源的分散使用。云平台中心不仅为任务方、服务方提供注册和质量评估机制,还为其协商谈判、市场竞拍和自由交易提供了场所,通过双边匹配机制实现云系统中供需的合理匹配和资源的优化调度。现有任务分配只是从任务方约束的角度进行单向匹配,注重服务功能、业务能力、信任、信誉等匹配指标和评估算法,将最好的服务推荐给任务方[4-6],虽然提升了用户满意度,却忽略了服务方的自主性要求,形成“错配婚姻”现象,不仅造成云资源的低效利用,更伤害了成员的竞争积极性,从而影响系统的稳定性和长期发展。实际上,服务单元拥有自己的战略远景和目标市场,能够根据能力和特长为某一类或几类客户提供优质服务[7],并对任务方提出相应的资格审查和评选指标,如请求真实性、信誉、付款速度、工艺要求等,避免机会主义、搭便车等带来的较大风险。云平台制造任务的分配是一个典型的多指标双边匹配问题,需要综合考虑任务方的利益诉求和服务方的市场定位,实现双方期望效用最大的满意匹配。
双边匹配决策是指依据匹配双方的相互评价信息,通过最大化双方的满意度来实现有效匹配的过程[8-9]。Gale等[10]分析了婚姻匹配和大学录取问题,最早提出双边匹配模型,随后双边匹配决策方法被逐渐应用到电子商务交易、人力资源、知识服务、制造等领域[11-12];Haas等[13]应用双边匹配模型重新界定了基于偏好的社会化云计算资源分配问题,并运用启发式算法获取稳定、公平的满意匹配方案;Xu等[14]面向云计算服务,构建了基于稳定匹配框架的名为Anchor的一般资源管理系统架构,运用一对多双边匹配解决虚拟机和物理服务器的映射问题;匡桂娟等[15]基于婚姻匹配方法对云计算任务进行分配建模,运用图匹配理论构建了面向任务、资源双方偏好满意度最优的一对一匹配模型;Cheng等[16]针对制造系统中的双边匹配问题,构建了服务供应与需求的匹配超网络模型,但其主要从功能语义的角度进行双向匹配,忽视了双方服务质量的约束;赵金辉等[17]针对云制造中存在的虚假信息、不确定性和机会主义等问题,提出基于服务质量的制造服务一对一双边匹配模型,对比了单向与双向匹配方法的优劣。目前,双边匹配研究假设匹配主体相互独立,所给出的评估偏好和决策行为不受其他成员的影响。然而现实中,匹配主体总是处于一定的圈子或社会网络中,具有竞争冲突、合作、朋友等社会关系的其他成员的决策会影响匹配主体的价值判断和满意度。制造任务方存在市场、资源的竞争关系[18],其满意度不仅来源于服务方,还来源于竞争对手获得的服务方案,特别是当两个任务方均希望获得某一重要服务时,一方获取服务将导致令一方因失败而离开云平台。同样,云服务基于业务、社会因素等交互形成多种社会关系,如资源共享、交易合作、社会相似等[19],关系紧密的近邻服务通过相互间的资源、信息和知识等协同影响该服务单元的决策行为和偏好。服务获得的效用和满意度来源于任务方和匹配在一起的合作伙伴,两个经常合作的服务单元更倾向于参与到同一个项目中,因为如果分别参与到不同项目中,则可能会降低获得的效用。因此,在制造双边匹配中考虑匹配主体间的网络关系和竞争协同效应,将获得更符合实际情形的、稳定满意的匹配结果。
虽然制造领域还未将社会关系和协同效应应用到双边匹配过程中,但是在医院医生匹配、大学招生、学生宿舍分配、企业联盟形成等问题中,已经有大量学者将外部性效应即互补性、同群效应(Peer effect)考虑到双边匹配模型中,认为夫妻、朋友等社会关系是制约匹配主体决策行为和结果偏好的关键因素[20]。Bodinebaron等[21]构建了加权朋友网络,分析了同群效应对大学宿舍匹配中学生获得效用的影响,提出基于社会福利最大的配对稳定匹配模型;Mumcu等[22]研究了公司职员个人偏好依赖于社会外部性,特别是朋友、熟悉关系的情况,给出了基于外部性效应的一对一匹配存在稳定匹配对的充分条件和算法;Nguyen等[23]针对国家居民匹配计划中的医生匹配问题,分析了互补性和夫妻关系对匹配模型稳定性的影响,证明了近似可行稳定匹配的存在; Bando针对劳动力市场中的匹配问题,认为公司的偏好不仅依赖于其雇佣的员工,还受其竞争对手所雇佣员工的影响,给出了弱稳定匹配存在的条件[24],并进一步分析了竞争对手雇用员工对公司效应的影响矩阵,给出了竞争环境下的双边匹配问题描述,提出可接受的延期搜索算法获取最优解,但没有给出具体的公司竞争关系网络和竞争效应的表示[25]。以上研究分析了外部性对双边匹配稳定性的影响,但其应用场景均为匹配主体的一方存在同群效应、互补性关系,没有考虑匹配双方同时存在外部性的情形,特别是制造领域中任务方的竞争关系和服务方的协同效应。上述成果虽然给出了外部性的界定,运用互评信息得到成员间的满意度,但是没有构建成员的社会关系网络,得到的信息较为主观,难以反映成员间的相互影响。而云平台上的任务以及服务双方的关系更加复杂,其他领域基于外部性的匹配方法难以直接应用于制造领域。
智慧制造环境下,平台上的任务方为了占领产品市场、争夺稀缺资源而存在激烈的竞争,竞争对手的决策偏好和行为策略影响其方案的制定,任务相互之间的满意度受竞争关系强度和与竞争对手满意度偏差的影响,也应将其考虑到匹配过程中。同时,服务单元具有异质性、社会性、协同性,通过多种社会关系形成面向资源、信息、知识的协同效应,影响服务方的行为偏好和获取的价值效用。云平台的任务匹配不仅考虑服务单元、任务方的满意度,还应考虑基于竞争关联的任务间满意度和基于协同效应的服务间满意度,以提升任务的完成效率和平台社会化福利水平。因此,根据实际制造过程特征,本文构建任务竞争关系网络和服务协同网络模型,提出了基于竞争与协同效应的任务—服务一对多双边匹配问题,以决策主体的期望值或市场定位为参照点,并提出基于期望效用理论的双方满意度聚合方法;针对任务方竞争关系、服务社会关系对匹配结果的影响,提出基于竞争关联的任务间满意度和基于协同效应的服务间满意度计算方法;以任务满意度、服务满意度、任务间满意度和服务间协同满意度最大化为目标,提出基于竞争与协同的一对多双边匹配多目标优化模型。运用改进非支配粒子群优化(Particle Swarm Optimization,PSO)算法对模型进行求解,获得多个Pareto最优解,再基于加权理想解相似度顺序偏好法(Technique for Order Preference by Similarity to Ideal Solution,TOPSIS)评估获取最佳匹配方案,满足客户的个性化需求和实际制造场景的约束。
1 问题描述
复杂制造任务要求运用多种资源和工艺知识,一般需要多个服务单元协作以服务组的形式完成,例如谷歌智能汽车项目需要谷歌智能系统、宝马制造部门、奔驰组装等多个公司或部门协同。因此,云平台的任务分配是一个一对多双边匹配问题。同时,匹配主体间的竞争、协作等社会关系影响彼此的决策行为和效用获取,双边匹配满意度模型还应增加任务间满意度和服务间满意度。在复杂任务情境下,本文分析了任务竞争网络和服务协同网络,主要关注基于竞争与协同效应的一对多匹配问题,从而形成满足真实情形的满意稳定匹配。
1.1 一对多双边匹配
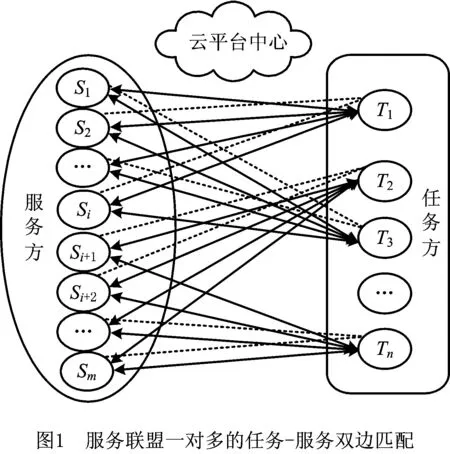
云平台中共拥有n个制造订单请求,即任务方T=(T1,T2,…,Tm),Tj为第j个任务方,j=1,2,…,n;同时,平台上存在m个服务方S=(S1,S2,…,Sm),Si为第i个服务提供者,i=1,2,…,m。如图2所示,每个服务Si拥有多个资源,能够完成相应的制造任务。服务每次最多参与到一个任务Tj中,每个任务Tj需要λ个服务,λ值由任务方规定。本文假定λ≥2即为一对多匹配,最终一个任务由包含λ个服务的服务组Gj完成。给定T对S的满意度评价指标为A=(A1,A2,…,Ao),Ak为第k个评价属性,wA=(wA1,wA1,…,wAo)为指标A的权重;服务方S对任务T的满意度评价指标为B=(B1,B2,…,Br),Bl为第l个评价属性,wB=(wB1,wB1,…,wBr)为指标A的权重;Tj对S的每个指标的期望值构成期望矩阵Qj=(qj1,qj2,…,qjo),其中qjo为任务Tj对服务在第o个指标上的期望值,则所有T的期望矩阵为QT=(Q1,Q2,…,Qn)。相应地,Si对T的每个指标的期望值构成期望矩阵,即其市场定位为Pi=(pi1,pi2,…,pir),其中pir为Si在第r个指标上的市场定位,则所有S的期望矩阵为PS=(P1,P2,…,Pm),从而得到一个双方满意度最大的稳定匹配μ:S∪T→S∪T。
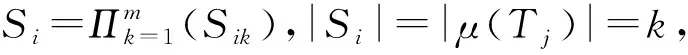
定义2一对多匹配μ:S∪T→S∪T中,若匹配对(Si,Tj)满足以下条件:①∃Si,Sl∈S,Tj,Tk∈T,Si∈μ(Tj),Sl∈μ(Tk),满足αij<αik且βij<βlj,α,β分别为服务满意度和任务满意度;②∃Si∈S,Tj,Tk∈T,Si∈μ(Tk),Tj∈μ(Tj),满足αij<αik;③∃Si,Sl∈S,Tj∈T,Tj∈μ(Si),Si=μ(Si),满足βij<βlj;④∃Si∈S,Tj∈T,Si∈μ(Si),Tj∈μ(Tj)。则称(Si,Tj)为阻碍稳定对。如果不存在稳定对,则μ为稳定匹配。
图1中的S1,S2,Sm和任务方中T1,T2,Tn的有向细线的权值表示S和T的双方满意度水平,Si和Tj间的无向虚线表示两者为稳定匹配对。由m条无向粗线连接形成的匹配主体对集合μt,Tn-1在μ中为单身。
1.2 基于竞争与协同效应的一对多双边匹配问题
云平台中的任务间基于市场和资源争夺形成竞争关系,服务之间基于社会交互和协作行为形成多种社会关系数据,通过聚合关系强度衡量任务间的竞争关系和服务间的协同效应,形成任务竞争网络和加权服务协同网络。网络中任务间的竞争关系影响任务方的决策行为,服务单元通过正向协同关系影响彼此的匹配决策偏好。因此,在任务关系网络和服务协同网络构建的基础上,提出基于竞争与协同效应的一对多双边匹配问题。
(1)任务竞争关系网络与服务加权协同网络
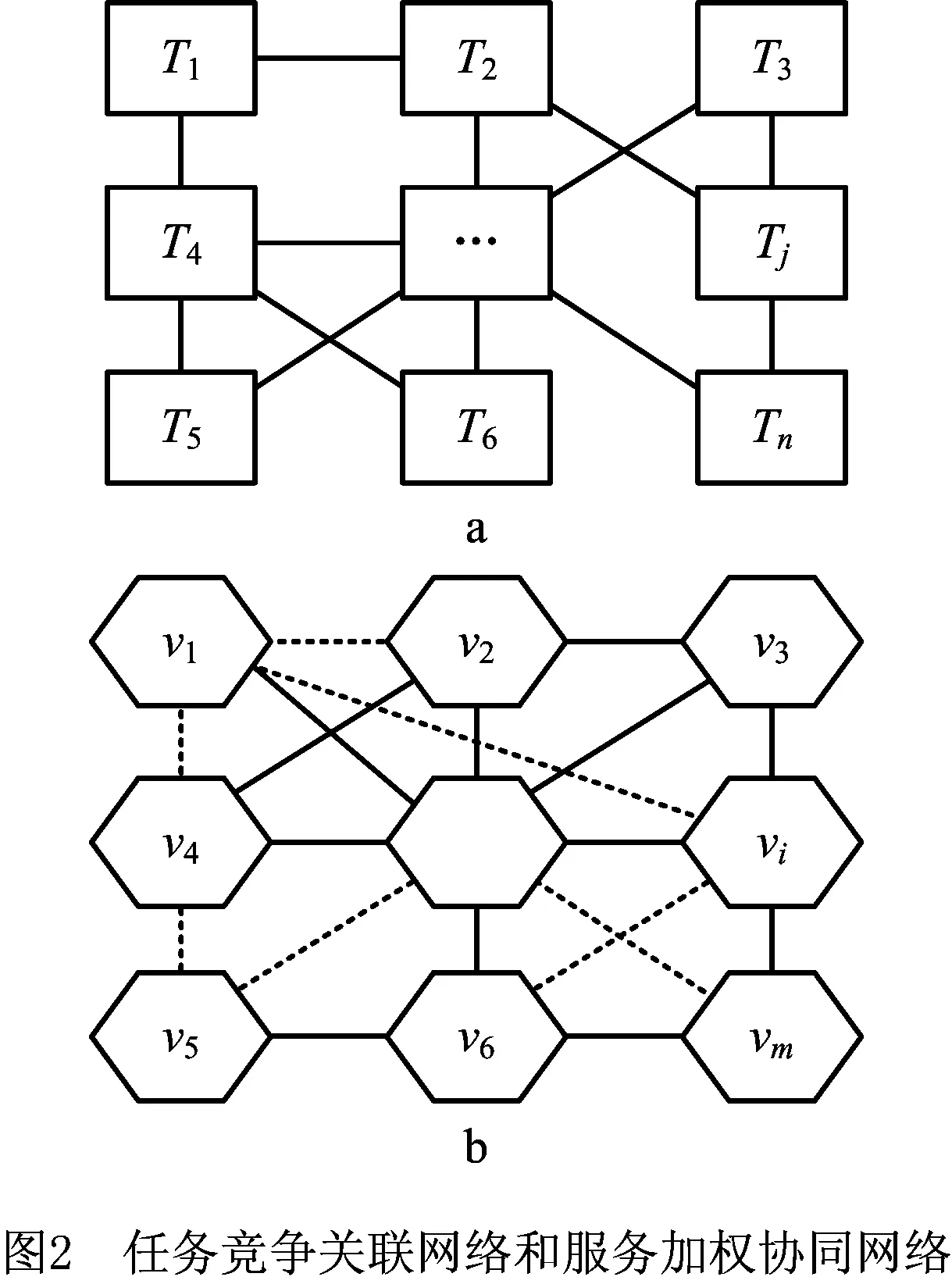
定义3任务竞争关系网络是任务方为了争夺共同的市场客户和优质稀缺资源而形成的竞争关系所交织成的多维复杂网络,以任务为节点、竞争关系为边,描述为任务竞争关系网络图GCP=(U,QoT,E,w),如图2a所示。其中:U=(u1,u2,…,un)为任务方节点集;QoT为任务方的评估值集;E=(E1,E2,…,Em)为边集即竞争关系集;w=(w1,w2,…,wm)为边权值集,即竞争关系强度值集。竞争关系SRC包括市场和资源竞争关系,当Ti和Tj均同时向细分市场Mk提供产品服务,即Ti→Mk,Tj→Mk时,两任务存在市场竞争关系SRMC(i,j);当Ti和Tj均同时投资使用资源Pk,即Ti→Pk,Tj→Pk时,两任务存在资源竞争关系SRRC(i,j)。
定义4共同关注服务是任务方与其竞争对手均想匹配到的、评估值最高的重要服务单元C-ES,C-ES可能是一个服务也可能为多个服务。当|C-ES|=1时,任务方获取共同关注服务,其竞争对手因满意度最低而直接离开匹配市场,反之亦然。云平台将C-ES分配给其他任务方,以避免出现竞争双方由于内部策略、嫉妒心态等而出现的任务方匹配失败现象。当|C-ES|≥2时,任务方与其竞争对手平等地获取均等的C-ES,实现心态平和的公平匹配。
此外,基于决策主体的比较心理和对损失受益的态度,竞争关系的存在使得任务方非常关注竞争对手匹配结果的满意度,如果自己与竞争对手的满意度差值较大,即使自身满意度较高仍会感知到挫败感和不满意,从而导致匹配方案不稳定。竞争关系越强,因满意度差值所产生的不满意越强。因此,将基于竞争关系强度和满意度差的聚合值看作任务间的满意度增加到双边匹配中,能够提升匹配方案的稳定性。
定义5服务加权协同网络是服务单元间通过多种社会关系进行资源、信息、知识的传递和交互而形成的多维复杂网络,以服务为节点、协同关系为边构成协同网络图GWSN=(V,QoS,L,ζ),如图2b所示。其中:V=(v1,v2,…,vm)为服务节点集;QoS为服务质量值集;L=(L1,L2,…,Ln)为边集,即协同关系集;ζ=(ζ1,ζ2,…,ζn)为边权值集,即服务对协同效应值集。
本文重点关注服务间的交易合作、资源共享、社会相似3类协同关系:当服务Si和Sj均参与到共同任务Tk,即Si→Tk,Sj→Tk时,两服务存在交互合作关系SRIT(i,j);当Si具有资源集合Ri,Sj的资源集合为Rj,Ri∩Rj为两个服务的互补性资源数且不等于零,共享资源数Rs≠0时,服务具有资源相关关系SRRR(i,j);当服务Si和Sj在属性集Ak上具有相同或相似的数值时,两服务存在社会相似关系SRSim(i,j)。服务单元的决策行为受到与其有社会关系的邻近服务行为的影响,需考虑其对合作伙伴的满意情况,本文将协同效应看作服务间满意度应用到双边匹配中,提升了匹配结果的稳定性。
(2)基于竞争与协同效应的一对多双边匹配问题
双边匹配的目标是尽量使协同效应、合作绩效高的服务单元匹配到同一任务中,为存在竞争关系的任务分配均等的、差值较小的服务方案。文中以任务满意度、任务间满意度、服务满意度和服务间满意度最大化为目标,构造基于竞争与协同效应的一对多双边匹配问题。
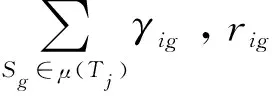
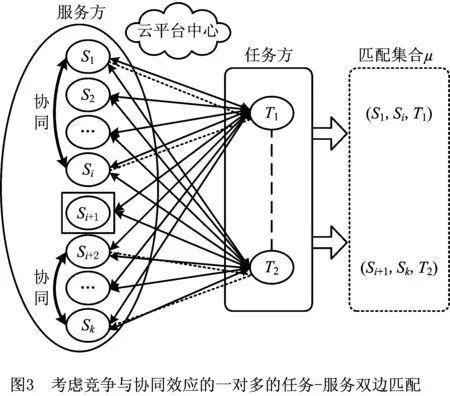
图3中形成的稳定匹配为(S1,Si,T1)和(Si+2,Sk,T2),其中:S1,S2,Sk和任务方中T1,T2的有向细线的权值表示双方的满意度水平,S1和T1间的无向虚线为稳定匹配对;S1和Si间的有向粗线表示服务组内的协同满意度,T1和T2间的有向虚线表示两任务间的满意度;矩形中的Si+1为T1,T2共同关注的服务,Si+1唯一,不能分配给两者中的任意一个,以避免因竞争而匹配失败。(S1,Si,T1),(Si+2,Sk,T2)是最优的满意稳定匹配方案。
2 基于竞争与协同的双向任务匹配多目标决策模型
联盟中心通过大量交易信息统计计算得到任务方和服务方的评估值。给定任务的参数约束和期望值、任务竞争关系、服务市场定位及服务社会网络,通过期望效用理论聚合服务满意度α和任务满意度β,给出任务间满意度σ和服务间协同满意度θ的计算方法,建立以四者满意度最大化的多目标匹配模型,获取稳定性的满意匹配方案。
2.1 基于期望效用的双方满意度聚合方法
云平台通过收集任务方和服务方的注册信息以及交易和交互沟通数据,对匹配双方给出客观、科学的评价。给出服务评估值QoS=(qos1,qos2,…,qosm),qosi为第i个服务的评估值,qosi=(ai1,ai2,…,aio),aih为第i个服务在第h个指标上的数值,服务评估指标包括时间、成本、可靠性、信誉、产品质量;同样,任务评估值QoT=(qot1,qot2,…,qotn),qotj为第j个任务的评估值,qotj=(bj1,bj2,…,bjr),bjh为第j个任务在第h个指标上的数值,任务评估指标包括缴款速度、市场信誉、可靠性等;任务方的服务期望值为EES=(es1,es2,…,esn),esj为第j个任务的期望esj=(eaj1,eaj2,…,eajo),eajh为第j个任务在第h个指标的期望值;服务方市场定位EET=(et1,et2,…,etm),eti为第i个服务的定位esi=(eti1,eti2,…,etir),etih为第i个服务在第h个指标的期望值。

式中:xij为决策变量,xij=1表示第i个服务匹配给第j个任务;αij为Si对Tj的服务满意度。同样,可以得到任务Tj对服务Si的期望值EUji和整个匹配方案的任务满意度β,
2.2 基于竞争关联的任务间满意度计算
任务方之间存市场竞争和资源竞争两类关系。当共同关注的服务不均等地分配给任务方和竞争对手时,未获得重要服务一方的满意度为零,即退出匹配。当共同关注的服务均等地分配给双方时,通过竞争关联强度与满意度差值来聚合任务间满意度,竞争强度对满意差值具有放大作用,竞争关系强度越大,基于差值的任务间满意度越小。不具有竞争关系的任务间满意度只要计算相互的满意度差值,然后加权得到整个方案的任务间满意度。
(1)竞争强度的计算
1)市场竞争强度 当两任务方均为某一细分市场或客户提供相同的产品服务时,两者存在市场竞争。面对不同的竞争对手,感受的竞争强度不同,这里以市场共同度来衡量市场竞争关系强度。市场共同度MCP(j,k)为任务方Tj和竞争对手Tk共享细分市场的程度,
(3)
式中:pjy为任务方Tj在细分市场y的产品销售值,pj为任务方Tj在所有市场的产品销售值,pky为对手Tk在细分市场y的产品销售值,pk为对手Tk在所有市场的产品销售值。MCP(j,k)为对手Tk在所有细分市场的产品对任务方Tj带来的竞争压力。
2)资源竞争强度 当两任务方均为争夺、抢占某一优质资源提供大量投资时,两者存在资源竞争。以资源投资共同度来衡量资源竞争关系强度RCP(j,k),
(4)
式中:qjy为任务方Tj在资源y上的投资份额,qj为任务方Tj在所有重要资源的投资值,qky为对手Tk在资源y上的投资值,qk为对手Tk在所有重要资源的投资值。RCP(j,k)为对手Tk在所有重要资源的投资值对任务方Tj带来的竞争压力。
任务间的竞争关联强度表示为CP,聚合任务节点j,k间的竞争关系强度
CP(j,k)=w1MCP+w2RCP。
(5)
式中w1,w2为市场、资源竞争关系的权重。当CP(j,k)=0时,任务节点j与k不存在竞争关系;当CP(j,k)=1时,任务节点j与k间的竞争关联强度最大。
(2)任务间满意度的计算
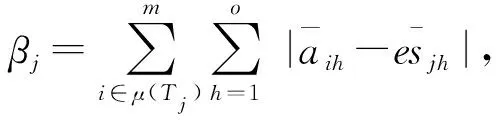
Δ(j,k)=
(6)
通过竞争关联强度进一步放大Δ(j,k),得到基于竞争关联的满意度差值
(7)
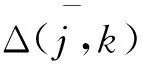
2.3 基于社会网络的服务协同满意度计算
服务间有多种社会关系,如资源共享、交易合作、社会相似关系等。文中运用服务社会关系强度来度量两个服务间的协同效应(即协同满意度),进一步加权得到服务组内的服务间协同满意度。
(1)服务对协同效应的计算
1)交易合作关系强度(SRIT) 当多个服务同时协作参与到同一个云任务或项目中时产生交易合作关系,采用所有时期的交互量TA和当前合作活跃度CA衡量SRIT的强度:
QSIT(i,j)=w1TA+w2CA=
(8)
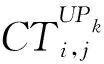
2)资源共享关系强度(SRRR) 服务拥有信息、设备、知识、软件等多种资源,采用过聚合资源共享水平RSi,j和互补水平RCi,j得到SRRR的关系强度:
QSRR(i,j)=w1RSi,j+w2RCi,j;
(9)
(10)
式中:tp(i,j)表示共享资源类型,am(i,j)表示每一类的资源共享数量;Ndifferent(i,j)表示服务Si和Sj具有不同类型资源的数量,Nall(i,j)为所有资源类型的数量。
3)社会相似关系强度 具有相似的社会属性和运行环境的服务间形成社会相似关系,通过聚合服务流行度SP、合作伙伴个数CP、信誉R和所有者O度量SRSim(i,j)的关系强度:
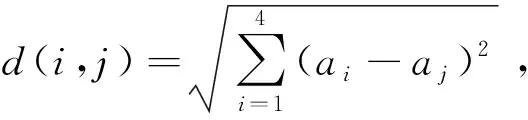
通过加权聚合服务节点i和j间的3种社会关系强度,可以得到服务单元间的协同效应QS(i,j),
QS(i,j)=ω1QSIT+ω2QSRR+ω3QSSim。
(12)
式中ω1,ω2,ω3分别为3类关系的权重。当QS(i,j)=0时,服务节点i与j不存在协同效应;当QS(i,j)=1时,服务节点i与j间的协同效应最大。
(2)服务协同满意度的计算
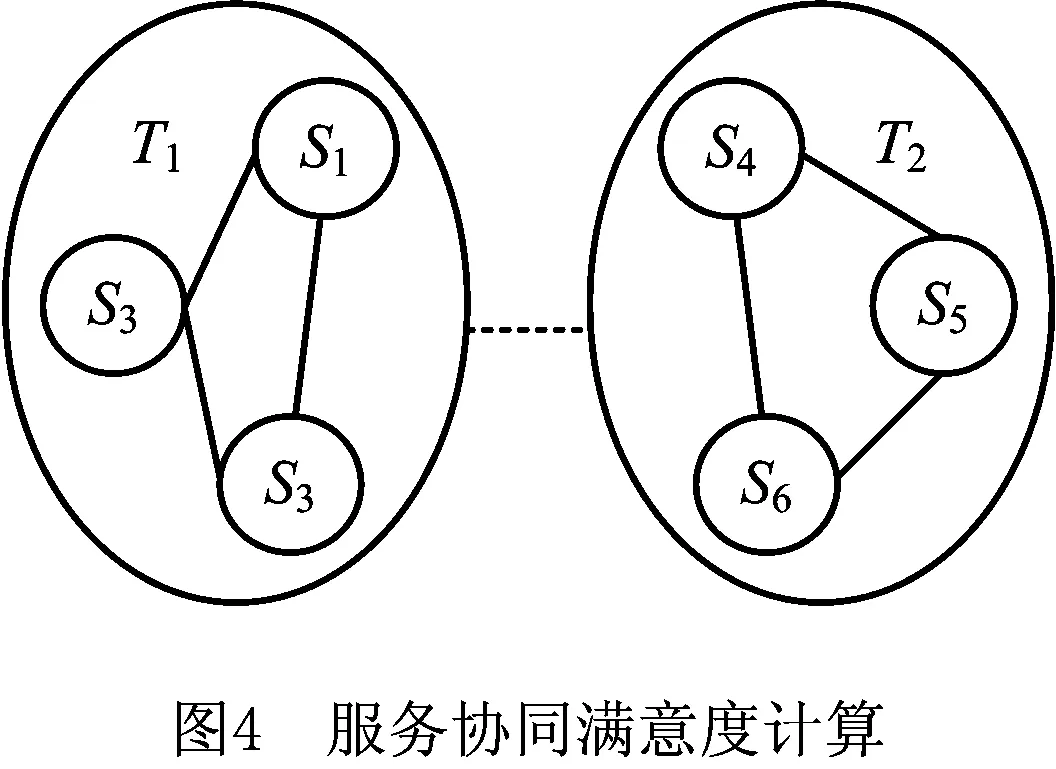
复杂任务需要多个服务单元完成,服务方案中服务协同满意度是服务组内所有服务间满意度的加权相加。如图4所示,服务组1(S1,S2,S3)完成任务T1,服务组2(S4,S5,S6)完成任务T2,则整体协同满意度包括了组1的服务间满意度和组2的服务间满意度。服务间满意度等于协同效应,即γig=qsig,且γig=γgi,从而获取所有服务间的协同满意度矩阵γ=(γig|i≠g,i=1,2,…,m,g=1,2,…,m)。直接将组内服务间协同满意度相加聚合得到任务Tj所匹配服务组Gj=μ(Tj)的满意度:
(13)
聚合匹配方案中所有服务组内服务协同满意度,得到整体方案的服务间满意度
(14)
式中:xij为决策变量,xij=1表示第i服务匹配给第j个任务;γig为在服务组Gj=μ(Tj)中服务Si对Sg的满意度;μ(Tj)为匹配给任务Tj的服务组,包括多个服务单元。
2.4 基于竞争与协同的任务双边匹配多目标优化模型
依据上文得到的服务方对任务方的满意度α、任务方对服务的满意度β、任务间的满意度σ和服务单元间的协同满意度θ,构建最大化四者满意度的多目标任务匹配数学模型:
F=(Z1,Z2,Z3,Z4);
(15)
(16)
s.t.
(17)
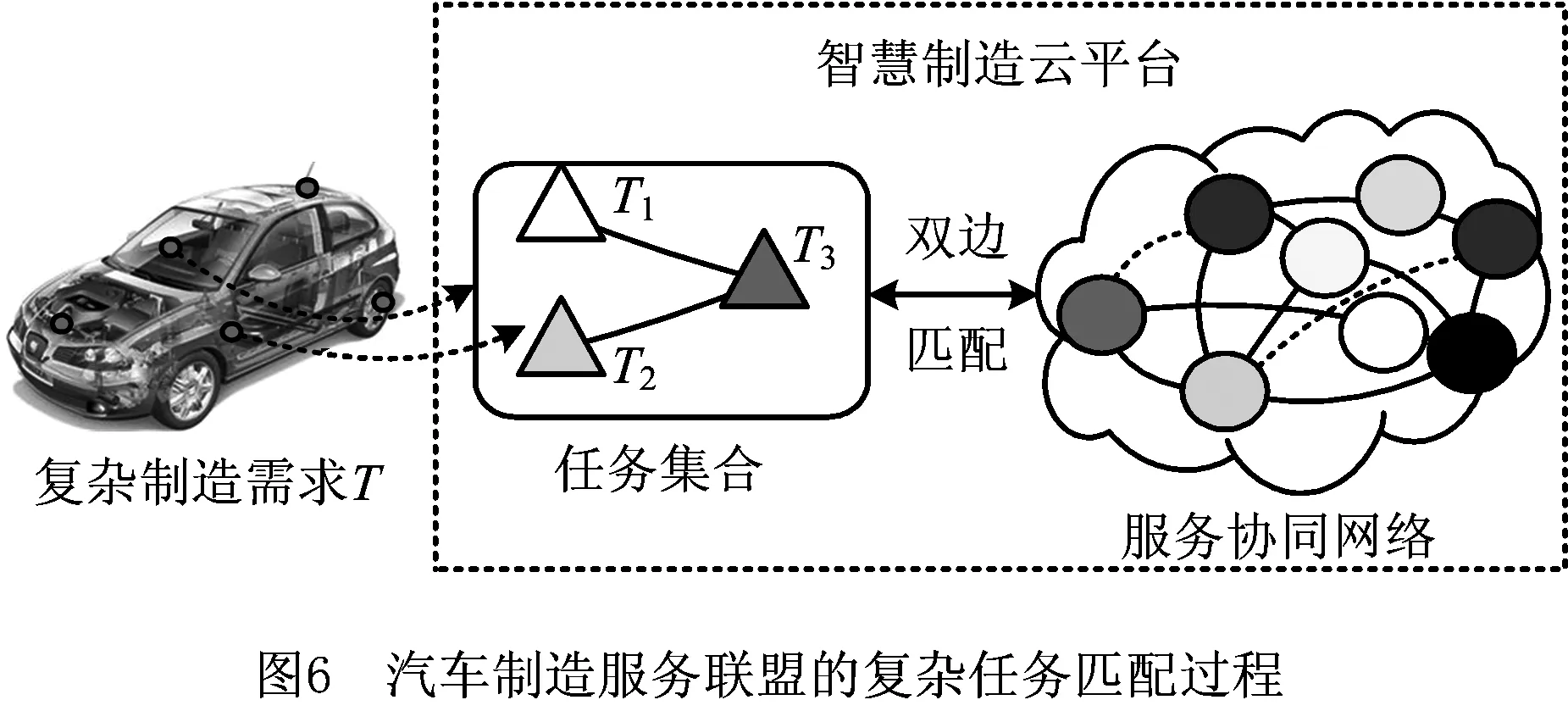
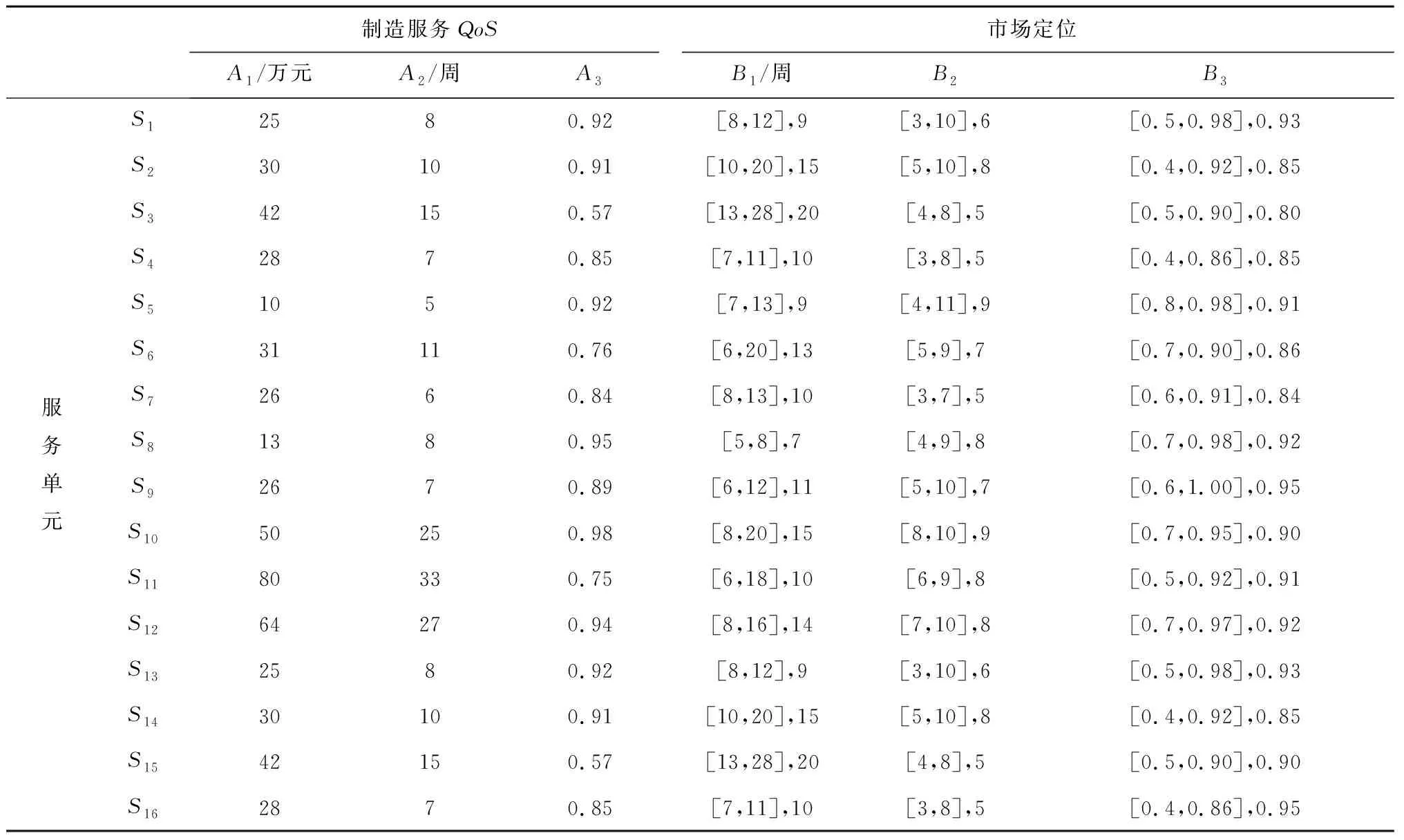
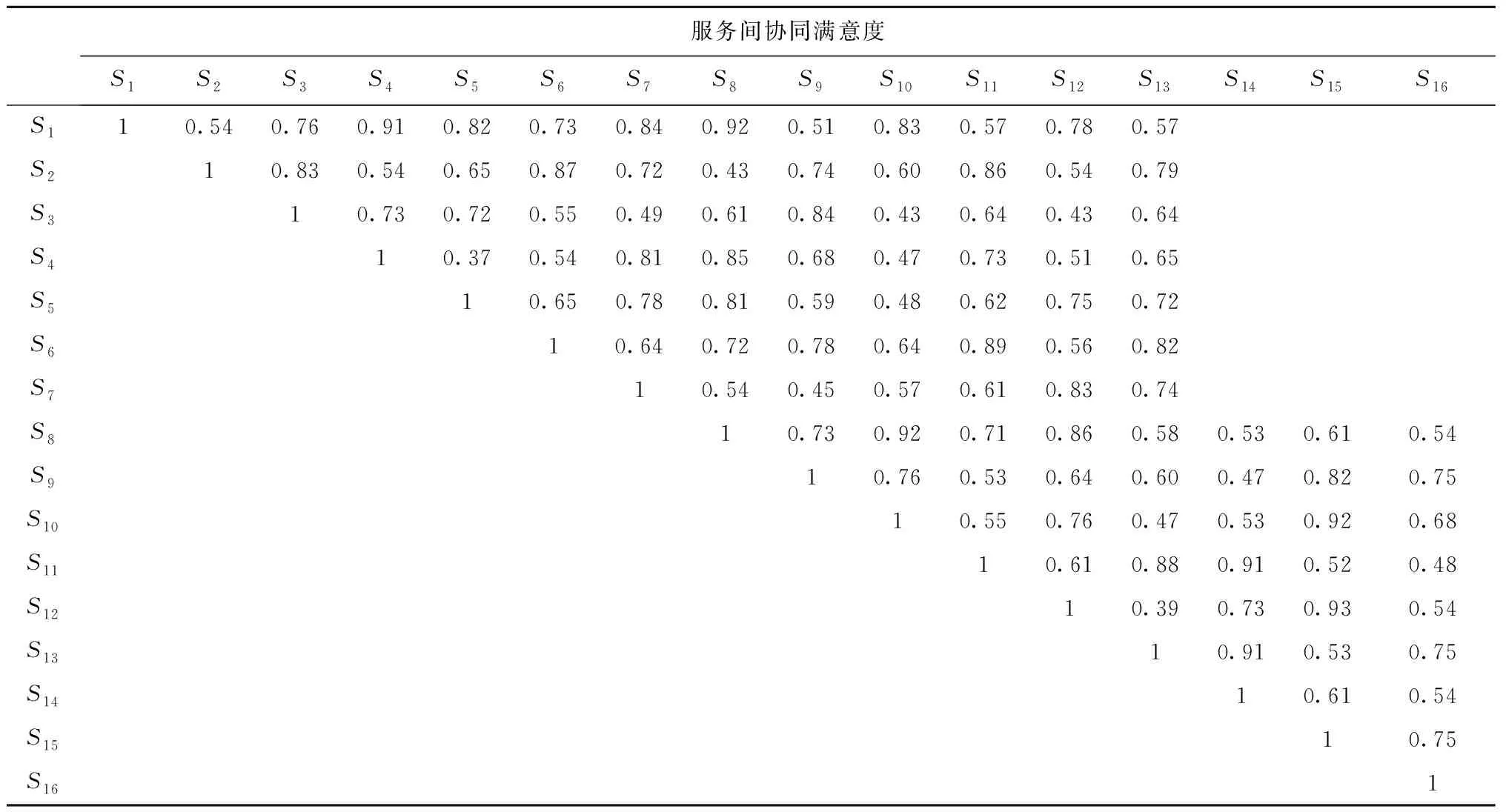
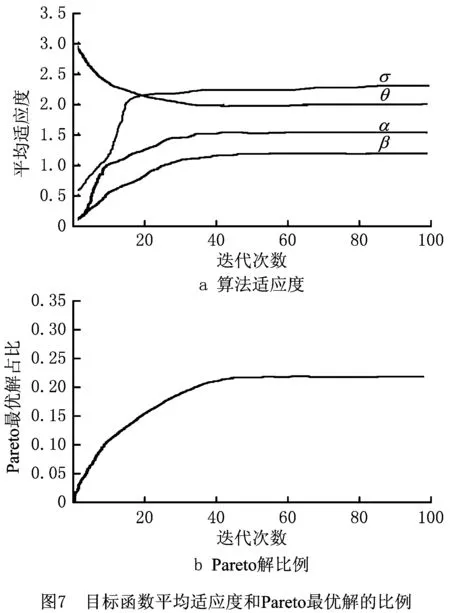
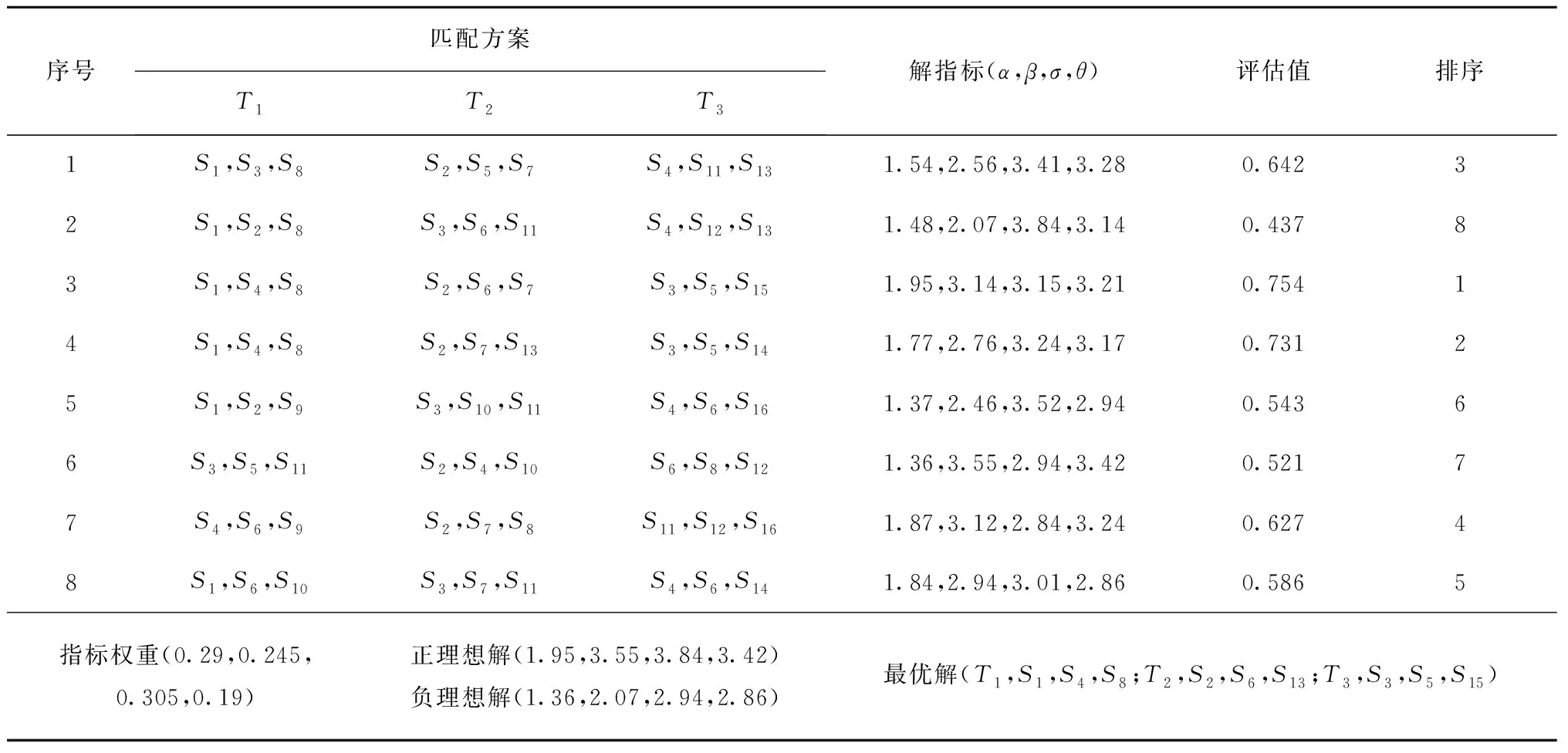
∀(0≤i (j≠k,i为j,k共同关注的服务); 式中设xij为决策变量,若第i个服务与第j个任务匹配则xij=1,否则xij=0。式(15)和式(16)为任务匹配优化的多个目标;式(17)表示复杂任务需匹配f个服务组,每个服务组中的服务单元数大于等于2;式(18)分别为匹配方案中服务对任务、任务对服务、任务间以及服务协同满意度的约束阈值;式(19)表示任务方存在竞争关系且共同关注服务数为1时,两任务均不匹配该服务,当共同关注服务数大于1时实现均等匹配。 制造任务匹配是一个包括4个子目标的多目标优化问题,以往研究通过给每个目标分配权重,将多目标优化转化为单目标优化问题,然后运用相应的线性规划和启发式算法求解[27]。当前多目标优化算法给每个子目标分配权重,但主观性较强,造成分配方案不合理,同时多个目标可能存在冲突,不能对多目标进行同步优化,而且只能得到一个最优解,难以满足用户的多样化需求。本文提出基于改进的非支配PSO算法获得Pareto最优解和Pareto前沿,运用加权TOPSIS方法评估得到实际情境中的最佳匹配结果。 PSO[28]算法中每个粒子为一个匹配方案,假定PSO搜索的空间是D维,群规模为M,Xi=(xi1,xi2,…,xiD)为第i个粒子目前的位置,Vi=(vi1,vi2,…,viD)为飞行速度,Pi=(pi1,pi2,…,piD)为当前最优位置,则粒子群当前的最优位置为G=(g1,g2,…,gD),i=1,2,…,M。对进行匹配的粒子不断迭代,其速度和最优位置变换如下: vid(t+1)=wvid(t)+c1r1(pid(t)- xid(t))+c2r2(gd(t)-xid(t)); (20) xid(t+1)=xid(t)+vid(t+1)。 (21) 式中:t为迭代代数;w为惯性因子;c1,c2为常数学习因子;r1,r2为随机数在(0,1)上的分布;d=1,2,…,D。通过不断更新粒子飞行速度和位置,当解收敛或满足最大迭代数时,获得任务匹配的全局最优解。在任务匹配过程中,粒子位置为整数,其更新公式变为: (22) 式中θ为随机变量且θ~U(0,1)。当vid(t+1)>0时,粒子向正方向变更一个单位;当vid(t+1)<0时,粒子向负方向移动一个单位;当vid(t+1)=0时,粒子遵循sig(θ)作随机移动,分别以1/3的概率向正、负方向移动一个单位或保持静止。同时,速度变更中的惯性因子 w=wmax-t(wmax-wmin)/Tmax。 (23) 式中:wmax,wmin为最大、最小惯性因子;t表示迭代数;Tmax表示最大迭代数。 wi(t)=(1+e-k)-1。 (24) 式中:wi(t)为第i个粒子在第t次迭代时的自适应惯性权重,其值在[0,1]分布。当k=0时,惯性权重wi(t)=0.5;当k变大时,wi(t)也随之变大,从而更好地促进搜索效率的提升。 通过最优种群更新机制加速PSO的收敛速度:对于1→t迭代,保存Xbest(t);对于从2→t到T迭代,如果Xbest(t-1)≤fb(t),则保存Xbest(t-1)=Xbest(t);如果Xbest(t-1)>fb(t),则保存Xbest(t)=fb(t)。最优种群更新方法能够避免种群早熟现象,提升搜索效率。 运用改进算法从位置变更后的粒子中以较小概率选择1维按式(21)和式(22)赋值,利用Pareto支配关系实现外部集合变更,引入新粒子时删除最拥挤解。根据所处位置选择最优粒子,无支配关系时随机选择粒子进行个体更新,并从拥挤距离靠前的粒子中选择粒子群进行全局优化更新,使解均匀地分布在Pareto前沿上。当收敛或达到最大迭代次数后,外部集为Pareto最优集,构造目标D维空间的Parto前沿。改进PSO算法流程如图5所示。 通过3.1节的算法得到多个任务匹配的Parto最优解,每个解包括服务满意度、任务满意度、任务间满意度和服务协同满意度4个指标。根据客户实际需求,运用加权TOPSIS方法可以从众多非支配解中选择一个最满意的结果,详细过程如下: (1)得到m个Pareto最优匹配方案,包括α,β,σ,θ,并构建评判矩阵R, R=(rij)n×m,i=1,2,…,n,j=1,2,3,4。(25) (2)利用熵权法和主观法分别得到客观、主观权重wo,ws,综合权重为 Wc=ϖ1wo+(1-ϖ1)ws。 (26) (3)将指标权重Wc引入评估矩阵中,R中每一行与权重相乘构建加权评估矩阵 (4)确定匹配方案的正理想解V+和负理想解V-: (28) (5)计算每个匹配方案到正、负理想解的距离,运用欧氏距离进行计算: (6)计算匹配方案与理想解的贴近度,得到方案的评估排序 (30) Ci贴近度越大,表明方案i离最优水平越近,应该选择贴近度最大的解作为最优方案。 针对智能汽车制造项目的实际需求,通过仿真实验平台,构造一个包括16个服务单元的服务协同网络,该网络拥有多种制造资源和能力,如图6所示。联盟接受3个存在竞争关系的制造任务T1,T2,T3,每个任务需要由λ个服务单元完成,根据业务要求给出λ=3。平台中的服务单元能够参与到不同任务中,具有自己的市场定位。平台提供的任务方评估值包括付款速度(B1)、可靠性(B2)、信誉(B3),服务评估值包括成本(A1)、时间(A2)、信誉(A3),任务方给出对匹配服务的期望值,服务方给出对分配任务的期望值,如表1和表2所示。 进一步给出3个任务在CP1个细分市场的额度和在CP2个优质资源的投资额,通过式(3)~式(7)得到任务间的竞争关联强度,如表3所示,表中0表示两个任务不存在竞争。给出服务间交易合作、资源共享和社会相似关系的属性值,聚合得到如表4所示的协同关系表,表中数值表示协同效应的大小,其中1表示服务与其自身的协同效应,本文不作考虑。 表1 任务方评估值和对服务的期望 制造任务任务QoT任务的期望值B1/周B2B3A1/万元A2/周A3T11180.7011240.99T21370.951580.95T3790.9317120.98 表2 服务单元的服务质量和市场定位 表3 任务竞争关联强度 云平台中心根据任务方的请求和服务方的市场定位,考虑竞争与协同效应的影响来实现双方满意的匹配,以达到平台受益的最大化。通过熵权法对仿真数据进行计算,得到任务对服务的评价指标权重为(0.27,0.35,0.38),服务对任务的评价指标权重为(0.25,0.43,0.32),服务社会关系的权重为(0.42,0.32,0.26)。采用第2.1节~2.3节提出的方法计算得到服务方满意度α、任务方满意度β、任务间满意度σ和服务间协同满意度θ,构建多目标任务双边匹配数学模型,运用于改进的非支配PSO算法和加权TOPSIS决策方案进行求解,得出最优的满意稳定匹配方案,其中T1匹配S1,S4,S8、T2匹配S2,S6,S13、T3匹配S3,S5,S15。 表4 服务协同满意度 运用MATLAB软件对改进粒子群算法进行编程。设粒子维度D为任务数3;粒子群规模M=400;最大迭代数Tmax=100;惯性因子wmin=0.6,wmax=1.1;学习因子c1=c2=0.8;外部集规模为100。通过多次实验,迭代50次后改进算法3个目标的函数平均适应度趋于平稳,满足收敛条件。同时,迭代50次后的非支配解比例也趋于稳定,为20%左右(如图7),算法时间为0.78 s。共获取8组Pareto最优解(如表5),运用加权TOPSIS从8组解中评估得到最优方案。运用熵权法得到解指标客观权重wo=(0.26,0.21,0.34,0.19),运用层次分析法得到主观权重ws=(0.32,0.28,0.27,0.13),主、客观权重的比重均为0.5,则解指标权重Wc=(0.29,0.245,0.305,0.16)。由此得到加权评估矩阵,通过抽取每一列中的最大值获取正理想解V+=(1.95,3.55,3.84,3.42),抽取每一列中的最小值获取负理想解V-=(1.95,3.55,3.84,3.42),然后利用式(29)~式(30)计算出每个方案到理想解的贴近度并进行排序。 采用TPOSISI方法评估得到的匹配方案3的贴近度排序最高,(T1,S1,S4,S8;T2,S2,S6,S13;T3,S3,S5,S15)为最佳匹配结果。对比方案3和方案4,两者只有两个差别的服务匹配。虽然方案4在任务间满意度上略大于方案3,但方案3的α,β,θ分别为1.95,3.14,3.21,均大于方案4的1.77,2.76,3.17,而且方案3中的服务组(S1,S4,S8),(S2,S6,S13),(S3,S5,S15)不仅具有良好的任务满意度和服务满意度,其组内单元还具有高水平的合作经验、资源共享等协同效应。因此,方案3能够高效地完成智能汽车制造任务,为最佳匹配结果。同时,由于T1与T3、T2与T3存在竞争关系,通过评估服务能力发现T1与T3的共同关注服务为S7,T2与T3的共同关注服务为S1。在进行服务匹配时,需要综合考虑任务间的竞争效应,禁止将S7匹配给T1,T3中的一个,将S1匹配给T2,T3中的一个,避免任务方因竞争均获得重要任务而离开匹配市场,导致云平台的交易量和收益降低。所获得的Pareto解已满足竞争约束,本文方法给出了多个满意的候选方案,如果执行中某一服务出现故障,已选定的方案难以执行,或者决策者偏好发生变化,则可从其他候选方案中挑选较为接近的方案替换,从而提升制造过程的柔性和环境适应性。 表5 Pareto最优解及匹配方案排序 为了说明本文模型的优势,实验2将本文模型与传统双向匹配(模型2)、考虑竞争效应的双向匹配(模型3)、考虑服务协同效应的双向匹配(模型4)3类模型进行对比分析,相关参数设置参照实验1,结果如表6所示。本文模型(模型1)下获得最优匹配方案1,模型2下获得最优匹配方案2,模型3下获得最优匹配方案3,模型4下获得最优匹配方案4。4类模型有相应的适应范围,能在其擅长的领域获取最优的结果,应根据实际应用背景选择最优的匹配策略。在本文模型下,方案1拥有最优的整体绩效0.754,其在任务满意度、服务满意度、任务间满意度和服务间协同要求4方面均有良好的表现;方案3拥有最优的任务间满意度,其整体绩效为0.724;方案2将T2与T3共同关注的服务S1匹配给T2,方案4将T1与T3共同关注的服务S7匹配给T1,违反了任务竞争关系约束,导致匹配方案无效。在模型2下,方案2拥有最优的任务满意度和服务满意度,其整体绩效最优,为0.658,而方案1、方案3和方案4相对较差。在模型3下,方案3拥有最优的任务间满意度3.52,整体绩效最优0.742;方案1虽然也考虑了竞争关系,但所占比重较小,整体绩效略差,为0.712;方案2和方案4因忽视竞争关系而导致匹配失败。在模型4下,方案4拥有最优的服务间满意度3.43和整体绩效0.724;方案1~方案3由于忽略了服务协同或者对服务协同的重视程度较低,导致整体绩效相对偏低。针对智慧云制造平台上任务和服务的特点,本文模型将任务间竞争效应和服务协同效应考虑到双边匹配过程中,具有明显的优势,更符合复杂实际制造的应用。其他模型和方法也有其适用的优势场景,应根据不同应用需求选择合理的匹配策略和方法。 表6 不同匹配方法结果的对比 智慧云平台为任务请求者和服务提供方提供了沟通交互、谈判协商和交易合作的场所,通过双向匹配机制实现了供需双方的合理匹配。由于平台上的任务方互相争夺市场份额和优质资源,存在竞争关系,竞争对手的匹配结果会影响自身的决策行为和感知满意度;同时,服务间存在多种社会关系和协作联盟,联盟中其他成员的选择也影响服务单元的任务偏好和满意度。因此,本文通过刻画任务竞争关联网络和服务协同网络,提出基于竞争与协同的一对多双边匹配方法,构建了任务双向匹配的多目标优化模型,并运用改进算法得到最佳匹配结果。改进算法具有良好的搜索效率和效果,适用于大规模任务匹配问题。而且通过实验证明了本文模型在竞争与协同环境下的优势,即能够获得贴近真实制造情景的最优解。分析了不同匹配模型和方法的适用情形,对比了不同应用背景下最优方案的差异。 文中只运用期望效用计算任务、服务双方满意度,忽视了决策主体对于收益和损失的不同态度,下一步将构建基于累计前景理论的双方满意度聚合方法;另外,服务间还存在不兼容、矛盾冲突等负协同效应,因此考虑服务间的正、负协同效应共同作用下任务双边匹配的决策问题也将是未来研究的内容。 参考文献: [1] PORTER M E, HEPPELMANN J E. How smart, connected products are transforming competition[J]. Harvard Business Review,2016,94(1/2):24. [2] BONVILLIAN W B. Advanced manufacturing policies and paradigms for innovation[J]. Science,2013,342(6163):1173-1175. [3] YAO Xifan, JIN Hong, ZHANG Jie. Towards a wisdom manufacturing vision[J]. International Journal of Computer Integrated Manufacturing,2014,28(12):1291-1312. [4] ZHANG Yingfeng, XI Dong, LI Rui, et al. Task-driven manufacturing cloud service proactive discovery and optimal configuration method[J]. The International Journal of Advanced Manufacturing Technology,2016,84(1):29-45. [5] BAO Beifang, YANG Yu, CHEN Qian, et al. Task allocation optimization in collaborative customized product development based on double-population adaptive genetic algorithm[J]. Journal of Intelligent Systems,2014,23(1):1-14. [6] LARTIGAU J, XU X. Cloud manufacturing service composition based on QoS with geo-perspective transportation using an improved artificial bee colony optimisation algorithm[J]. International Journal of Production Research,2015,53(14):4380-4404. [7] KOVARICKOVA B. Position of the manufacturing company in market environment[J]. Evaluation Engineering,2012,42(4):54-55. [8] IBRAHIM K, HADI G, TAHSIN C. An analytic hierarchy process and two-sided matching based decision support system for military personnel assignment[J]. Information Sciences,2008,178(14):2915-2927. [9] FAN Zhiping, YUE Qi. Strict two-sided matching method based on complete preference ordinal information[J]. Journal of Management Sciences in China,2014,17(1):21-34(in Chinese).[樊治平,乐 琦.基于完全偏好序信息的严格双边匹配方法[J].管理科学学报,2014,17(1):21-34.] [10] GALE D, SHAPLEY L. College admissions and the stability of marriage[J]. American Mathematical Monthly,1962,69(1):9-15. [11] ROUSSANOV N L, SAVOR P G. Marriage and managers’ attitudes to risk[J]. Management Science,2014,60(10):2496-2508. [12] KRISTALNY M, MIRKIN L. On the two-sided model matching problem with preview[J]. IEEE Transactions on Automatic Control,2012,57(1):204-209. [13] HAAS C, KIMBROUGH S O, CATON S, et al. Preference-based resource allocation: using heuristics to solve two-sided matching problems with indifferences[C]// Proceedings of the 10thInternational Conference on Grid Economics and Business Models. Berlin, Germany: Spinger-Verlag, 2013:149-160. [14] XU Hong, LIBaochun. Anchor: a versatile and efficient framework for resource management in the cloud[J]. IEEE Transactions on Parallel & Distributed Systems, 2013, 24(6):1066-1076. [15] KUANG Guijuan, ZENG Guosun, CAO Jie, et al. Satisfactory marriage method between cloud tasks and resources based on graph theory[J]. Acta Electronica Sinica,2014,42(8):1582-1586(in Chinese).[匡桂娟,曾国荪,曹 洁,等.基于图匹配理论的云任务与云资源满意“婚配”方法[J].电子学报,2014,42(8):1582-1586.] [16] CHENG Ying, TAO Fei, ZHAO Dongming, et al. Modeling of manufacturing service supply-demand matching hypernetwork in service-oriented manufacturing systems[J]. Robotics and Computer-Integrated Manufacturing,2017,45:59-72. [17] ZHAO Jinhui, WANG Xuehui. Two-sided matching model of cloud service based on QoS in cloud manufacturing environment[J]. Computer Integrated Manufacturing Systems,2016,22(1):104-112(in Chinese).[赵金辉,王学慧.基于服务质量的云制造服务双向匹配模型[J].计算机集成制造系统,2016,22(1):104-112.] [18] YANG Jianmei, LU Lyuping, XIE Wangdan, et al. On competitive relationship networks:a new method for industrial competition analysis[J]. Physica A Statistical Mechanics & Its Applications,2007,382(2):704-714. [19] SUN Yong , TAN Wenan, LI Lingxia, et al. A new method to identify collaborative partners in social service provider networks[J]. Information Systems Frontiers,2016,18(3):565-578. [20] BANDO K, KAWASAKI R, MUTO S. Two-sided matching with externalities:a survey[J]. Journal of the Operations Research Society of Japan,2016,59(1):35-71. [21] BODINEBARON E, LEE C, CHONG A, et al. Peer effects and stability in housing assignment[C]//Proceedings of International Symposium on Algorithmic Game Theory. Berlin, Germany: Springer-Verlag, 2011: 117-129. [22] MUMCU A, SAGLAM I. Stable one-to-one matchings with externalities[J]. Mathematical Social Sciences,2010,60(2):154-159. [23] NGUYEN T, PEIVANDI A, VOHRA R. Assignment Problems with Complementarities[J]. Journal of Economic Theory,2016,165(12):209-241. [24] BANDO K. Many-to-one matching markets with externalities among firms[J]. Journal of Mathematical Economics,2012,48(1):14-20. [25] BANDO K. A modified deferred acceptance algorithm for many-to-one matching markets with externalities among firms[J]. Journal of Mathematical Economics,2014,52(3):173-181. [26] LEHRER E, TEPER R. Subjective independence and concave expected utility[J]. Journal of Economic Theory,2015,158(7):33-53. [27] NAYAK A. Multi-objective process planning and scheduling using controlled elitist non-dominated sorting genetic algorithm[J]. International Journal of Production Research,2015,53(6):1712-1735. [28] LIU Li , LI Yunfei , ZHANG Miao, et al. QoS oriented PSO algorithm for cloud service composition modeling[J]. Applied Mechanics & Materials,2014,577:931-934.3 基于改进的非支配粒子群和加权TOPSIS决策匹配优化方法
3.1 改进粒子群优化算法
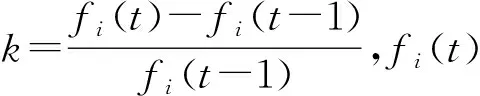
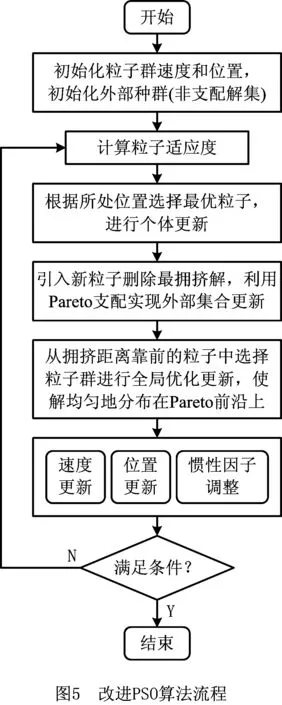
3.2 基于加权TOPSIS最优决策方法
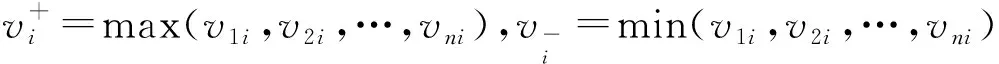
4 实验分析
4.1 实验设计


4.2 结果分析

5 结束语
