基于磁性材料的中心力场演示实验仪

武家铭

(执信中学，广东 广州 510080)

中心力场作用下物体的运动规律问题是物理学中的基本问题. 天体物理中行星在引力作用下绕恒星的公转[1]和类氢原子中核外电子在电磁力作用下绕原子实运动的玻尔模型属于单中心力场问题[2]，月球在太阳和地球共同作用下的运动以及双原子分子中电子的运动则属于双中心力场问题，而晶体内电子和空穴等带电载流子在晶格产生的周期性电场中的运动则属于多中心力场问题[3]. 可以说，中心力场问题贯穿了物理学的许多分支领域，是一个具有重要意义的基本问题，因此常被设置为物理教学的重要内容[4-5].

从原子到天体，中心力场问题涉及的物体形态各异，几何尺度跨度达数十个数量级，不易理解，若能在课堂上模拟和演示不同尺度、不同数量中心力场下物体的运动，将有助于学生理解该问题. 为此，设计并制作了中心力场演示实验装置. 该装置利用纽扣型磁铁产生的磁场模拟不同形式的中心力场，利用可被磁化的金属小球作为在力场中运动的物体，使用高速摄像机拍摄小球运动的视频，结合分析软件[6]，提取金属小球在力场中运动的轨迹、速度、加速度、动量等多种动力学参量. 在此基础上，编写程序对小球的运动进行数值模拟，并将模拟结果与实验结果进行对比.

1 实验装置

装置的原理如图1所示，分成3层，全部由有机玻璃制作，上层和下层厚度为5mm，中间层厚度为8mm. 中间层按周期性结构制作了二维的小孔阵列，小孔间距为20mm. 小孔直径为10mm，可放置直径为10mm的纽扣形铷铁硼强磁铁. 上下层夹紧后，孔内的磁铁位置固定，不会因外作用而翻转. 让被磁化的小金属球在上层有机玻璃板上移动，以模拟中心力场中的运动物体. 由于二维小孔阵列内放置磁铁的位置、数量和磁铁的极性可自由选择，故可用来模拟单中心、双中心、多中心甚至周期性中心等多种力场中物体的运动. 金属小球通过导轨滑入力场，导轨的倾斜角度和长度可调，故小球的数量、大小和初始运动速度等参量也可在一定范围内定量调节.

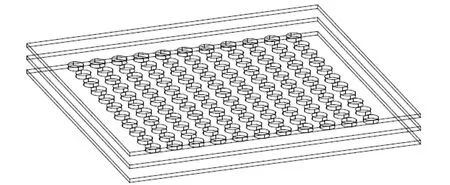
图1 中心力场演示实验装置原理图

图2是演示装置实物的局部图，模拟具有4个中心的力场. 将纽扣形磁铁堆叠成柱状可阻止金属球运动到磁铁的顶部，避免后续的受力分析必须同时考虑磁铁边界之内和之外2种情况，将数值模拟简化为二维模型.

图2 中心力场实验装置实物图

小球进入力场后，采用最快的拍摄速度为500帧/s的JVCGC-P100型高速摄像机拍摄小球的运动视频，导入Tracker视频分析软件进行分析，提取小球的位置和速度随时间变化的定量数据. 计入小球的质量后，还可进一步计算小球的动量和动能.

2 实验结果和数值模拟

2.1 实验结果

小球沿斜面滑入中心力场后，呈现出复杂多样的运动轨迹，且对实验条件很敏感. 小球的运动轨迹与其大小、入射速度、入射方向，磁铁的位置、数量，以及小球与磁铁之间的距离等多种因素有关. 但在磁铁位置和数量确定、小球大小确定、斜面的倾斜角度确定、小球释放位置确定的情况下，小球运动的轨迹基本可以重现. 图3所示为Tracker软件提取的单个中心时小球的运动轨迹，展示了小球运动完全不受中心力场影响，在中心力场作用下运动方向发生偏转，被力心束缚等多种不同的受力情况. 图3中十字线的交点为力场中心的位置. 图4则为双中心力场下小球的1种运动轨迹.

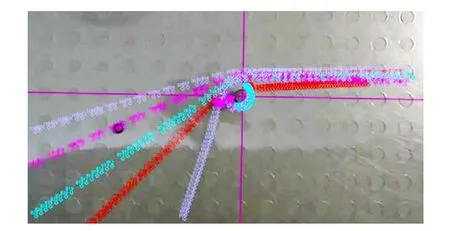
图3 单中心力场下运动轨迹的提取

图4 双中心力场下运动轨迹的提取

2.2 运动轨迹的数值模拟

可磁化小球在纽扣形磁铁产生的中心力场中的受力与磁场的梯度成比例，表现为非线性力[7]，且不满足距离的平方反比关系，故运动轨迹的精确解难以得到. 本文采用半经验的方法进行数值模拟. 先将小球用细绳黏紧，用数字式拉力计牵引细绳，测出拉力F随小球与磁铁中心距离x的变化数据，采用式(1)所示的多项式进行拟合，得到确定的(a0，…，a6)参量后，再代入运动方程，用数值积分的方法计算出小球的运动轨迹，即

(1)

实验中，小球的质量为3.47 g，计算的时间间隔dt与高速摄像机的500帧/s的拍摄速度匹配，取dt=2 ms.

用Matlab编制[8]的双中心力场下图形化仿真计算程序界面如图5所示，可手动输入2个力心的位置(Cx,Cy)、小球受力拟合公式的系数、小球初始位置(x0,y0)、初始速度(vx0,vy0)、计算时间间隔dt、计算总时间T等参量. 图中的长度统一用m为单位. 实验中，2个力心的位置分别为(50 mm，0)，(-50 mm，0),小球初始位置为(-200 mm,-40 mm)，初始速度为139 mm·s-1,44.79 mm·s-1，拟合函数为

0.195 3x3+0.016 1x4-0.000 7x5+0.000 1x6.

(2)

图5 双中心力场图形化仿真计算程序计算结果

输入图4实验结果对应的初始参量后，计算得到的小球轨迹如图5中的曲线所示，与实验结果基本一致. 图6所示为小球被四中心力场束缚时的闭合轨迹，也与实验结果对应.

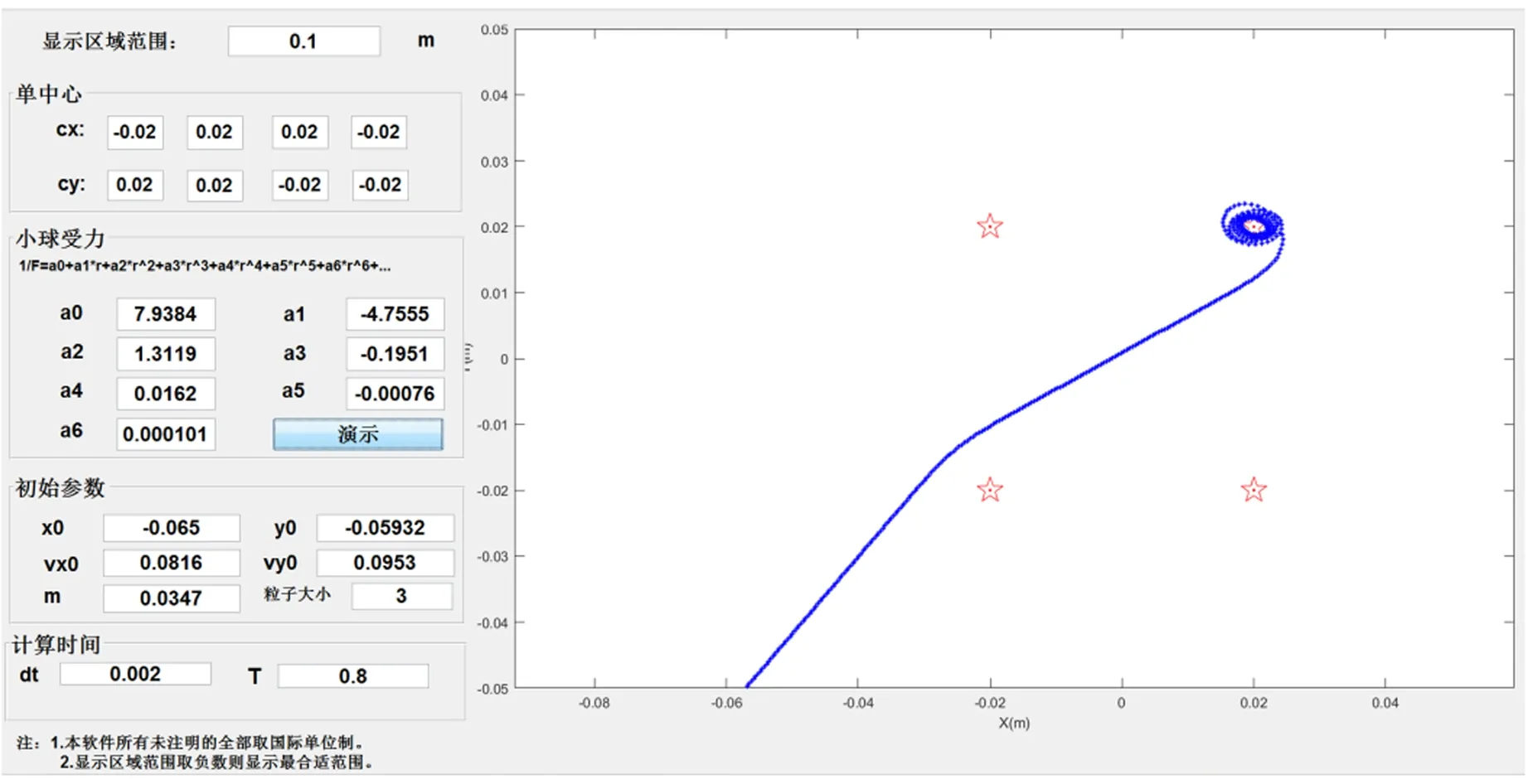
图6 被四中心场束缚时的运动路径

3 结束语

实验和数值模拟结果表明：基于二维圆孔阵列的多中心力场运动演示装置可以综合演示单中心、双中心、四中心甚至周期性中心力场内物体的运动情况，且能够方便调控力心的数量、位置及运动物体的大小、 初始位置和速度等参量. 采用半经验的方法拟合小球受力公式后，数值计算得到的运动轨迹与实验结果基本符合. 实验和模拟结合，可以较好地演示物理教学中涉及中心力场的运动问题.

参考文献：

[1] 薛中伟. 行星运动的力学分析[J]. 山西财经大学学报,2011,33(2):265-266.

[2] 郑乐民. 原子物理[M]. 北京: 北京大学出版社,2010.

[3] 蒋平，徐至中. 固体物理简明教程[M]. 上海：复旦大学出版社,2007.

[4] 张铁强. 大学物理学(下册)[M]. 北京:高等教育出版社,2007.

[5] 人民教育出版社，课程教材研究所，物理课程教材研发中心. 普通高中课程标准实验教科书·物理(选修3-1)[M]. 北京：人民教育出版社,2010.

[6] Tracker4.85 05Apr 2014 Douglas Brown help文件[M]. 2014.

[7] 赵凯华，陈熙谋. 新概念物理教程·电磁学[M]. 北京:高等教育出版社,2006.

[8] 刘浩. MatLab R2014a 完全自学一本通[M]. 北京:电子工业出版社,2015.