基于单T网络的忆阻混沌电路

陈菊芳，徐 影，于倩倩

(东北师范大学 a.物理学院；b.物理学国家级实验教学示范中心(东北师范大学)，吉林 长春 130024)

2008年美国惠普实验室采用纳米技术成功实现具有“记忆”特性的元件——忆阻器[1]，电路设计的基础元件由电阻、电容和电感增加到了4个. 由于忆阻器是有记忆功能的非线性电阻，其潜在的应用价值引起了国内外学者的广泛关注，其中利用忆阻的非线性特征实现混沌电路是研究的热点之一. 忆阻器的磁通量φ与累积电荷q之间的关系用φ-q或q-φ平面上的曲线f(φ,q)=0来确定[1-3]. 当f(φ,q)=0由磁通的单值函数表示时，称为磁控忆阻器，特性曲线的斜率W(φ)=dq(φ)/dφ称为忆导. 忆阻器模型有多种，较为常见的是分段线性和三次光滑模型. 目前大多数忆阻电路是通过用不同忆阻器来替换蔡氏电路中的蔡氏二极管，得到一系列的蔡氏忆阻混沌电路[4-7]. 文献[8]利用文氏桥振荡器和忆阻器实现了忆阻混沌电路，文献[9]利用双T网络和忆阻器设计出了忆阻混沌电路，但忆阻器采用的均为分段线性模型.

本文采用RC单T选频网络构成的振荡电路和三次光滑型忆阻器设计了2种混沌电路. 忆阻器三次光滑的非线性函数为q(φ)=aφ+bφ3，由此可得到忆导为

W(φ)=a+3bφ2,

(1)

其中a>0,b>0.RC单T振荡电路和忆阻器的耦合方式不同，得到不同特性的忆阻混沌系统，并进行了电路仿真实验. 由于忆阻器的记忆特性，忆阻混沌电路比一般混沌电路具有更丰富的动力学行为. 虽然目前忆阻器还未商品化，在电路上只能用等效电路来模拟，但将来能以经济实惠的材料制作出既便宜又实用的第4种元器件，即可用忆阻器代替非线性电路，使混沌电路既简单又易实现.

1 并联型忆阻混沌电路

1.1 忆阻混沌电路

设计的并联型忆阻混沌电路如图1所示. 虚线框内的电路为单T正弦波振荡电路，R2，C2，R3，C3构成单T选频网络，起选频兼正反馈功能，与该网络常用的带阻滤波特性不同，设R2=R3=R0，C2=C3=C0，按照图1电路的连接方式，可求得运放A1同向端电压v+1与输出端电压vo1之比，即正反馈系数为

(2)

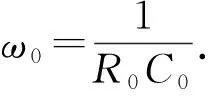
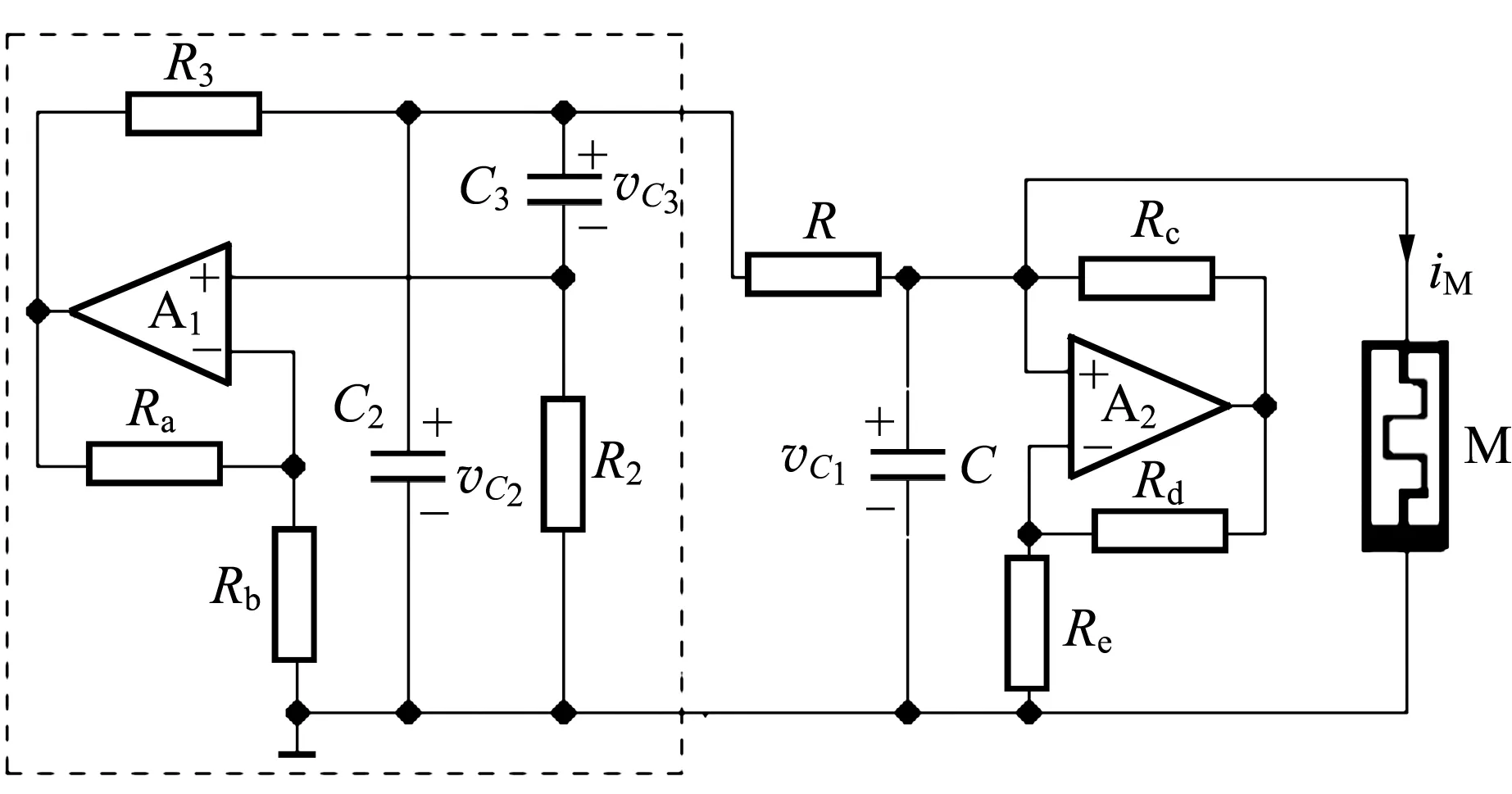
图1 并联型忆阻混沌电路

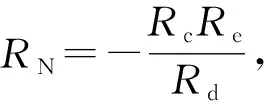
忆阻器的电流为

即可得到相应忆导值的表达式为

(3)

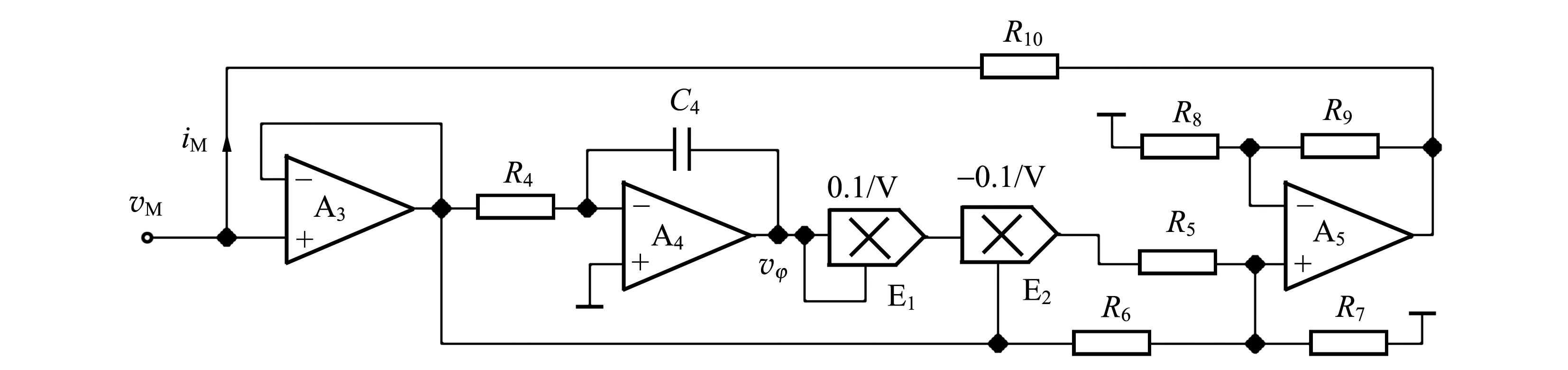
图2 磁控忆阻器模拟电路

忆阻器和振荡电路通过电阻R和电容C构成的低通滤波电路进行耦合，电容C与忆阻器并联，借助于忆阻器的非线性特性，若选择合适的电路参量，可产生混沌信号.

根据基尔霍夫定律，得到图1电路的状态方程为

(4)

选取R2=R3=R0=0.2 kΩ，C2=C3=C0=100 nF，Ra=22 kΩ，Rb=10 kΩ，Rc=Rd=1 kΩ，Re=0.98 kΩ，R4=0.2 kΩ，C4=100 nF，R5=1 kΩ，R6=10.6 kΩ，R7=R9=9 kΩ，R8=914 Ω，R10=1 kΩ，R=1.33 kΩ. 通过改变电容C，可观察到电路呈现丰富的动力学行为.

与一般混沌系统不同，令(4)式各方程等号左端为零，可得该式的平衡点为集合B={(vC1,vC2,vC3,-vφ)|vC1=vC2=vC3=0,-vφ=c}，c是常量，即-vφ坐标上的点集均是平衡点. 通过对(4)式在平衡点处的稳定性分析知，在C=3～50 nF范围，平衡点集B除零特征根之外的3个特征根的实部不都为负，说明在此范围内平衡点集B是不稳定的，这也可通过图3所示的分岔图和Lyapunov指数谱进一步证明. 为清晰可见，图3(b)只画出前3个Lyapunov指数，第4个Lyapunov指数只画出一部分，当有1个指数为正时表明系统是混沌的. 由图3(a)可见，随着电容C逐渐减小，图1电路的运行轨迹从无穷发散突变为不稳定的周期轨道，经过倍周期分岔后进入混沌轨道，混沌轨道经切分岔进入5周期窗口，再产生Hopf分岔演变成混沌轨道带，再进入新的混沌轨道，直至发散而趋近无穷，在混沌带中电路又存在若干个周期窗口.

由于篇幅所限，图4给出了几种典型的周期轨道、混沌轨道的数值计算结果，其中(a)，(b)和(c)为C取不同值时-vφ与vC1的相图，它们分别呈现2周期、单涡卷混沌和双涡卷混沌吸引子. (d)，(e)和(f)为对应的忆阻器的伏安特性曲线，印证了忆阻元件无论在周期态还是混沌态所呈现出的斜“8”型的伏安特性.

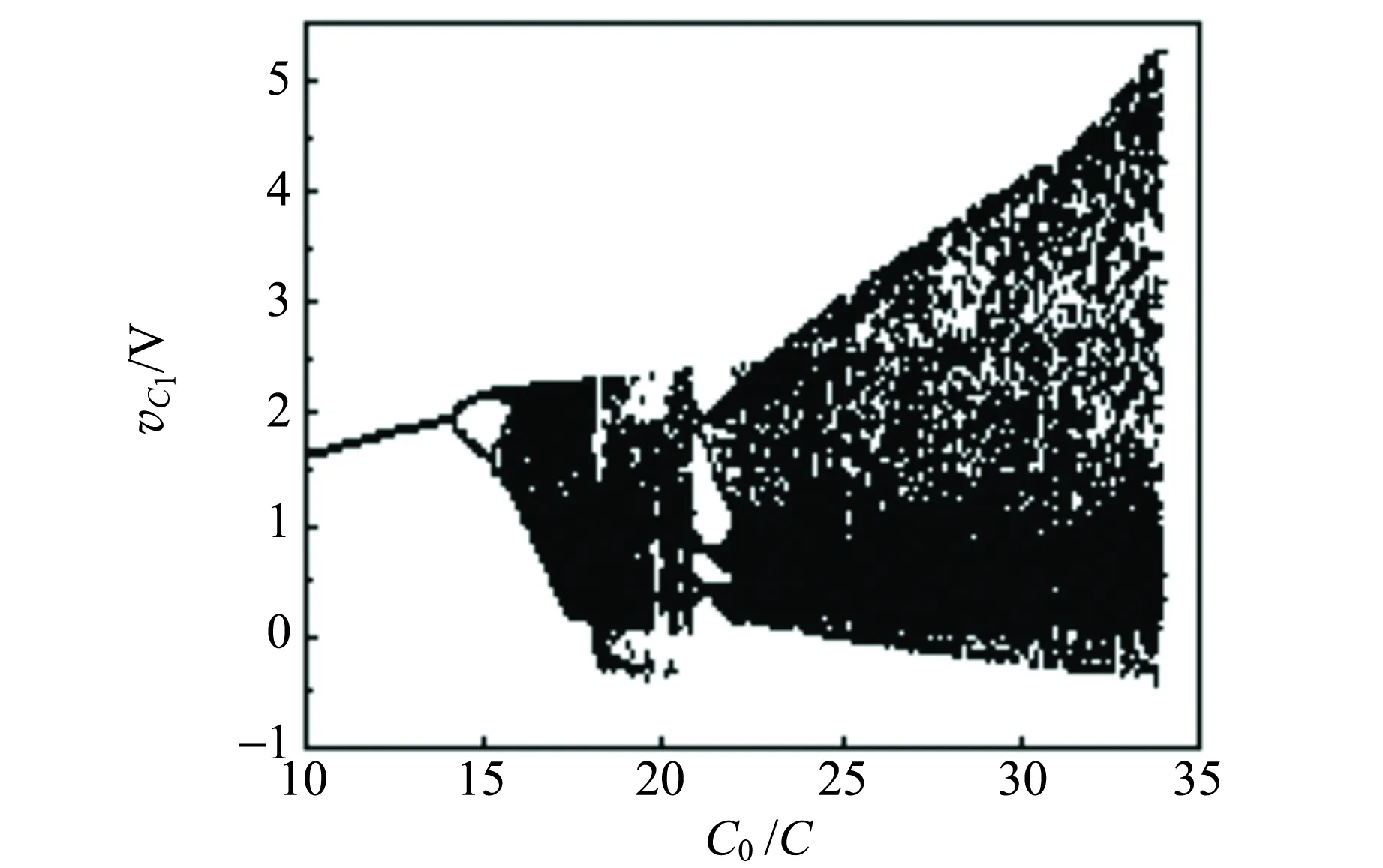
(a) vC1的分岔图

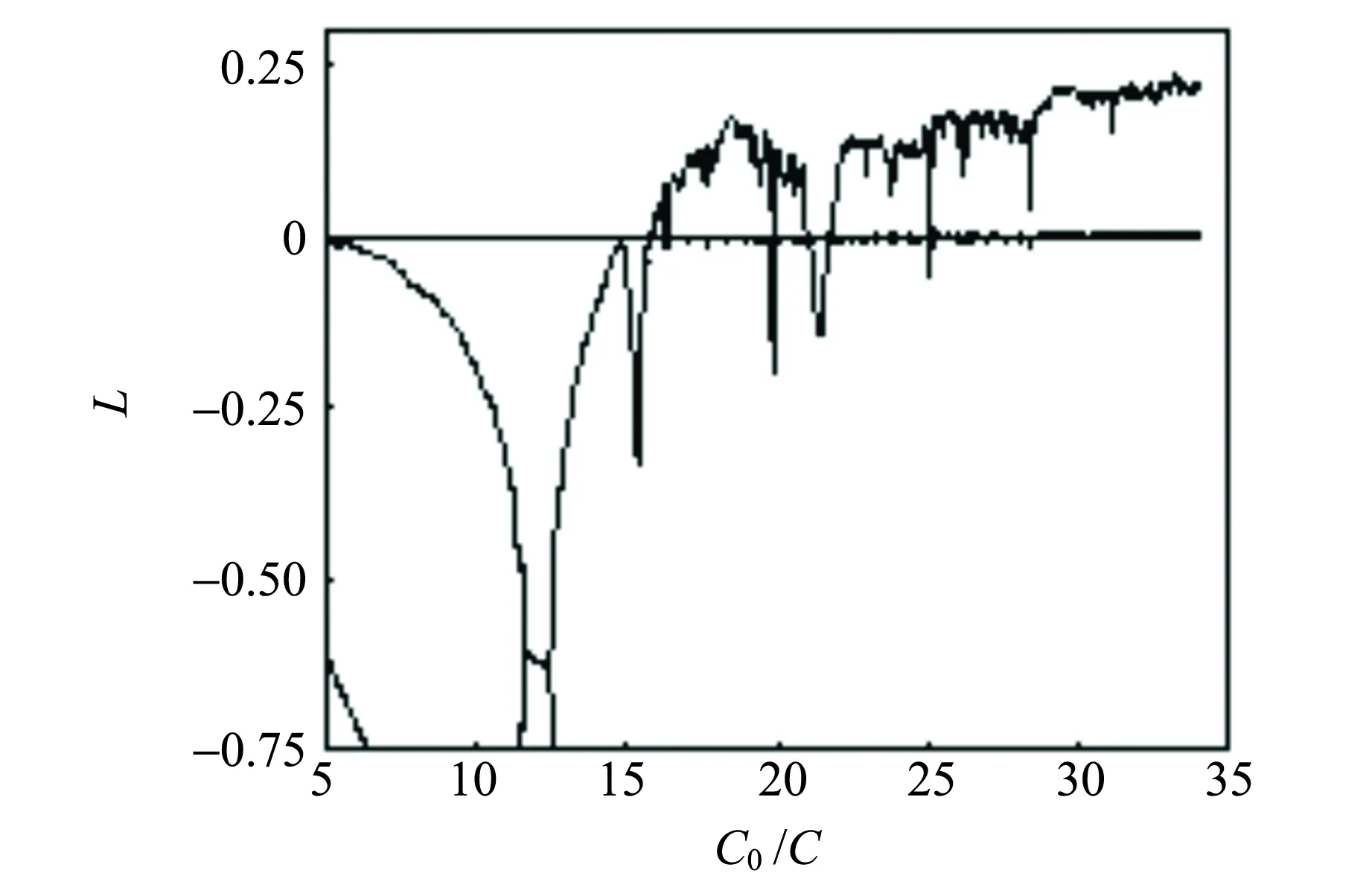
(b) Lyapunov指数谱

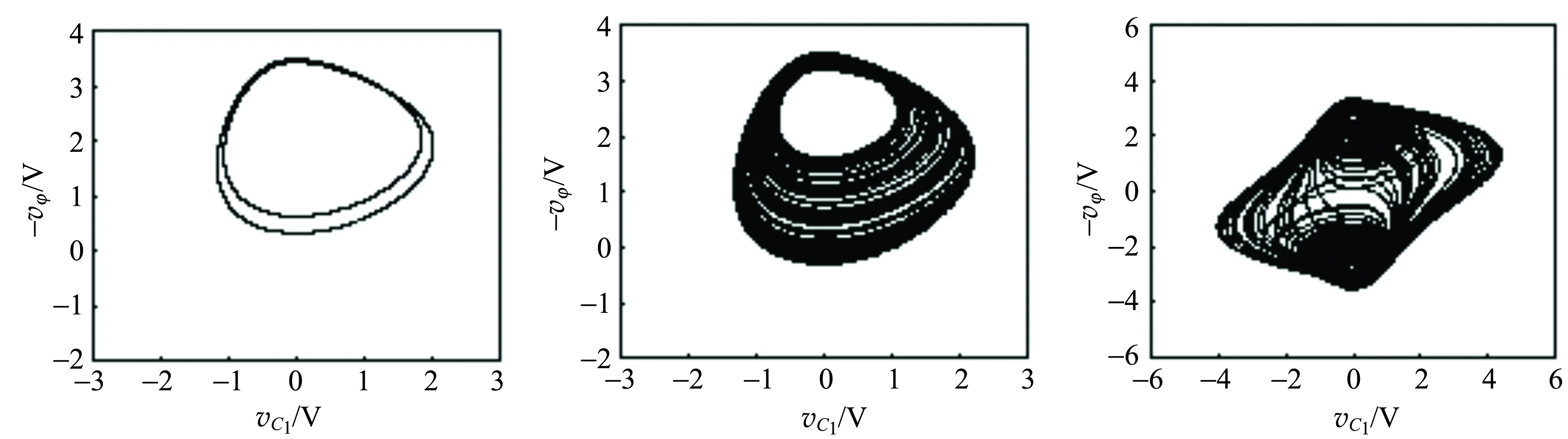
(a) C=7.0 nF (b) C=6.2 nF (c) C=3.3 nF

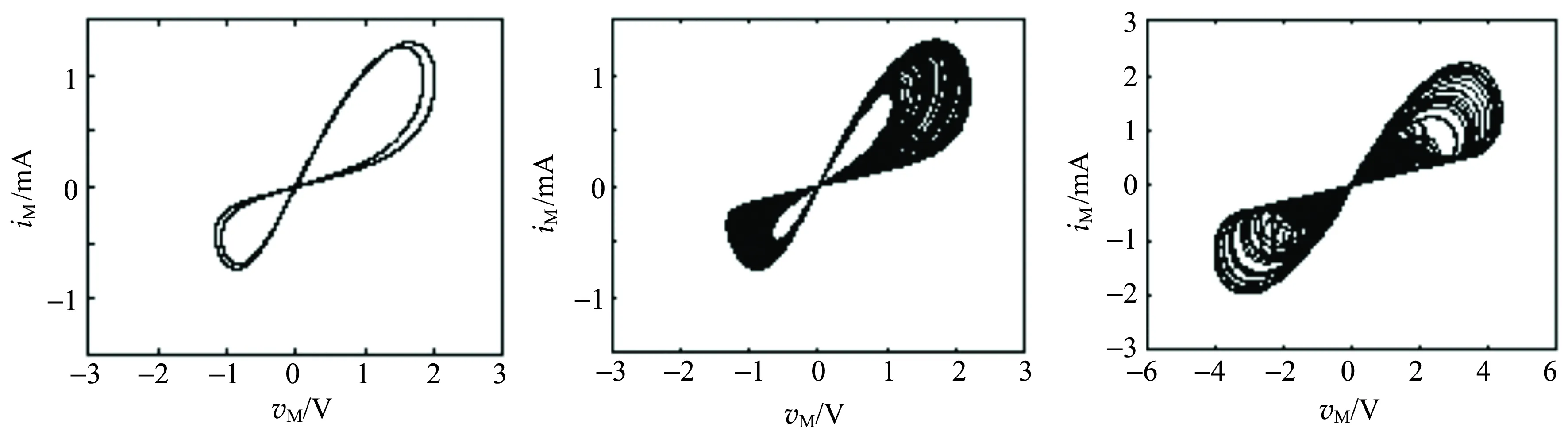
(d) C=7.0 nF (e) C=6.2 nF (f) C=3.3 nF图4 C取不同值时方程(4)数值计算的结果

1.2 电路仿真实验结果

为了验证设计电路的正确性，利用Multisim电路仿真软件进行了电路实验. 图5是当电容C取不同值时的部分实验结果，其中(a)，(b)和(c)为-vφ与vC1的相图，它们分别呈现2周期、单涡卷混沌和双涡卷混沌吸引子. (d)，(e)和(f)为对应的忆阻器的伏安特性曲线，忆阻电流iM通过取样电阻R10两端电压获得，即v10=iMR10，为了观测忆阻特性方便，选取R10=1 kΩ.

与图4结果比较可见，电路实验结果与数值计算结果得到的相图基本一致，只是电容C值稍有不同.

(a) C=6.25 nF (b) C=5.6 nF (c) C=3.3 nF

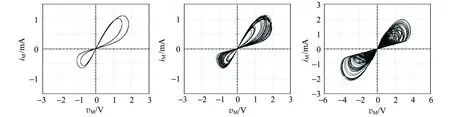
(d) C=6.25 nF (e) C=5.6 nF (f) C=3.3 nF图5 电路仿真的结果

2 串联型忆阻混沌电路

串联型忆阻混沌电路如图6所示. 耦合电容C与耦合电阻R并联，再与忆阻器串联，其他电路结构不变，此时忆阻器两端的电压变为vM=vC1+vC2. 虽然电路结构变化不大，但电路的动力学行为却不同.

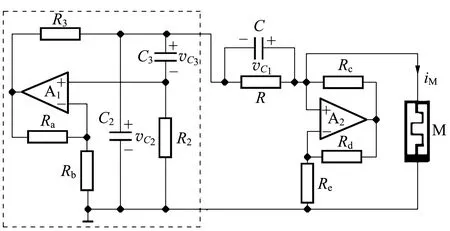
图6 串联型忆阻混沌电路

由图6得到电路的状态方程为选取Ra=20.5 kΩ，R5=1.5 kΩ，R6=10 kΩ，R8=1.3 kΩ，R=2 kΩ，其他电路元件参量与图1混沌电路相同. 电容C由大至小变化，画出变量vC1变化的分岔图如图7(a)所示. 可见，当电容C>10 nF时，电路处于周期状态，且变量vC2有着与其他变量不同的振荡频率，称为电路存在快慢效应现象. 选取C=12.5 nF，画出vC1与vC2的时域波形如图7(b)和(c)所示，vC2为1周期态，其频率为8.0 kHz，vC1为3周期态；当C=10 nF时，电路状态发生突变，且所有变量都变为1周期态，即电路快慢效应现象消失，随着C的减小，电路发生倍周期分岔后进入混沌状态；混沌轨道经切分岔进入3周期窗口，再产生Hopf分岔进入混沌轨道，再2次进入5周期窗口，直至当C减小至1 nF左右，电路状态发生突变，进入周期振荡状态，电路又出现快慢效应现象.

取C=2.5 nF，数值计算系统(5)的Lyapunov指数为：0.140 0，0.007 7,0.006 2，-4.116 7，在误差允许范围内存在正数，说明此时电路处于混沌状态. 分别画出-vφ与vC1的相图、忆阻器的伏安特性曲线如图8所示，表明它们是双涡卷混沌吸引子.

图9为C=2.5 nF时电路仿真结果，与数值计算结果基本一致，验证了设计电路的正确性.

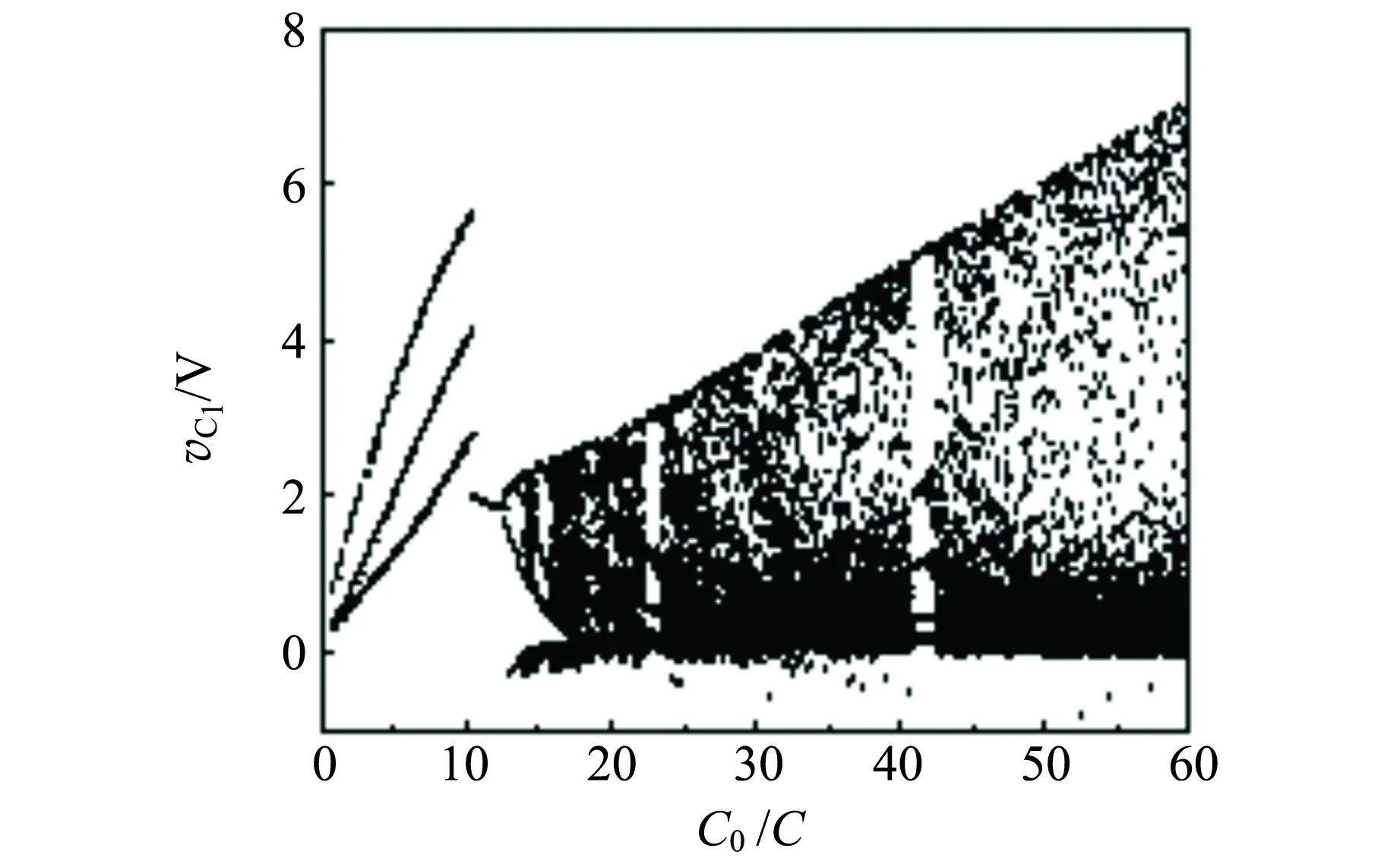
(a) vC1的分岔图

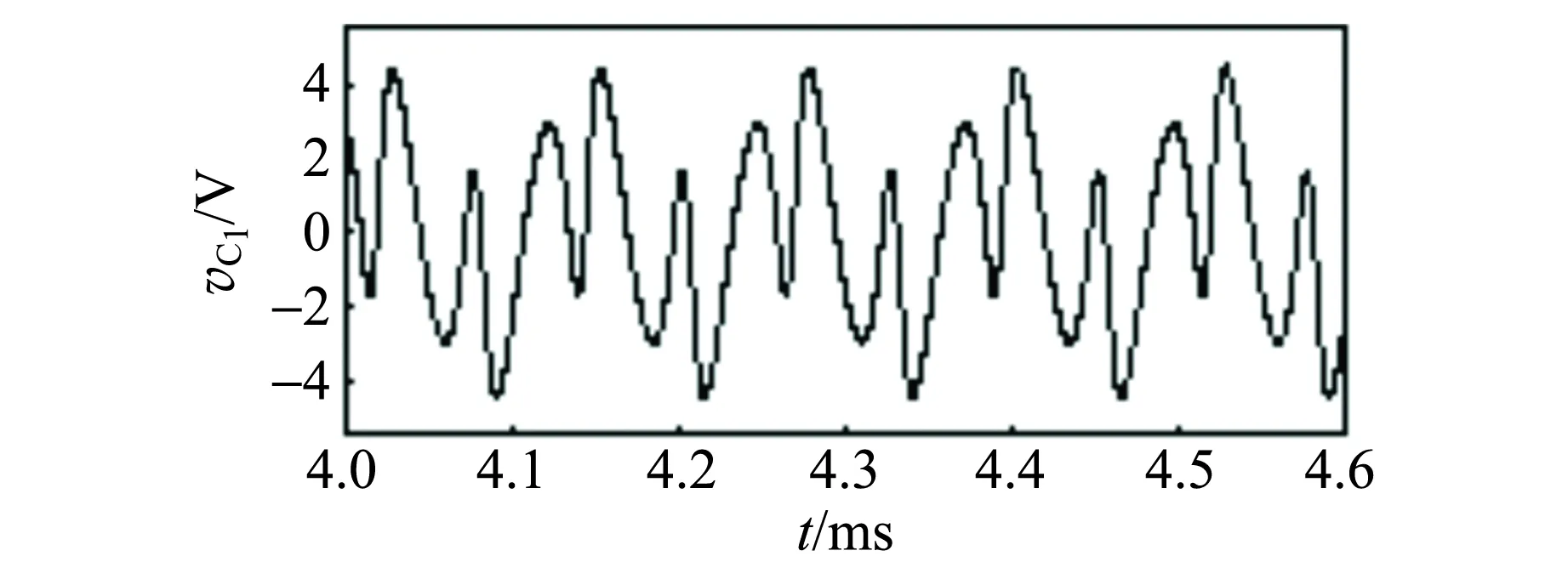
(b) vC1的时域波形图

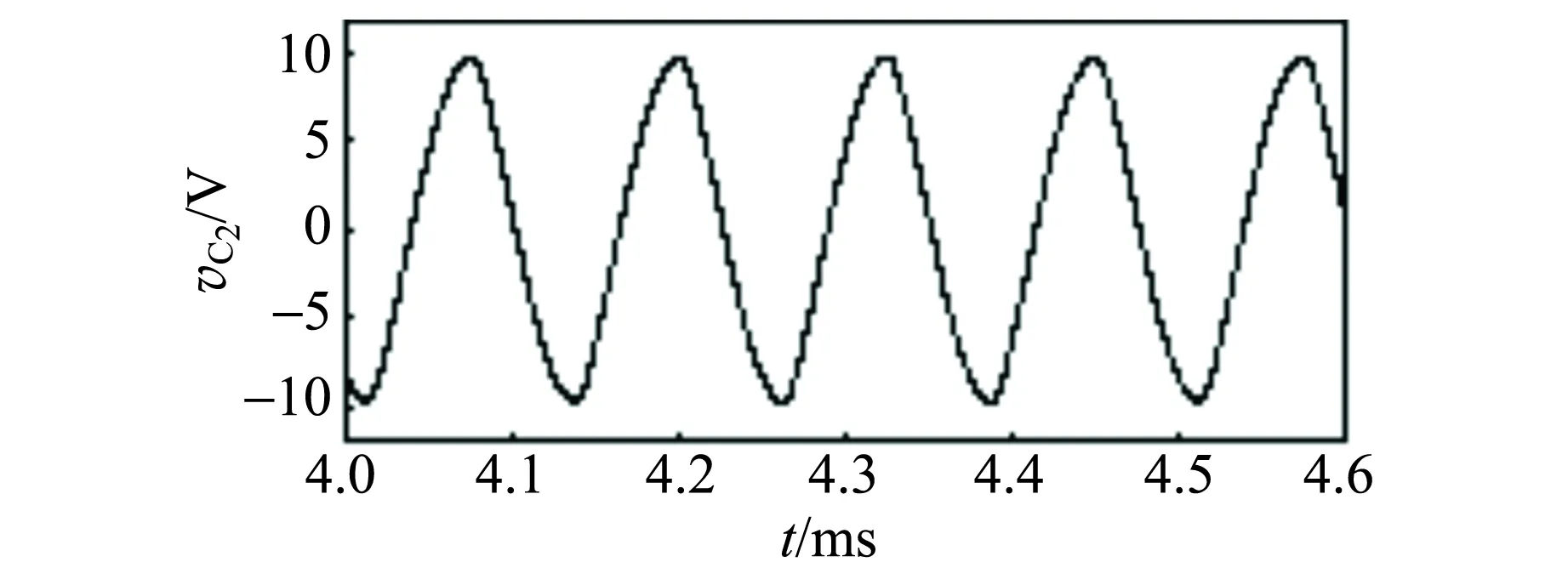
(c) vC2的时域波形图图7 电容C变化时方程(5)数值计算的结果

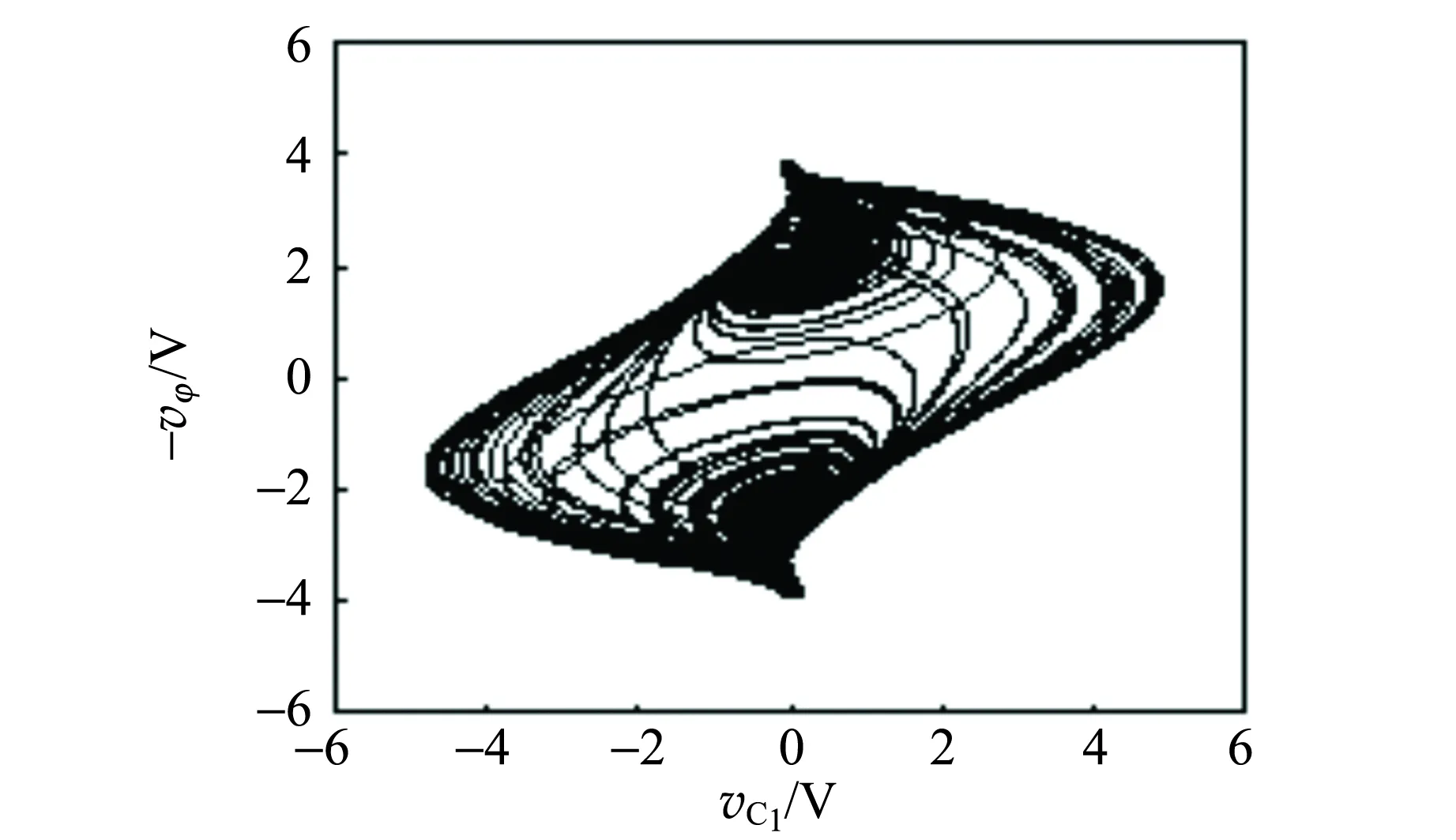
(a) 混沌吸引子

(b) 忆阻器的伏安特性曲线图8 C=2.5 nF数值计算的结果

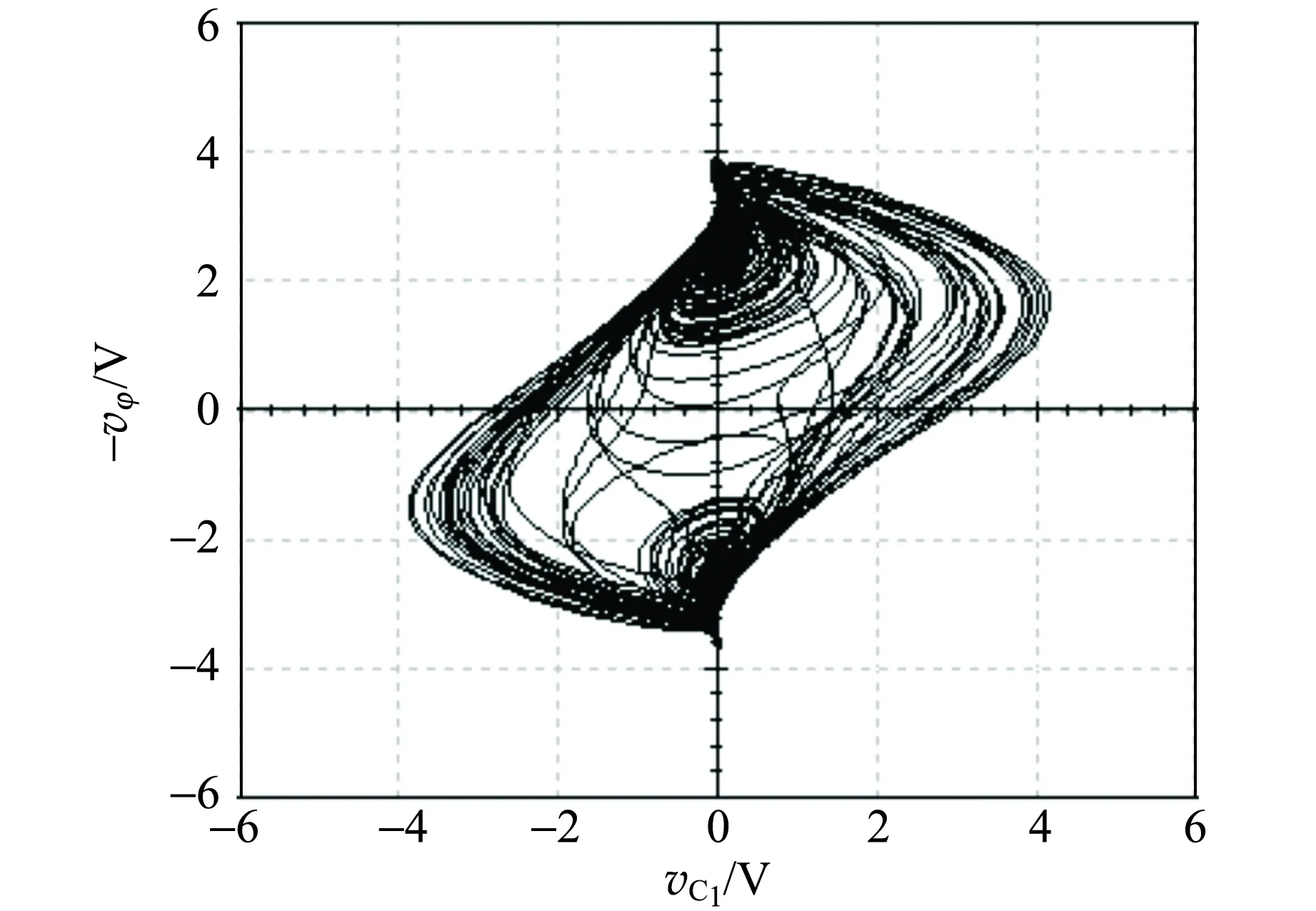
(a) 混沌吸引子

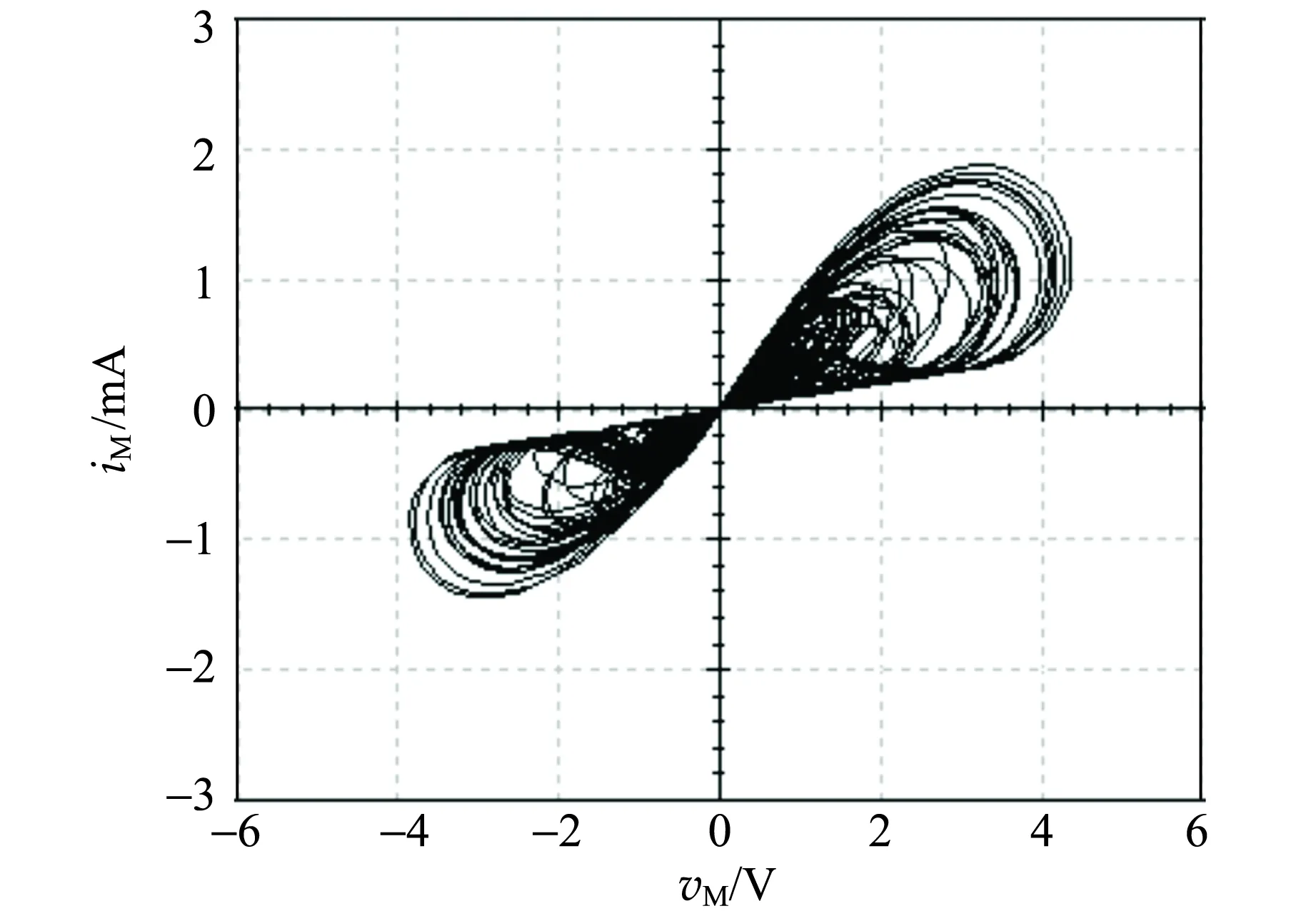
(b) 忆阻器的伏安特性曲线图9 C=2.5 nF电路仿真结果

3 结束语

利用RC单T选频网络构成的正弦波振荡电路与忆阻器通过不同的耦合方式设计出了2种忆阻混沌电路，并通过分岔图、Lyapunov指数和相图等方法分析了电路的基本动力学行为，观测到了当耦合电容C值变化时电路出现的诸如倍周期分岔、周期窗口、快慢效应等复杂的动力学行为. 对这2种忆阻混沌电路进行了电路仿真研究，得到的结果与数值计算的结果基本一致，进一步验证了忆阻混沌电路的正确性和有效性. 由于所设计的电路不含电感，因而具有很好的鲁棒性.

参考文献：

[1] Strukov D B, Snider G S, Stewart G R, et al. The missing memristor found [J]. Nature, 2008,453(1):80-83.

[2] Chua L O. Memristors-the missing circuit element [J]. IEEE Transactions on Circuit Theory, 1971,18(5):507-519.

[3] Chua L O, Kang S M. Memristive devices and systems [J]. Proceedings of the IEEE, 1976,64(2):209-223.

[4] Itoh M, Chua L O. Memristor oscillators [J]. International Journal of Bifurcation and Chaos, 2008,18(11):3183-3206.

[5] Bao B C, Xu J P, Zhou G H. Chaotic memristive circuit: equivalent circuit realization and dynamical analysis [J]. Chinese Physics B, 2011,20(12):120505.

[6] 杨芳艳,冷家丽,李清都. 基于Chua电路的四维超混沌忆阻电路[J]. 物理学报,2014,63(8):080502.

[7] 包伯成,刘中,许建平. 忆阻混沌振荡器的动力学分析[J]. 物理学报,2010,59(6):3785-3793.

[8] 李志军,曾以成. 基于文氏振荡器的忆阻混沌电路[J]. 电子与信息学报,2014,36(1):88-93.

[9] Li Zhi-jun, Zeng Yi-cheng. A memristor oscillator based on a twin-T network [J]. Chinese Physics B, 2013,22(4):040502.