集装箱码头送箱集卡预约与场桥调度协同优化
2018-06-29马梦知范厚明计明军郭振峰
马梦知,范厚明,计明军,郭振峰
(大连海事大学交通运输工程学院,辽宁大连116026)
0 引言
集装箱码头经营者和研究者一直在探索提升码头集港效率的新方法,以适应货主和船公司越来越高的集港要求.传统集港方式对于送箱时间普遍没有约束,存在较大的随机性,且码头与港外堆场缺少信息的交互沟通,高峰时段集中到港使得场桥等设备使用不平衡,甚至超负荷运转.因此,迫切需要优化调度场桥,合理分配集港时间,从而缓解高峰时段闸口或堆场拥堵及场桥“供不应求”的问题.
针对场桥在箱区间的调度问题,Zhang等[1]以堆场所有规划时段未完成作业量的总和最小为目标建立混合整数规划模型,求取场桥最佳的移动时间和路径,但忽略了送箱集卡不会在时段开始之初就全部到达箱区这一客观事实.因此,Linn等[2]在对箱区和场桥类型进行判断的基础上,建立了以各时段堆场未完成作业量最少为目标的场桥调度模型,但不能保证所有时段堆场未完成的作业量总和最小.李建忠[3]构建以所有时段堆场未完成的作业总和及场桥闲置时间最小为目标的规划模型,并采用基于启发式方法的Lagrangian松弛算法求解模型.
目前,国内外已有港口利用集卡预约系统对集卡到港时间进行管理,考虑到未按预约时段集港的惩罚成本(集卡早到时需在缓冲区内等待,而晚到则需要船放箱才能装船[4]),集卡都会尽量准时到港,因此,根据预约份额制定的场桥调度计划更准确.针对集卡到港时间管理的问题,Zhang等[5]构建了闸口和堆场二级排队网络,以最小化集卡平均周转时间为目标建立集卡预约优化模型,但没有考虑到预约机制给集卡司机造成的不便.因此,Chen G.等[6]以同时最小化集卡等待时间和预约前后集港时段调整的集卡数为目标建立集卡预约优化模型.曾庆成等[7]利用休假式排队模型描述码头内部集卡和外部集卡的特征,建立了内外集卡协同服务的码头集卡预约优化模型.邵乾虔等[8]提出了码头与车队信息互联互通的码头集疏港联动预约模式.
通过对现有研究成果的梳理发现,目前针对码头堆场内场桥调度与集港预约份额分配的研究都是独立进行的.但两者是相互承接、相互关联的,场桥调度策略直接关系到整个集港过程的效率,而预约份额分配方案又决定了场桥的调度策略.因此,本文以整个决策期送箱集卡在闸口的排队等待时间、预约集港导致集港时段调整的集卡数及所有预约时段未完成的作业量所需的场桥作业时间最小为上层规划目标,以每个预约时段未完成作业量所需的场桥作业时间最小为下层规划目标,建立集装箱码头送箱集卡预约与场桥调度协同优化模型.
1 问题描述与模型假设
1.1 问题描述
预约集港即集装箱码头根据堆场的机力配备情况,设置各个集港时段的最大集港量(预约份额),港外堆场则根据码头公布的集港信息及自身运力情况在网上预约集港时段,并在预约的时段内送箱到港.送箱集卡到达码头闸口后随机选择1条闸口通道排队等待进港,闸口收箱员对出口箱及相关文件检验无误后指示外集卡到指定箱区等待场桥服务.为了充分利用场桥的作业能力,场桥在完成当前箱区较少的作业任务后需要转移到任务量较多的箱区.因此,码头可根据集港计划准确制定未来1天的场桥调度计划.
1.2 模型假设
(1)决策期为1天;
(2)用工作时间衡量场桥的工作能力,在不考虑设备故障的情况下,所有场桥各调度计划时段的工作能力是相同的;
(3)每个时段内每台场桥最多只能转场1次;
(4)为避免场桥间潜在的碰撞危险,同一箱区最多配备2台场桥;
(5)场桥移动的开始和结束时间都在同一时段内;
(6)码头闸口处可被视为N个M M 1型排队系统,N为闸口通道个数.
2 模型构建
2.1 模型参数与变量定义
(1)输入参数.
p为时段编号,将1天分成P个预约时段,p=1,2,…,P;t为将每个时段p分成σ个小的时间间隔,并以时间间隔中的某个时刻t(t=1,2,…,Pσ)代表该时间间隔;n为闸口通道的编号,n=1,2,…,N;i为出口箱区的编号,i=1,2,…,I;j为服务于出口箱区的场桥编号,j=1,2,…,J;λi,p为偏好在时段p到港并将集装箱送到箱区i的集卡数;C为单台场桥1个时段内的作业能力,;τ为场桥完成1次操作所需要的平均时间;v为船舶编号,根据截载时间由早到晚依次编号,v=1,2,…,V;tv为船舶v的截载时间;ci,v为到达箱区i给船舶v送箱的集卡数;Ti,j,p为时段p场桥 j移动至箱区i所需的时间;ri,p为时段p开始之初箱区i配备的场桥数.
(2)衍生变量.为t时刻通道n处集卡平均排队长度;为t时刻通道n处集卡到达率;为t时刻通道n处集卡离开率;为t时刻通道n的利用率;为t时刻通道n的服务率;为时段p集卡在通道n的平均等待时间;为时段p不需要增加场桥的箱区(即场桥作业能力大于等于作业量)集合;为时段p无法再增加场桥的箱区(即场桥作业能力小于作业量,且已配置2台场桥)集合;为时段p需要增加场桥的箱区(即场桥作业能力小于作业量,且配置的场桥数小于2)集合;Rp为时段p可移动的场桥集合;为场桥调度前,时段p箱区i未完成作业量所需的场桥作业时间;为场桥调度后,时段p箱区i富余的场桥作业时间;Fi,p为时段p结束时箱区i未完成作业量所需的场桥作业时间;为时段p场桥j(j∈ Rp)被移动前富余的作业时间;为时段p场桥j(j∈ Rp)富余的作业时间不足以移动到的箱区集合,且.
(3)决策变量.
时段p箱区i的预约份额;xi,j,p为0-1变量,时段p场桥j移动至箱区i时,xi,j,p=1,否则xi,j,p=0.
2.2 上层规划模型
目标函数:

约束条件:


式(1)为目标函数,以整个决策期集卡在闸口的排队等待时间、预约导致集港时段调整的集卡数及所有时段未完成的作业量所需的场桥作业时间总和最小为目标,Fp由下层规划求得;式(2)表示预约前后集卡到达量守恒;式(3)表示将集卡到达量转化为较小时间间隔的集卡到达率;式(4)表示排队队长的变化等于到达率减去离开率;式(5)表示t时刻通道i处的集卡离开率;式(6)表示t时刻通道i的利用率;式(7)表示集卡在闸口的平均等待时间;式(8)表示预约份额要保障集卡在相应船舶截载前运抵码头;式(9)表示预约份额非负.
2.3 下层规划模型
目标函数:
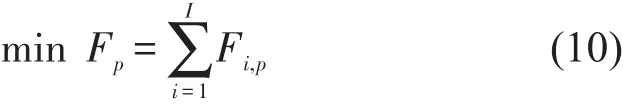
约束条件:

式(10)为目标函数,以时段p未完成作业量所需的场桥作业时间最小为目标;式(11)~式(13)表示箱区i不需要或无法增加场桥,场桥j不可移动或富余的作业时间不足以移动到箱区i时,场桥j不能调往箱区i;式(14)表示场桥每个时段最多移动1次;式(15)表示时段p结束时箱区i未完成的作业量所需的场桥作业时间;式(16)表示1个箱区最多配备2台场桥;式(17)表示非负约束.
下层规划模型中的变量,以及箱区和场桥(Rp)的分类均由λy*i,p及当前箱区配备的场桥数确定.集装箱码头的实际生产运营中箱区的作业任务并无法在各个时段开始时就全部到达,即直至时段结束场桥都要服务于该箱区.因此,上述变量及箱区、场桥分类的确定方法如下.
(1),且ri,p=2时,箱区,该箱区的场桥
(2),且ri,p<2时,箱区i∈BSp,该箱区的场桥
(3)时,箱区i∈BpE,该箱区的场桥.
(4)时,箱区,但箱区i现有场桥的分类需进一步讨论:
①时,场桥;ri,p=2时,,且场桥j2在箱区i服务Oj2后空闲,满足的箱区
②时,场桥j∈Rp,,满足的箱区;.时,场桥,,满足的箱区,满足的箱区时,,满足的箱区
3 算法设计
二层规划问题的嵌套本性导致其可行解集不再具备凸性和闭性,且非处处可微,从而阻碍了梯度法、最小二乘等利用导数的优化算法的使用.而遗传算法对函数的可导性没有要求,加之其全局收敛性、隐含的并行性和较强的鲁棒性,使其能够有效求解结构复杂的二层规划问题.因此,本文设计了并行遗传算法(Parallel Genetic Algorithm,PGA)对模型进行求解,算法流程如图1所示.

图1 PGA求解二层规划模型的流程图Fig.1 The flow chart of PGA for bi-level programming
算法步骤:
Step 1编码与初始种群.染色体的基因依次为各箱区各预约时段的集卡到达量,即H台服务器分别在式(2)和式(8)的约束下,随机生成一定数量的个体.
Step 2计算适应度.鉴于本文是求解目标函数的最小值,取作为适应度函数.其中,M为足够大的整数.
Step 3选择操作.使用轮盘赌选择算子,对子种群中的染色体进行选择.
Step 4交叉操作.本文采用随机错位算术交叉算子对父代进行交叉操作生成子代.为满足式(2)的约束,仅对表示同一箱区的部分染色体进行交叉.同时,为了满足式(8)的约束,根据船舶的截载时间设置交叉点,对每两个相邻交叉点间的基因进行随机配对.然后,对配对的2个等位基因g1i和g2j进行式(18)的算术运算.
Step 5 变异操作.为保证变异后仍满足式(2)的约束,随机选择1条染色体中同一箱区的2个基因gim和gin(n>m)进行变异.为了满足式(8)的约束,gim变异的下限如式(19)所示,变异的上限为随机产生范围内的整数δ,则变异后,具体操作过程如图3所示.

式中:β为一个常数,取0.5.
新产生的染色体各有A个非整数基因,将染色体1的前A2个非整数基因向上取整,后A2个非整数基因向下取整,染色体2中对应的基因位进行相反操作,如图2所示.t1=8,t2=20,t3=24,ci,v取值如表1所示.场桥在各箱区间移动所需要的时间如表2所示.

图2 随机错位算术交叉操作示意图Fig.2 Schematic diagram of random dislocation arithmetic crossover
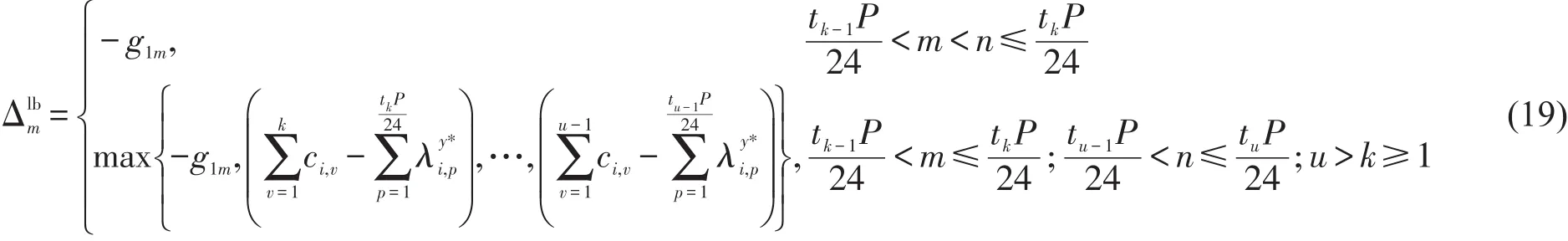

图3 变异操作示意图Fig.3 Schematic diagram of mutation
Step 6子种群的迁移.当G/GE=0时,用子种群中适应度值最大的前NE个个体替换掉相邻子种群中适应度值最小的NE个个体.
Step 7当算法的进化代数达到最大进化代数,算法终止.
4 算例分析
4.1 算例描述
以天津东方海陆集装箱码头的实际数据进行实例分析,该集装箱码头拥有2条集港通道,15个出口箱区,10台场桥服务出口箱区,如图4所示.模型参数取值为:,

表1 箱区集卡到达信息Table 1 The arrival information of trucks for export containers in each block

图4 决策开始前箱区的场桥配置情况Fig.4 The allocation of cranes at the beginning of the decision-making horizon

表2 场桥在各箱区间的移动时间Table 2 Crane traveling time between blocks (min)
4.2 运算结果
利用Matlabr2010b编写算法程序,并在PC(CPU:四核酷睿3.2 GHz;内存:4 G)上运行.本文设计的并行遗传算法的收敛过程如图5所示,迭代5 000次后算法终止,共耗时3 971.11 s,目标函数值收敛于2 922.3.
预约前后集卡到达量和平均等待时间如图6所示,实施预约集港前,集卡在闸口的平均等待时间为5.553 min,最长等待时间为12.336 min;实施预约集港后,集卡在闸口的平均等待时间和最长等待时间分别降至4.309 min和4.820 min.结果表明,预约集港有削峰平谷的作用,能有效缓解送箱集卡在闸口处长时间排队等待的问题.根据预约集港下的集卡到达量得到场桥调度方案如图7所示.

图5 PGA的收敛过程Fig.5 Convergence procedure of CPGA

图6 预约前后集卡到达量和平均等待时间Fig.6 Number of trucks arrival at each block and waiting time before and after appointment
4.3 不同优化策略的对比与分析
为了与本文提出协同优化模型进行对比,同时,对同一算例的独立决策策略进行数值实验,即先优化集港预约份额,根据得到的最优集港预约份额分配方案优化场桥的调度,运算结果如表3所示.可见,两种优化策略都能有效降低集卡在闸口的等待时间,且独立决策下集港时段被迫改变的集卡数更少.但是,由于集港预约份额优化过程中没有考虑场桥调度,导致独立优化策略下整个决策期所有箱区未完成作业量要远大于协同优化策略.对比结果表明,本文建立的模型能够实现送箱集卡预约与场桥调度的协同优化,更大限度提高集港过程中集装箱码头闸口和堆场的整体作业效率.

图7 场桥调度方案Fig.7 The crane deployment plan

表3 不同优化策略的实验结果Table 3 Experimental results of different optimization strategies
5 结 论
针对送箱集卡随机到港引起的场桥作业不均衡,以及高峰时段场桥资源紧缺、集装箱码头拥堵等问题,构建送箱集卡预约与场桥调度协同优化的二层规划模型,并设计PGA算法求解模型.算例分析验证了本文所建优化模型的正确性和所设计算法的有效性,结果表明:
(1)实施预约集港后,送箱集卡在闸口的最长等待时间由12.336 min缩短为4.820 min,可见,实施预约集港能够显著降低送箱集卡在闸口的排队等待时间;
(2)独立决策策略下所有箱区未完成作业量所需的场桥作业时间为345 min,而协同优化策略下没有未完成作业量,可见,协同优化比独立决策更有利于提高送箱过程中集装箱码头闸口和堆场的整体作业效率.
但本文还存在不足,如每个时段的场桥调度优化都是独立进行的,没有考虑场桥的动态调度问题,未来需进一步研究场桥动态调度与集卡预约份额协同优化,以及其他高效启发式算法的应用.
[1]ZHANG C,WAN Y,LIU J,et al.Dynamic crane deployment in container storage yards[J].Transportation Research Part B:Methodological,2002,36(6):537-555.
[2]LINN R,LIU J,WAN Y,et al.Rubber tired gantry crane deployment for container yard operation[J].Computers&Industrial Engineering,2003,45(3):429-442.
[3]李建忠.码头堆场龙门起重机动态配置优化模型[J].交通运输工程学报,2005,5(1):70-74.[LI J Z.Crane dynamic deployment model of container storage yard[J].Journal of Traffic and Transportation Engineering,2005,5(1):70-74.]
[4]吴达,冉祥辰.集装箱预约集港的探索与实践[J].港口经济,2012(3):5-9.[WU D,RAN X C.Exploration and practice of export container appointment in container terminals[J].Port Economy,2012(3):5-9.]
[5]ZHANG X,ZENG Q,CHEN W.Optimization model for truck appointment in container terminals[J].Procedia-Social and Behavioral Sciences,2013,96(6):1938-1947.
[6]CHEN G,GOVINDAN K,GOLIAS M M.Reducing truck emissions at container terminals in a low carbon economy:Proposal of a queueing-based bi-objective model for optimizing truck arrival pattern[J].Transportation Research Part E,2013,55(6):3-22.
[7]曾庆成,张笑菊,张倩.内外集卡协同服务的码头集卡预约优化模型[J].交通运输工程学报,2016,16(1):115-122.[ZENG Q C,ZHANG X J,ZHANG Q.Optimization model of terminal container truck appointment based on coordinated service of inner and outercontainertrucks[J].JournalofTraffic and Transportation Engineering,2016,16(1):115-122.]
[8]邵乾虔,靳志宏,邢磊.基于联动预约模式的集装箱码头集疏港仿真优化[J].交通运输系统工程与信息,2016,16(4):217-224.[SHAO Q Q,JIN Z H,XING L.Simulation optimization of consolidation and configuration in container terminals based on cooperative appointment[J].Journal of Transportation Systems Engineering and Information Technology,2016,16(4):217-224.]
