基于粗糙集聚类算法的铁路通道客运市场细分
2018-06-29李海军李引珍朱昌锋马昌喜
李海军,李引珍,周 鹏,朱昌锋,马昌喜
(兰州交通大学交通运输学院,兰州730070)
0 引 言
细分铁路通道客运市场有助于铁路运输企业快速高效地确定目标市场,对旅客出行选择研究、设计客运产品、客流分配研究等具有积极意义.
针对铁路客运市场的细分问题,大部分文献是按照旅客不同的人口统计特征和出行属性来细分市场[1-2].这样人为划分标准,不能很好地反映客观情况,文献通过因子分析法[3]、经典K-means聚类算法[4]、混合回归模型[5]等聚类算法得到比较客观的客运市场细分结果.此外,文献[6]引入潜在类别分析理论对客票数据进行研究,寻找潜在的旅客细分市场;文献[7]通过凝聚法合并铁路旅客出行属性变量,利用近邻传播算法对旅客进行样本聚类.但铁路旅客自身属性和出行特征属性是高维的,包含大量的信息,并且有些属性是冗余的,这就要求首先对数据进行简化降维,在此基础上,通过高效的聚类算法客观地细分铁路旅客市场.
粗糙集理论无须提供所处理数据之外的任何先验信息的特点,为研究铁路通道客运市场细分问题提供了新的思路.本文将铁路旅客出行方式选择影响因素作为个体描述的变量,采用粗糙集理论的属性约简算法对变量进行降维,然后通过改进的粗糙集属性权重的K-means聚类算法对旅客样本进行细分,从而为旅客出行选择研究等奠定理论基础.
基于粗糙集聚类算法的铁路通道客运市场细分流程,如图1所示.

图1 铁路通道旅客出行知识获取流程图Fig.1 Knowledge acquisition flow chart of passenger travel in railway corridor
1 调查设计与数据采集
铁路通道旅客出行主要受旅客自身属性、出行特征和运输方式特征的影响,其类别的细分应包含以下变量:旅客的性别、年龄、职业、月收入、出行目的、旅费来源等基本信息,以及旅客选择不同出行方式的满意度(包括票价、旅行时间、便捷程度、准时性、舒适度、安全性6个维度).
本文以行为调查(RP)和意向性调查(SP)相结合的方式进行问卷调查,在宝鸡—兰州铁路通道,采用跟车问卷调查与定点调查相结合的方法进行抽样调查.共发放1 500份问卷,回收1 363份有效问卷,回收率为90.8%.样本数据具体描述如表1所示.

表1 铁路通道旅客出行选择决策Table 1 Decision table of passenger travel choice in railway corridor
表1中各变量的取值方法如下.
性别:0=男,1=女.
旅费:0=公费,1=自费.
年龄:0=(0,18)岁,1=[18,30)岁,2=[30,40)岁,3=[40,50)岁,4=[50,60)岁,5=60岁及以上.
职业:0=国企及事业单位人员,1=公务员,2=个体经营者,3=离退休人员,4=公司职员,5=工人,6=农民,7=学生,8=军人,9=其他.
收入:0=(0,1 500]元,1=(1 500,4 000]元,2=(4 000,6 000]元,3=(6 000,8 000]元,4=(8 000,10 000]元,5=10 000元以上.
出行目的:0=公务出差,1=旅游,2=探亲访友,3=购物,4=务工,5=上学,6=其他.
教育程度:0=初中以下,1=高中,2=本科,3=研究生.
票价、旅行时间、便捷程度、准时性、舒适性、安全性:0=很不满意,1=比较不满意,2=一般满意,3=比较满意,4=很满意.
出行选择:0=高速铁路,1=普通铁路.
2 基于粗糙集的铁路通道旅客出行属性约简及权重计算
2.1 粗糙集理论概述[8]
定义1知识的约简.给定一个知识库K=(U,S)和知识库上的一族等价关系P⊆S,对任意的G⊆P,若G是独立的,且IND(G)=IND(P),则称G是P的一个约简,记为G∈RED(P),其中,RED(P)表示P的全体约简集合.
定义2决策表.称四元组DT=(U,C∪D,V,f)是1个决策表,其中,U为对象的非空有限集合,称为论域,U={x1,x2,…,xn};C∪D中,C为条件属性集,C={a|a∈C},D为决策属性集,D={d|d∈D},且C⋂D=∅,C≠∅,D≠∅;V表示信息函数f的值域,V=⋃Vα(∀α∈C⋃D);f表示决策表的信息函数,f={fα|fα:U → Vα,∀α ∈ C ⋃ D}.
定义3令C、D⊆A,定义两个属性集C与D之间的依赖程度γc(C,D)为
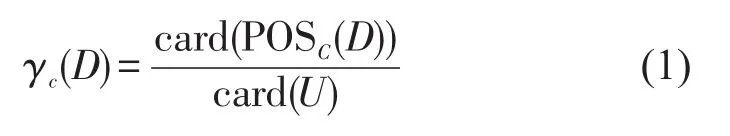
式中:POSC(D)为D的C正域,即U中所有根据分类U/C的信息可以准确划分到关系D的等价类中去的对象集合;card[]表示集合的基数,即集合中元素的个数.
定义4四元组DT=(U,C∪D,V,f)是1个决策表,根据属性依赖度的定义,任意属性c(c∈C)在C中对D的重要性定义为
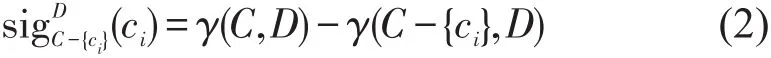
其值越大,说明属性c关于属性集C就越重要.
定义5根据式(2)归一化所有条件属性的重要度,可得条件属性ci的权重公式为
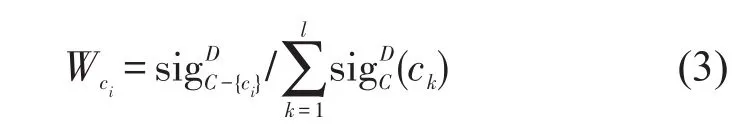
2.2 粗糙集属性约简及权重
由定义2可知,可将宝兰铁路通道旅客出行方式选择调查表定义为决策表DT=(U,C∪D,V,f),其中:U为出行选择的所有旅客样本;C为条件属性的非空有限集合,即出行选择中所有影响旅客出行选择的因素;D为决策属性,表示旅客选择的铁路出行方式,高铁或普铁;V为信息函数f的值域,每个属性的取值不同,该模型中,所有的值域均为离散型.
对上述决策表,通过Mean Completer算法进行数据表补齐的预处理,采用遗传算法进行属性约简,结果为:{性别,年龄,职业,收入,出行目的,教育程度,票价,旅行时间,便捷程度,准时性,舒适度,安全性}.
可见,只有“旅费来源”这一个属性是冗余属性,根据属性重要度计算公式,分别对这12个影响因素根据式(2)计算重要度为{0.012,0.015,0.025,0.009,0.025,0.011,0.012,0.011,0.007,0.005,0.004,0.004};根据式(3)计算各关键属性的权重为{0.085 714,0.107 143,0.178 571,0.064 286,0.178 571,0.078571,0.085714,0.078571,0.050000,0.035 714,0.028 571,0.028 571}.
3 基于粗糙属性重要度的改进K-means聚类算法
经典的K-means聚类算法,将距离准则函数中的每个属性同等对待,这会造成不相关属性的误导,即出现“维数陷阱”.通过粗糙集确定属性权重,使得不同的属性在聚类中起不同的作用,能客观解决这个问题.
3.1 基于属性加权距离、密度的初始化中心点算法
3.1.1 基本定义
定义6 加权欧式距离.通过粗糙集属性重要度赋予不同属性权值,得到xi与cj之间的欧式距离为

式中:wl表示属性的权重.
定义7 聚类对象的密度.已知样本的数据集U={xi,i=1,2,…,n},样本的属性权重集为W={wl,l=1,2,…,m},其中对象xi处的密度函数为
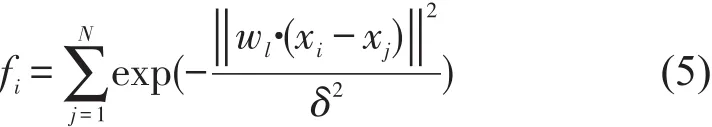
定义8聚类对象的邻域半径.
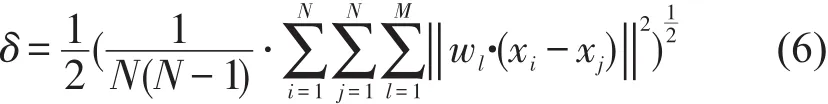
3.1.2 算法描述
基本思想:首先,根据粗糙集属性约简和属性重要度定义,得到约简后不同属性的权重,避免“维数陷阱”;然后,在样本的数据集U中选择密度最大的点作为第1个初始中心,同时U中删去该点及邻域内的所有对象,同样方法确定第2个中心点,循环执行.
算法1
Step 1由定义7计算所有对象密度,得到密度点集合D,初始化中心集为空,M={∅}.
Step 2选择密度最大的样本对象.xmax=max{xi|xi∈D,i=1,2,…,N },作为第1个初始中心点,加到中心点集M中,M=⋃{xmax}.并根据定义8,从样本集中删去xmax及邻域对象.
Step 3重复执行Step2.直到选取了K个初始中心点.
Step 4输出K初始中心点集,结束.
3.2 基于属性加权距离的K-means聚类算法
3.2.1 基本定义
对数据进行聚类分析之后,聚类结果的优劣还需通过内、外部度量的准则函数加以分析.
定义9类内距离.类内每一个样本数据到它们所属中心的距离

定义10类间距离.不同聚类中心间的距离.
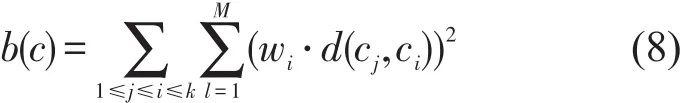
显然,要使聚类结果中同一类内的数据尽可能相似,而不同类之间的数据尽可能差异显著,即类内距离应该越小,类间距离应该越大.汪中等[9]提出了类内差异和类间差异平方和的二次方根作为评价函数,以最小的评价函数对应的K值作为最优聚类数,虽然此方法能找到最优的聚类数,但当数据量较大时,得到的聚类数比较多,这与实际应用不符合.因此本文提出了用类内距离和类间距离的比值作为评价函数来评价聚类效果.
定义11评价函数.类内距离同类间距离的比值为

当J(c,k)值收敛时,得到最优聚类.
3.2 .2算法描述
结合文献[9-10]的思想,基于本文算法1进一步提出基于粗糙属性加权距离的K-means聚类算法.文献[11]已证明,整数K的取值范围为[1,n],n为数据对象数.算法2从[1,n]循环执行,并记录均衡评价函数值及其对应的K值.评价函数值最小的K值,即为最优聚类数目.
算法2
输入:包括n个样本数据的数据集,样本数据各属性的粗糙重要度wl.
输出:最优K值和对应的聚类结果.
Step 1
Step 1.1调用算法1确定K个初始聚类中心;
Step 1.2计算聚类中心的平均值,将每个数据对象赋给距离最近的聚类中心,根据定义6确定数据对象到聚类中心的距离;
Step 1.3更新簇的平均值;
Step 1.4根据式(9)计算评价函数J(c,k),直到其收敛为止,否则转入Step1.2.
Step 2根据记录的J值,找出J值收敛时对应的K值,即为最优聚类数目.
3.3 基于粗糙属性重要度的K-means聚类算法
由3.1节和3.2节可知,本文提出的基于粗糙属性重要度的K-means聚类算法,首先通过粗糙集约简算法对数据集进行属性约简和属性重要度计算,然后由算法1和算法2得到聚类结果,具体步骤如下:
输入:包含n个对象的d维数据集.
输出:K个聚类.
Step 1由本文的约简算法对d维数据集进行属性约简.
Step 2生成包含n个对象的属性为K(K<d)个的数据集.
Step 3计算K个属性对应的重要度wi(i=1,2,…,k).
Step 4调用算法2,得到最优聚类数目和聚类结果.
3.4 算法的仿真实验
为了验证算法的有效性和正确性,本文采用UCI数据库中的Iris、Wine和Soybean这3个数据集,分别运行传统K-means算法、粗糙K-均值算法[12]、文献[13]的基于密度加权的粗糙K-均值聚类改进算法,以及本文提出的基于粗糙属性重要度的K-means算法进行仿真实验,结果汇总如表2所示.

表2 Iris、Wine、Soybean数据集的实验结果Table 2 Experimental result for Iris、Wine&Soybean
从聚类实验结果可以看出,本文改进算法的准确率较高且稳定,对实际数据的聚类效果更好,可以用于铁路客运市场细分研究.
4 宝兰铁路通道客运市场细分
根据2.2节得到的属性权重,执行本文基于粗糙属性重要度的K-means聚类算法,得到聚类数K与评价函数J(c,k)的收敛趋势图,如图2所示.
可见,当K=6时,评价函数J(c,k)趋于收敛,宝兰铁路通道客运市场可以细分为6类.
经过对各细分子市场中旅客的个人属性、出行影响因素重视度及主要席别选择的统计分析,可以总结出不同子市场的主要特征,如表3所示.
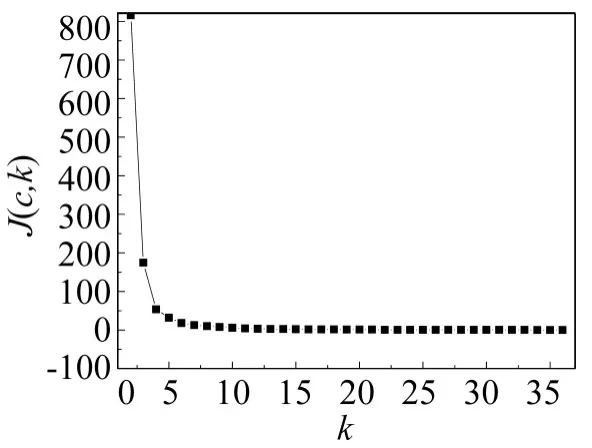
图2 宝兰铁路通道旅客市场细分聚类算法评价函数收敛图Fig.2 Cluster algorithm convergency diagram for passenger transport market segmentation

表3 各细分市场的主要差异Table 3 Difference table of passenger transport segmentation market
通过对各子市场的旅客调查分析发现,安全性是每个子市场最为重视的因素,除安全性以外,子市场1的旅客最重视的是票价高低,而且大部分旅客的出行目的是务工;子市场2最重视舒适度,旅游探亲占了大部分;子市场3以青年学生为主力,大部分的收入低,以上学为主;子市场4主要是公务员和国企员工,出行目的主要是出差;子市场5最看重票价,以工人、农民、学生为主,主要出行目的是探亲;子市场6最重视时刻表,以个体经营者为主.综上所述,将上述6个子市场根据旅客出行特征分别命名为:经济务工型、休闲舒适型、低端年轻型、高端公务型、经济探亲型、商务时间型.市场细分的结果可为铁路部门设计个性化的客运产品提供依据.
5 结论
本文通过分析宝兰铁路通道旅客出行方式选择调查数据的特征,提出了基于粗糙属性重要度的K-means聚类算法,将铁路通道客运市场细分为6类子市场:经济务工型、休闲舒适型、低端年轻型、高端公务型、经济探亲型、商务时间型.今后将对铁路通道客运细分子市场的客流分担,以及针对不同客运细分子市场的差异化的高铁和普铁客运产品设计,做进一步研究.
[1]冯运卿,李雪梅,李学伟.基于粗糙集的复合属性铁路旅客出行决策影响因素分析与权重计算[J].铁道学报,2014(9):1-9.[FENG Y Q,LI X M,LI X W.Analysis of influence factors an weighting based on rough sets and the railway passenger travel decisionmaking[J].Journal of the China Railway Society,2014(9):1-9.]
[2]吴文娴.铁路通道内客流分担率及客运组织策略研究[J].中国铁道科学,2011,32(2):126-130.[WU W X.The organization strategy research of passenger flow and the share rate of passenger transport railway channels[J].Journal of China Railway Science,2011,32(2):126-130.]
[3]蒋学斌.高速铁路客运市场细分与差异化营销策略 [J].中 国 铁 路,2014(2):6-8.[JIANG X B.Segmentation of high-speed railway passenger transport market and differentiated marketing strategy[J].China Railway,2014(2):6-8.]
[4]杜巍,赵春荣,黄伟建.改进的K-means聚类算法在客户细分中的应用研究[J].河北经贸大学学报,2014,35(1):118-121.[DU W,ZHAO C R,HUANG W J.Research on application of improved K-means clustering algorithm in customer segmentation[J].Journal of Hebei University of Economics and Business,2014,35(1):118-121.]
[5]钱丙益,帅斌,陈崇双,等.基于混合回归模型的客运专线旅客市场细分研究[J].铁道运输与经济,2014,36(1):60-65.[QIAN B Y,SHUAI B,CHEN C S,et al.Study on subdivision of DPL passenger market based on mixed regression model[J].RailwayTransportand Economy,2014,36(1):60-65.]
[6]张永超.基于RoughSet高速铁路市场细分研究[D].成都:西南交通大学,2014.[ZHANG Y C.Research on high-speed railway passenger-marketsegmentation based on rough set[D].Chengdu:Southwest Jiaotong University,2014.]
[7]吕红霞,王文宪,蒲松,等.基于聚类分析的铁路出行旅客类别划分[J].交通运输系统工程与信息,2016,16(1):129-134.[LV H X,WANG W X,PU S,et al.Classification of railway passengers based on cluster analysis[J]. Journal of Transportation Systems Engineering and Information,2016,16(1):129-134.]
[8]苗夺谦,李道国.粗糙集理论、算法与应用[M].北京:清华大学出版社,2008.[MIAO D Q,LI D G.Rough set theory,algorithm and application[M].Beijing:Tsinghua University Press,2008.]
[9]汪中,刘贵全,陈恩红.一种优化初始中心点的K-means算法[J].模式识别与人工智能,2009,22(2):299-304.[WANG Z,LIU G Q,CHEN E H.A K-means algorithm based on optimized initial center points[J]. Pattern Recognition and Artificial Intelligence,2009,22(2):299-304.]
[10]姚跃华,史秀岭.一种优化初始中心的K-means粗糙聚类算法[J].计算机工程与应用,2010,46(34):126-128.[YAO Y H,SHI X L.K-means rough clustering algorithm based on optimized initial center[J].Computer Engineering and Applications,2010,46(34):126-128.]
[11]杨善林,李永森,胡笑旋,等.K-means算法中的K值优化问题研究[J].系统工程理论与实践,2006,26(2):97-101.[YANG S L,LI Y S,HU X X,et al.Optimization study on K value of K-means algorithm[J].System Engineering Theory and Practice,2006,26(2):97-101.]
[12]聂映,陈福集.一种基于粗糙集的K-means聚类算法[J].武汉大学学报(工学版),2011,44(2):257-260.[NIE Y,CHEN F J.Research of K-means clustering algorithm based on rough set[J].Journal of Wuhan University(Engineering Science),2011,44(2):257-260.]
[13]郑超,苗夺谦,王睿智.基于密度加权的粗糙K-均值聚类改进算法[J].计算机科学,2009,36(3):220-222.[ZHENG C,MIAO D Q,WANG R Z.Improved rough K-means clustering algorithm with weight based on density[J].Computer Science,2009,36(3):220-222.]
