基于复杂网络同步城市快速路协调控制研究

庞明宝，刁化尧，赵冰心，黄玉满

(河北工业大学土木与交通学院，天津300401)

0 引 言

协调控制是连续交通流道路抑制拥堵、提高通行效率的最有效措施，特别是上下班高峰需求较大时段的城市快速路[1-2].协调控制分为匝道与主线间、多入口匝道间、快速路与其他道路间等多种方式.其中，多入口匝道协调效果最明显，其控制方法和算法分为：建立在OD预测基础上采用非线性规划模型优化求解的一体化匝道控制及扩展的双层规划算法，该方法存在模型复杂、求解繁琐，依赖于预测精度、不具备反馈机制，难于大规模网络应用等不足；基于现代控制、智能控制的反馈控制方法，也存在计算量大、难于大规模网络应用等不足；基于经验包括 Helper、Bottleneck、CORDIN、Zone、Swarm等算法在内的启发式协调控制方法[1]，技术复杂性低、可实施性好，但存在依赖经验、难于应用于大规模网络等问题；大系统分解协调算法，可应用于大规模网络，但核心在分层递解协调算法.同时这些研究均建立在已确定出协调控制信号施加范围基础上，均不涉及复杂网络系统理论及其同步控制.

研究已经证明道路交通是复杂网络系统，而利用复杂网络理论及同步等解决交通问题是一项新课题[3].在城市快速路协调控制方面，其目标是当系统出现拥堵即接近临界密度时通过一些匝道的协调调节，使密度与期望密度的偏差最小，实现系统有序达到抑制交通拥堵的目的，其与复杂网络同步的目标相一致.同时复杂网络的牵制控制[4]，即部分节点实施控制与协调控制中在大多范围内施加协调控制信号在思想上是相一致的.这是因为城市快速路的相对封闭性使拥堵传播的速度非常快，上游受影响路段车辆可供选择的路径非常有限，影响范围会更广，若对拥堵不予理睬或缩小控制范围，车辆不能迅速通过，可能造成长时间大范围的拥堵；而若扩大管控范围，使很多车辆转移到城市一般道路上，造成这些本来已拥挤的道路更加拥堵，也不是交通管理的目的.若能采用牵制控制的思想方法确定出对哪些匝道施加控制信号，将为协调控制取得最佳效果提供理论依据.基于此，本文以城市快速路为研究对象，采用元胞传输模型(Cell Transmission Model,CTM)建立节点耦合的复杂网络模型，以同步为目标设计多入口匝道协调控制器，推导系统稳定性条件，通过具体应用仿真实验予以验证.

1 城市快速路节点耦合模型

1.1 城市快速路CTM

采用CTM来映射研究对象——城市快速路的非线性交通流过程[5]，各参数和变量为：f(m-1)m(t)为t时从元胞m-1流入m的车辆数，sm(t)和rm(t)分别为元胞m在t时发送和接收能力(veh/h)；vf为自由流速度，km(t)为元胞m在t时密度，Qm为元胞m通行能力，ω为反向波速，kJ为拥堵密度；fpm(t)为t时从入口p流入主线元胞m的车辆数，fp(m-1)m(t)为t时进入元胞m的总车辆数，α为合并系数，med表示取中间值；fm(m+1)o(t)为t时流出元胞m的总车辆数，β为分离系数，fmo(t)为t时从元胞m流入相连出口元胞o的车辆.各路段连接按CTM要求分为无出入口连接的基本段、有入口融合连接的合流段和有出口分离连接的分流段3种模式，如图1所示，对于立交桥可看作是3种模式的组合.动力学模型分别为：

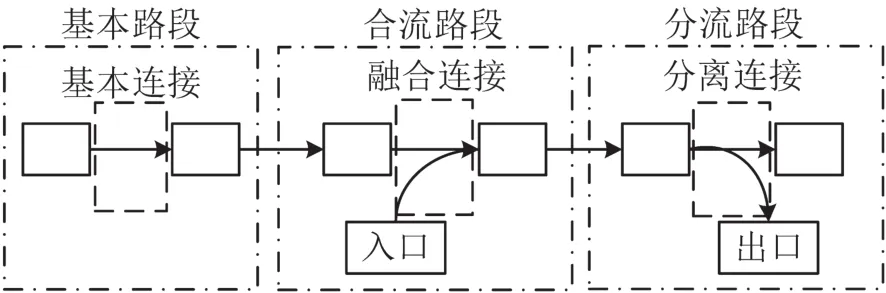
图1 3种连接路段示意图Fig.1 Transmission relation in three types of connection

(1)基本路段连接间为

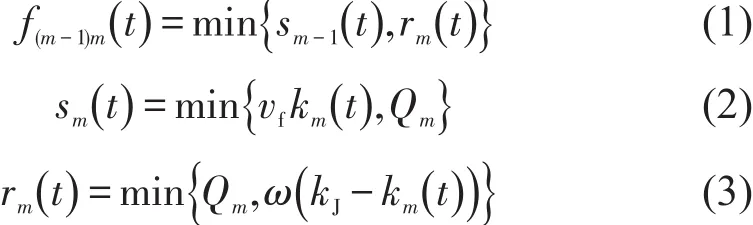
(2)融合连接间为

(3)分离连接间为

1.2 快速路节点耦合模型

将快速路看成由若干节点组成的大系统，具体节点结构如图2所示.图2为含主线、入口匝道和出口匝道元胞组成的标准形式，对非标准(没有出口或入口元胞)的节点，将其入口流量或出口流量设置为0；对立交桥分解后的节点，考虑到出入口距离较近且有交织区的存在，其入口汇入和出口分离比例要比正常出入口小一些.

图2 节点示意图Fig.2 Sketch diagram of node

如图2所示，节点i内部主线元胞m状态转移为：

(1)从入口p流入主线min{s i,p(t),αri,m(t)}.其中，si,p(t)为节点i主线元胞m相连的入口元胞p在t时的发送能力，当没有入口相连时为0；ri,m(t)为元胞m的接收能力.

(2)从主线元胞出口流出βsi,m(t).其中，si,m(t)为元胞m发送能力，当没有与之相连的出口时为0；ki,m(t)为元胞m密度.

在不考虑耦合作用(即无主线上的流入流出量)下i节点状态方程为

式中：ε为采样周期时长(s)；li,m为元胞m长度(km).

式(10)表示节点i的主线元胞m在下一时刻密度为当前时刻密度加上流入主线的密度减去流出主线的密度.

定义快速路主线元胞i,j(i,j=1,2,…,N)间，若相连，则gij为1；否则，为0.定义，则其邻接矩阵为

根据节点间位置关系，节点间状态变量的耦合函数矩阵为

得到节点耦合模型

式中：f为式(10)；a为耦合强度；N为节点数.

式(13)表示节点i主线元胞m在t+1时的密度等于上一时刻密度加上从上游节点流入车辆增加的密度，再减去从本节点流出车辆减少的密度.

2 基于复杂网络同步的城市快速路协调控制器设计

2.1 协调控制策略及控制器算法

依然采用期望密度ρd(临界密度ρc负邻域)作为控制信号施加条件，具体施加策略为：当城市快速路部分路段—节点出现密度大于ρd时，先通过协调控制器计算施加控制信号范围——入口匝道的数量c；考虑到城市快速路的特点，具体信号施加的匝道为拥堵节点上游最近的c个；再计算匝道调节量，然后施加到确定后的匝道中.当拥堵消散，即这些节点密度小于ρd时若干步，再取消协调控制信号.

考虑到当主线部分节点出现拥堵时它们的密度较大，其上游节点可发送的车辆数完全由下游能容纳车辆数来决定，故式(11)可写成

其耦合强度和邻接矩阵转化为

对式(14)所述网络，当t→∞时，有，就称网络式(14)达到同步状态，其满足

为使网络达到同步状态，需对网络中的部分节点施加控制，即通过对部分入口匝道施加匝道调节信号.设选择前c个节点作为该牵制控制的被控节点，则这些被控节点的状态方程为

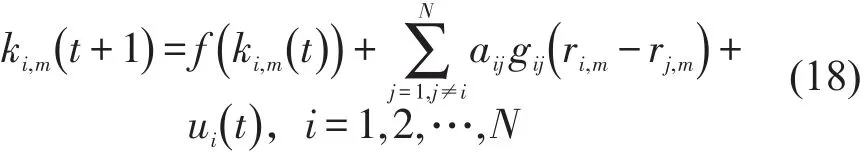
式中：ui(t)为节点i中主线元胞密度调节变化值，由流量调节值转化过来，即

当i=1,2,…,c时，di＞0；当i=c+1,c+2,…,N时，有di=0.同时考虑到部分节点需求低于式(19)计算结果的情况，此时取值为

2.2 同步稳定性分析与控制器参数确定

欲使式(11)和式(14)描述的城市快速路达到同步状态，必寻找合适的反馈增益阵D.定义为

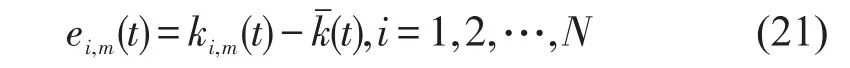
则系统的同步误差为

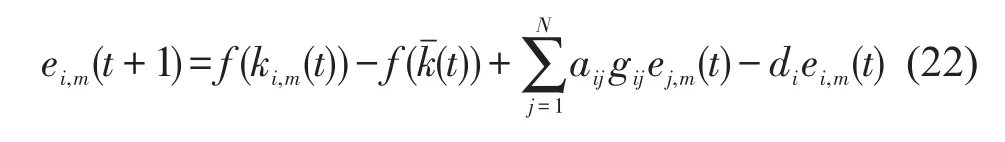
如果此误差网络能够逐渐稳定，则系统能达到全局同步.做出如下假设：

假设1[6]存在1个常数θ，使式(18)所述网络中的非线性函数f(ki,m(t))满足

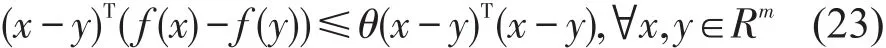
引理1[7]假设Q(x)=QT(x)、R(x)=RT(x)，对于给定的线性矩阵不等式式(24)与式(25)的条件之一等价.

定理1如果矩阵满足式(26)，则式(18)所述网络达到同步状态.其中D=diag( )d1,d2,…,dc,0,…,0.

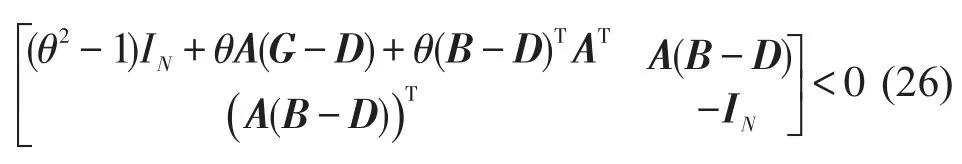
证明：考虑Lyapunov函数，即

由假设 1 可知，f(xi(t))-f((t))≤ θ(xi(t)-(t))，因此该函数可放缩为

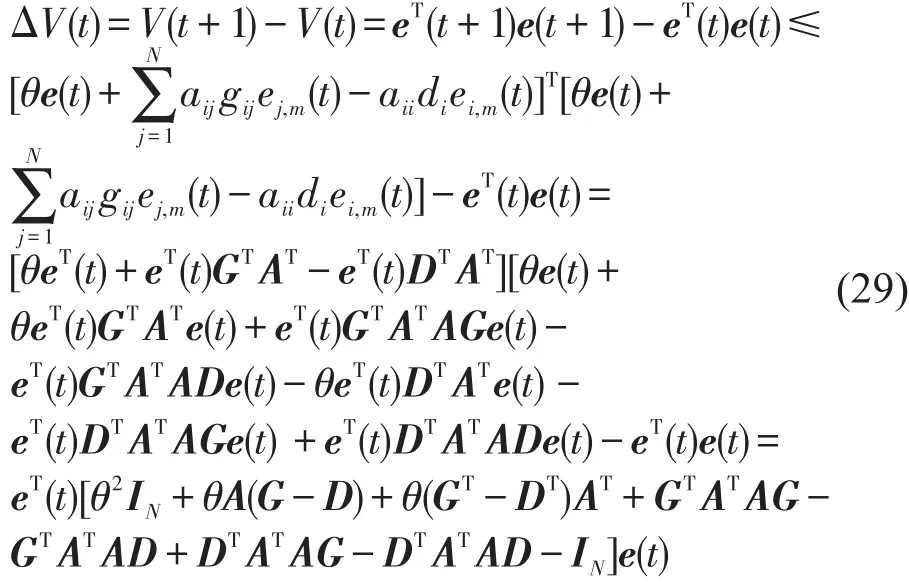
这样，由引理1可以得到式(26)，定理得证.

显然当寻找到合适的θ值后，在G和A已知情况下，通过计算可得到合适的反馈增益矩阵D.其中本文选择拥堵区段上游若干节点为牵制节点，选择控制节点数从1开始不断增加，针对每一种控制节点数采用Matlab中相关工具箱计算，若能得到可行解，这些控制节点数即为牵制节点数，对应得到反馈增益矩阵.若直到选择的节点数为N才能得到可行解，该控制方式为全局同步.

3 仿真实验

3.1 实验对象

采用第1节所述的CTM和节点耦合模型来描述天津市快速路西北小环顺时针方向的交通流过程，该段由南仓道、铁东北路、铁东路、志成路、西青道、西横堤、千里堤组成，17个入口匝道、19个出口匝道和7座立交桥，单向4车道，全长21.8 km；所建模型节点19个，从南仓桥开始按顺时针方向编号，各节点中主线元胞长度(单位：km)：1.08、1.24、0.78、1.05、1.75、1.07、1.27、0.81、1.53、1.34、1.19、1.14、1.10、1.12、1.18、1.08、0.74、1.63、0.67.依据调查和本模型仿真所得数据进行对比，对模型进行校验和参数修正(略)，主要参数：Q为 1 650 veh/(h·lane)，vf为60 km/h，ω为20 km/h，ρd为 45 veh/(km·lane)，kJ为110 veh/(km·lane)；α取0.4，β取0.3；高峰大车占12%.

仿真实验取早高峰7:00-8:00，步长10 s，360个周期.采用4种控制方式进行对比：无任何控制信号施加(No-control Signal,NCS)，本牵制控制方式(Pinning Control Signal,PCS)，全局控制(Global Control Signal，GCS)，CORDIN协调控制算法(CORDIN)，其中GCS采用第2节同样方式推导得到反馈增益矩阵.所有控制方式均采用类似2.1节的协调控制原理作为控制信号施加条件.为进行比较，匝道排队长度在本研究中设置为无限制.

3.2 单次施加控制信号的效果分析

以1个施加协调控制信号过程为例，第9步时节点16密度大于期望值，取θ=0.94，采用第2节方法确定出牵制节点：16、15、14，反馈增益矩阵为diag(0,0,0,0,0,0,0,0,0,0,0,0,0,11.68,12.28,11.33,0,0,0)，图3和4分别为采用本PCS方法与其他3种方法密度误差比较图和节点16道路截面流量比较图.其中GCS的反馈增益矩阵diag(9.54,11.10,6.61,9.24,16.07,9.44,11.39,6.90,13.93,12.07,10.61,10.12,9.73,9.93,10.51,9.54,6.22,14.90,5.54).CORDIN中节点16、15、14、13施加控制信号，节点16采取ALINEA算法，15入口的调节率g2=α1g1，14，13 入口调节率g3=α2g1，α1=0.6，α2=0.3.可以看出：

(1)不控制状态下，节点16密度快速增加，大于临界值，由于系统相态的变化使得节点16流量急剧下降，系统处于拥堵状态，由于城市快速路的封闭性，道路通行效率下降.

(2)使用PCS，通过部分节点的牵制控制，50 s后节点16的密度基本趋于期望值，拥堵抑制，流量也趋于较高水平，通行效率提高，从而初步验证了采用复杂网络同步的思想方法进行城市快速路协调控制的有效性.同时，虽然节点16流量能保持较高水平，但不完全是同一值，密度误差不完全等于0，这是由于城市快速路特点所决定：节点出口匝道流量的各仿真步的不相等所造成的，使得节点密度和流量分别趋于同一值而不完全相等.

(3)使用GCS、CORDIN也能实现密度趋于期望值从而抑制拥堵提高道路通行效率的目的，进一步验证了这些方法的有效性.但GCS和CORDIN分别在第18步(90 s)和第19步(100 s)才能使密度趋于期望值，效率均低于本文方法.这是因为：全局控制范围较大，针对本案例的单拥堵点控制速度较慢不能实现快速的目的，反馈增益矩阵也体现这一点；CRODIN有波动，其参数在控制时起到的比重较大，控制时流量变化较大，使得密度波动较大.

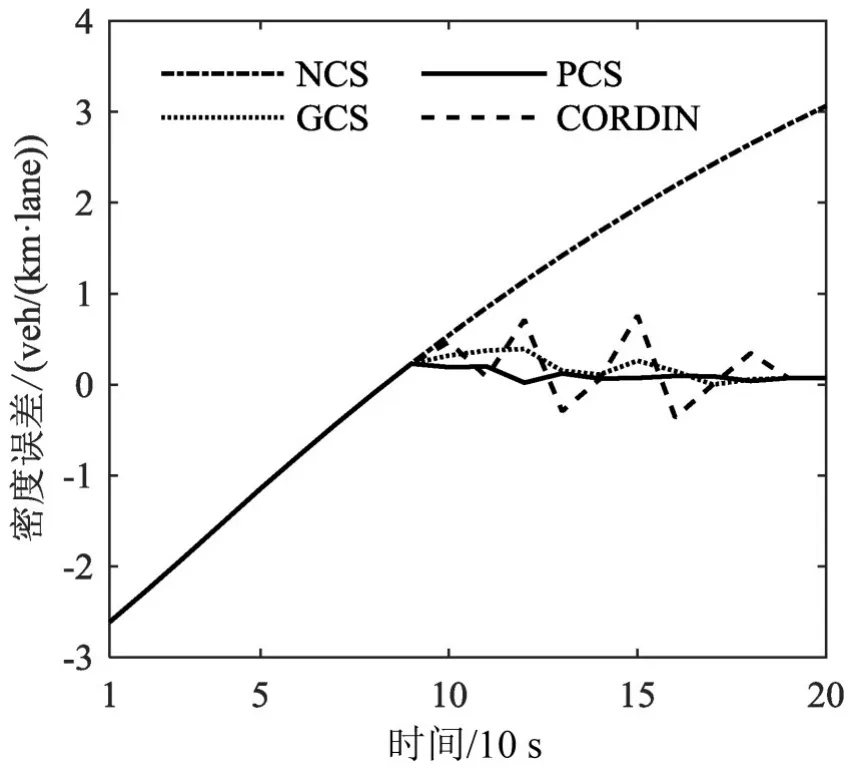
图3 节点16密度误差Fig.3 Density error of node 16

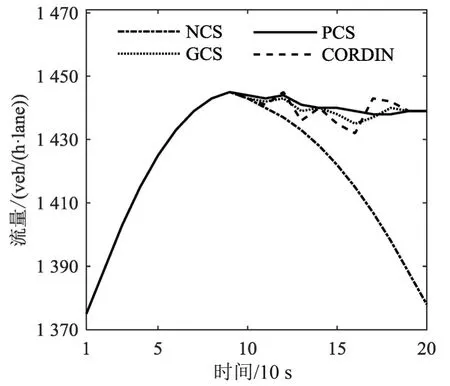
图4 节点16流量变化Fig.4 Flux variation of node 16

3.3 早高峰时间段控制效果比较分析

图5～图8为早高峰7:00-8:00在4种控制方式下各节点密度演化和匝道排队长度变化图，表1为具体流量(1 h内从所有出口匝道、立交桥、节点19流出的车辆数合计)和总旅行时间(所有车辆在实验路网上的行驶时间之和)比较.可以看出：

(1)不控制下节点16密度增加拥堵呈现，并迅速向上游节点15、14、13等蔓延，接近65 veh/(km·lane)左右，呈现拥堵状态，对应的匝道排队长度也迅速增加.而PCS不仅使节点16密度趋近期望值，拥堵抑制，也使拥堵蔓延得到减轻.流量从29 523 veh提高到30 891 veh，总旅行时间从1 051 880 s减少到935 170 s，通行效率得以提高.虽然节点16等匝道排队长度增加较多，但排队长度较长的匝道数较少，整体通行效率得到提高，控制效果优于不控制.从而进一步验证了采用复杂网络同步进行城市快速路协调控制的有效性.

(2)使用PCS方法，每个节点密度整个时间段不完全相等，这是因为即使早高峰也不是都一直加入协调控制信号的，即使在控制信号施加时，可能会出现“部分节点的需求低于需加入主线情况”“出口匝道流出车辆不同”造成的计算偏差.同时，各节点密度整个时间段不相等，这是因为交通的独特特性决定的.一部分节点不需要施加控制信号且密度较低、交通需求较小；控制信号施加的部分节点，出现部分时段交通需求低于计算出需要加入主线的结果，这时虽然不能达到物理意义上真正同步的目的，但随着各个节点密度的降低，控制信号的取消，一样会出现抑制拥堵、提高道路运行效率的目的.

(3)使用GCS和CORDIN方法也能达到抑制拥堵提高通行效率的目的.这两种方法的流量均大于NCS低于PCS，总旅行时间均低于NCS高于PCS.这是因为GCS对全部入口匝道进行控制，造成大部分路段密度波动较大，如图7所示，不需要施加控制信号的匝道人为增加了较长排队长度，如图7所示，不仅带来了社会不公平且造成出行成本的增加，使得通过自组织就能达到的目标，需要额外的人为进行它组织，带来控制成本的增加和社会效益的下降；CORDIN算法建立在经验基础上可实现初步优化，本文PCS方法是通过实时数据计算得到的，具有更佳的控制效果.

图5 NCS下系统密度演化和入口匝道排队长度变化图Fig.5 Evolution diagram of system density and variation diagram of on-ramp using NCS

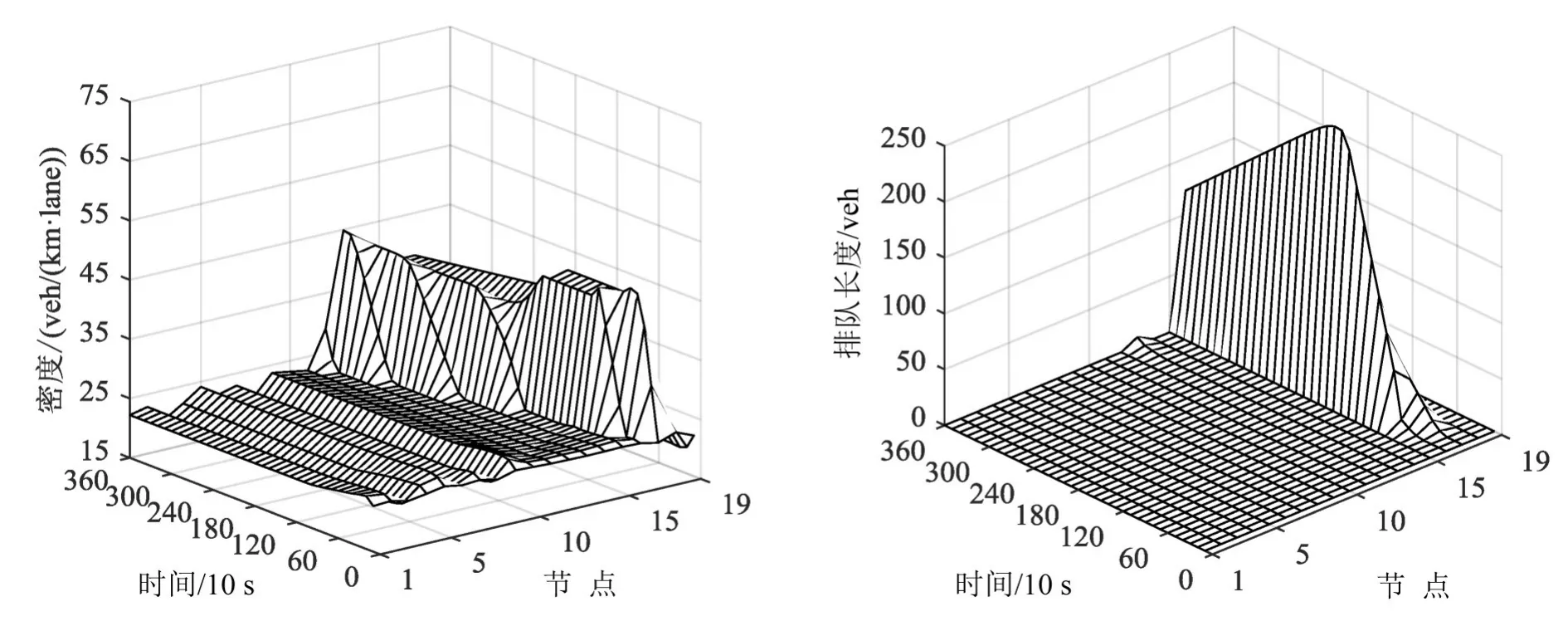
图6 PCS下系统密度演化和入口匝道排队长度变化图Fig.6 Evolution diagram of system density and variation diagram of on-ramp using PCS

图7 GCS下系统密度演化和入口匝道排队长度变化图Fig.7 Evolution diagram of system density and variation diagram of on-ramp using GCS

图8 CORDIN下系统密度演化和入口匝道排队长度变化图Fig.8 Evolution diagram of system density and variation diagram of on-ramp using CORDIN

表1 4种控制方式总旅行时间和流量对比Table 1 Comparison of Total Travel Time(TTT)andflux among four control modes.

4 结论

采用CTM和复杂网络同步理论，建立城市快速路节点耦合模型，以同步为目标尝试设计多入口匝道协调控制器，得到系统同步稳定性条件，通过具体例子予以验证.本研究仅是初步研究，尚需在模型建立、控制器设计等理论上进一步完善，在具体工程应用上对多拥堵点、不同需求下进行仿真实验分析，在此基础上扩展到包括出口匝道、城市一般道路上，为具体工程应用提供条件.

[1]BHOURI N,HAJ-SALEM H,KAUPPILA J,et al.Isolated versus coordinated ramp metering：Field evaluation results of travel time reliability and traffic impact[J].Transportation Research Part C,2013,28(3)：155-167.

[2]CARLSON R C,PAPAMICHAIL I,PAPAGEORGIOU M,et al.Optimal motorway traffic flow control involving variable speed limits and ramp metering[J].Transportation Science,2010,44(2)：238-253.

[3]SHI L,ZHU H,ZHONG S,et al.Synchronization for time-varying complex networks based on control[J].Journal of Computational and Applied Mathematics,2016,301(8)：178-187.

[4]XU M,WANG J L,HUANG Y L,et al.Pinning synchronization of complex dynamical networks with and without time-varying delay[J].Neurocomputing,2017,266(11)：263-273.

[5]GENG N,ZHAO X,XIE D,et al.Congestion mechanism and demand adjustment strategies for double-cell system with bottlenecks[J].Transportation Research Part C,2015,57(8)：122-145.

[6]XIANG J,CHEN G.On the V-stability of complex dynamical networks[J].Automatica,2007,43(6)：1049-1057.

[7]BOYD S,EI GHAOUI L,FERON E,et al.Linear matrix inequalities in system and control theory[M].Philadelphia：Society forIndustrialand Applied Mathematics,1994.