考虑多峰的系统最优动态路径流量分配图解方法研究
2018-06-29赵传林焦朋朋
赵传林,焦朋朋
(北京建筑大学 土木与交通工程学院,北京100044)
0 引 言
掌握交通流量时空分布规律是解决交通拥堵问题的关键.相关研究主要分为2类:静态交通分配模型和动态交通分配模型(动态交通分配模型一直是研究的难点).模型的建立一般基于2类原则:用户均衡和系统最优.本文研究并行网络的系统最优动态交通分配问题.
采用图解法研究该类问题的并不多.基于动态最优性条件并借助变分方法,Munoz等[1]采用图解法描绘了系统最优动态交通分配曲线,得到了并行网络路径流量分配系统最优解.最近,Laval等[2]讨论了动态实时收费对路径流量分配的影响,并采用图解法得到了能够实现动态系统最优的动态实时收费水平.这两篇文章均采用了累计到达曲线(是指到达瓶颈前的累计到达曲线,与交通经济学相关研究的含义,即到达目的地的累计到达曲线不同)已知的假设,即出行者出发时间选择是给定的.此外,Laval[3]还采用图解法研究了动态用户均衡(或用户最优)解.通过放松累计到达曲线已知的假设,考虑出发时刻选择行为,Arnott等[4]和Shen等[5]研究了出发时间和路径选择问题.以上研究均采用了瓶颈模型点排队假设,并在并行网络上展开研究.借助于图解法,Zhao等[6]扩展了Munoz等[1]的方法,并提出了一种新的基于day-to-day的激励策略来实现动态系统最优.不同于Zhao等[6]仅考虑单峰的情形,本文考虑多峰值情形.
采用一类扩展的图解方法,本文将研究并行网络动态路径流量分配系统最优问题.首先给出研究问题描述,其次介绍扩展的求解系统最优动态路径流量分配的图解方法,并应用于多峰值情形.
1 问题描述
考虑包含1个起讫点和2条路径的并行网络,如图1所示,连接起点和终点有2条路径,路径1(高速公路)和路径2(城市街道).令A(t)表示累计到达函数曲线,本文假设该曲线A(t)是给定的,Ai(t)表示路径i的累计到达函数曲线(i=1,2);表示到达率,λ1(t)+λ2(t)=1.假设瓶颈靠近起点处,路径i的瓶颈处容量和自由流时间分别为μi和τi,明显地,τ1<τ2成立.假设函数曲线A(t)已知,即假设每位用户到达瓶颈前的时间是给定的.本文将研究存在多个早高峰的情形,不失一般性,本文仅考虑含有2个峰值的累积到达函数曲线,即到达率先增加再减小,然后再增加最后减小,如图2所示.

图1 并行网络网络结构示意图Fig.1 Parallel network with one OD pair and two routes
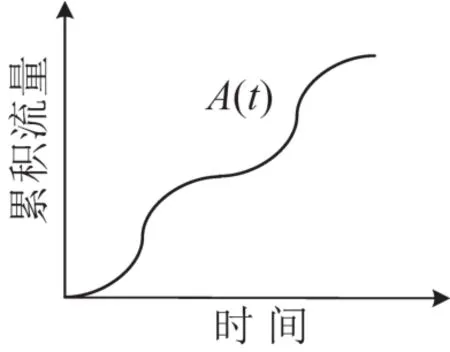
图2 含2个峰值的累计到达曲线示意图Fig.2 Cumulative arrival curve with two-peak demand
假设瓶颈处点排队,令τi(t)表示t时刻到达瓶颈的用户到达目的地的出行时间,包括两部分:自由流时间τi和排队时间wi(t),即

wi(t)可以表示为
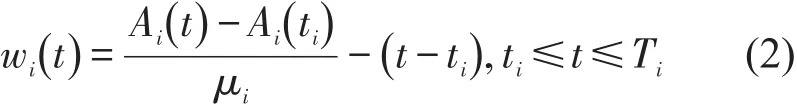
式中:ti和Ti分别表示路径i排队开始和结束的时刻.
2 一类扩展的图解方法
式中:ti和Ti分别表示路径i排队开始和结束的时刻.
本文通过图解法来得到系统最优时的每条路径的流量分配值,即研究A(t)如何在并行路径上实
2.1 Munoz和Laval(2006)图解方法介绍
Ziliaskopoulos[7]介绍了动态情形系统最优性条件,即对于所有的出发时刻,具有最小边际出行成本的路径会被用户选择.某条路径的边际出行成本包括2部分:一是,该路径上增加1位用户给整个系统带来总延误的增加;二是,该用户选择该路径的出行时间.考虑点排队模型,如果某条路径已经处于排队状态,此时若该路径增加1位用户会影响后续所有的出行用户,直至排队结束.
基于最优性条件,Munoz等[1]借助变分法采用图解法首次得到了动态路径流量分配系统最优解.以图1所示2条路径为例,令T1为路径1上排队消失的时间,T2为被分配在路径2上的最后一个用户的出发时间.假设用户总数N固定,在系统最优时,一条路径上(比如路径1)人数增加dN所导致的系统总排队时间的增加(即路径1总排队时间的增加,dN(T1-T2))等于另一条路径上(即路径2)人数减少dN所导致的总自由流出行时间的减少(即,dN(τ2-τ1)).两式相等,我们得到系统最优性条件的数学表达式为

式(3)的具体细节,可参阅文献[1].
为了实现系统最优性条件,Munoz等[1]介绍了一类图解方法,当路径2瓶颈处容量无穷大时,即μ1=c1,μ2=∞,c1表示路径1瓶颈处的容量为常数,沿垂直方向自上向下移动累计到达曲线,直至满足系统最优性条件式(3),具体图解法过程如图3(a)所示;当路径2瓶颈处容量为某一常数时,即μ1=c1,μ2=c2,水平延长A(t),如图4(a)中水平虚线.在水平虚线上选择点M为起点,向左画出斜率为μ1的线段,保证水平投影长度为τ2-τ1;然后,画出斜率为μ1+μ2的直线.记两段线段为累计离开曲线,自右向左移动该线,直至再次与A(t)相切,切点对应的时刻为t2,具体图解法过程如图4(a)所示.根据图3(a)和图4(a),可以直接得到2条路径流量分配系统最优解,如图3(b)~(c)和图 4(b)~(c).以图 3为例,系统最优解如表1所示.

图3 图解法示意图(μ1=c1,μ2=∞)Fig.3 Graphical solution method(μ1=c1,μ2=∞)
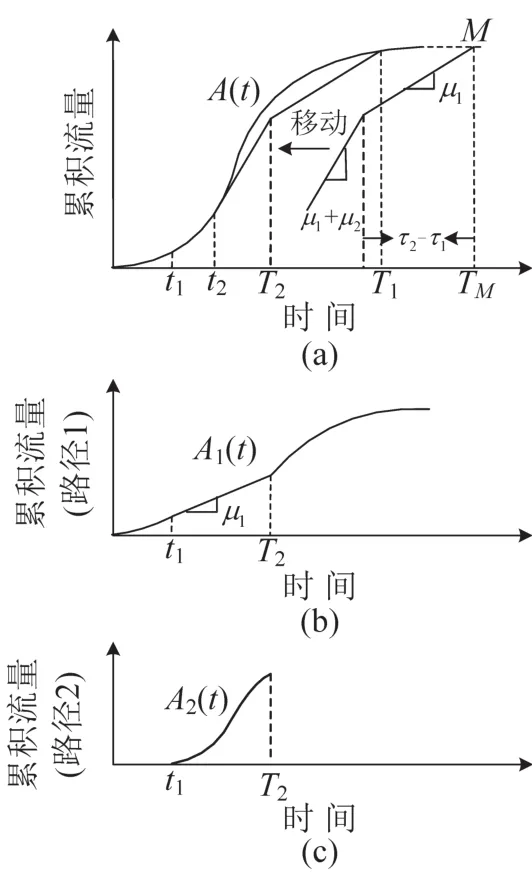
图4 图解法示意图(μ1=c1,μ2=c2)Fig.4 Graphical solution method(μ1=c1,μ2=c2)

表1 系统最优流量分配结果(μ1=c1,μ2=∞)Table 1 Optimal solution(μ1=c1,μ2=∞)
2.2 扩展的图解方法
不同于Munoz等[1]的图解方法,本文介绍一类扩展的图解方法,并应用于多峰情形:自下向上移动累计离开率曲线,直至满足最优性条件式(3).仍以图1所示的2条路为例,研究2种情形,一种是μ1=c1,μ2=∞;另一种情形是μ1=c1,μ2=c2.
情形 1μ1=c1,μ2=∞.
图5给出了具体的图解法过程,t1时刻流量到达率为λ(t1)=μ1.具体的图解法过程可描述为:
Step 1沿水平方向延长累计到达曲线A(t),如图5中水平虚线.在时刻t1,画斜率为μ1的直线L(t),即累计离开率曲线.
Step 2以K1点(t1,A(t1))为起点,沿垂直方向自下向上移动L(t)至与A(t)相交于3点,即K2点(t2,A(t2)),K3点(t3,A(t3))和K4点(t4,A(t4)).
Step 3比较t3-t2和t4-t3与τ2-τ1的关系.存在4种情况:第1种情况,t3-t2≤τ2-τ1和t4-t3≤τ2-τ1,在这种情况下,通过计算变分,增加或减少路径1的流量均会增加系统总时间,3个交点K2,K3和K4决定了系统最优时的流量分配结果,具体结果如表2所示;第2种情况,t3-t2>τ2-τ1和t4-t3<τ2-τ1,这种情况下,只需要继续向上移动线段K2K3直至t3-t2=τ2-τ1成立,2个新交点与点K3和点K4共同决定了系统最优时的流量分配结果;第 3 种情况与第 2 种类似,即t3-t2<τ2-τ1和t4-t3>τ2-τ1成立;第 4 种情况,t3-t2>τ2-τ1和t4-t3>τ0-τ1,此时线段K2K3和K3K4均需要继续垂直向上移动直至t3-t2=τ0-τ1和t4-t3=τ2-τ1成立,得到的4个新交点决定了系统最优时的流量分配结果.
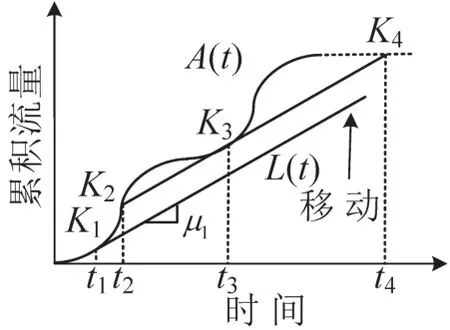
图5 含双峰的图解法示意图(μ1=c1,μ2=∞)Fig.5 Graphical solution method with two-peak demand(μ1=c1,μ2=∞)

表2 一种可能的含双峰的系统最优流量分配结果(μ1=c1,μ2=∞)Table 2 One possible optimal solution withtwo-peak demand(μ1=c1,μ2=∞)
情形 2μ1=c1,μ2=c2.
图6给出了具体的图解法过程,λ(t1)=μ1,λ(t2)=μ1+μ2,记点(t2,A(t2))为K1点.具体图解法过程描述如下:
Step 1 类似于情形1,沿水平方向延长累计到达曲线A(t),如图6水平虚线.以K1点为起点,画斜率为μ1和μ1+μ2的直线,分别为K1K2和K1K3.为了保证最优性条件式(3),线段K1K2的水平投影长度为τ2-τ1.与单峰情形不同,直线K1K3与A(t)的位置关系存在两种情况,分别如图6(a)和图6(b)所示,下面分别分析这两种情况.
Step 2图6(a)和图6(b)分别讨论.
图6(a)中,沿着K1K3向上移动K1K2,直至再次与A(t)相交,记为点K4.点K1,K3和K4决定了流量分配系统最优解.基于图6(a),详细的流量分配结果如表3所示.需要指出的是时间区间(t2,T2) ,p∈(0 ,λ(t)-μ1-μ2)和q∈(0 ,λ(t)-μ1-μ2),而且p和q同时满足约束条件p+q=λ(t)-μ1-μ2.这说明该区间流量分配结果不唯一,Munoz等[1]也分析了流量分配系统最优解的不唯一性.

图6 含双峰的图解法示意图(μ1=c1,μ2=c2)Fig.6 Graphical solution method with two-peak demand(μ1=c1,μ2=c2)

表3 含双峰的系统最优流量分配结果1(μ1=c1,μ2=c2)Table 3 The first possible optimal solution with two-peak demand(μ1=c1,μ2=c2)
图 6(b)中,直线K1K3与A(t)相交于第1个峰值段,以K1点为起点,沿K1K3向上移动K1K2,直至端点K2与A(t)相交或者K1K2与A(t)相切,切点记为K5,左侧端点记为K4.第2个峰值段的分析与第1个峰值段类似,可以找到 3个点K6,K7和K8,其中在K6点,λ(t6)=μ1+μ2.6个点Kj,j=1,4,5,…,8,决定了流量分配系统最优解,具体结果如表4所示.
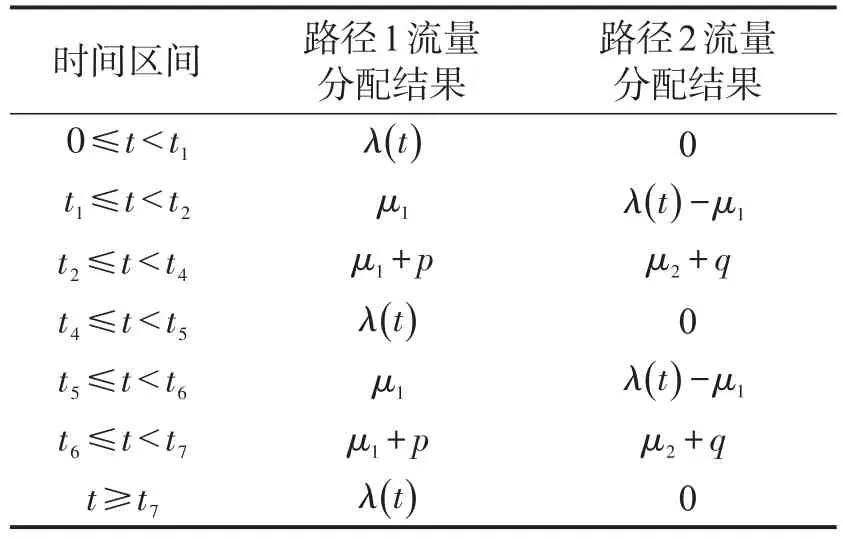
表4 含双峰的系统最优流量分配结果2(μ1=c1,μ2=c2)Table 4 The second possible optimal solution with two-peak demand(μ1=c1,μ2=c2)
3 算 例
本节给出2个算例来说明本文两种情形的分析结果.
算例1参数设定为μ1=0.5,μ2=∞,累计到达曲线A(t)为分段连续可微函数,如式(4)所示.
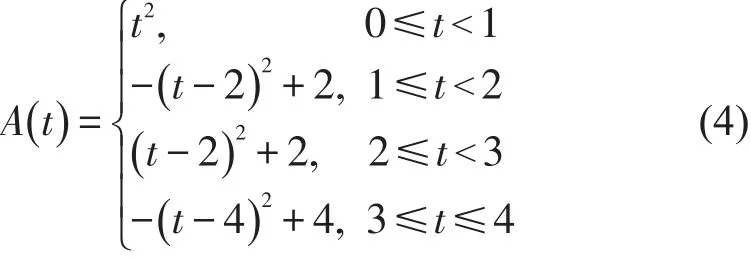
从式(4)可知,曲线的斜率先增后减,然后再增加,再减小.结合图5的图解法求解过程,图7给出了图解法的求解结果.由于A(t)上横坐标为t1点和t3点的斜率为μ1=0.5,可以很容易地求得:t1=0.25,t3=2.25,进而可求得:t2=1.75+ 1 8,t4=6.125.根据A(t)的函数表达式和μ1=0.5,可以发现t4-t3≥t3-t2.按照情形1中Step3的分析,比较t3-t2=0.5- 1 8 和t4-t3=3.875分别与τ2-τ1的关系.如果τ2-τ1≥3.875成立,则路径1和路径2的流量分配结果如表5所示;如果0.5-1 8≤τ2-τ1≤3.875成立,则需要继续垂直向上移动图5中的线段K3K4,直至t4-t3=τ2-τ1成立;如果τ2-τ1≤0.5- 1 8成立,则需要继续垂直向上移动图 5 中的线段K2K3和K3K4,直至t3-t2=τ2-τ1和t4-t3=τ2-τ1成立.
算例2考虑图6(a)情形,参数设定为μ1=0.3,μ2=0.2,τ2-τ1分别取1.0和1.5;A(t)仍然为式(4)所示.当τ2-τ1=1.0时,按照图6(a)的图解法过程,计算可以得到:t1=0.15,t2=0.25,tk=1.25,T2=7.525,T1=8.525.斜率为0.5的直线横坐标为T2点对应的纵坐标为3.7;求解A(t)=3.7得到tj=3.45.当τ2-τ1=1.5时,可计算得到:t1=0.15,t2=0.25,tk=1.75,T2=7.225,T1=8.225;斜率为0.5的直线横坐标为T2点对应的纵坐标为3.55;求解A(t)=3.55得到tj=3.33.系统最优路径流量分配结果如表6和表7所示,p值的取值范围均为p∈(0 ,λ(t)-0.5),且p+q=λ(t)-0.5.从表6和表7的结果可以发现,τ2-τ1取值的不同仅仅影响到tj的值.
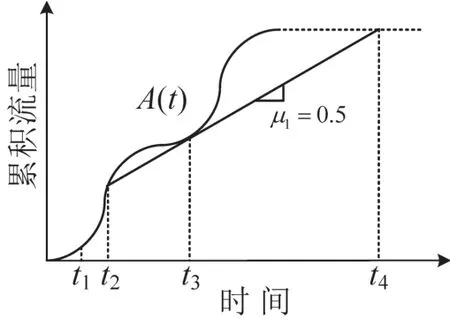
图7 情形1图解法算例(μ1=0.5,μ2=∞)Fig.7 Graphical solution method for case 1(μ1=0.5,μ2=∞)

表6 情形2系统最优路径流量分配结果(μ1=0.3,μ2=0.2,τ2-τ1=1.0)Table 6 Optimal solution for case 2(μ1=0.3,μ2=0.2,τ2-τ1=1.0)

表7 情形2系统最优路径流量分配结果(μ1=0.3,μ2=0.2,τ2-τ1=1.5)Table 7 Optimal solution for case 2(μ1=0.3,μ2=0.2,τ2-τ1=1.5)
4 结论
Zhao等[6]研究了一类扩展的图解法求解动态路径流量分配系统最优解,但仅仅考虑单峰的情形,本文扩展至多峰情形.基于瓶颈模型点排队假设、系统最优性条件和图解方法的具体实施过程,扩展的图解方法可以应用于含有1个OD的一般并行网络[6],不适用于一般结构网络.
本文考虑了两种情形,即高速公路瓶颈容量为常数,城市街道瓶颈容量分别为无穷大和常数,给出了每种情形下的路径流量分配结果.但是结果的获得是基于瓶颈处点排队和累计到达曲线已知的假设,在后续的研究中,将综合考虑出发时间和路径选择问题,进一步分析流量分配结果.此外,放松点排队和固定需求假设,结合宏观基本图的流量—速度—密度关系,采用图解法研究动态流量分配结果也是即将开始的工作.
[1]MUNOZ J C,LAVAL J A.System optimum dynamic traffic assignment graphical solution method for a congested freeway and one destination[J].Transportation Research Part B:Methodological,2006,40(1):1-15.
[2]LAVAL J A,CHO H W,MUNOZ J C,et al.Real-time congestion pricing strategies for tollfacilities[J].Transportation Research Part B:Methodological,2015(71):19-31.
[3]LAVAL JA.Graphicalsolution and continuum approximation for the single destination dynamic user equilibrium problem[J].Transportation Research Part B:Methodological,2009,43(1):108-118.
[4]ARNOTT R,DE PALMA A,LINDSEY R.Departure time and route choice for the morning commute[J].Transportation Research Part B:Methodological,1990,24(3):209-228.
[5]SHEN W,ZHANG H M.On the morning commute problem in a corridor network with multiple bottlenecks:Its system-optimal traffic flow patterns and the realizing tolling scheme[J].Transportation Research Part B:Methodological,2009,43(3):267-284.
[6]ZHAO C L,LECLERCQ L.Graphical solution for system optimum dynamic traffic assignmentwith day-to-day incentive routing strategies[C].The 9th International Workshop on Computational Transportation Science,Lanzhou Jiaotong University,Lanzhou,2017.
[7]ZILIASKOPOULOS A K.A linear programming model for the single destination system optimum dynamic traffic assignment problem[J].Transportation Science,2000,34(1):1-12.
