基于自回归条件持续期模型的疲劳驾驶研究

毛树华，王先朋，文江辉,，吴超仲，肖新平

(武汉理工大学a.理学院；b.智能交通系统研究中心，武汉430070)

0 引 言

道路交通安全，一直以来都是人们关注的热点问题，而疲劳驾驶是严重交通事故的主要原因之一.统计显示，20%左右的全部交通事故，以及40%以上的重大交通事故是疲劳驾驶造成的[1]，因此，疲劳驾驶的检测具有重要意义.其代表性的研究主要从驾驶员的生理参数、面部表情，驾驶行为3个方面进行，前两个方面在应用中需要采用接触式检测装置及图像处理的手段，成本较高且不适于实际应用；第3种方法是根据车辆自身数据(车辆的速度、侧向加速度等)进行检测，成本低，同时采用非接触式检测方式，实用性强[2].因此，本文从时间间隔的视角根据车辆自身的数据(车速)进行疲劳驾驶方面的研究，提出车速变化持续期的概念来刻画车速变化状态，根据时间间隔序列(车速变化持续期)的迅速变异性，将自回归条件持续期模型引入交通领域，来拟合车速变化持续期序列的波动特性，从侧面了解驾驶员的驾驶状况，从而为进一步研究时间间隔视角下疲劳驾驶行为检测打下基础.

1 自回归条件持续期模型

考虑时间序列{t0,t1,…,tn,…} ，t0＜t1＜…＜tn＜…，我们定义车速变化持续期为xi=ti-ti-1，这是两个事件发生(车速变化达到某一程度则认为事件发生)之间的时间间隔，ti是第i个事件发生的时间.可以将这个时间过程，视为一个简单的点过程，与每个事件发生时间对应的有一个计数函数N(t),t≥0，为到第i个事件发生时刻为止所发生的事件次数.ψi=E(xi|Fi-1)表示第i-1和第i次事件发生的持续期基于信息集Fi-1(即{xi-1,xi-2,…,x1})的期望，满足

假设

式中：εi为独立同分布的非负随机变量，εi～i.i.d，并且E(εi)=1，其密度函数是 p(ε|φ)；αm(m=1,2,…p)，βn(n=1,2,…,q)，ω均为待估计的参数.经典ACD模型中，εi遵从标准的指数分布和Weibull分布，分别称为EACD(p,q)模型、WACD(p,q)模型[3].

相对EACD模型而言，WACD模型更加灵活.WACD模型中数据分布函数的形状参数γ小于1时，模型表现为递减机会函数，即出现长持续期的可能性递减；若γ＞1，则模型表现为递增机会函数，即出现长持续期的可能性递增.

由于自回归条件持续期模型的建立是基于对随机误差项分布假设之上的，本文的参数估计采取的是准极大似然估计法，其似然函数如式(5)所示.

假设εi～Weibull(1,γ)，不失一般性，取 p=1，q=1，则xi的分布函数为

x1,x2,…,xN的联合分布函数为

γ,α,β,ω的似然函数为

参数估计值根据式(5)，采用Nelder-Mead单纯形法得到.

2 数据预处理与车速变化持续期的统计特性

数据来自某研究所做的实验数据，实验地点是位于武汉市西北部的汉十高速.实验数据采集时长大约为30 000 s，即8 h左右，车速采集的频率为77 Hz，数据约有200万条.首先处理原始数据得到车辆正常行驶的车速数据.文献[5]的研究表明疲劳驾驶时，车速标准差随疲劳程度上升有显著差异，故选取时间区间内车速变化的标准差达到某一阈值认为事件发生.对于时间区间，本文主要考虑两个方面，一是在一个时间区间内驾驶员精神状态的变化程度不大，这样才能表示持续期的意义；二是这个时间区间内速度需要有较大的变化以增加其辨识度.此外，获得数据的频率不同也会影响区间时间的选定.一般来说，区间时间最好在60 s以内.基于实验得到的数据频率，为了研究的方便，在本文中时间区间定为5 s.以5 s为间隔计算车速的标准差，再取适当的阈值作为事件发生的标志，当车速的标准差达到阈值或者以上时，我们认为一次事件发生，此时提取这个事件的起始时间与终点时间的差，作为一个车速变化持续期.针对阈值的选取，本文参考文献[6]中交易量持续期所定阈值方法，选取车速标准差的均值的一定倍数作为阈值，考虑到单位时间内车速变化(标准差)存在着上限和下限且不同驾驶员的阈值也存在着不同，以各驾驶员车速标准差的1倍均值作为本文的阈值.

按照上述的处理方法，经过处理得到持续期间的描述性统计结果，共35个样本，其描述统计如表1所示.

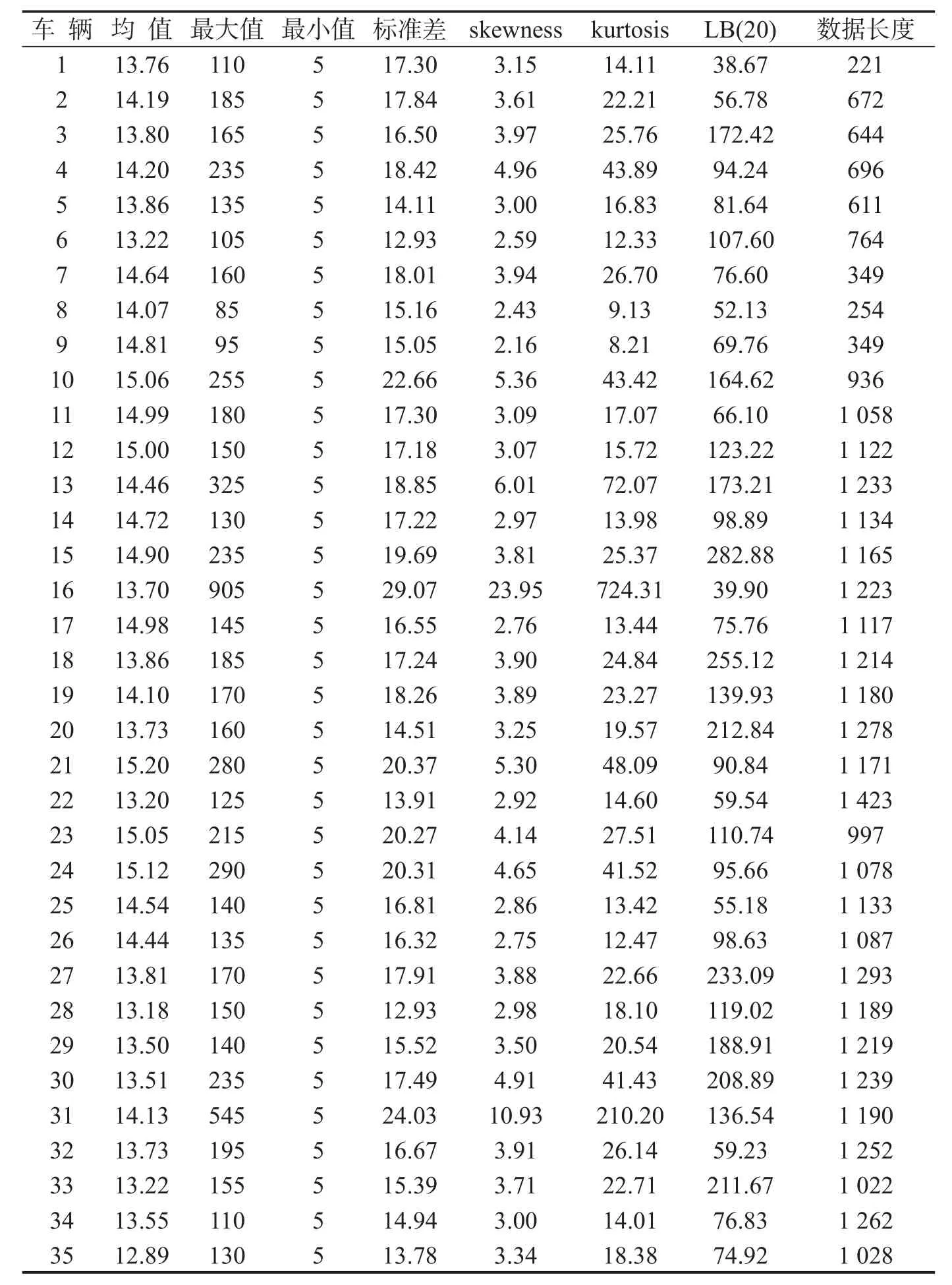
表1 持续期间的描述性统计Table 1 Descriptive statistics for duration

从表1可以发现，虽然各个驾驶员的续期序列存在着差异，但所有续期的峰度值都是远大于3的，说明其不服从正态分布.图1给出了样本的车速变化持续期序列图(限于篇幅图中只给了12、13、14号车的序列值)，在图1的序列图中还可以注意到，续期在一些区间时而稳定时而波动较大，存在一定程度的波动集群特征.时间序列的波动性意味着时间序列的条件方差随着时间的变动而变动，且可能依赖于先前已出现的序列值.因此，需要 对时差序列的相关性做进一步分析.

图1 12、13、14号车车速变化持续期Fig.1 12,13,14 car speed variation duration sequence diagram

对于序列自相关的检验，一般采用的方法有计算ACF和PACF并观察其图像及Ljung-Box检验等.以12、13、14号车为例，图2和图3分别显示了3个样本的自相关(ACF)和偏自相关(PACF).从图中可以发现，续期存在着明显的序列自相关，表1中35辆车的Ljung-box统计量均远远超过显著性水平为5%时的临界值31.41，可以拒绝所有自相关系数为零的假设，表明样本的车速变化续期均存在较强的持续性和聚类性.这为本文使用ACD模型来分析车速变化持续期序列提供了有力的证据.

图 2 12、13、14号车的ACF相关图Fig.2 Autocorrelation function of car 12,13,14

图 3 12、13、14号车的PACF相关图Fig.3 Partial autocorrelation function of car 12,13,14

3 实证研究

一般而言，模型的阶数过高从而导致模型复杂度过高，会影响模型的拟合效果，因此本文研究经典ACD(1,1)模型以探讨该模型在交通领域的适应性.处理过后得到车速变化持续期序列数据，可以使用这些期间数据来估计WACD(1,1)模型和EACD(1,1)模型参数.

式中：xi为处理后得到的车速变化持续期.

对整体车速变化持续期进行估计，估计的方法采用的是准极大似然法.在参数估计的过程中，数值算法采用了Nelder和Mead提出的Neldermead单纯形算法.

表2和表3给出了35辆车的车速变化持续期的EACD(1,1)模型和WACD(1,1)模型参数估计结果.

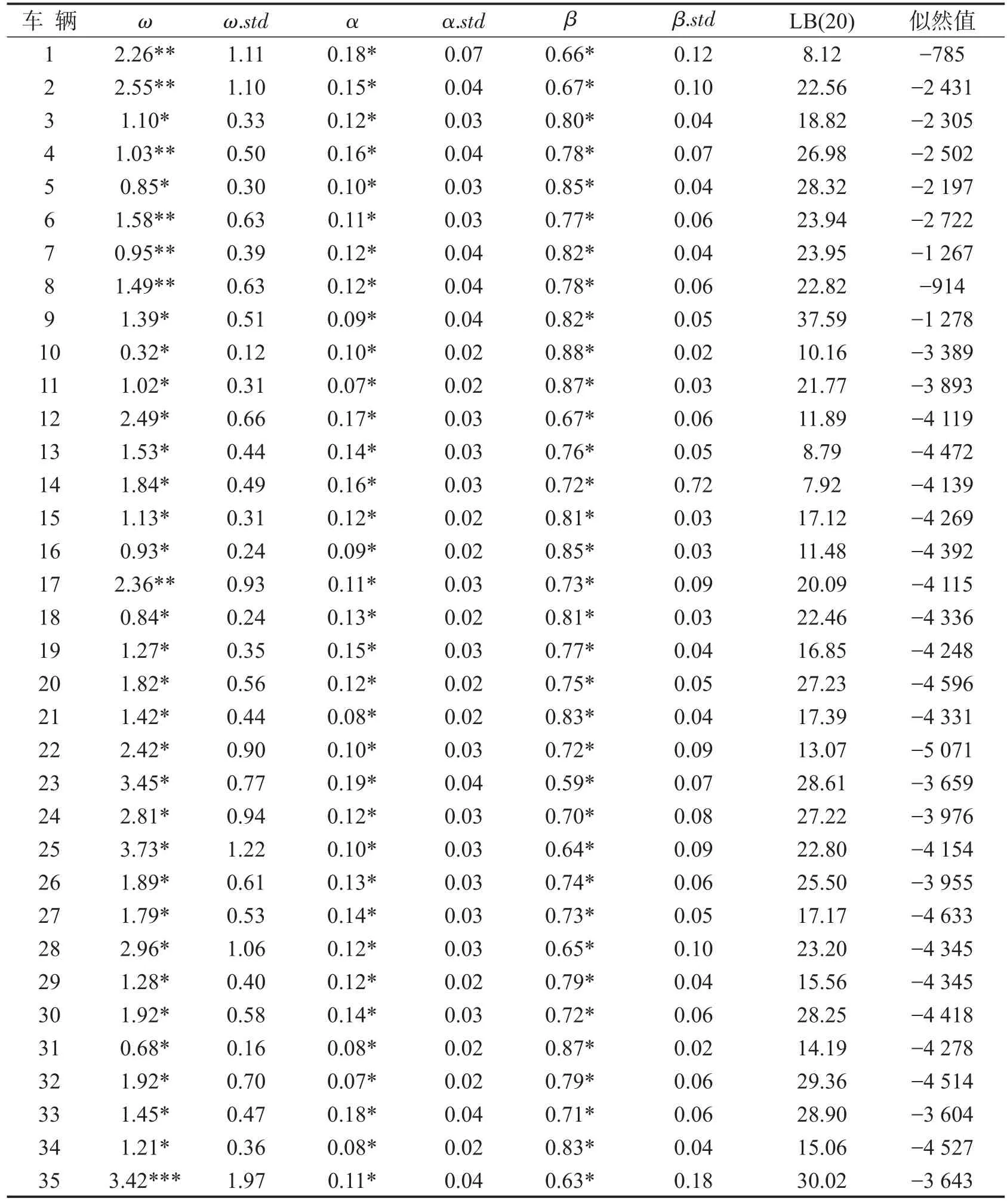
表2 EACD模型参数估计Table 2 Parameter estimation of EACD model

表3 WACD模型参数估计Table 3 Parameter estimation of WACD model

为了检验ACD模型是否能够很好地模拟到车速变化持续期动态性和分布特征及可靠性，需要对模型的残差进行诊断检验.定义残差形式为

因为残差是模型不能预测的部分，所以如果这些残差是i.i.d，那么就可以认为模型是可靠的.以12、13、14号车为例，图4为3辆车的EACD模型残差的自相关图，图5为3辆车的WACD模型残差的自相关图.同时从表2和表3可以看到35辆车模型估计后的残差Ljung-box统计量都低于显著性水平为5%时的临界值31.41，可以接受残差所有自相关系数为零的假设，两个模型消除了序列自相关.

图 5 12、13、14号车WACD(1,1)模型残差的ACF相关图Fig.5 Autocorrelation function of residual error of car 12,13,14 for WACD(1,1)model

表2和表3的结果表明，35辆车WACD模型和EACD模型的ω、α、β估计值相差不很显著，其原因在于Weibull分布的形状参数γ等于1时为标准指数分布，通过表中可以看出WACD模型的极大似然估计值都大于EACD模型，故而WACD模型比EACD模型的效果要好一点，这与理论相符合.

表3中，ω、α、β、γ除个别外在5%的置信概率内显著不为0，且α+β＞0.8，表明车速变化持续期自身存在强自相关性，表现出聚类现象；3辆车的常量参数ω相差比较大，表现了驾驶员的个人驾驶习惯的差异，即驾驶员在驾驶过程中会做加减速的操作，性格稳重的驾驶员的车速波动相对性格急躁的驾驶员要小一点；α、β参数估计值的差异说明了驾驶员对实际驾驶环境的敏感性不同，实际驾驶环境对驾驶员影响比较小时，前期持续期对后续持续期有更大的影响.35辆车的车速变化持续期WACD(1,1)模型的形状参数γ估计值均大于1.当γ＞1时，模型表现为递增机会函数，即在下一瞬间结束长持续期的可能性变大.可以推断35辆车的车速变化持续期出现长的车速变化持续期的可能性是递增，这说明了驾驶员的驾驶状态整体上有着变差的趋势，即疲劳程度会随着持续驾驶时间的积累逐渐地提高.

在实际驾驶过程中，驾驶员的驾驶状态总是一个动态的过程.当实际期间大于条件预期期间，即车速变化达到一定程度，实际所花费时间大于期望时间，说明驾驶员的疲劳程度逐渐提高，驾驶状态有变差的可能；当实际期间小于条件预期期间，说明驾驶员经过调整，驾驶状态有变好的可能.

综合以上对各驾驶员的统计实证分析结果，可以看出，通过构建车速变化持续期序列波动的ACD模型，为观测不同驾驶员的车辆行为，提供了一个新的微观视角.对于基于时间间隔视角的疲劳驾驶应用研究，可由该分析方法获取关于驾驶行为更多、更准确的内在统计特征，进而为后续的研究工作提供依据.在本文研究的基础上进一步将疲劳程度因子引入模型研究车速变化持续期与疲劳程度的关系，进而可从时间间隔角度出发实现疲劳驾驶识别.

4 结 论

利用EACD模型和WACD模型，从时间间隔的角度对车速变化进行研究，从侧面分析了驾驶员的驾驶状况.本文的实验结果表明，其能够较好地拟合车速变化持续期序列的波动特性，可将ACD模型应用到车速变化中，从而可以有效利用这一信息来判断驾驶状态.进一步将疲劳程度因子引入模型研究车速变化持续期与疲劳程度的关系，进而可从时间间隔角度出发实现疲劳驾驶识别.该模型在其他更多类型道路和驾驶员的车辆行为数据上的普适性和模型参数选取上仍有待进一步研究.

[1]HU S,ZHENG G,PETERS B.Driver fatigue detection from electroencephalogram spectrum after electrooculography artefact removal[J].Iet Intelligent Transport Systems,2013,7(1)：105-113.

[2]袁翔,孙香梅.疲劳驾驶检测方法研究进展[J].汽车工程学报,2012,2(3)：157-164.[YUAN X,SUN X M.Development of driverfatigue detection method research[J]. Chinese Journal of Automotive Engineering,2012,2(3)：157-164.]

[3]ENGLE R F,RUSSELL J R.Autoregressive conditional duration：A new model for irregularly spaced transaction data[J].Econometrica,1998,66(5)：1127-1162.

[4]NELDER J A,MEAD R.A simplex method for function minimization[J].Computer Journal,1965,7(4)：308-313.

[5]毛喆,严新平,吴超仲,等.疲劳驾驶时的车速变化特征[J].北京工业大学学报,2011(8)：1175-1183.[MAO Z,YAN X P,WU C Z,et al.Analysis of velocity changing rules under driving fatigue[J].Journal of Beijing University of Technology,2011(8)：1175-1183.]

[6]祝长江.基于交易量持续期的股市流动性研究[D].上海：上海师范大学,2014.[ZHU C J.Research on the stock market liquidity of the trading volume duration[D].Shanghai：Shanghai Normal University,2014.]