波流作用下围油栏油水界面失稳机理分析

时 洋，李绍武，张华勤，陈汉宝，周 然



波流作用下围油栏油水界面失稳机理分析

时 洋1，李绍武1，张华勤2，陈汉宝2，周 然2

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 交通部天津水运工程科学研究所，天津 300456)

海上溢油对自然资源造成严重的环境损害．围油栏是一种常用收集海上溢油设备．围油栏工作效率因常受到波浪和水流等因素的影响而大大降低，油水界面不稳定是围油栏失效的主要原因．基于特征函数理论，研究了两层流体中表面波模态的波浪与刚性围油栏的相互作用问题．以水流流速、油水密度比值、油层厚度、围油栏吃水深度和波要素等为参数，对波流作用下压力梯度的变化及其对油水界面稳定性的影响进行了系统性分析．研究结果表明：液体压力垂直结构决定了油水界面的稳定性，油水界面处的液体压力梯度才是判断油水界面稳定性的依据．

溢油；围油栏失效；油水界面不稳定性；临界压力梯度；特征函数法

围油栏失效的临界条件是围油栏设计理论的基础性课题．了解一定波流条件下围油栏的失效机理是合理确定围油栏失效临界条件的前提，也是围油栏应用过程中根据具体波、流条件进行参数选择的重要依据．围油栏工作失效主要表现为3种典型情形：第1种情况是围油栏水上高度不足，油面越过围油栏顶部而失效，称为越顶失效；第2种情况是由于油、水界面低于围油栏底端高度，溢油从围油栏底部泄露，称为油层流失失效[1-3]；第3种情况是油、水界面达到临界失稳时，溢油被水流中的小尺度涡撕扯脱落，形成油滴，再经大尺度涡旋的对流扩散作用，溢油越过围油栏，称为夹带失效[4]．本文主要讨论油水界面失稳的第2种情况．

单纯水流条件下，在围油栏底端附近存在一定垂向负压梯度，这种负压梯度是造成围油栏前油水界面不稳定的原因．Kordyban[5]在势流假设下导出一个依赖于负压梯度的油水界面稳定性判断方程．Ertekin等[6]通过数值方法在层流状态下求解方程，得到了围油栏附近液体压力梯度分布，并根据液体压力分布讨论了油水界面的稳定性．他们假设油膜在油水界面稳定性问题中的作用很小，所以没有考虑油膜的存在对整个流场的改变，这种假设与实际情况有较大出入．刘诚等[7]考虑围油栏前流体运动的强紊动特征，建立了油水湍流模型，较全面地研究了围油栏前液体压力梯度及油水界面稳定性随油水密度比值、水流流速、围油栏吃水深度和油的运动黏度变化．波浪条件下，无论是自由油面，还是油水交界面的振荡幅度都将得到强化，围油栏也因此较无波浪情况更易失效，如，Amini等[8]通过实验研究认为波浪可以减小围油栏初始失效流速，并认为波浪参数对围油栏失效的影响主要体现在波陡这一参数上，但Lee等[9]指出波浪作用既可能增大初始失效流速，也可能减少初始失效流速．有关波浪作用对于围油栏失效的影响目前存在截然相反的结论．

本文采用特征函数法[10]，研究油、水分层流体在围油栏栏前的液体压力垂直结构，提出波流共存条件下油、水界面稳定性判断方程．

1 单向流情况下油膜稳定性力学分析

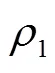
 (1)

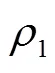
油膜单元受到向上的力为

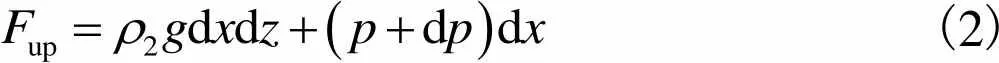
 (2)

由油膜单元垂向平衡条件得

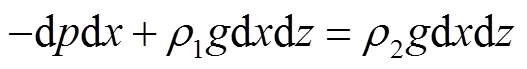
即有

 (3)

另一方面，假设围油栏下游区域不发生水流脱离，围油栏周围流场可近似按势流理论进行求解，问题简化为突出边界的绕流问题．借助施瓦兹-克里斯托弗变换(S-C变换)，将物理域中复平面下的实际流场映射到平面(图2)，其中平面下的、和点分布对应平面的、和点．

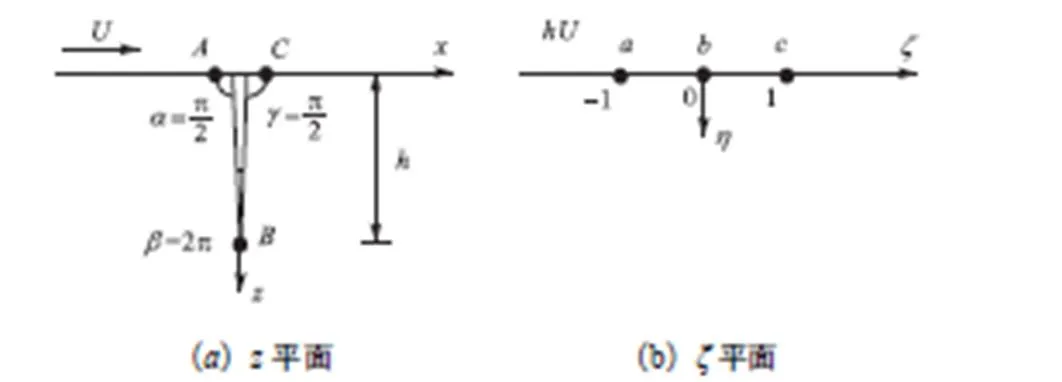
图2 S-C坐标转换图

建立平面与平面间的映射关系

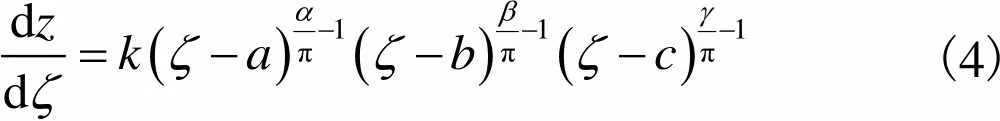
 (4)

式中为系数．将＝π/2，＝2π，＝π/2，＝-1，＝0，＝1代入式(4)得

 (5)

将式(5)积分得

 (6)

式中0为积分常数，可通过、、与、、对应关系求得．

由＝1，＝0，得0＝0；再由＝0，＝i，得＝．于是，得到由平面到平面的S-C映射关系为

 (7)

 (8)

令平面中平板绕流复势为()，平面中均匀流复势为()．注意到，两个平面下复势应该相同，即()＝()，由平面无穷远处复速度表达式d()/d＝以及平面与平面间的映射关系 d/d＝，可知，平面无穷远处复速度表达式为d()/d＝d()/d＝d()/d·d/d＝，平面复势表达式为

 (9)

式中为入口水平流速．

由式(7)和式(9)可得到平面中的复势为

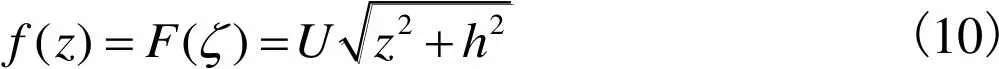
 (10)

平面中的复速度为

 (11)

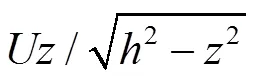
 (12)

进而有

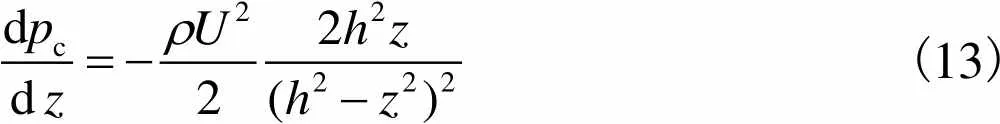
 (13)

2 波流共同作用下油膜稳定性分析

波流作用下围油栏周围波浪场可以采用势流理论求解．根据线性叠加理论，整个流体的速度势可以表达成

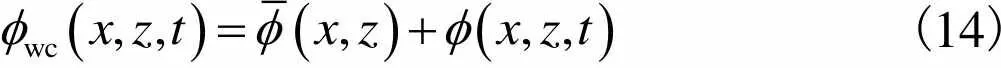
 (14)

2.1 迎浪侧

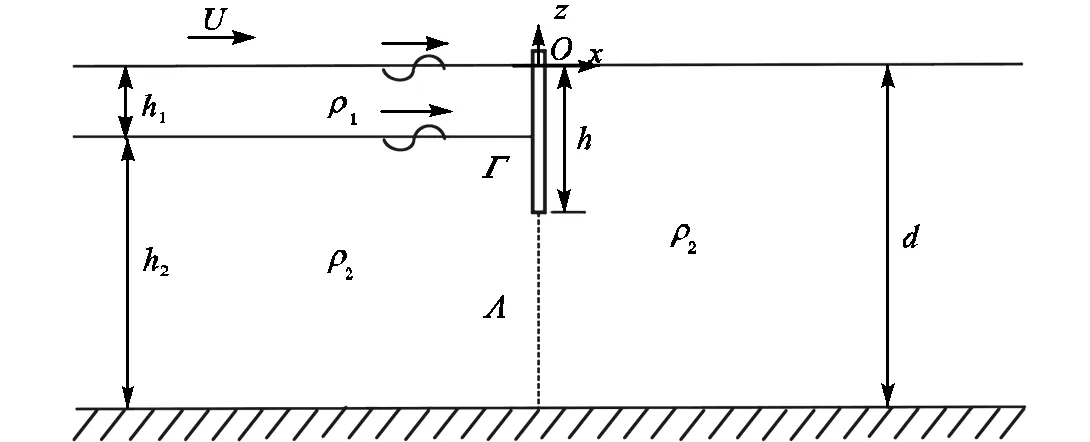
图3 波流作用区域划分示意

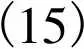
 (15)

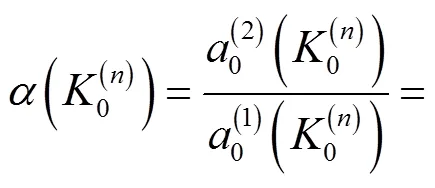
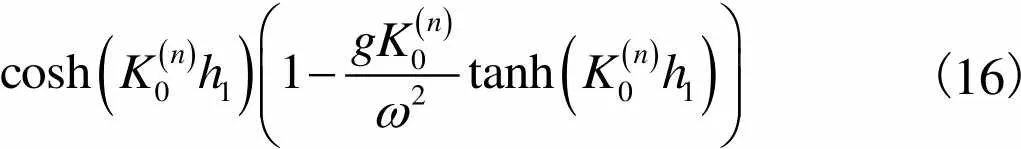
(16)

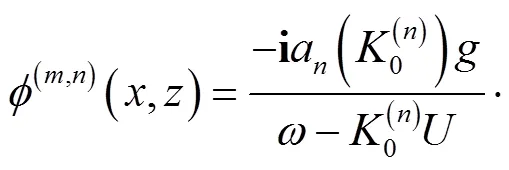
 (17)

式中＝1，2分别表示上、下层流体中的速度势．当波流同向时，取正值；波流异向时，取负值．

垂向特征函数为

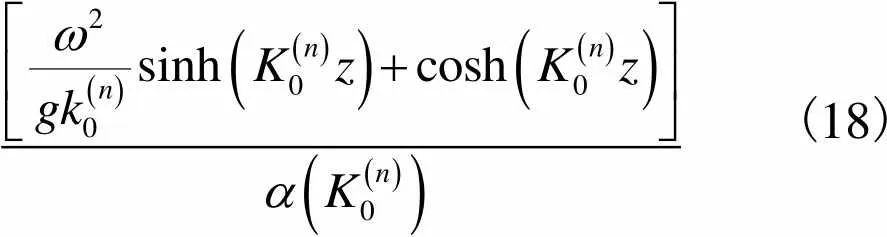
 (18)

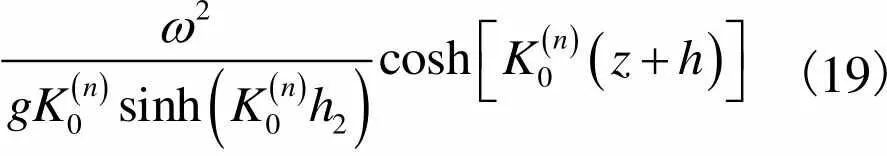
 (19)

当＝1时

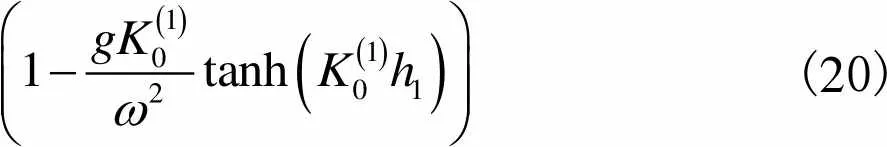
 (20)

当＝2时

 (21)

在迎浪侧，表面波模态速度势可用特征展开式表示为

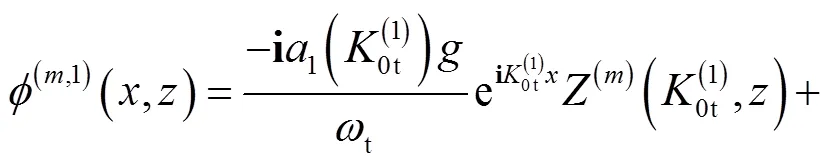
 (22)

2.2 背浪侧

背浪侧不存在油水分层情况，其色散关系为

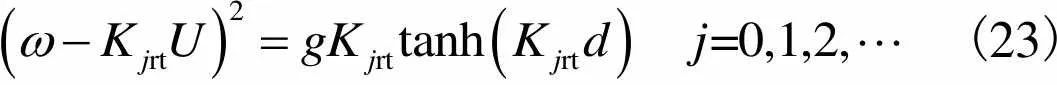
(23)

式中：Krt为考虑多普勒效应的背浪侧波数；0rt为式(23)的正实根；Krt(＝1，2，…)为式(23)的虚部为正的纯虚数根．当波流同向时，取正值；波流异向时，取负值．

背浪侧速度势可用特征展开式表示为

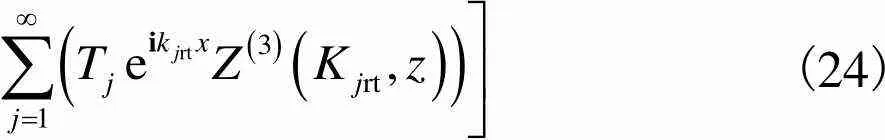
 (24)

式中求和号中多项式对应于振幅沿正向衰减的非传播模态扰动项．

垂向特征函数为

 (25)

2.3 问题的求解

在线性势流理论范畴内，波浪速度势()要求满足定解条件

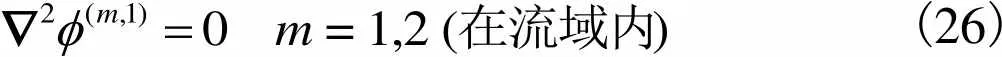
 (26)

,(27)

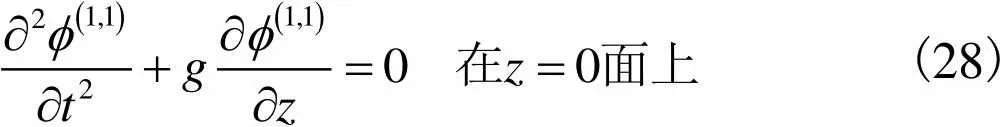
 (28)

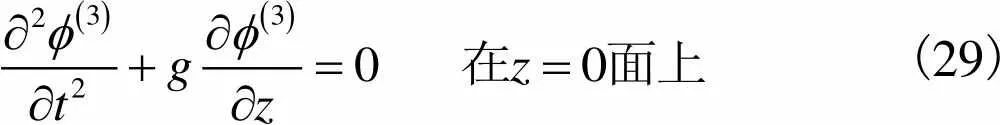
 ,(29)

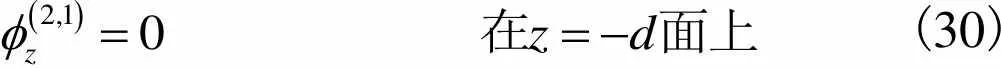
 (30)

  (31)

(32)

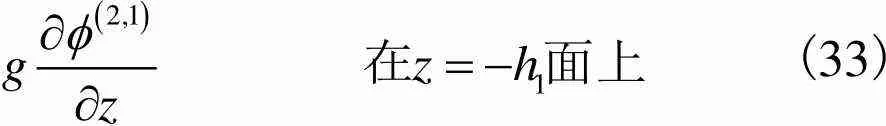
 (33)

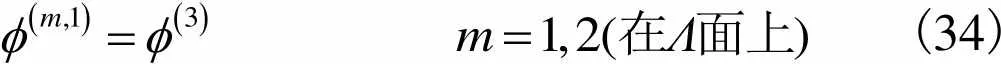
(34)

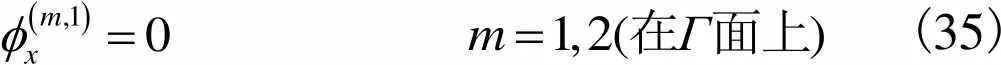
 (35)

(36)

根据式(34)及式(35)有

 (37)

 (38)

即

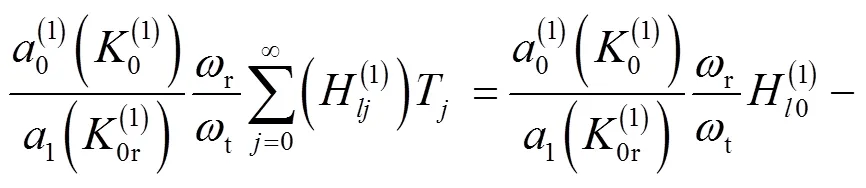
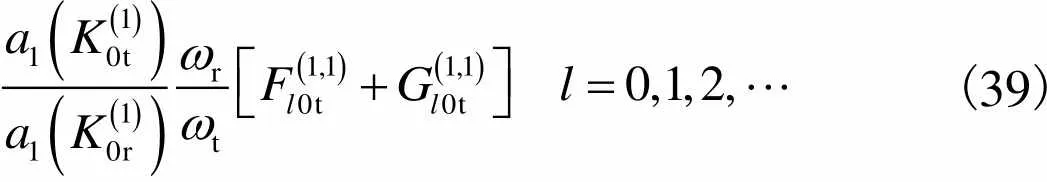
(39)

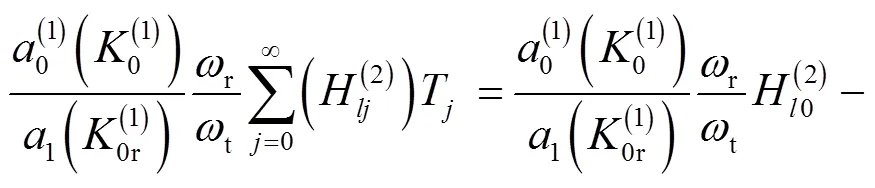
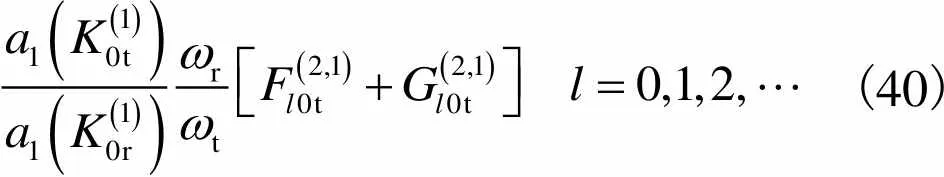
(40)

其中

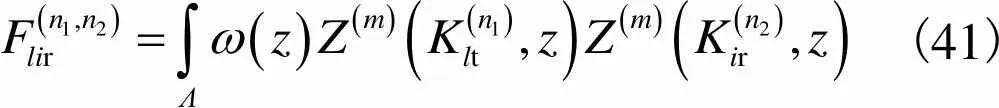
 (41)

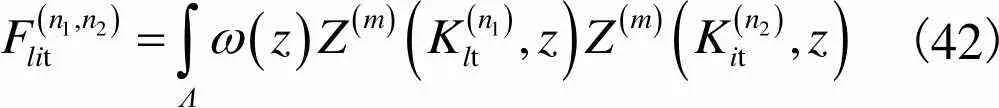
 (42)

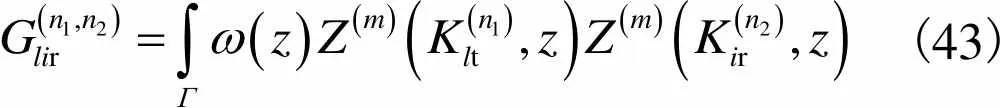
 (43)

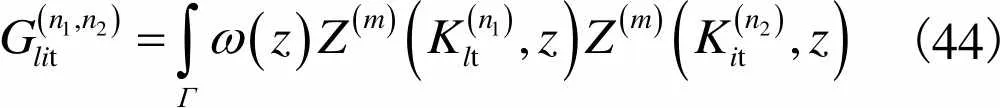
 (44)

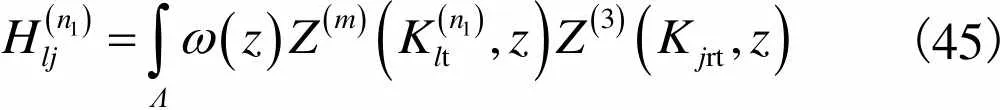
 (45)

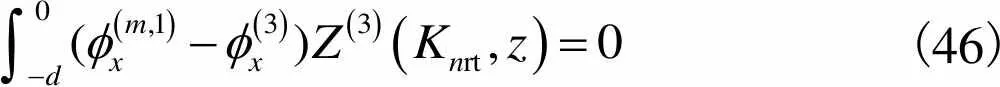
 (46)

即

(47)

其中

 (48)

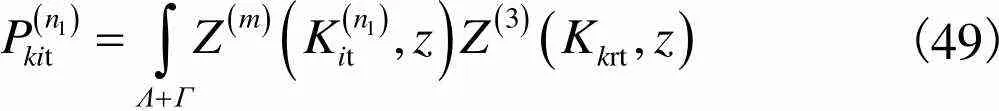
 (49)

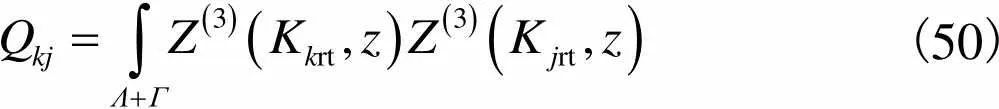
 (50)

对迎浪侧速度势的特征展开式取＋1项近似，对背浪侧速度势的特征展开式取＋1项近似后，利用式(39)、式(40)和式(47)可以得到2(＋1)＋＋1个关于R、r及T的线性方程组，进而得到波流作用下栏前压力结构．

对于波流作用下围油栏前液体压力由波流共存时伯努利方程确定，坐标系下波流共存时伯努利方程为

 (51)

假设距离围油栏上游无限远处液体压力忽略不计，为液体压力，wc为坐标系下考虑多普勒效应的整个流体速度势．

考虑到油膜单元的稳定性与当地静水压力关系不大，并忽略二阶速度势引起的倍频波流压力项．

在势流假设下，围油栏栏前液体压力可以表示为

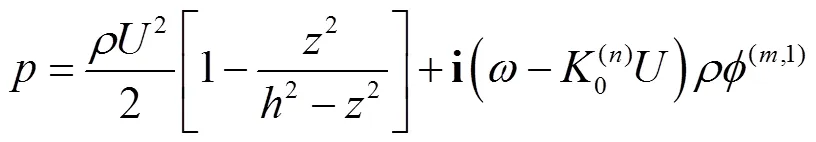
 (52)

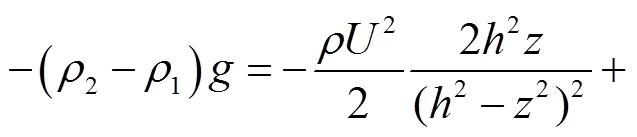
 (53)

将式(53)无量纲化可得

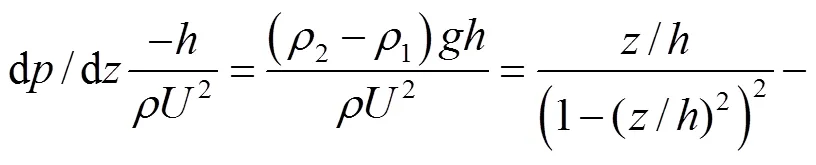
进而有

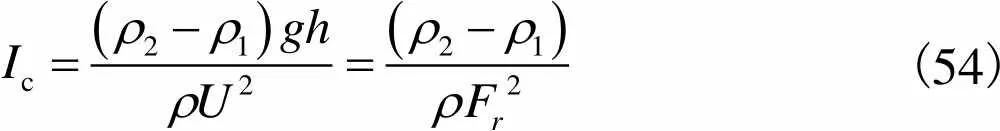
 (54)

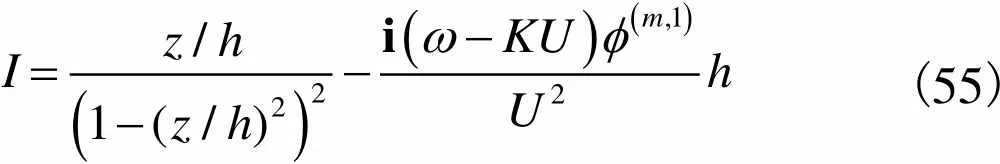
 (55)

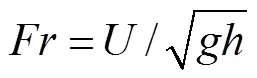
3 实验结果与分析

3.1 模型验证

为了检验数值模型的准确性，以Kordyban[5]实验为原型进行验证．Kordyban[5]的实验参数如下：入口流速分别为24.6和20.3,cm/s，水深分别为6.05和7.34,cm，围油栏吃水深度均为3.55,cm. Kordyban[5]的实验中没有报道油层性质，参考文献[7]报道油层厚度1=1,cm，油密度＝0.713,g/cm3.由图4可以发现，在纯水流作用下，分层流围油栏栏前液体压力垂直结构和Kordyban[5]实验值吻合．图5中，实线是用＝(/)(1-(/)2)-2计算得出，散点参考Kordyban实验，通过式(54)计算．可以发现纯水流作用下分层流围油栏临界稳定预测值和实验值 吻合．

图4 水流作用下液体压力垂直结构

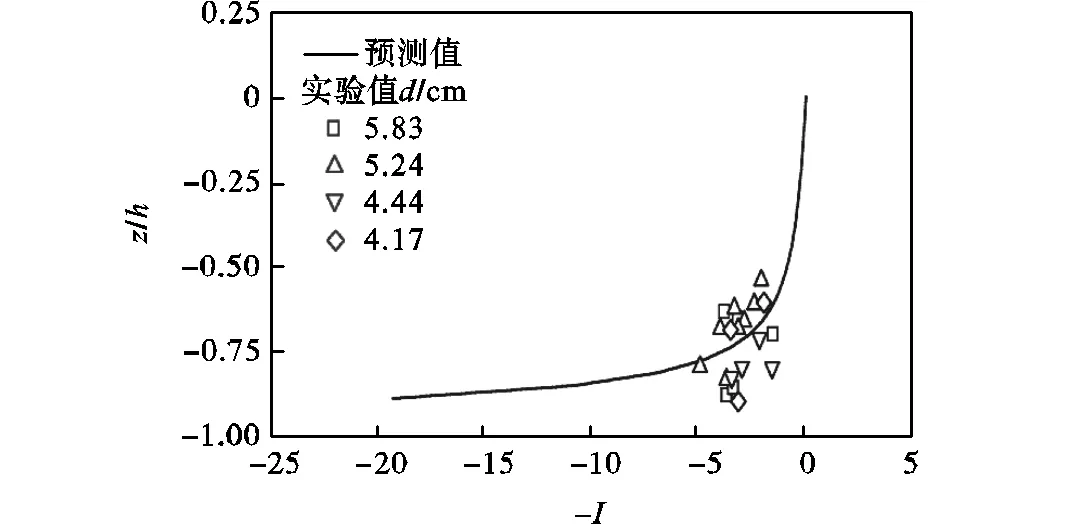
图5 水流作用下油水界面临界不稳定性指标

3.2 模型计算

3.2.1 流速的影响

波流作用下，水流速度不仅影响波浪传播形态，同时改变围油栏前的液体压力梯度，改变油水界面的稳定性．取流速＝0，5，10，15，20，25,cm/s，围油栏吃水深度＝20,cm，油层厚度1＝5,cm，表面波高＝5,cm，波周期为1,s，进行计算，波形如图6所示．

随着水流流速的增大，围油栏上游入射波和反射波偏差变大，其中入射波波长变长，波高变小，反射波波长变短，波高增大．选取一个波周期内，不同流速情况下围油栏前液体压力垂直结构进行分析，分别选取油水界面稳定性最不利情况(图7)，油水界面稳定性最有利情况(图8)．

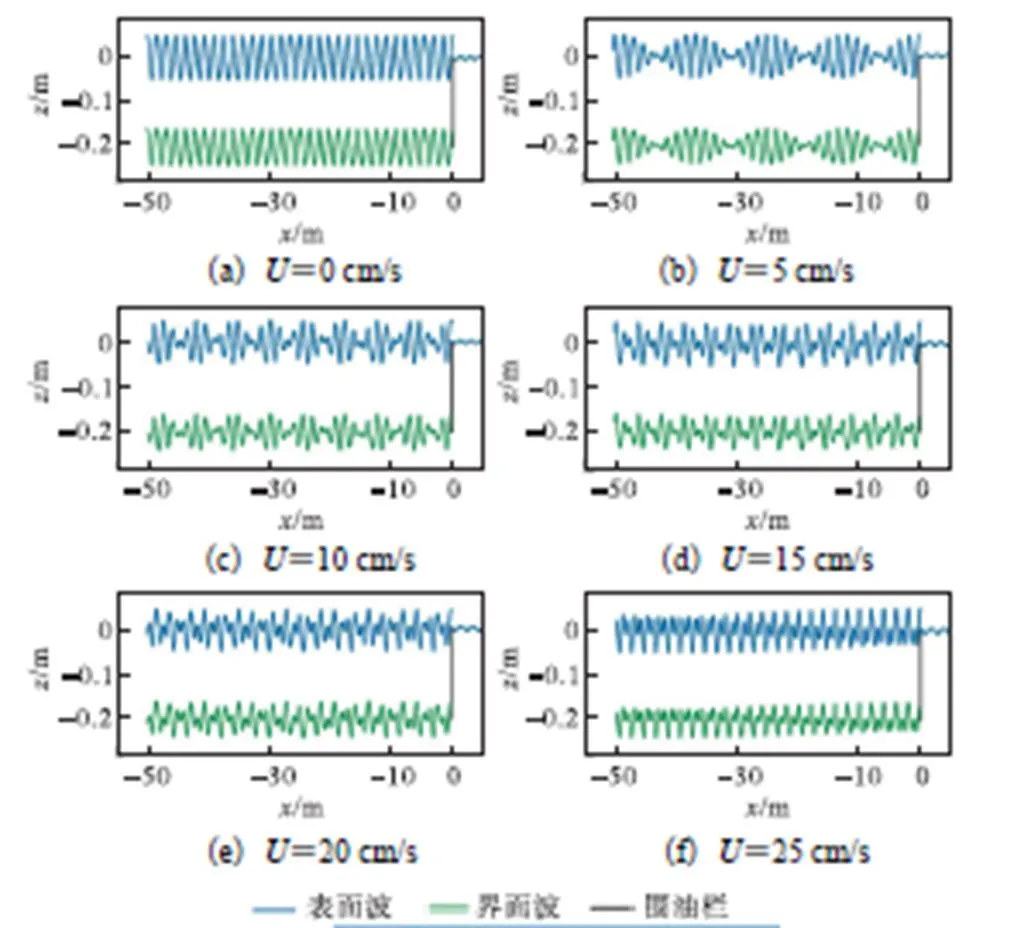
图6 不同流速下表面波、界面波波面形态

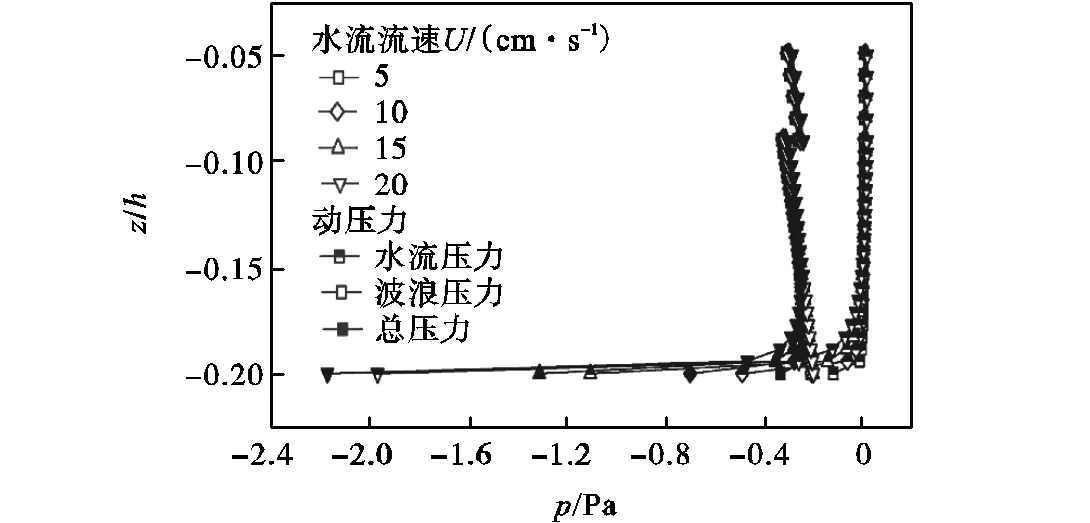
图7 最不利情况下流速对液体压力影响

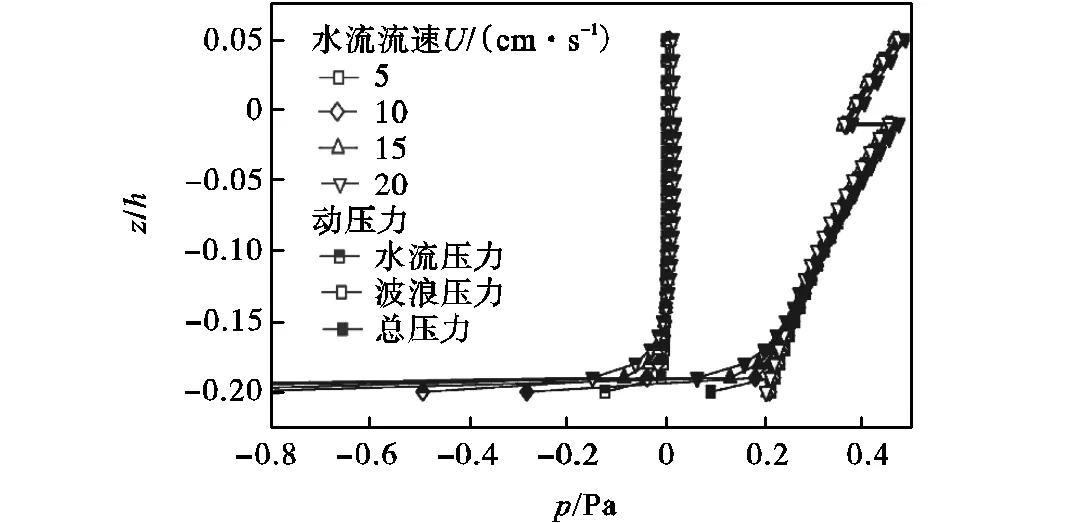
图8 最有利情况下流速对液体压力影响

通过比较发现，流速的增加会增大围油栏底部的液体压力梯度，其中不同水流大小对围油栏前液体压力垂直结构影响不大，相比水流作用引起的栏前动水压力，波浪对围油栏前液体压力结构的影响更为显著．当波峰逐渐传到围油栏处，栏前液体垂直压力梯度始终保持负值，油水界面稳定性处于不利情况，油滴有向下运动的趋势，油层厚度逐渐变大；当波谷逐渐传到围油栏处，栏前液体垂直压力梯度始终保持正值，油水界面稳定性处于有利情况，油滴有向上运动的趋势，油层厚度变小，这与Kordyban[5]所观察到的现象保持一致．由于栏前水位的变化可知，当波峰传到围油栏处时，栏前水位达到最大值，当波谷传到围油栏处时，栏前水位达到最小值，其栏前最大动水压力始终大于栏前最小动水压力的绝对值，即油膜经历一个波周期后总的趋势还是向下的，直到油水界面接近围油栏的底端，若此时波峰再次逐步传到围油栏处，油膜继续向下运动，则油滴将会越过围油栏发生油层流失失效．这可以解释Lee等[9]实验发现的有趣的现象：“一方面，水流流速＝31,cm/s、波高＝3.4,cm时，发生油层流失失效，同样的油品在纯水流环境下，水流流速达＝31,cm/s不会造成流失失效；另一方面，水流流速＝38,cm/s、波高＝1.4,cm时，不发生留有流失失效，同样的油品在纯水流环境下，水流流速达＝38,cm/s会造成流失失效”，Lee等[9]并没有给这一有悖于常理的现象作出解释，他认为波浪作用既可能增大初始失效流速，也可能减少初始失效流速．通过以上对波流作用下油水界面稳定性的分析，本文可以给出一个简要的解释：当波峰传到围油栏处时，栏前水位达到最大值，油滴往下运动，油层变厚，但是随着水位的升高，围油栏前的油滴运动越过围油栏发生失效的距离将会变长．反之，当波谷传到围油栏处时，栏前水位达到最小值，油滴往上运动，油层变薄，但是随着水位的降低，围油栏前油滴运动越过围油栏发生失效的距离将会变短，因此通过现有掌握的条件来判断围油是否失效远远不够．同时，考虑到围油栏有效吃水和有效干舷在波流作用在的运动响应，以及围油栏在水体中运动状态的复杂性，围油失效有着一定的随机性．但是可以肯定的是，波浪对栏前油水界面的影响是显著的，会极大地增加围油栏前油水界面的不稳定性，促使围油失效的产生．

由图9可见，当水流逐步增大时，总液体压力梯度线向水流压力梯度线逼近．即，波浪动压力梯度的影响逐渐减少，这可以解释Kordyban[5]观察到“当有波浪存在时，油水界面失稳较纯水流临界失稳要早，但是所测得的液体压力梯度却和纯水流作用下的栏前液体压力梯度差不多”．Kordyban[5]没有公布实验中油的密度和运动黏度，以及波浪要素．但是可以推断出Kordyban[5]文中关于波浪存在下的围油栏前液体压力分布是在流速较大的情况下测量得出的. 这给研究人员一个启示：相同波况条件下，水流流速较低时波浪动压力梯度占主导，栏前油水界面层处油滴会做周期性的上下沉浮运动，但这并不意味着只要波浪存在，一定会发生油层流失，因为这个时候围油栏也会做周期性的乘波运动，油水界面与围油栏并未发生较大的相对位移；在水流流速较大时，波流共同作用压力梯度线较之水流作用动压力梯度左偏，表明波浪的存在降低了油水界面稳定性标准，使得栏前油水界面更易失稳，发生围油失效．

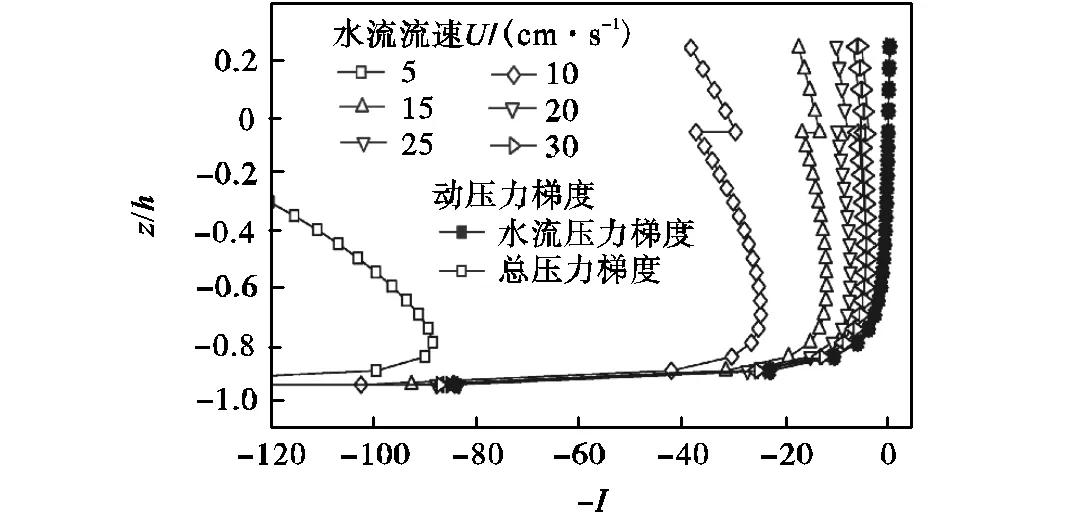
图9 流速对液体压力梯度影响

3.2.2 油水密度的影响

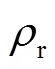
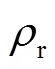
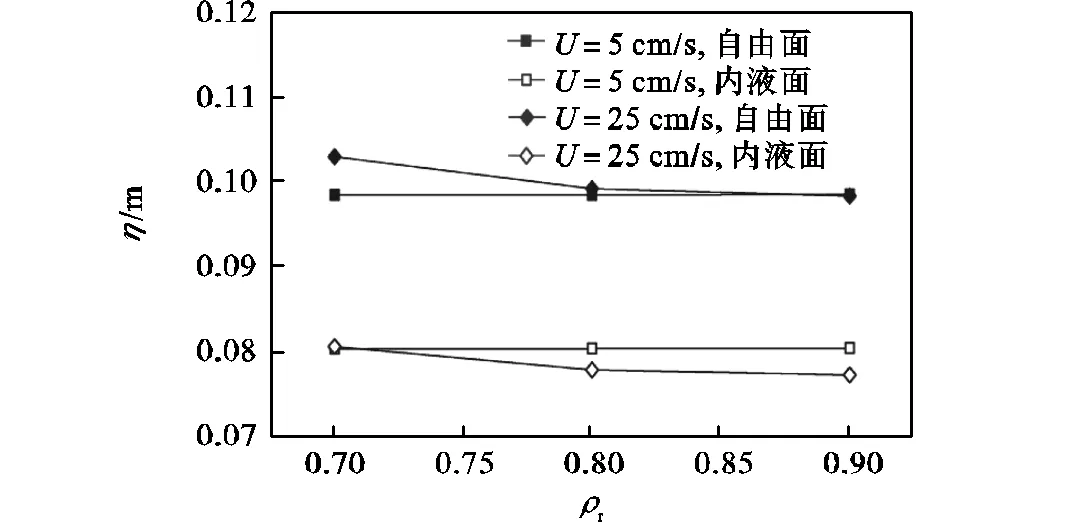
图10 油水密度对自由面、内液面波动影响

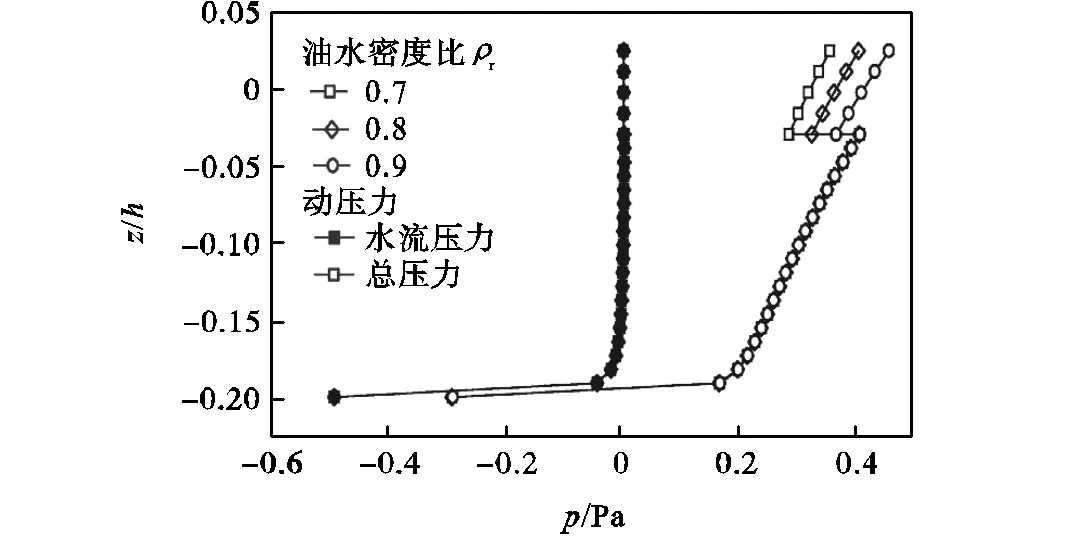
图11 油水密度对液体压力的影响

图12 油水密度对液体压力梯度的影响

3.2.3 油层厚度的影响

Amini等[11]发现波流作用下围油栏前发生油层流失失效很大程度上取决于初始油层的厚度，或者初始溢油体积，一般来说，增大初始溢油体积会减小拦油失效速度．已知，当水流速度较大时，波流共同作用下液体压力梯度趋于一致，因此为了探究油层厚度对栏前液体压力垂直结构的影响，取流速＝5，25,cm/s两种极限工况，围油栏吃水深度＝20,cm，油层厚度1＝5～15,cm，自由面波高＝5,cm，波周期为1,s，＝0.8进行计算．由图13可知，随着围油栏前油层厚度的增加，内液面波动逐渐减小，而自由面波动并没有显著变化．

图13 油层厚度对自由面、内液面波高的影响

由图14和图15可知，油层越薄围油栏受到的液体压力略有增加，改变油层厚度对围油栏前液体压力梯度影响不大．但是油水界面越低，距离围油栏底部的距离就越近．相同情况下，油水界面处的油滴就更容易越过围油栏失效．

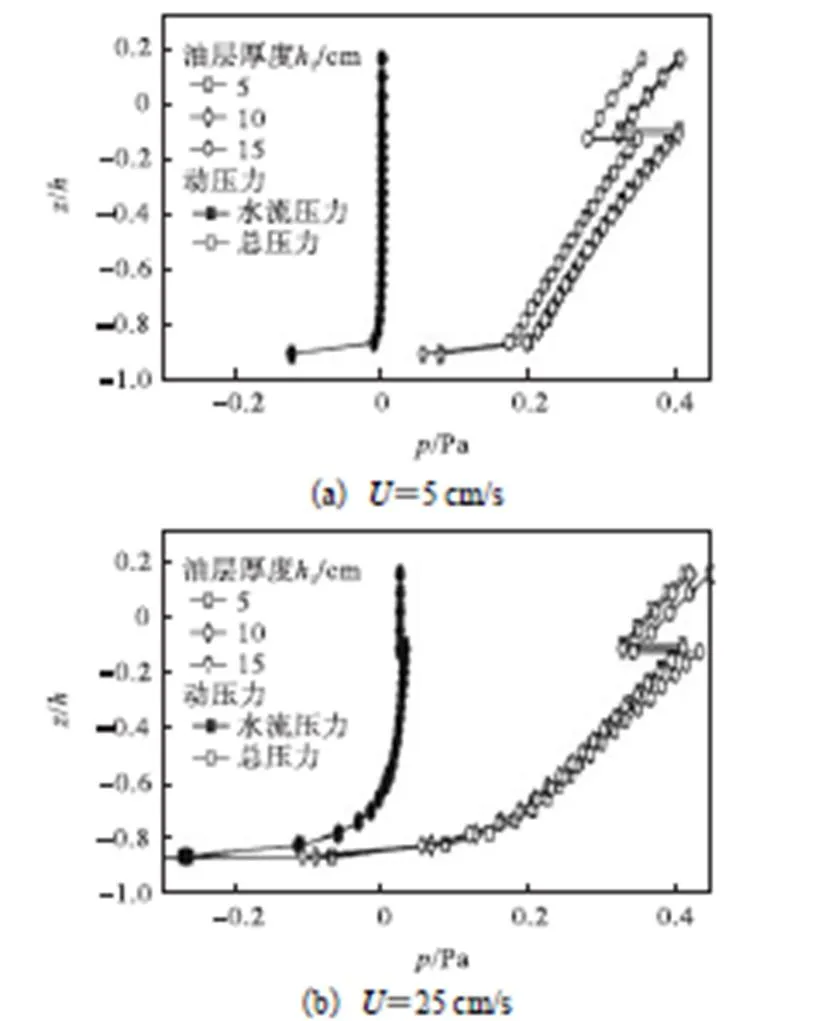
图14 油层厚度对液体压力的影响

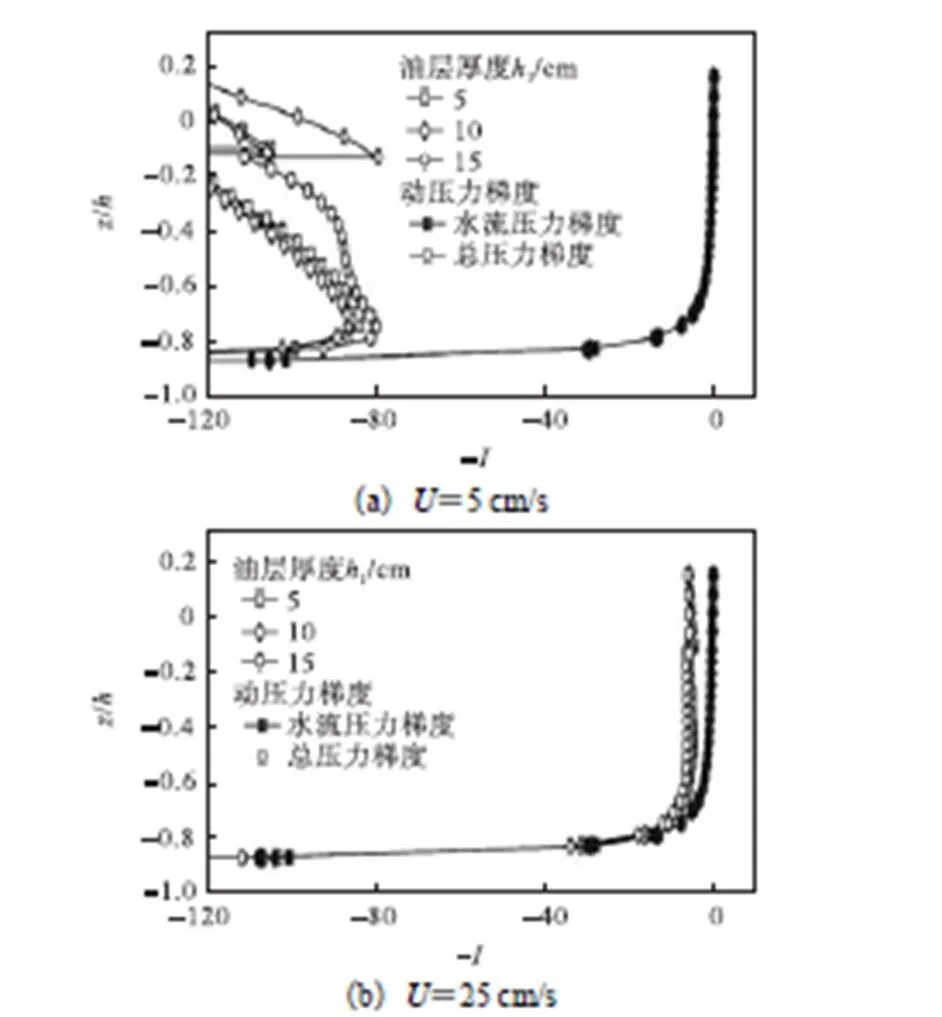
图15 油层厚度对液体压力梯度的影响

3.2.4 吃水深度的影响

Lee等[9]研究表明，围油栏吃水深度(有效栏深)增加，其抗浪流能力提高，拦油效果更好．由图16可见，对于5,cm厚的薄油层，围油栏深大于20,cm，自由面波高保持稳定值；围油栏深大于20,cm，内液面保持稳定值．即围油栏相对吃水深度(到对应液面的距离)超过油层厚度的4倍时，自由面、内液面波动将保持恒定．

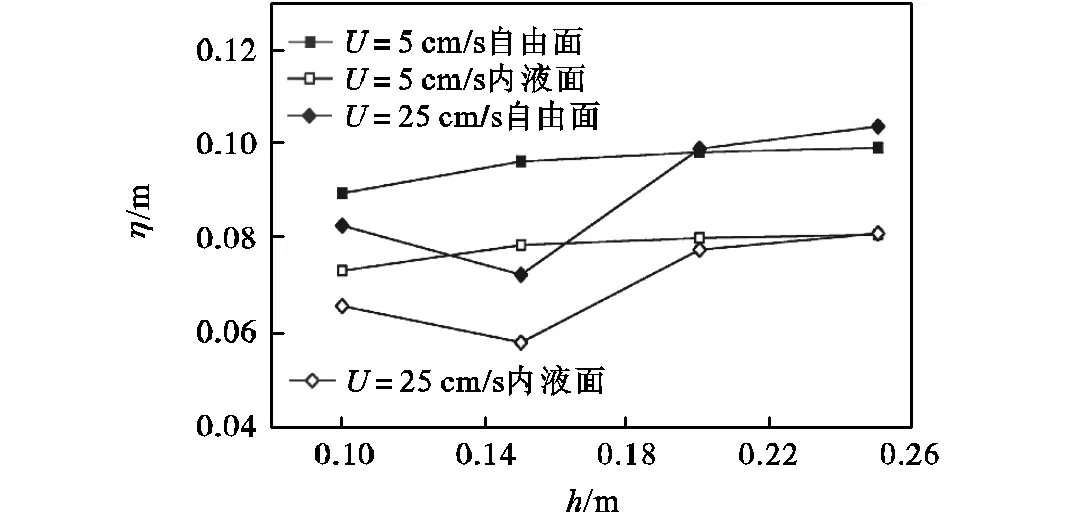
图16 吃水深度对自由面、内液面波高影响

式(54)表明，临界液体压力梯度与围油栏吃水深度呈正比，即围油栏吃水越大，抵抗油层流失的性能就越强，因此势流理论中围油栏吃水深度的增大会增加油水界面稳定性．由图17和图18可以看出，计算得出的围油栏前总液体压力梯度(界面处除外)与吃水深度也呈正比，因此仅通过栏前总液体压力梯度并不能作为判断油水界面是否稳定的依据．但是，注意观察到由于油水密度的不同，图17中油水界面上下层有一液体压力间断，当吃水深度增加时，虽然负液体压力梯度总体趋势表现出增加，但是界面处的正液体压力梯度同样增大．根据刘诚等[7]指出油水界面处的液体压力梯度才是判断油水界面稳定性的依据，可以得出吃水深度越大，油水界面越稳定．另一方面，由图17和图18可以看出，水流对波流作用下的栏前液体压力影响不大，但对栏前液体压力梯度则有显著影响．在高流速水域，增加围油栏栏深并不能有效增加围油栏滞油能力，这可以解释Castro等[12]通过物理实验得出的结论：“相比短裙摆围油栏而言，长裙摆围油栏有些时候并不能表现出优秀的滞油 能力”．

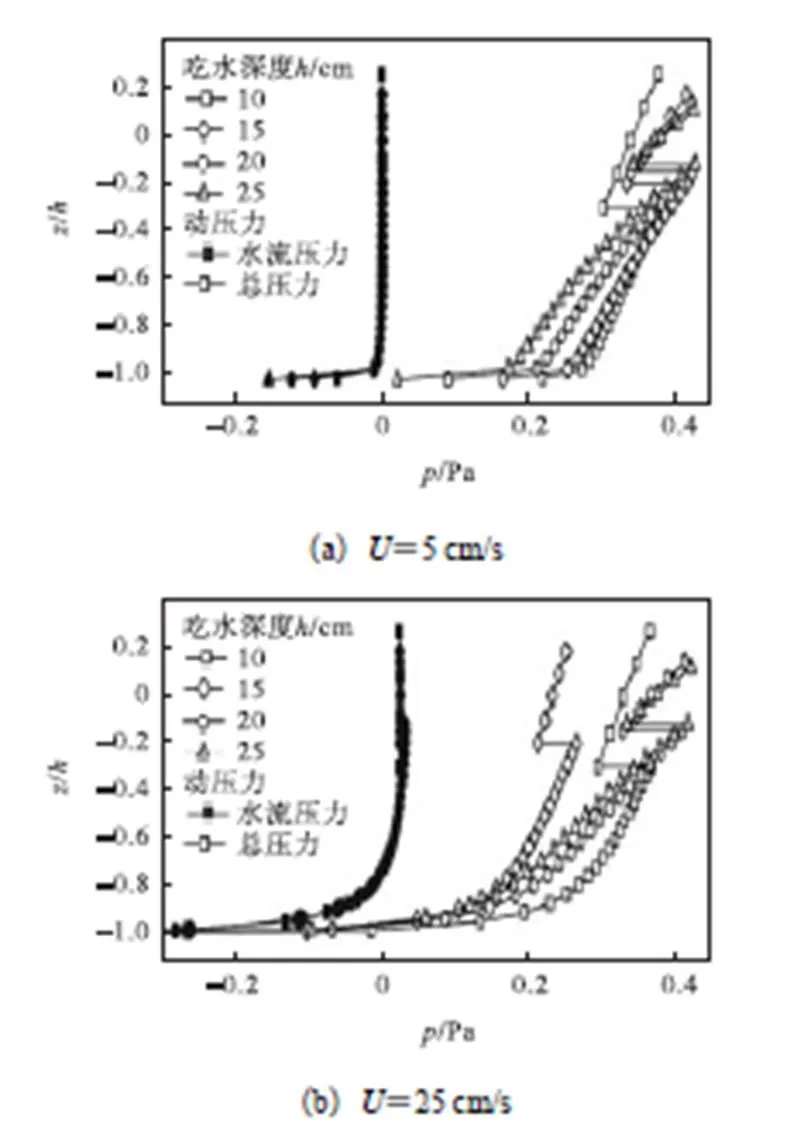
图17 吃水深度对液体压力的影响

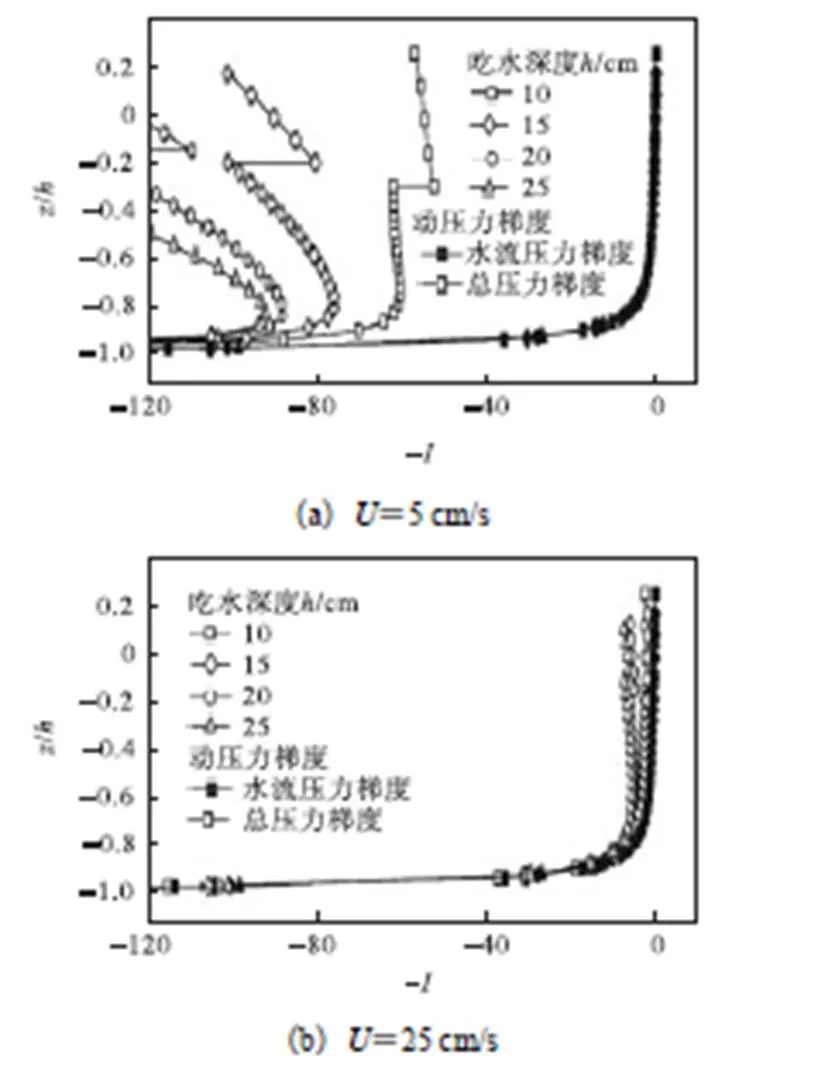
图18 吃水深度对液体压力梯度的影响

3.2.5 不同波况对油水界面稳定性指标的影响

当波峰传到围油栏栏前，波流结合稳定性指标左偏，意味当围油栏吃水深度和油品密度保持不变的情况下，油水界面更容易失稳，伴随着油滴向下运动以至越过围油栏发生围油失效．以下对比最不利条件下(波峰传到围油栏栏前)，不同波浪参数(见表1)对应油水界面失稳时的稳定性指标变化情况．

由图19可以看出，同周期波况情况下，油膜稳定指标与波高呈正相关，与波陡呈正相关；同表面波波高情况下，油膜稳定指标与波周期呈负相关，与波陡呈正相关．即同波数的波列，波形越陡油水界面越容易失稳；同波陡的波列，波数越大油水界面越容易失稳．且当水流条件增大时，不同波况对栏前液体压力梯度的影响差异性变小．

表1 波浪参数

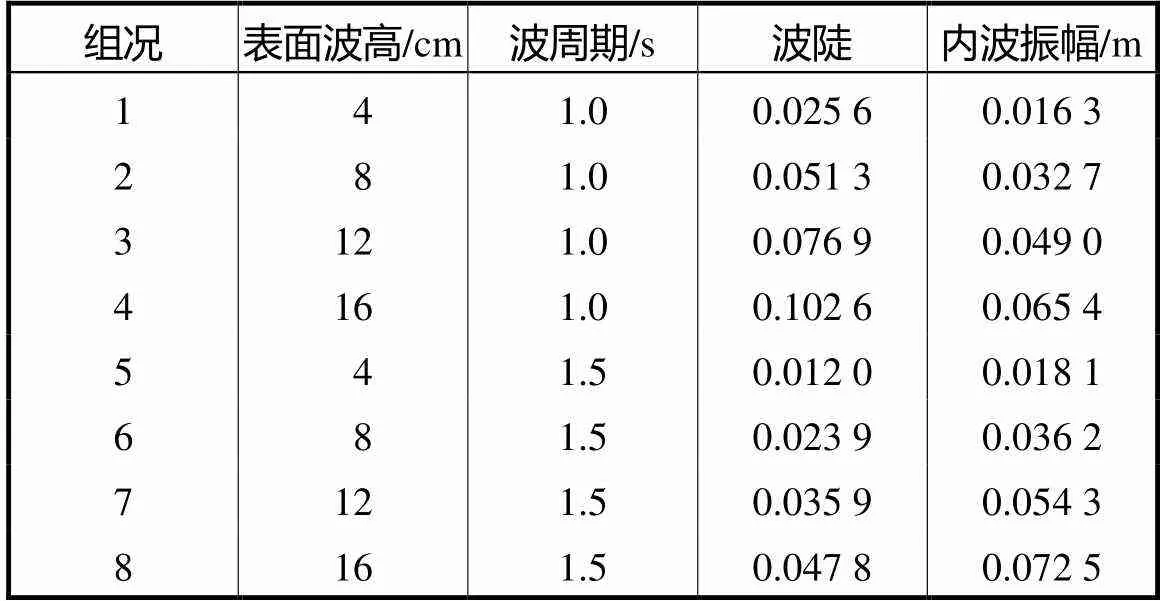
Tab.1 Wave parameters

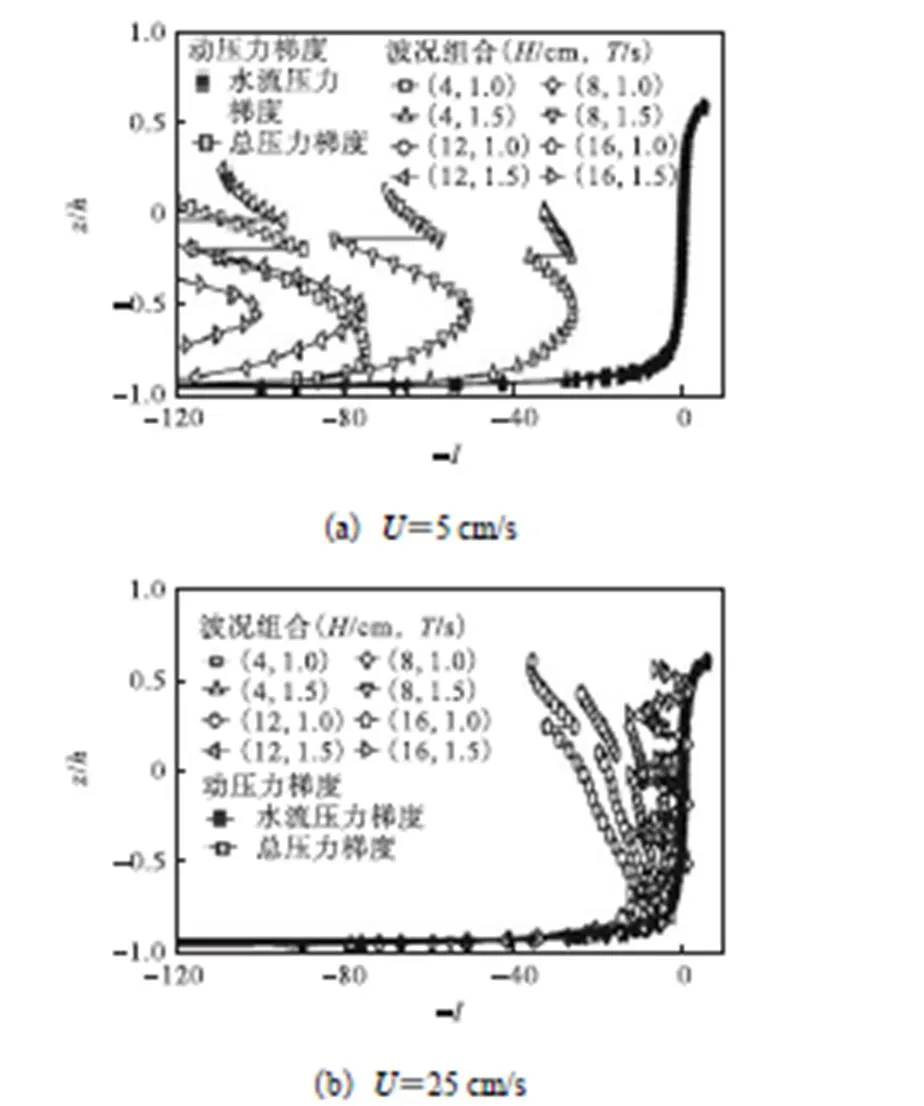
图19 波况对液体压力梯度的影响

通过波流共同作用下油水界面临界稳定条件，获取已知的水流、波浪条件可以确定围油栏最小吃水；也可以通过波浪条件以及围油栏、油品参数，确定实施围油布控的最大拖曳速度．Kordyban[5]测量了波流作用下栏前液体压力梯度(见图20)，并得到

 (56)

4 结 论

采用特征函数法研究油、水分层流体在围油栏栏前液体压力垂直结构，探讨了水流速度、油水密度、油层厚度、吃水深度以及不同波况对围油栏前溢油的运动及油水界面稳定性的影响．研究表明，围油栏前液体压力垂直结构决定了油水界面的稳定性．

(1) 水流流速大小对围油栏前液体压力垂直结构影响不大，但水流流速的增加会增大围油栏底部的液体压力梯度．相比水流作用引起的栏前液体压力，波浪对围游栏前液体压力结构的影响更为显著．当水流逐步增大时，波浪动压力梯度对油水界面稳定性的影响逐渐减小．波浪对油水界面的影响是周期性的，当波峰逐渐传到围油栏处，油滴有向下运动的趋势，油层厚度逐渐变大；当波谷逐渐传到围油栏处，油滴有向上运动的趋势，油层厚度变小．总的来说，波浪的存在降低了油水界面稳定性标准，栏前油水界面更易失稳发生失效．

(2) 油水密度比越大，界面处的液体压力梯度越大，栏前油水界面就越容易失稳．

(3) 油层厚度对围油栏前液体压力梯度影响不大．但是油水界面越低，距离围油栏底部的距离就越近，油水界面处的油滴就更容易越过围油栏失效．

(4) 围油栏吃水深度与无量纲液体压力梯度无关，油水界面处的液体压力梯度才是判断油水界面稳定性的依据．临界压力梯度与围油栏吃水深度呈正比，围油栏吃水深度越大油水界面越稳定．

(5) 同波数的波列，波形越陡油水界面越容易失稳；同波陡的波列，波数越大油水界面越容易失稳．当水流条件增大时，不同波况对栏前液体压力梯度的影响差异性变小．

［1］ Cross R H，Hoult D P. Collection of oil slicks[J].，，1971，97(2)：313-322.

［2］ Wilkinson D L. Discussion of collection of oil slicks[J].，，1972，98：122-125

［3］ Wilkinson D L. The dynamics of contained oil slicks[J].，1972，98：1013-1030.

［4］ Wicks M. Fluid dynamics of floating oil containment by mechanical barriers in the presence of water currents [C]//. American Petroleum Institute，America，1969：55-106.

［5］ Kordyban E. The behavior of the oil-water interface at a planar boom[J].，1990，112(18)：90-95.

［6］ Ertekin R C，Sundararaghavan H. The calculation of the instability criterion for a uniform viscous flow past an oil boom[J].，1995，117(1)：24-29.

［7］ 刘 诚，沈永明，梁 燕. 围油栏前压力垂直结构对油水界面稳定性的影响[J]. 中国科学：物理学力学天文学，2011，41(2)：170-177.

Liu Cheng，Shen Yongming，Liang Yan. Relationship between pressure gradient along the boom and the instability of oil-water interface[J].：，，2011，41(2)：170-177(in Chinese).

［8］ Amini A，Schleiss A J. Behavior of rigid and flexible oil barriers in the presence of waves[J].，2009，31(3)：186-196.

［9］ Lee C M，Kang K H. Prediction of oil boom performance in currents and waves[J].，1997，4(4)：257-266.

［10］ You Y X，Shi Q，Miao G P. The radiation and diffraction of water waves by a bottom-mounted circular cylinder in a two-layer fluid[J].，2007，19(1)：1-8.

［11］ Amini A，Bollaert E，Boillat J L，et al. Dynamics of low viscosity oils retained by rigid and flexible barriers[J].，2008，35(14/15)：1479-1491.

［12］ Castro A，Iglesias G，Carballo R，et al. Floating boom performance under waves and currents[J].，2010，174(1)：226-235.

(责任编辑：王新英)

Analysis of Instability of Oil-Water Interface Along the Oil Boom Under the Action of Waves and Currents

Shi Yang1，Li Shaowu1，Zhang Huaqin2，Chen Hanbao2，Zhou Ran2

(1．State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2．Tianjin Research Institute for Water Transport Engineering，Ministry of Transport，Tianjin 300456，China)

Oil spills resulting from maritime disasters can seriously influence the marine and coastal environment．Oil boom is widely used in collecting spilled oil．But its containment performance is seriously influenced by sea conditions，such as waves and currents．Boom failure is mainly induced by the instability of oil-water interface．The interaction between the water waves of the surface modes and a rigid boom in a two-layer fluid was theoretically examined by the eigen function expansion method．The hydraulic pressure gradient and the instability criterion were systematically investigated in terms of the specific gravity of oil，the thickness of oil slick，the boom draft，the current velocity and the wave condition．It is shown that the instability criterion is directly dependent on the vertical hydraulic pressure profile，and that the hydraulic pressure gradient near the oil-water interface is a dominant factor in instability criterion.

oil slick；oil boom failure；instability of oil-water interface；critical pressure gradient；eigen function expansion method

10.11784/tdxbz201707073

P751

A

0493-2137(2018)07-0691-11

2017-07-25；

2018-02-06.

时 洋（1993—），男，博士研究生，shiyang@tju.edu.cn

李绍武，lishaowu@tju.edu.cn.

国家自然科学基金创新研究群体科学基金资助项目(51321065)；国家国际科技合作专项资助项目(2015DFA90250)；国家自然科学基金资助项目(21677065).

the Science Fund for Creative Research Groups of the National Natural Science Foundation of China(No.,51321065)，Program of International S&T Cooperation(No.,2015DFA90250)and the National Natural Science Foundation of China(No.,21677065).