神经网络在经济市场波动率建模与预测中的应用

谢荣燕

(河海大学商学院，江苏 南京 211100)

0 引 言

股市市场的波动率建模与预测长期以来是经济学领域众多学者研究的重要课题。1980年以来，在波动率建模与预测研究中，通常应用基于低频数据的SV模型和GARCH模型来处理波动率建模与预测。1988年，Andersen和Bollerslev[1]使用非参数建模方法，提出了高频数据的波动率的度量方法。此后，Andersen等人[2-3]利用波动率的市场异质性和长记忆性，建立了HAR-RV模型。2010年，在已实现的波动率研究的基础上，文献[4]在GARCH模型和SV模型中加入已实现波动率作为其额外的解释变量，使用SPA检验进行评估，极大提高了模型的预测能力。

随着人工智能技术的发展，神经网络在各领域的应用越来越广泛。文献[5]提出了一种基于小波神经网络(WNN)预测模型，能够在短期内准确地预测风力发电，并适用于一年四季。文献[6]应用人工神经网络预测经济增长趋势。文献[7]利用人工神经网络模型对转型国家的GDP增长进行10年的预测。文献[8]使用递归神经网络对经济波动率进行了预测建模。文献[9]利用具有个体用户特征参数的非线性混合效应模型预测每日燃气需求量。文献[10]介绍了加拿大居民住宅能耗建模的神经网络(MLP)，并进行了条件需求分析和工程方法的比较。文献[11]提出一种基于多个经济指标的人工神经网络模型对韩国能源需求进行预测。文献[12]提出一种利用Cobbe Douglas函数的神经网络动态计量模型进行孟加拉的天然气需求的年度预测。有关人工神经网络在金融经济领域的研究可参考文献[13-17]。

基于前人的研究基础，本文提出一种新型马尔可夫交换人工神经网络，用于黄金市场的波动率建模和预测。

1 模型基础

马尔可夫交换模型在测试过程有一个特性，可以在资产价格内观察到波动的平稳性和转换过程。因此，本文结合马尔可夫交换(MS)和神经网络模型技术，使传统的ARMA-GARCH模型的预测精度得到更进一步的提高。在本文中，非线性的马尔可夫交换神经网络简称为MS-ARMA-GARCH-MLP模型，具体定义如下：

(1)

(2)

其中，i=1,…,m是不可观察的马尔可夫模型中不同的regimes。

(3)

(4)

(5)

式(3)～式(5)为模型数据的过滤概率式。如果转换概率P(st=i|st-1=j)被接受，则有：

(6)

当s→max {p,q}，递归程序由构造P(zs=i|zs-1)开始，其中，ψ(ztλh)是1/(1+exp (-x))形式的逻辑激活函数。神经网络模型的权重向量为ξ=w;ψ=g，输入向量被定义为ztλh=xi。如果转换概率P(zt=i|zt-1=j)被接受，则有：

f(yt|xt,zt=i)

(7)

同理，当s→max {p,q}，递归程序由构造P(zs=i|zs-1)开始。式(2)给定的模型可以改良为马尔可夫交换APGARCH模型，简称MS-ARMA-APGARCH-MLP模型，定义为：

(8)

其中，t=1,…,m是不可观察的马尔可夫模型的regimes，式(3)通过式(9)定义改进人工神经网络模型MS-ARMA-APGARCH-MLP，其激活函数为ψ(ztλh)。如果δ=2和γk=0，MS-ARMA-APGARCH-MLP模型就变成了MS-ARMA-GARCH-MLP模型。类似地，如果γk=0，模型就变成MS-ARMA-GARCH-MLP模型，而当δ=2和0γk1，则变成MSGJRGARCH-MLP模型。当δ=1和0γk1，则该模型就变成了MSTAGRCH-MLP模型。MS-ARMA-FIAPGARCH模型是MS-ARMA-FIAPGARCH-MLP的神经网络的增广模型，该模型的条件方差定义为：

=-(1-φ(st)L)(1-L)d(st)(|εn-1,st|-γk,(st)εn-1,st)δ(st)+

(9)

其中，激活函数h为sigmoid形式的神经元，式(9)定义了MS-ARMA-FIAPGARCH-MLP模型，该模型是MSAGARCH-MLP神经网络模型的变体，激活函数定义为ψ(ztλh)。类似地，当δ(st)=2和γk,(st)=0，该模型就转化为MSFIGARCH-MLP模型。当δ(st)=2和0γk,(st)1，该模型转化为MSFIGJRGARCH-MLP模型。当δ(st)=1和0γk,(st)1，该模型即为MSTGARCH-MLP模型。

此外，该模型可以表示分数阶积分参数限制下的短时记忆的特点。当通过把d(st)=0转接到分数阶积分参数，式(10)则转化为MS-ARMA-APGARCH-MLP模型。一个典型例子，考虑如下MS-ARMA-APGARCH-MLP模型：

= -(1-φ(1)L)(1-L)d(1)(|εn-1|-γk,(1)εn-1)δ(1)+

= -(1-φ(2)L)(1-L)d(2)(|εn-1|-γk,(2)εn-1)δ(2)+

(10)

随着马尔科夫回归空间的分裂，模型允许有2个不同的动力项δ(1)和δ(2)以及2个不同的分数阶积分参数。因此，在2个不同的制度下，允许有不同的长期记忆和不对称的动力结构。当t=1时，神经网络NN-FIAPGARCH模型定义为：

= ((1-βL)-(1-φL)(1-L)d)(|εn-1|-γk,(1)εn-1)δ+

(11)

如果t=1和δ(s1)=δ=2，则有：

= ((1-βL)-(1-φL)(1-L)d)(|εn-1|-γk,(1)εn-1)2+

2 经济数据仿真

为了验证上述模型的预测性能，本文进行了相应的仿真实验。在中国黄金的回报是以收盘价格计算，为了获得收益数据，数据计算如下：y=ln (Pt/Pt-1)。其中ln (·)是自然对数，是股票收益的度量标准。在数据训练的过程中，样本分成训练集、测试集和样本外的数据集3个部分，各占比例为80%、10%、10%。

在表1中，对跃迁矩阵和MS模型进行了计算，Regime1和Regime2的标准偏差值分别为0.05287、0.014572。在Regime1中，其持续了大约75.87个月，在Regime2中，其持续了大约107.61个月。采用最大似然法，MS-GARCH模型假设其误差随Student-t分布。因此，在MS-GARCH模型估算中，假设必须符合t分布。该模型的转变概率的计算为P(st=1|st-1=1)=0.5，结果显示，该模型的持久性较低。

表1 传统经济学预测方法

1.MS-GARCHarchgarchsigmaconstantlogLRMSERegime10.03351(0.005)***0.563870.966483(0.01307)***0.4361240.000333727(1.916e-006)***0.00043566.23008e-005(1.360e-005)***6.29344e-005Regime2(0.0098)***(0.01307)***(1.231e-005)***(1.161e-005)***385.090.458912.MS-APGARCHarchgarchsigmaconstantlogLRMSERegime10.383241(0.0102)***0.02010.616759(0.0130)***0.7919500.000679791(5.68E-006)***0.00123818.13394e-005(2.007e-005)***8.20782e-005Regime2(0.0201)***(0.01307)***(3.41e-004)***(1.835e-005)***1756.50.421113.MS-FIAPGARCHarchgarchd-figarchAparchlogLRMSERegime10.277721(0.00)***0.3093850.67848(0.00)***0.6806150.2761233(0.0266)***0.1815420.220157(0.0106)***0.21083Regime2(0.002)***(0.0001)***(0.00005)***(0.0299)***1877.90.42220

另一方面，值得关注的是，通过改进转移概率到regime转换的条件波动性建模，其所期望的结果并没有得到。MS-GARCH模型通过MLP、RBF和RNN模型进行结合扩展使用，下面测试其建模性能。

在MS-GARCH-NN神经网络模型研究中，模型的计算是利用反向传播算法和相对于平方损失函数聚集的参数更新；反之，则使用权重与权重衰减迭代的计算方法来实现最低的预测错误。MS-GARCH-NN神经网络模型的训练样本的MSE和RMSE值的比较如表2所示。

表2 MS-GARCH-NN神经网络训练样本结果

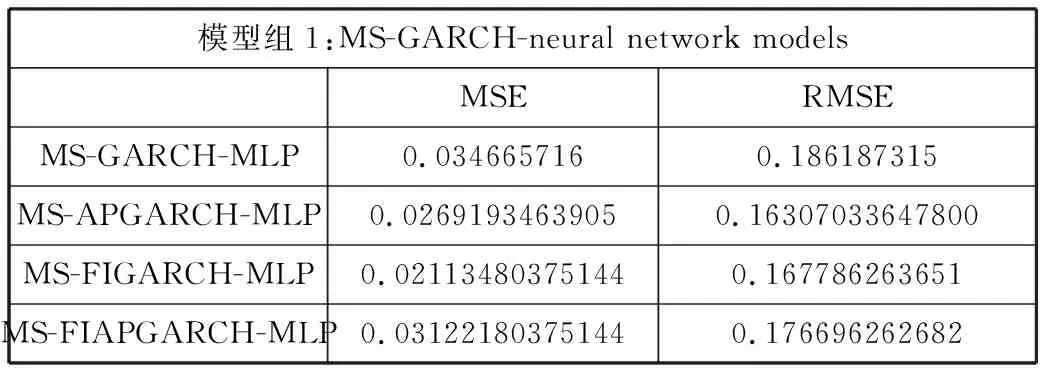
模型组1:MS-GARCH-neural network modelsMSERMSEMS-GARCH-MLP0.0346657160.186187315MS-APGARCH-MLP0.02691934639050.16307033647800MS-FIGARCH-MLP0.021134803751440.167786263651MS-FIAPGARCH-MLP0.031221803751440.176696262682

在表3中，有4种不同模型下训练样本的MSE和RMSE值，如模型MS-APGARCH-MLP、MS-FIGARCH-MLP、MS-FIAPGARCH-MLP。接下来，4种神经网络模型下的测试样本的结果如表3所示。

表3 MS-GARCH-NN神经网络测试样本结果

模型组1:MS-GARCH-neural network modelsMSERMSEMS-GARCH-MLP0.0153333780.123828017MS-APGARCH-MLP0.0000000133337910.0001154898313MS-FIGARCH-MLP0.0000000139225650.0001345775142MS-FIAPGARCH-MLP0.00000001389430.00011787886146

表4 样本外数据的神经网络预测结果

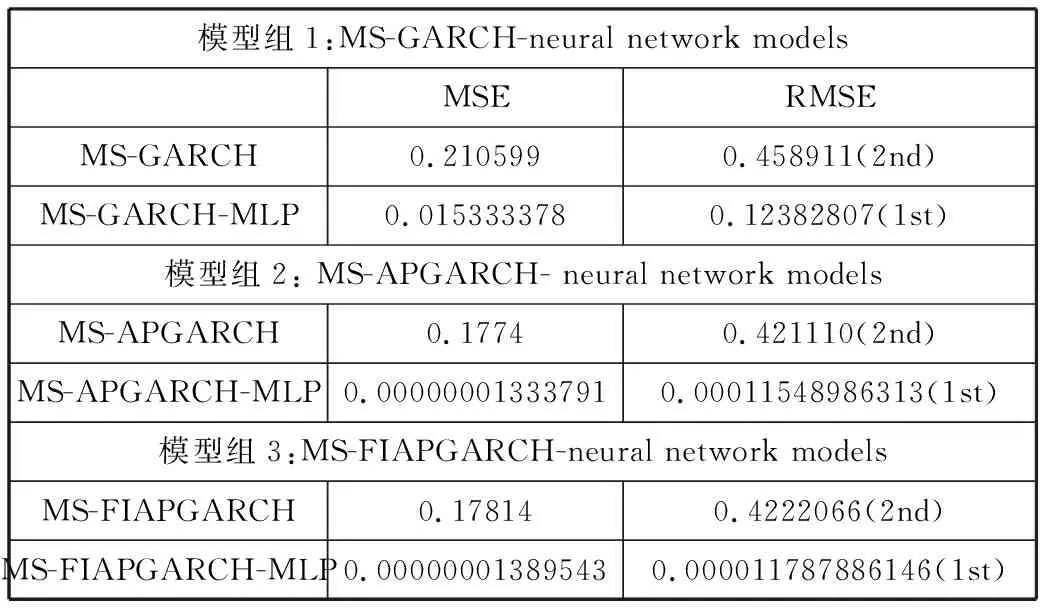
模型组1:MS-GARCH-neural network modelsMSERMSEMS-GARCH0.2105990.458911(2nd)MS-GARCH-MLP0.0153333780.12382807(1st)模型组2: MS-APGARCH- neural network modelsMS-APGARCH0.17740.421110(2nd)MS-APGARCH-MLP0.000000013337910.00011548986313(1st)模型组3:MS-FIAPGARCH-neural network modelsMS-FIAPGARCH0.178140.4222066(2nd)MS-FIAPGARCH-MLP0.000000013895430.000011787886146(1st)

值得注意的是，从MS-GARCH-NN模型到MS-APGARCH-NN和MS-FIGARCH-MLP模型的分数阶积分整合过程中，MS、GARCH和ANN的混合模型的收益值有相对大的浮动，更不容忽视的一点就是，为了使结果更加精确，除了对训练样本进行改进，测试样本和样本外的抽样数据的选取也同样重要。在表3的测试样本结果中，第一个模型的测试结果为RMSE=0.1238，而其值最小的为MS-APGARCH-MLP模型，为RMSE=0.00011548。由此可见，从MS-GARCH-MLP神经网络到MS-APGARCH-MLP神经网络模型，其预测能力得到了极大提高。

样本外的数据预测结果如表4所示。在表4中，可以看到，相比传统经济学上的MS-GARCH、MS-APGARCH、MS-FIAPGARCH模型的预测，人工神经网络的预测更为精确，预测性能得到极大的提高。在模型组1中，MS-GARCH-MLP神经网络相对于传统的MS-GARCH的预测性能提升不大，但在MS-APGARCH-MLP和MS-FIAPGARCH-MLP神经网络中，其MSE和RMSE值的级数远远小于传统的MS-APGARCH和MS-FIAPGARCH的预测值，即其预测误差远远小于传统经济预测方法，因此，应用神经网络来解决黄金市场的波动率建模与收益预测更具有现实的应用价值。

3 结束语

本文对4类马尔可夫交换增广神经网络的波动率建模和黄金收益预测进行了讨论，并从黄金股市的股票指数的绝对误差(MAE)、均方误差(MSE)和均方根误差(RMSE)数据进行了仿真分析，表明了本文算法的有效性。在经济市场的波动率建模和预测研究方向，本文从传统的MS-GARCH预测模型，推广到结合MLP、RBF和ARR的MS-APGARCH-MLP和MS-FIAPGARCH-MLP神经网络模型，为今后神经网络在经济方向的研究提供了重要的参考。

参考文献：

[1] Andersen T G, Bollerslev T. Dm-Dollar volatility: Intraday activity patterns, macroeconomic announcements and longer run dependencies[J]. Journal of Finance, 1988,53(1):219-265.

[2] Andersen T G, Bollerslev F X. Modeling and forecasting realized volatility[J]. Econometrical, 2003,71(2):579-625.

[3] Corsi F. A simple approximate long-memory model of realized volatility[J]. Journal of Financial Econometrics, 2009,7(2):174-196.

[4] 魏宇. 沪深300股指期货的波动率预测模型研究[J]. 管理科学学报， 2010,2010(2):66-76.

[5] Abhinav R, Naran M P, Wu J Z, et al. Short-term wind power forecasting using wavelet-based neural network[J]. Energy Procedia, 2017,142(1):455-460.

[6] Feng Lihua, Zhang Jianzhen. Application of artificial neural networks in tendency forecasting of economic growth[J]. Econometrical Model, 2014,40(C):76-80.

[7] Libor Krkoska, Utku T. Accuracy of GDP growth forecasts for transition countries: Ten years of forecasting assessed[J]. Econometrical System, 2009,33(1):386-388.

[8] Tino P S, Dorffner C G. Financial volatility trading using recurrent neural network[J]. IEEE Transactions on Neural Network, 2001,12(4):865-874.

[9] Brabec M, Konar O, Pelik E. A nonlinear mixed effected model for the prediction of natural gas consumption by individual customer[J]. International Journal of Forecasting, 2008,24(1):659-678.

[10] Aydinalp-Koksal M, Ugursal V. Comparison of neural network, conditional demand analysis, and engineering approaches for modeling enduse energy consumption in the residential sector[J]. Applied Energy, 2008,85(1):271-296.

[11] Geem Z W, Roper W E. Energy demand estimation of South Korea using artificial neural network[J]. Energy Policy, 2009,37(5):4049-4054.

[12] Wadud Z, Dey H S, Kabir M. Modeling and forecasting demand in Bangladesh[J]. Energy Policy, 2011,39(1):7372-7380.

[13] Alma Y A. Electricity prices forecasting using artificial neural network[J]. IEEE Latin America Transactions, 2018,16(1):105-111.

[14] Kada A, Youlal H. E-financial secure solution using neural network techniques[J]. Canadian Journal of Electrical and Computer Engineering, 2005,30(3):145-148.

[15] Xu Zhiping. Modeling and simulation of financial crisis warning system based on RBF neural network[C]// 2016 International Conference on Robots & Intelligent System (ICRIS). 2016:264-267.

[16] Ramadhan G, Arian D, Surjandari I, et al. Application of artificial neural network for predicting company financial performance in Indonesia stock exchange[C]// 2017 3rd International Conference on Science in Information Technology (ICSITech). 2017:241-245.

[17] Ma Chi, Lin Junnan, Sun Hongyan, et al. A hybrid financial time series model based on neural networks[C]// 2017 8th International Conference on Intelligent Control and Information Processing (ICICIP). 2017:303-308.