一类周期均值回复过程的最小二乘估计

,

(蚌埠学院理学院，安徽 蚌埠 233000)

0 引 言

经典Ornstein-Uhlenbeck 过程(以下简称O-U过程)的特点是经一段时间的演化后会回归到长期均衡水平，这个特点被人们称为均值回复.正因为这个特点使得O-U过程在物理、金融等领域有着广泛的应用[1-2]. 近些年来，关于O-U过程漂移项未知参数的统计推断问题已被很多学者深入研究[3-8]. 这些文献大多假定O-U过程带有常数回归水平且过程是遍历的。然而，实际问题中有些数据含有季节因素或长期趋势，此时仅带有常数均值水平的O-U过程就不能用来拟合这些数据了. 因此，Bishwal[9]，Dehling等人[10]， Franke和Kott[11]考虑一类推广的O-U过程，其漂移项带有时间函数.本文要研究的正是这类均值回复过程，还进一步假定漂移项中的时间函数是周期函数，并称此类均值回复过程为周期均值回复过程. 到目前为止，国内外关于周期均值回复过程的统计推断的研究文献非常少，Dehling等人在文献[10]中构造了一个周期均值回复过程未知参数的极大似然估计量，并证明了该极大似然估计量具有强相合性和渐近正态性.基于连续样本轨道，本文构造了一类周期均值回复过程未知参数的最小二乘估计量，该估计量与文[10]中极大似然估计量相比，构造时无需附加一些条件.还论证了此最小二乘估计量具有强相合性；估计误差的渐近分布研究是随机微分方程参数估计问题的一大难点，借助一个中心极限定理[14-15]证明了估计误差的渐近正态性，该证明比文献[10]中的证明简单.

1 最小二乘估计量构造

假设(Ω,F,Ρ)是一个完备的概率空间，B是定义在该空间上的标准布朗运动.主要考虑一类周期均值回复过程{Xt,t≥0}满足如下的随机微分方程：

dXt=(F(t)-βXt)dt+dBt,t≥0

(1)

为了估计方程(1)中的未知参数，需对方程(1)作如下假设：

(A1)设L(θ,t,Xt)=F(t)-βXt，L(θ,t,Xt)满足全局Lipschitz条件和线性增长条件.

(A2)设θ0=(α1,α2,…,αm,β)*，α1,α2,…,αm,β是参数的真实值.

(A3)设f1(t),f2(t),…fm(t)在实数集R的紧区间上是有界的.

(A4)设f1(t),f2(t),…fm(t)具有同周期l的周期函数，即fi(t+l)=fi(t).

其中假设(A2)中的(·)*表示一个向量的转置.

为了计算的方便，假定样本数据的观测时间长度T是周期l的整数倍即T=Nl,N是整数.而且不失一般性，令周期l等于1. 接下来，在上述假设基础上来构造方程(1)中未知参数的最小二乘估计量并讨论其相关的统计性质.

设随机过程{Xt,t≥0}在[0,T]上能被连续观测，引入下面的比较函数：

(2)

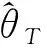
(3)

其中

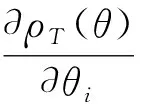
上面的线性方程组可简写成：

因条件(A4)和(A5)成立，则GT=TIm. 再由线性方程组求解知

命题1.1得证.

注1.1 一般情况下，矩阵PT不一定是可逆的，但当观测时间T足够大时PT是可逆的.并且矩阵PT的逆可通过分块矩阵求逆的方法得到，详细求逆过程可参见文献[10].矩阵PT的逆可表达为:

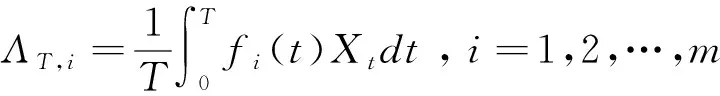
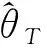
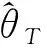
2 最小二乘估计量的强相合性及渐近正态性证明

Xt=e-βtx0+g(t)+Z(t)

(4)

其中

(5)

引理2.1[10]定义在C[0,1]上的随机变量序列

(6)

是平稳的、遍历的.

引理2.2[10]当t→∞，则有

(7)

现应用方程(1),可将式(3)重写可得到命题2.1.

命题2.1 如果{Xt,0≤t≤T}的样本轨道能被连续观测，且条件(A4)和(A5)成立，则有

(8)

证明： 事实上，根据方程(1)知

亲爱的同学们，大家好！这一期的“我是小编辑”活动组来到了安徽省合肥市肥东县光彩希望小学，让我们来看看严冬老师和他的学生们带来的作品吧！

则有

和

那么矩阵QT可写成：

其中

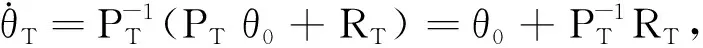
命题2.1得证.

命题2.2 如果{Xt,0≤t≤T}的样本轨道能被连续观测且条件(A4)和(A5)成立，则当T→∞.

对于,命题2.2的证明，需应用一个多重随机积分中心定理即引理2.3，这个引理的详细证明参见文献[14]或[15].

引理2.3 设Ip(fT),T≥0是一列p(p≥2)阶重积分，满足

则下面两个断言等价：

(ⅰ)当T→∞时，Ip(fT)依分布收敛于N(0,σ2).

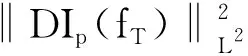
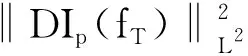
命题2.2的证明：因为

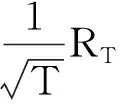
由式(4)知，

(9)

式 (9)等号的右边第一项将依概率收敛于0，因为当T趋向于无穷大时，

式(9)等号的右边第二项是一个正态随机变量，其均值为0，方差等于

根据文献[12]的定理9.2.8，得到

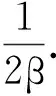
另外，由注2.2知

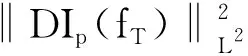
至此，命题2.2得证.

定理1.2的证明：根据命题2.1知

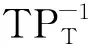
3 结 论

针对一类周期均值回复过程的参数估计问题，假定样本轨道是连续观测的，构造了漂移项中未知参数的最小二乘估计量并讨论了该估计量的统计性质，研究表明该最小二乘估计量具有强相合性和渐近正态性.

参考文献:

[1] 梁晓青,郭军义. 均值回归模型下最优人寿保险的购买和投资消费问题[J].中国科学:数学, 2015, 45(5):623-638.

[2] Geman H. Commodities and Commodity Derivatives[M]. Wiley, Chichester, 2005.

[3] Kutoyants Yu A. Statistical Inference for Ergodic Diffusion Process[M]. Spring-Verlag, London,Berlin, Heidelberg, 2004.

[4] Shimizu Y. Notes on Drift Estimation for Certain Non-recurrent Diffusion Processes from Sampled Data[J]. Stat.Probab.lett., 2009,79(20):2200-2207.

[5] 王银凤. Ornstein-Uhlenbeck 型过程的统计推断和模型选择[D]. 上海: 复旦大学, 2013.

[6] 谢忱. 带线性漂移项Ornstein-Uhlenbeck 过程中轨道滤波估计量的渐近性质[D]. 南京:南京航天航空大学, 2016.

[7] HU Yao-zhong. D Nualart. Parameter Estimation for Fractional Ornstein-Uhlenbeck Process[J].Stat.Prob.Lett.2010(20):1030-1038.

[8] HU Yao-zhong, SONG Jian. Parameter Estimation for Fractional Ornstein-Uhlenbeck Processes with Discrete Observations[J]. Malliavin Calculus and Stochastic Analysis 2013,34(12):427-442.

[9] Bishwal J P. Parameter Estimation in Stochastic Differential Equations[M]. Springer-verlag, Berlin, 2008.24(24):83-94.

[10] Dehling H, Franke B, kott T. Drift Estimation for a Periodic Mean Reversion Process[J]. Stat Inference. Stoch. Process, 2010,13(3):175-192.

[11] Franke B, Kott T. Parameter Estimation for the Drift of a Time-inhomogeneous Jump Diffusion Process[J]. Statistica Neerlandica, 2013,67(2):145-168.

[12] Kuo H H. Introduction to Stochastic Integrals[M]. Springer-Verlag, New York, 2006.

[13] MAO Xue-rong. Stochastic Differential Equations and Applications[M]. second Edition, Horwood Publishing Chichester, UK, 2007.

[14] Nulart D, Ortiz-Latorre S. Central Limit Theorems for Multiple Stochastic Integrals and Malliavin Calculus[J]. Stochastic Process Appl., 2007,118(4):614-628.

[15] Nulart D, Peccati G. Central Limit Theorems for Sequences of Multiple Stochastic Integrals[J]. Ann.Probab., 2005,33(1):177-193.