基于动态时间归整距的地震动特性分析及合成精度评价

何浩祥， 解 鑫， 王文涛

(北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100124)

地震动是复杂的时间-空间随机过程。受震源机制、传播途径、频散效应及场地条件等因素影响，某一点的地震动的频率分布和强度均具有明显时变特征和非平稳性，致使相关的结构地震响应也具有时频非平稳性。此外，由于地震动在空间上也具有强随机性和不均匀性，同一次地震下不同测点的波形特性也有区别，从而导致大跨度结构或多点支撑结构的地震激励和不同位置的响应均具有差异。众多研究表明：幅值(强度)、频谱和持时是表征地震动基本特性的三要素。目前的结构抗震设计和分析主要通过场地类别和地震影响系数来反映地震动的频谱和强度特性，相对宏观和粗略。随着地震工程学的发展，无论是为了准确细致地刻画地震动时频演变特性及不同地震动之间的差异，还是为了评价人工合成地震波或振动台产生的模拟波是否满足规范和工程需求，均需要对强度、频谱和持时进行更精确的量化分析。鉴此，提出能够综合评价不同地震波的波形变化和特性演变的指标具有重要的研究和工程意义。

实际上，在其它领域的研究中也需要甄别不同时域信号的异同，相关方法可统一称为波形相似度评价。适用于区分不同地震波的波形相似度评价指标主要包括峰值偏差、波形相关系数和波形失真度等指标。仅采用峰值偏差来区别不同波形无疑是不够精确的。波形相关系数法采用两个信号卷积的最大值来度量波形相关程度，其计算量大且无法反应信号的局部差异。信号的时域失真度可定义为对比波各点幅值与基波各点幅值残差有效值和基波各点幅值有效值之比。信号的频域失真度可定义为对比信号的各次谐波的能量和与基波总能量值之比。一般认为波形失真度是衡量地震波相似度的首选指标，主要采用位移波形失真度和加速度波形失真度进行评价。虽然波形失真度的物理意义明确、易于计算，但仍然不能全面细致地表征对比波形和基波波形的吻合程度，尤其是对局部随机特性的评价存在误差。因此，亟需提出更精确的波形相似度评价方法和指标。

动态时间规整(Dynamic Time Warping, DTW)算法最早用于处理语音信号识别和分类，其核心思想是将对比信号伸长或缩短，直到与基信号的长度一致，在这一过程中，对比信号的时间轴会产生扭曲或弯折，以便其特征量与标准模式对应，从而进行对比分析。DTW能够计算这两个信号序列的相似程度，并且给出能最大程度降低两个序列距离的点到点的匹配，其匹配和识别效果良好。DTW算法已被广泛应用于诸如动态多变量工业过程的故障诊断、生物基因排序、心电图信号分类等领域[1-2]。

目前研究者已将DTW算法初步应用到地震分析和比较中。Joswing等[3-4]以地震波之间的DTW距作为判断弱局部地震主事件关联性的标准，并利用DTW距来对鲁尔盆地开采诱发地震的位置进行比较和聚类。张博等[5]在动态时间规整的基础上，建立逐步代价最小决策法，并以此作为识别地震与爆破的方法。刘瑞林等[6]利用动态时间规整对相邻地震波进行动态波形匹配并计算波形匹配费用，将波形匹配费用作为相邻地震道波形差异和地层横相变化的度量。董汝博等[7]通过分析合成多点地震动的DTW距离，发现部分点的DTW距离具有奇异性，提出采用内插法合成多点地震动。吴祚菊等[8]基于DTW距离提出了一种有利于大规模时间序列数据挖掘的分段聚合时间弯曲距离，构建了空间多点人工地震动幅值收敛因子。李英民等[9]采用DTW距离代替相关系数作为地震动相似性度量标准，提出了改进的多维相关图法进行地震动非参数研究。然而，以上成果通常只将DTW距作为判定地震动相似或收敛的一种指标，缺少对DTW距基本性能和规律的进一步挖掘，也没有论证地震数据在时空上的非平稳性和分布特征方面与DTW距之间的物理内涵。

鉴此，本文进一步探究了DTW距在地震动中的应用性，提出基于DTW距的地震动波形辨识和地震动特性分析的评价方法，系统考虑时差、幅值、噪信比及时空分布等因素影响下DTW距变化规律，并将其作为人工生成地震动的评判标准之一。结果表明DTW距能够准确而细致地表征以上因素对地震动的影响并对不同波形的特征和非平稳性进行较精确辨识，从而成为地震动波形相似度评价和波形选优的有效依据。

1 DTW算法

DTW算法是把时间规整和间距测量相结合的一种非线性规整技术，其核心是通过寻找一条有效的路径，来准确计算并测量出两条波各对应时间点之间的距离，从而通过距离来判断两条波之间的相似度，DTW距离越小则相似度越高[10-11]。假设有两条地震波T和R分别有N和M个数据点，且N≠M。n和m分别为两条波中的数据点编号。将T和R的各数据点分别沿坐标系的横轴和纵轴列出，则各个数据点号之间的关系可构成一个网格，网格中的任何一个交叉点(n,m)表示T(n)和R(m)的相交，并且该交叉点的失真度为d[T(n),R(m)],如图1所示。DTW算法是要寻找一条通过各个交叉点的从起始点到终止点的最佳路径，使得该路径上所有的交叉点失真度总和达到最小。

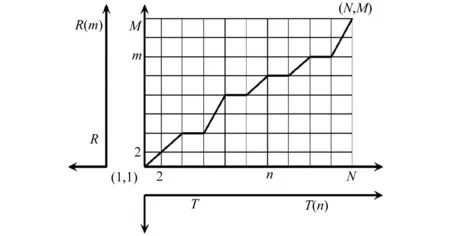
图1 动态时间规整算法求最小失真度Fig.1 Dynamic time warping algorithm for minimum distortion

DTW路径的选择不是任意进行的。首先，考虑到地震动波形具有时间先后顺序，各个部分的次序不能颠倒，因此路径的选择必然从左下角出发，终止于右上角。其次，为了使路径不发生过分的倾斜，对路径中各通过点的路径平均斜率的最大值和最小值加以限制，使得最大和最小值尽量对称分布在斜率为1的对角线两侧，可以约束斜率在0.5～2.0。然后，路径选择是必须考虑所有数据，不可以跳过任何一点。最后，到达任一点(ni,mi)时的前一个点只能是(ni-1,mi)、(ni-1,mi-1)、(ni,mi-1)三点中的一点。此时该点的DTW距离即D(n,m)可用递推公式表示为

D(ni,mi)=d[(T(ni),R(mi))]+

min[D(ni+1,mi)+D(ni+1,mi+1)+D(ni,mi+1)]

(1)

通过递推公式，即可求得从起始点到终止点的最佳路径，从而得出两波形之间的DTW距。由上分析可见，利用DTW距对地震动波形进行相似度检验和波形特征评价是可行的。为了检验DTW算法的精度，本文选取两条典型的地震波进行计算，时间间隔均为0.02 s，主要分析前10 s的数据。图2为两条波的动态

图2 两条典型地震波的动态规整路径图Fig.2 Dynamic regular path of two typical earthquake waves

规整路径图，图中白色曲线即表现出计算过程中最佳路径的选择过程，DTW距为12.97，可见该算法消除了弯折现象对距离测度的不良影响，能有效处理局部时间位移，最终得出合理的匹配结果。如果将其中一条地震波局部峰值部分进行调换，并以原波为基准计算DTW距，获得的DTW路径参见图3，此时DTW距为7.15，相对较小。可以看出当两条波的局部波形相同时DTW路径是一条直线，而对调部分的路径则变成了曲线，该结果展现了DTW算法在选择最佳路径时的一个动态过程，且DTW距和路径对波形的改变是敏感的。以上研究表明将DTW距作为地震动波形相似度评价的指标是相对准确和客观的。

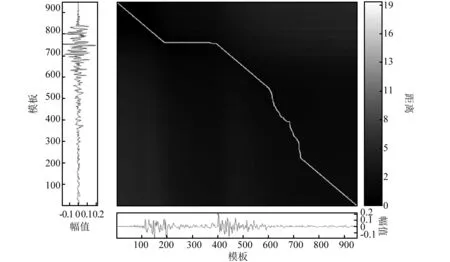
图3 同一条地震波部分调换后动态规整路径图Fig.3 Dynamic regular path of the same wave after partial exchange

2 基于DTW的地震动波形特征评价

地震动的特性一般可以通过幅值、频谱和持时这三个基本要素来描述。对于不同的地震动，当此三要素仅在极值或整体界限上有所区别时相对容易进行辨识和特征评价。然而，当此三要素均发生变化或在局部出现差异时，相似度评价的难度剧增。对于天然地震动，在相似场地条件下获取的地震波蕴含着类似的机理和变化规律，但其随机性和非平稳性往往掩盖了内在的相似性，需要对数据进行深入挖掘。在人工地震动合成中，由于算法本身存在不足而不能充分反映地震动真实特征，加之随机噪声的引入，评价不同合成方法的精度以及同一方法随机生成的不同模拟波形的相似度亟需准确而稳定的方法。当使用地震模拟振动台进行结构动力试验时，控制系统的误差不仅会导致台面输出波与原波的幅值不同，还会混入噪声并产出迟滞现象，判断台面波是否满足精度要求也需要良好的波形相似度评价方法[12-13]。如前所述，利用DTW距进行波形相似度评价具有良好效果，应该可以对不同波形的幅值比例、行波效应(时差)、噪声水平和局部变化特性等进行全面而细致比较，是较理想的波形相似度辨识指标。因此，基于DTW距探究以上因素对地震动特性的影响规律是很有必要的。为了得到相关规律，本文对天然地震动数据进行DTW统计分析，首先分别研究各要素影响下的DTW距变化规律，进而研究考虑综合效益的地震动波形相似度评价和和特征辨识标准。具体分析时，从PEER地震动数据库[14]中选取典型的40条加速度波作为样本，其中四类场地各取10条地震波，时间间隔均为0.02 s，对各因素影响下的DTW距变化规律进行统计分析。

2.1 地震动幅值与DTW距的关系

为了研究加速度峰值对两地震波的DTW距的影响，从上述40条地震波中任意选取了两条地震波数据w1和w2，首先将两条地震波数据均进行归一化处理，将归一化后的w2乘以不同的幅值放大系数得到不同的波形，再计算各波形和w1之间的DTW距，典型的结果如图4所示。从图4可知，地震动幅值与DTW距的之间是严格的线性关系，且幅值对DTW距的影响十分显著。因此对于同一地震动可根据线性关系直接计算出不同幅值放大系数下的DTW距。此外，该结果也表明当需要比较除幅值之外的因素对地震波的影响时，应将各地震波的幅值调成一致方能进行评价。

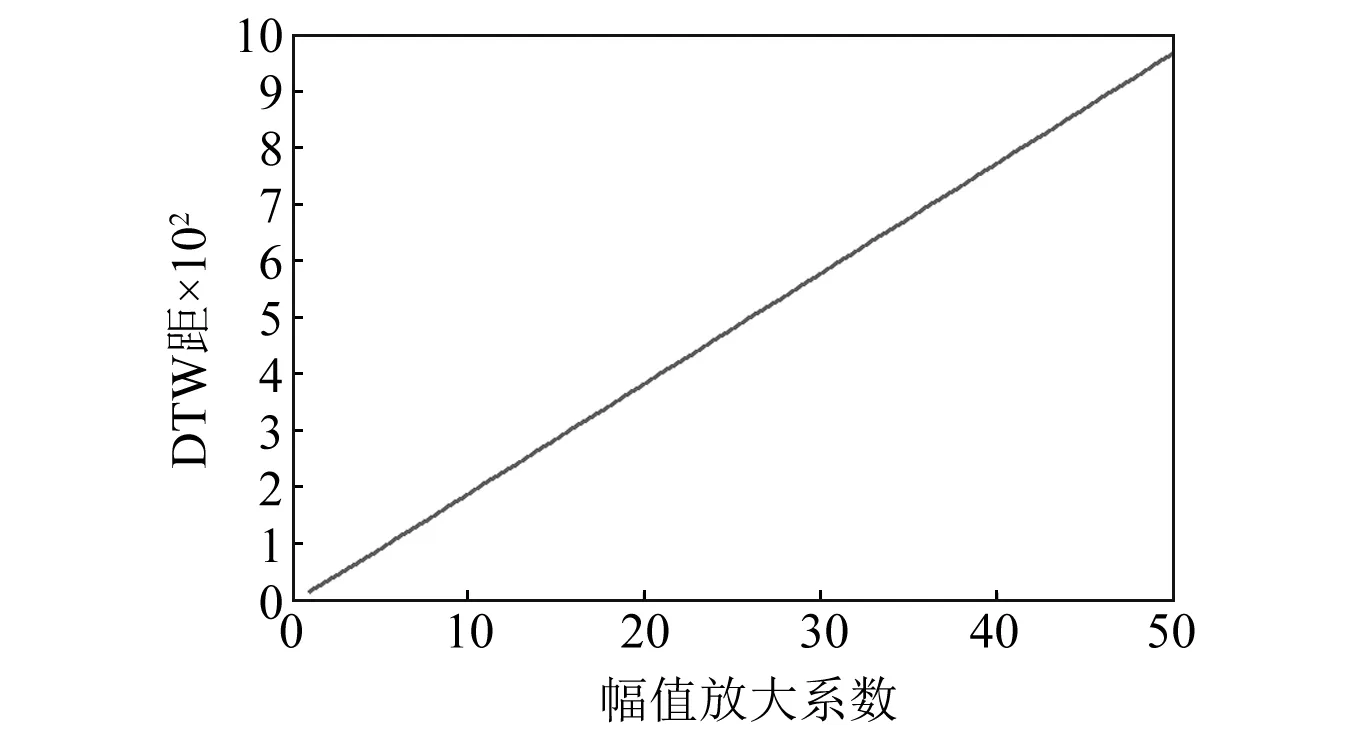
图4 DTW随地震波幅值变化图Fig.4 Variation of DTW with seismic amplitude

2.2 考虑行波效应的DTW距统计分析

为了得到行波效应(时差)影响下的DTW距的统计规律，首先对40条地震波进行归一化，从而排除地震波幅值对DTW距的影响。之后在数据起始点逐渐增加零值数列从而增大时差，得到四类不同场地类型上行波效应影响下的DTW距，如图5所示。其中μ为均值，σ为均方差。全部地震波的DTW距均值μ随时差的变化曲线，如图6所示。由图6可知，时差对地震波的DTW距的影响是随机的，近似于线性，且影响程度较弱。

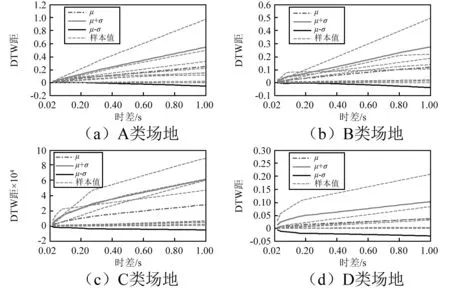
图5 四类场地土上DTW随时差变化图Fig.5 Variation of DTW with time difference for different sites

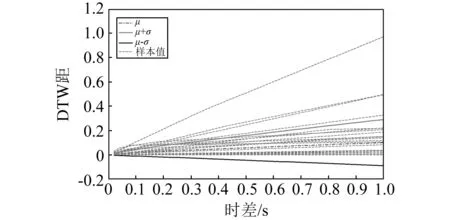
图6 DTW距随时差变化图Fig.6 Variation of DTW with time difference

2.3 考虑噪信比的DTW距统计分析

虽然噪声不会改变地震波的总体变化趋势，但能够使地震波局部发生突变，从而导致两条原值相同地震波之间的DTW距也有所区别。为了得到噪信比(噪声幅值与信号幅值之比，信噪比为其倒数)影响下DTW距的变化规律，对选取的40条地震波进行归一化处理，并生成等长的标准正态分布白噪声。设噪信比为白噪声最大幅值与归一化地震波最大幅值之比，将具有不同强度的白噪声其叠加到归一化地震波中，形成具有不同噪信比的地震波。对于不同的地震波，计算考虑不同噪信比的新波与原波之间的DTW距，所有结果如图7所示。从图7可知，DTW距与噪信比呈近似线性关系，且噪信比对DTW距的影响较明显。图8为DTW距随噪信比的统计值分布图，由此可进一步确定考虑不同噪信比下DTW距的合理取值范围。

图7 噪信比影响下DTW距变化图Fig.7 Variation of DTW distance with different noise to signal ratio

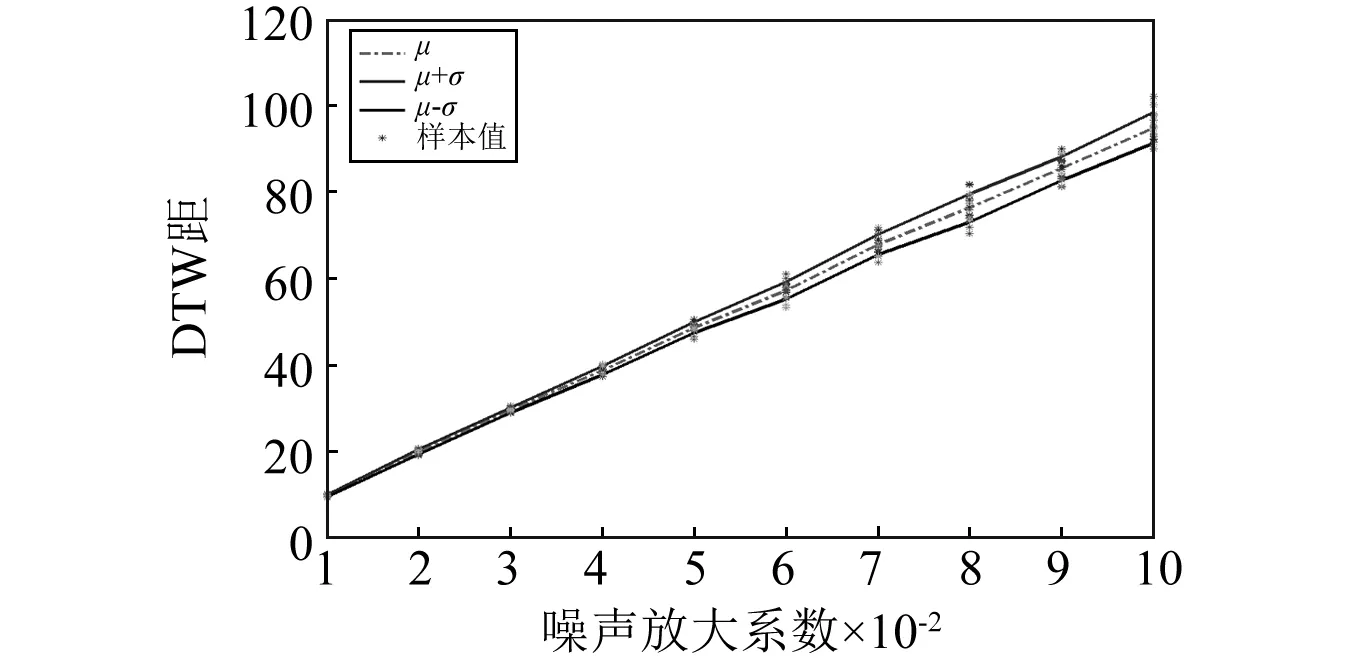
图8 DTW距随噪信比的统计值分布图Fig.8 Statistical distribution of DTW distance with noise

2.4 综合考虑时间差和信噪比的DTW距三维统计分析

实际的地震动差异是由多种因素综合决定的，因此无论是比较不同真实地震动的差异还是评价模拟地震动的精度，都不能只考虑单一因素的影响。由于幅值对DTW距的影响最为显著，其关系十分明确，且该效应可直接识别，因此研究者更关心的是波形变化和细节差异。有鉴于此，本文同时考虑时差和信噪比的影响，针对40条归一化地震波求出不同时差和不同噪信比下相互之间的DTW距，得到DTW距统计均值的三维曲面图，如图9所示。从图9可知，综合考虑时差和噪信比的DTW距的分布基本在一斜平面上，且具有明显的规律性。

对于人工合成或振动台产生的地震波，当评价其是否符合真实地震动特性时，一般只考虑是否满足反应谱和功率谱的精度等要求。实际上，由于地震波的幅值已经由工程需求确定，研究者更关心的是波形的变化特性和规律，但一直缺乏有效的评价指标。因为图9的结果是由大量真实地震动获得的统计均值，且其数值和范围是稳定的，所以可将DTW距作为波形精细化评价的标准。在评价中，可通过计算归一化后的生成地震动与多个典型的归一化真实地震动之间的DTW距均值，并结合图9来判断波形精度是否满足要求，如果所计算的DTW距超过了允许时差和信噪比范围内的DTW参考值，则不建议使用该生成波而需要重新生成和择优。在人工合成地震动精度评价时，可以仅考虑噪信比的影响，因此也可以直接以图8的结果作为评价参考值。当评价振动台产生的地震波是否满足精度时，由于附加噪声和迟滞现象都可能产生，因而需要严格以图9的结果作为评价标准，且可结合DTW路径进行波形细节比较。

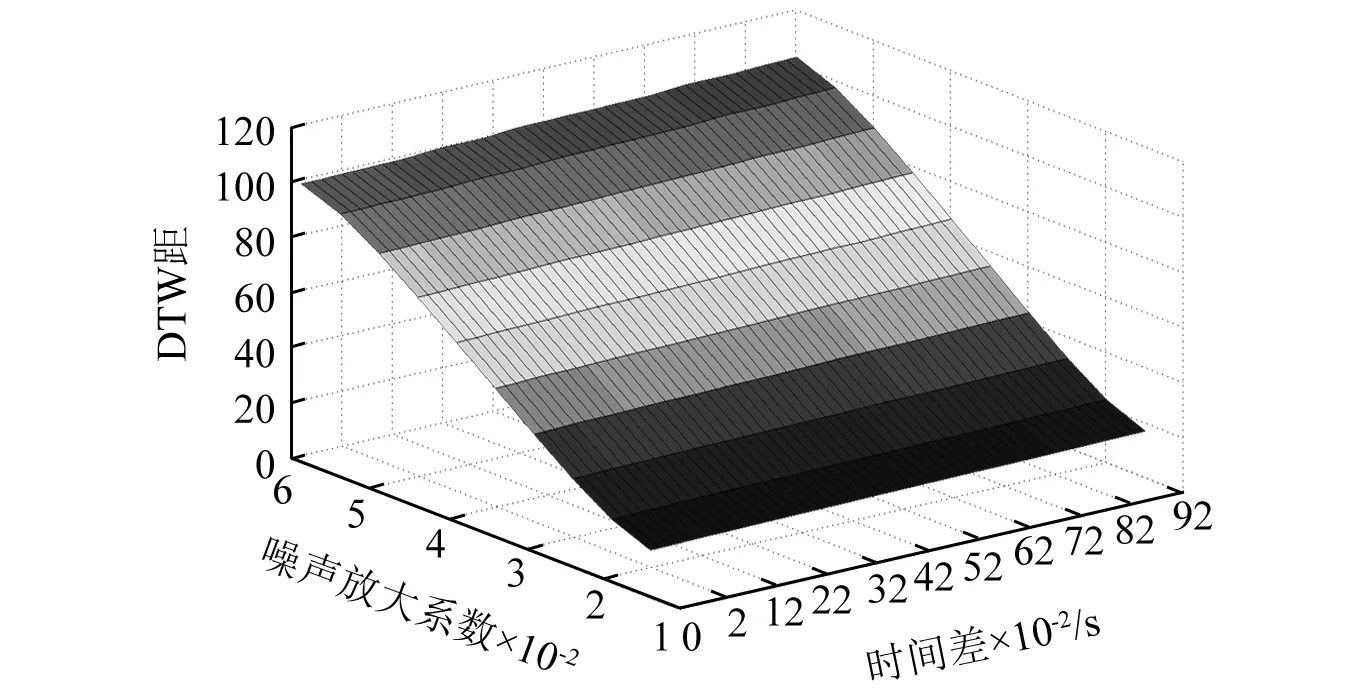
图9 综合考虑时差和噪信比的DTW三维分布图Fig.9 Distribution of the DTW withtime difference andnoise

3 基于DTW距的台阵地震动空间变化效应

在上述研究中，各条地震波是分别从不同地震记

录中独立选取的，由此计算得到的DTW距也不直接相关，相应的结果适用于通常的地震动波形评价。对于某一次地震，小尺度区域的地震动具有类似的路径和场地条件，其衰减特性也相近，因此由地表上不同测点记录到的波形既有区别又有联系，体现了时间-空间变化效应。该效应对大跨结构和桥梁有重要影响，因此在对大跨结构和桥梁进行地震动力分析时需要真实而细致地体现地震动的时空演变特征和规律。为了检验DTW距能否反映地震动时空变化特征以及其作为多点地震动和地震动场规律的评价指标的能力，需要对实际台阵的强震观测数据进行分析。

我国台湾的SMART-1(Strong Motion Array in Taiwan-1)台阵是1979年开始布设的高密度台阵，包括一个中心台站测点(C-00)，36个均匀分布在三个半径分别为200 m,1 000 m和2 000 m的同心圆圆周上的台站测点和延伸线上的2个台站测点[15-16]。SMART-1 台阵测点分布,如图10所示。除了延伸线上的2个台站测点外，所有台站测点均布设在冲积土场地上，所以本文选取除2个延伸测点外的其他测点作为有效测点。

本文选择以往台阵记录中具有代表性的Event 40的地震动数据(南北向)，以最接近震源的O07点为基准点，计算出其它各测点与基准点之间的DTW距，分别将外环(首字母为O)、中环(首字母为M)和内环(首字母为I)的各测点的加速度DTW距画于极坐标图中并做连线，结果如图11所示。按照类似方法，将相应各测点的位移DTW距画于极坐标图12中。从图12可知，靠近震源的各测点DTW距更能反映不同地震波的衰变特征，各环的加速度DTW距分布并不规则，除了在西北方向均具有衰减之外，在其他方向的随机性较明显。各环的位移DTW距分布相对更加有规律性。

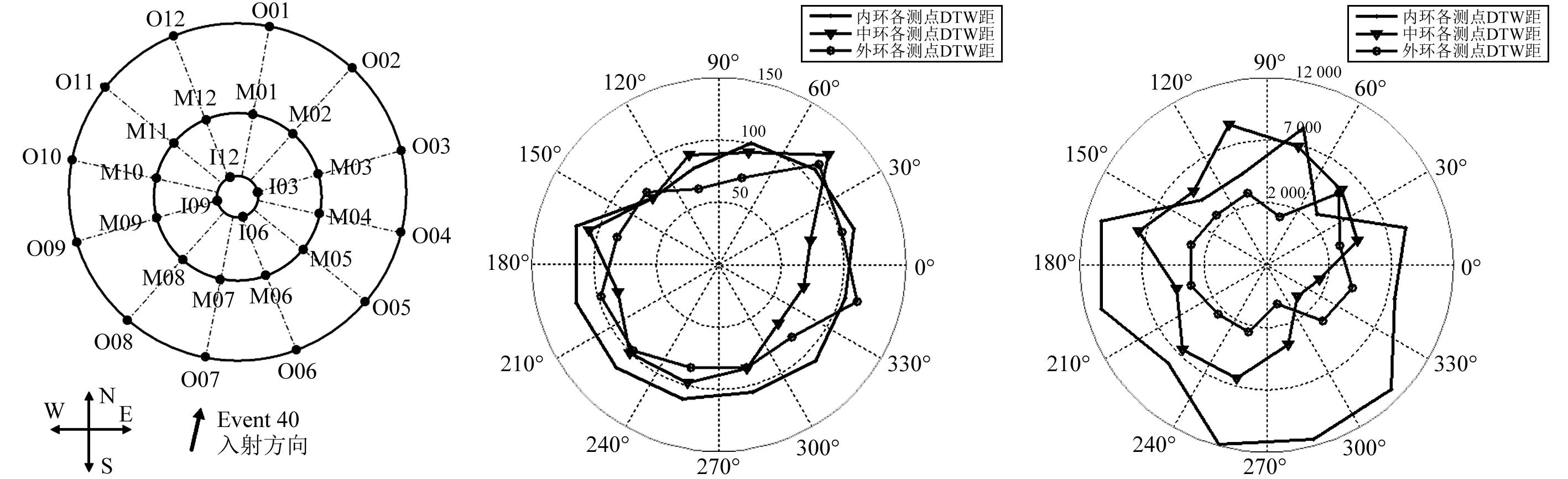
图10 SMART-1台阵测点分布 图11 各测点加速度DTW距 图12 各测点位移DTW距 Fig.10 Array measuring points Fig.11 Acceleration DTW distance of Fig. 12 Displacement DTW distance of distribution of SMART-1 each measuring point each measuring point

下面进一步探究DTW距的物理内涵。根据DTW算法原理可知DTW距实际是波形从起始点到终止点的最佳路径距离之累积和，而范数是对当前向量在空间的一种长度度量，因此可认为DTW距具有与向量范数相似的数学含义。加之DTW距恒大于等于0且与地震动幅值具有线性关系，因此从向量范数角度可认为其具有正定性和齐次性。由于信号的绝对值之和为1-范数，而信号的能量(平方和求和)的方根是2-范数，根据范数等价性原则，DTW距应与以上两种范数即信号的等效幅值和能量密切相关。为了验证上述设想，分别计算各测点的位移波绝对值之和、速度波绝对值之和以及加速度波绝对值之和，并进行综合比较和分析。外环、中环和内环各测点的结果，分别如图13～图15所示。

综合对比图11～图15的结果可知：各测点加速度DTW距分布特征与各测点地震波的加速度绝对值之和分布极为相似，且兼有位移绝对值和与速度绝对值和的部分特征。各测点位移DTW距分布特征与各测点地震波的位移绝对值之和分布也十分相似。

图13 外环各测点的四种值变化Fig.13 Variation of four values of the outer circle

图14 中环各测点的四种值变化图Fig.14 Variation of four values of central circle

图15 内环各测点的四种值变化Fig.15 Variation of four values of the inner circle

由此可以推断：各物理量的DTW距实际上能够表征相应物理量时域信号的等效幅值和能量，且可以反映不同地震波时差和传播特性的综合影响，而DTW距的分布能够在整体上反映地震动时空变化特征。因此将DTW距作为多点地震动和地震动场时空演变规律的有效评价指标是合理的。

4 基于DTW距的人工地震动空间变化效应和精度评价

在地震动合成研究领域，国内外学者进行了大量工作，众多优良的合成方法被相继提出[17-18]。由于地震动合成主要为结构抗震设计和分析提供基础数据，目前大部分方法是以合成与设计反应谱和功率谱相吻合的地震波为目标的，且要对原始波形乘以时域包络函数以保证地震波非平稳性。近年来的研究表明地震动的随机特性是由幅值谱和相位差谱共同决定的，基于相位差谱的合成地震动能够更真实地反映地震动非平稳性。此外，考虑到地震动场的空间变化效应(包括行波效应、部分相干效应和局部场地效应)，尚需根据相干函数理论模型进行对于多点地震动的合成。由于随机模拟合成的地震动通常不能全面而准确地反映真实地震动的时频非平稳特征，加之各种理论和方法固有的特点和局限，各种地震动合成方法的精度并不统一。无论是评价不同方法的精度还是同一方法随机生成的不同模拟波形的相似度，均需要准确而稳定的评价标准，以便进一步选择更真实可靠的地震动。基于DTW距的波形评价为上述问题提供了较好的解决工具。

4.1 基于DTW距的人工地震动精度评价

对于合成地震动生成方案的评价，可以通过判断不同合成方案的DTW距精度是否满足要求来实现，因此需要确定DTW距精度评判标准。本文选取前述40条地震波，计算相互的DTW距离，得到780个不同的DTW距，通过统计其均值和标准差来确定合理的DTW距离精度评价标准，并以均值±0.5倍的标准差作为合成地震波的合理DTW距范围，以均值±1倍标准差作为合成地震波的可接受DTW距范围。计算得到合成地震波的DTW距合理范围为[134.9, 287.1]，相应的DTW距可接受范围为[58.9, 363.2]。

相应精度评价标准确定后，通过各种合成方法随机生成多条地震波，计算由每一种合成方法得到的地震波之间相互DTW距并求其均值和方差，将其与上述DTW距范围标准进行比较，以此来评价各地震动合成方法的合理性和准确性。

本文利用地震动模拟软件SEAS[19]中的多种理论模型和合成方法产生人工地震动，合成地震波为地震动场中所选点的加速度时程。将合成方法、相干函数、包络函数和功率谱等四种不同的方法或模型用字母A，B，C，D，E及N等表示，从而形成不同的组合来表示不同的地震动生成方案。表1给出各方法或模型与字母相对应的关系。例如，ABBC表示选择利用包络函数和功率谱生成空间相关非平稳地震动场的合成方法，且将Hao模型作为相干函数模型，包络函数选为Shinozuk模型，功率谱模型为Clough-Pizen模型。

在人工地震动合成过程中，场地类型选择为Ⅲ类，考虑地震动空间变化效应。由各生成方案分别合成10条地震波，计算每种方案的10条地震波之间的DTW距，并计算相应均值，结果如表2所示。分析表中结果可知，相关函数的类型对人工地震波之间的DTW距影响非常小，可以忽略不计，因此只需分析表2中的最后一列整合方案的数据，并与前面统计得到的实际地震波DTW距均值μ、DTW距合理范围[μ+0.5σ,μ-0.5σ]和DTW距可接受范围[μ+σ,μ-σ]进行综合比较，结果如图16所示。

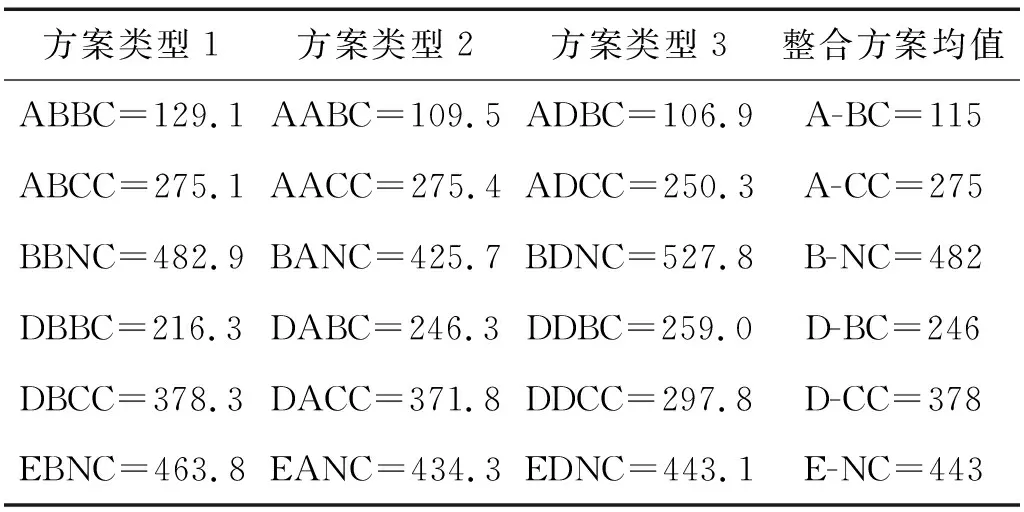
表2 各生成方案对应的DTW距均值Tab.2 The mean value of DTW distance for each generation scheme

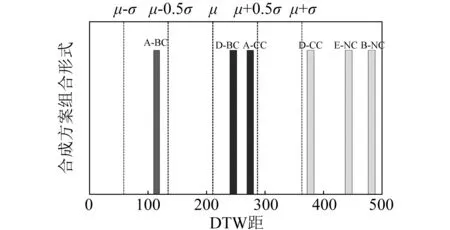
图16 各生成方案DTW距分布范围图Fig.16 DTW distance distribution of each generation scheme

由图16可知，方案D-BC和A-CC在DTW距合理范围[μ+0.5σ,μ-0.5σ]之内，A-BC处于DTW距的可接受范围[μ+σ,μ-σ]之内，而D-CC，B-NC，E-NC的数据则偏离较大处于不合理范围。综上所述，模拟精度较高的地震动生成方案一般均需选择Clough-Pizen模型作为功率谱模型，其他具体方式包括：①合成方法选择利用包络函数和功率谱生成空间相关非平稳地震动场且包络函数模型选择Jennings模型；②合成方法选择空间相关非平稳地震动场基于包络函数的反应谱拟合，包络函数模型选择Shinozuk模型。可接受的生成方案为：合成方法选择利用包络函数和功率谱生成空间相关非平稳地震动场、包络函数模型选择Shinozuk模型。选用其他地震动生成方案可能出现精度不稳定等现象，应谨慎选择和使用。

4.2 人工合成地震动的空间变化效应评价

确定出合理地震动生成方案后，还需要对由同一方案随机生成的不同波形特性进行进一步评价，以便选择更具有典型意义的地震动。当需要合成多点地震动时，还需要确保这些地震动能够反映空间变化效应的基本规律。在考虑空间变化效应的情况下，一般认为如果两条地震波的距离较近，二者的差异较小，相应DTW距也较小；如果两条波的距离较远，二者的差异较大，相应的DTW距也较大。根据前文的研究，尤其是图11和图12的结果，可以认为当生成多点地震动时，随着各点距离的增加确保DTW距也逐渐增加更能够代表地震动时空变化效应的一般规律。因此在从若干个多点合成地震波结果中挑选地震波时，应至少确保一组地震波的加速度DTW距及位移DTW距能够满足上述条件。

下面通过算例进一步说明该要求。设有需要生成地震动的5个点在同一直线上，坐标分别为(0,0),(500,0),(1 000,0),(1 500,0)和(2 000,0)，单位为m。场地类型选择为Ⅲ类，考虑空间变化效应，视波速为1 000 m/s。利用能够得到合理DTW距的生成方案“②”合成3组不同地震波数据，每组各有5条随机地震波。计算各点与原点之间的DTW距，相应的结果如图17和图18(a)～图18(c)所示。从图17～图18可知：生成的3组地震波的DTW距并非全都随着距离增大而递增，因而不能完全体现空间变化效应的基本规律。针对上述问题，本文将地震波重新组合，并计算新组合的5条地震波之间的DTW距，经过调整最终获得满足条件的结果，如图17和图18(d)所示。对于该组地震波，随着各点之间距离的增大，位移DTW距和加速度DTW距均呈递增趋势，故此时更能体现地震动空间变化效应。因此，采用DTW距进行人工地震动的合成精度评价及遴选是更加准确而有效的，能够选出更真实有效的地震动，从而为结构动力分析提供更可靠的激励源数据。

图17 加速度DTW距随各点的距离变化图Fig.17 Acceleration DTW distanceof different points

图18 位移DTW距随各点的距离变化图Fig.18 Displacement DTW distance of different points

5 结 论

利用DTW算法能够计算两个信号的相似程度，并且给出能最大程度降低两个序列距离的点到点的匹配，因此可以采用DTW路径和DTW距实现波形比较和相似度评价。鉴于DTW距能够准确而全面地反映不同地震动波形的差异，本文提出基于DTW距的地震动波形辨识及地震动特性研究的方法。通过对大量典型地震波进行计算分析，分别得到了仅考虑幅值、时差、噪信比和综合考虑时差与噪信比时的DTW距变化规律，验证了可将DTW距作为波形精细化评价的标准。对Smart-1台阵记录中的Event40地震动数据进行统计分析，结果表明DTW距分布情况能够较准确地反映区域内地震动时间-空间变化效应。

(1)基于DTW距的物理意义并结合向量范数的数学含义，阐述了DTW距与向量范数在本质上是等效的，并进一步认为在地震动分析中DTW距与信号的等效幅值和能量密切相关，其分布规律类似。通过台阵数据分析验证了以上观点。

(2)基于DTW距对人工地震动的精度和空间变化效应进行评价，通过计算大量地震波之间相互的DTW距和统计参数，确定了合理的DTW距范围和可接受的DTW距范围，并以此作为合成地震动的精度评价标准。分析结果证明DTW距可以作为多点地震动和地震动场演变规律的有效评价指标。此外，也通过对人工合成地震动中的不同合成方法、相干函数、包络函数和功率谱模型进行组合和对比分析，确定了能够获得更真实特性的人工合成地震动的方法。

(3)对于能够体现基本的地震动空间变化效应的地震波组合，其DTW距应随距离的增大呈递增趋势。由于随机选取的地震波不能充分体现上述规律，因此可将DTW距的变化规律作为依据对多条成地震波进行重新组合和评价，实现具有空间变化效应的人工地震动的合成精度评价及遴选。本文提出的相关方法也可为其他领域的信号分析和波形相似度评价提供参考。

参 考 文 献

[ 1 ] HAN T, LIU X, TAN A C C. Fault diagnosis of rolling element bearings based on multiscale dynamic time warping [J]. Measurement, 2016, 95:355-366.

[ 2 ] ZHEN D, WANG T, GU F, et al. Fault diagnosis of motor drives using stator current signal analysis based on dynamic time warping[J]. Mechanical Systems & Signal Processing, 2013,34(1/2):191-202.

[ 3 ] JOSWIG M, SCHULTE-THEIS H.Master-event correlations of weak local earthquakes by dynamic waveform matching [J].Geophysical Journal International, 1993, 113(3): 562-574.

[ 4 ] SCHULTE-THEIS H, JOSWIG M. Clustering and location of mining induced seismicity in the Ruhr Basic byautomated Master Event comparison based on dynamic waveform matching (DWM)[J].Computers & Geosciences, 1993, 19(19): 233-241.

[ 5 ] 张博, 边银菊,王婷婷. 用逐步代价最小决策法识别地震与爆破[J]. 地震学报, 2014, 36(2): 233-243.

ZHANG Bo, BIAN Yinju, WANG Tingting. Identification of earthquake and explosion by using the method of stepwise cost minimization [J].Acta Seismologica Sinica, 2014, 36(2): 233-243.

[ 6 ] 刘瑞林, 杨峰平, 信毅. 动态波形匹配预测火山岩地层的横向变化[J]. 地球物理学进展, 2004, 19(4): 946-952.

LIU Ruilin, YANG Fengping, XIN Yi. Prediction of the lateral variation of volcanic rock formation by dynamic waveform matching [J].Progress in Geophysics, 2004, 19(4): 946-952.

[ 7 ] 董汝博, 周晶, 冯新. 一种考虑局部场地收敛性的多点地震动合成方法[J]. 振动与冲击, 2007, 26(4): 5-21.

DONG Rubo, ZHOU Jing, FENG Xin. Multi point ground motion synthesis method considering local site convergence [J]. Journal of Vibration and Shock, 2007, 26(4): 5-21.

[ 8 ] 吴祚菊, 张建经,王志佳. 空间多点人工地震动幅值收敛性研究[J]. 振动工程学报, 2015, 28(4): 610-617.

WU Zuoju, ZHANG Jianjing, WANG Zhijia. Research on convergence of dynamic amplitude of multi point artificial earthquake in space [J].Journal of Vibration Engineering, 2015, 28(4): 610-617.

[ 9 ] 李英民, 吴哲骞,陈辉国. 多维标度法在地震动空间特性分析中的应用[J]. 土木建筑与环境工程, 2012, 34(5): 6-11.

LI Yingmin, WU Zheqian, CHEN Huiguo. Application of multidimensional scaling method in the analysis of spatial characteristics of ground motion [J].Journal of Civil,Architectural and Environmental Engineering, 2012, 34(5): 6-11.

[10] FORESTIER G, LALYS F, RIFFAUD L, et al. Classification of surgical processing using time warping [J].Journal of Biomedical Informatics, 2011, 45(2): 255-264.

[11] GOLLMER K, POSTEN C. Supervision of bioprocesses using a dynamic time warping algorithm [J].Control Engineering Practice, 1996, 4(9):1287-1295.

[12] 郭继峰, 任万滨,康云志, 等. 电动振动台模型辨识方法及其应用的研究[J]. 振动与冲击, 2011, 30(7): 241-244.

GUO Jifeng, REN Wanbin, KANG Yunzhi,et al. Research on identification method and application of electric vibration table model [J]. Journal of Vibration and Shock, 2011, 30(7): 241-244.

[13] 栾强利, 陈章位,徐进荣, 等. 地震模拟振动台三参量控制技术研究[J]. 振动与冲击, 2014, 33(8): 54-60.

LUAN Qiangli, CHEN Zhangwei, XU Jinrong, et al. Research on three parameter control technology of earthquake simulation shaking table [J]. Journal of Vibration and Shock, 2014, 33(8): 54-60.

[14] Pacific Earthquake Engineering Research Center. Technical report for the PEER ground motion database web application [EB/OL].(2010-10-01)[2016-11-10]. http://peer_berkeley_ground_motion_database /Technical.Report.pdf．

[15] HAO H, OLIVEIR C S, PENIZEN J. Multiple-station ground motion processing and simulation based on smart-1 array data [J]. Nuclear Engineering and Design, 1989, 111(3): 293-310.

[16] 田利, 李宏男, 侯和涛. SMART-1台阵地震动激励下输电塔线体系反应分析[J]. 工程力学, 2013,30(增刊1):273-283.

TIAN Li, LI Hongnan, HOU Hetao.Response analysis of transmission tower line system under SMART-1 platform vibration excitation [J].Engineering Mechanics, 2013,30(Sup1):273-283.

[17] BERNDT D J, CLIFFORD J. Finding patterns in time series: a dynamic programming approach [M]. Menlo Park: American Association for Artificial Intelligence, 1996.

[18] SARAGONI G R, HART G C. Simulation of artificial earthquakes [J]. Earthquake Engineering & Structural Dynamics, 1973, 2(3): 249-267.

[19] 杨庆山, 田玉基. 地震地面运动及其人工合成[M]. 北京:科学出版社, 2014.