土木工程结构保性能PID协调分散控制研究

潘兆东， 谭 平， 周福霖

(1. 东莞理工学院 建筑工程系， 广东 东莞 523808； 2. 广州大学 工程抗震研究中心，广州 510405)

建筑结构采用主动/半主动等智能控制系统可以显著地抑制其振动响应，从而满足更高的安全和功能要求。其控制思想一般均是采用传统“分散采集，集中处理”的集中化控制方案。然而，对规模宏大、功能多样的复杂工程结构若仍采用传统集中控制，必然会面临如下问题[1]：①控制系统信息交换异常复杂且极易造成滞后；②控制系统集成和运行成本提高；③一旦个别传感器、作动器或者控制平台发生故障，系统的可靠性降低甚至失效等问题。同时，地震、台风等外界荷载及结构自身的不确定性在相当程度上加剧了传统集中控制方案控制效果的波动。

鉴于以上原因，国内外许多学者将大系统分散控制理论引入到土木工程领域，并做了相应的理论研究。文献[2-11]分别基于市场机制、神经网络、瞬时最优、滑动模态、LQG(Linear Quadratic Gaussian)、自适应模糊控制、模糊迭代、LMI(Linear Matrix Inequality)等方法提出了相应的分散控制算法，并通过仿真分析验证了分散控制策略的可行性与优越性。然而，分散控制系统一个显著特点是：控制系统内各分散控制器平行工作，不存在隶属关系，因此难以进行有效的协调；同时，每一个控制器都有自己的控制目标，如果发生冲突则需要用对策论来解决。

因此，本文在分散控制策略基础上提出一种适应于土木工程结构振动控制的协调分散控制策略，在没有中央控制和全局通信的情况下，依靠子控制器和协调控制器对子系统进行协同控制，如图1所示。根据这一思想，建立了协调分散控制系统状态方程。基于线性矩阵不等式方法和PID(Proportional-Integral-Differential)控制理论，给出了保性能PID控制律求解方法，并通过建立和求解一个凸优化问题，设计了能够保证系统性能上届最小的最优保性能PID协调控制器。在此基础上，结合经典极值控制原理，以结构控制效果整体最优为目标设计了子控制器和子滤波器。同时，根据“先分散后协调”设计顺序，利用模拟退火算法对协调控制系统内各子控制器进行优化设计。最后，针对ASCE 9层Benchmark模型，分别进行了集中控制、全维分散控制、部分分散控制和协调分散控制设计、优化与仿真分析。

1 传统集中控制策略

地震激励作用下，n层建筑受控系统动力方程为

(1)

(2)

其中，

2 协调分散控制策略

假设原控制系统分解后存在N个局部子控制器和1个协调控制器，如图1所示。各子系统的控制同时依赖于子控制器分散控制力指令和协调控制器协调控制力指令。这里，协调控制力仅根据协调系统的反馈信息确定，其不受子控制系统的影响。

图1 协调分散控制系统Fig.1 Coordinated decentralized control system

2.1 协调分散控制系统状态方程

根据协调分散控制系统工作原理，协调系统与任一子系统状态方程可表示为

(3)

(4)

式中：zc为协调系统响应向量;Bcc和uc分别为协调控制力位置矩阵与协调控制力向量;Dcc为适当维数的协调系统观测输出矩阵;Bi和ui分别为子系统控制力位置矩阵和控制力向量；Bic为与矩阵Bi对应的协调控制力位置矩阵,Bcc=[B1c,…,BNc]；Di和Dic为具有适当维数的子系统观测输出矩阵。

2.2 保性能PID协调分散控制器设计

2.2.1 保性能PID协调控制器

协调系统受控结构模型建立在原无控结构基础上，同时协调控制器单向作用于子控制器，其不受子系统反馈信息的影响，因此，协调控制器必须具有一定的鲁棒性，这里选择基于线性矩阵不等式方法与PID控制理论设计的保性能PID协调控制器。

将式(3)进一步表示为

(5)

式中：Ac=A;Cc=[I0]n×2n。

在工程实际中，应用最为广泛的调节器控制规律为比例、积分、微分控制，简称PID控制。因此，PID协调控制系统状态反馈控制律可以表示为

(6)

(7)

记Gc=[kpkikd]， 则可建立如下扩阶系统状态方程

(8)

对协调控制系统定义如下二次型性能指标

(9)

对式(8)和式(9)， 如果存在对称正定矩阵P和矩阵Gc，使得

(10)

应用Schur补性质[12]，将式(10)等价为

(11)

(12)

(13)

(14)

结合式(12)和式(13)，协调控制系统控制律可转化为一个凸优化问题

min Trace(V) s.t. 式(12)
式(14)

(15)

则利用式(15)的最优解可以求解出S和W, 根据式(13)即可得到具有性能上届最小的协调控制律。

2.2.2 二次型最优分散控制器

对任一子控制器定义如下二次型性能指标

(16)

式中：Qi为半正定权矩阵;Ri为正定权矩阵。

引入Lagrange函数将式(4)与式(16)的有约束极值问题转化为无约束极值问题，并根据极值存在的必要条件(欧拉公式)，则可通过求解如下Riccati方程得到子控制器的控制增益矩阵Gi。

(17)

协调分散控制系统采用绝对加速度反馈，相应的结构状态信息可以通过设计子Kalman滤波器估计获得，状态估计器方程为

(18)

(19)

式中：Li为子控制器卡尔曼滤波增益矩阵。

3 基于模拟退火算法的控制器优化

图2 SA优化流程图Fig.2 SA optimization flow chart

模拟退火算法(Simulated Annealing Algoritlm， SA)是局部搜索算法的扩展，它不同于局部搜索之处是以一定的概率选择领域中的最优值状态。算法源于对实际固体退火过程的模拟，即先将固体加温至充分高，再逐渐冷却。因此，算法实际上是将优化问题类比为退火过程中能量的最低状态，也就是温度达到最低点时，概率分布中具有最大概率(概率1)的状态[13]。

SA主要参数计算公式

(20)

式(20)为修正的Boltzmann接受概率计算公式。 ΔE为优化目标差；Ts和Tf分别为模拟退火过程的初始温度和终止温度;Ps和Pf为初始和终止温度可能接受较坏结果的概率。模拟降温方式

(21)

式中：Nc为周期总数;Tn+1和Tn为下一时刻与当前时刻的模拟温度。

(22)

4 仿真分析

4.1 算例模型

选取ASCE设计的9层钢结构Benchmark模型[14]作为仿真算例。采用静力凝聚法对原有限元模型进行降阶，仅保留9个平动自由度。为验证所提出的协调分散控制策略，选择两条远场地震波和一条近场地震波：El Centro波、Hachinohe波和Kobe波地震激励，持时40 s，峰值为300 cm/s2。在结构每层均布置作动器，单个作动器最大出力为800 kN。本文算例中集中控制工况采用LQG控制算法，并利用模拟退火算法对控制器进行优化，取上述地震激励下优化结果的平均值为最优控制器参数，以保证达到最优集中控制效果。原结构简化模型及协调分散控制系统示意图，如图3所示。

为验证协调分散控制策略的优越性，按照子系统不同划分方式设计了两种协调分散控制系统，协调分散1和协调分散2。同时，为便于比较，设计了与之相应的两种分散控制系统，其仅去除图3(b)与图3(c)中的协调控制器，并不改变子系统划分方式，分别记为部分分散1和部分分散2。另外，为了说明设置协调控制器的必要性，设计了全维分散控制，即各子控制器对原结构以层为单位进行独立分散控制。

图3 结构协调分散控制示意图Fig.3 Coordinated decentralized control schematic diagram

为了便于描述，将集中控制、协调分散1、协调分散2、全维分散、部分分散1及部分分散2依次记为：CS，CDCS1，CDCS2，DCS0，DCS1和DCS2。

4.2 控制器优化

为得出一般性结论，控制器最优参数取三条地震波优化结果的平均值。图4为SA方法下集中控制系统优化目标函数(J)的迭代过程和模拟降温过程(T)。从图4可知，SA算法能较快的进入期望解所在范围，在优化后期，随着温度的下降,函数值逐渐靠近全局最优解。模拟退火算法主要参数，如表1所示。

图4 集中控制下优化过程Fig.4 Optimization process of centralized control

NcPsPfΓTTsTf500.70.0010.941 32.803 70.144 8

工况CDCS1和DCS1的各子控制器最优参数相同，α1=12.899,α2=13.081,α3=13.16。工况CDCS2和DCS2的各子控制器最优参数相同，α1=12.255,α2=12.44。工况CDCS1和CDCS2的协调控制器参数Qc=101.5I3n×3n,Rc分别取diag([10-9.310-10.410-10.2510-10.110-9.8510-8.8710-8.710-8.9510-9.45])， diag([10-9.210-10.510-10.410-10.310-10.0510-9.6510-8.710-9.1510-9.6])。全维分散工况各子控制器最优参数，如表2所示。

表2 全维分散控制最优控制参数

4.3 协调分散控制减震效果分析与比较

考虑到篇幅有限，在进行集中控制策略、分散控制策略与协调分散控制策略的减震效果结果分析时，仅以El Centro地震激励下的响应进行绘图及说明本文的分析结果，El Centro波、Hachinohe波和Kobe波地震激励下各工况评价指标平均值，如表3所示。

表3 结构响应评价指标

El Centro波地震激励下，工况CS，DCS1和CDCS1(见图3(b))的结构顶层层间位移、绝对加速度及作动器控制力时程比较，如图5所示。通过图5(a)和图5(b)中不同工况间的比较可知，CDCS1结构顶层层间位移峰值响应与绝对加速度峰值响应明显小于CS与DCS1下的响应，其中，工况CS，DCS1和CDCS1下结构顶层层间位移峰值分别为：21.5 mm，21.0 mm和20.0 mm，顶层绝对加速度峰值分别为：3.35 mm，3.13 mm和2.9 m/s2；同时，在地震动持时内，协调分散控制下的控制效果均好于分散控制。图5(c)为工况CS，DCS1和CDCS1下结构顶层作动器控制力时程对比曲线，可以看出，较集中控制策略与分散控制策略而言，协调分散控制策略可以获得更为理想的出力时程，且不超过规定限幅，因而结构响应的控制效果有所改善。

图5 结构顶层层间位移、绝对加速度及控制力时程Fig.5 Time history curves: interstory displacement, absolute acceleration and control force of top floor

图6给出了El Centro波地震激励下工况CDCS1所需的控制累积能量时称图，可以看出协调分散控制系统的总控制能量由各分散控制器控制能量之和与协调控制器控制能量两部分叠加所得。其中，分散控制能量占主要成分(65.7%)，这说明在协调分散控制系统设计过程中采用“先分散后协调”这一设计顺序是合理的；同时比较图6中分散控制器与协调控制器的累积能量曲线，可以发现，协调控制器仅在地震动前期向子系统施加较大控制力，进入地震动中后期，协调控制能量则不再显著增加。

图6 协调控制系统累积控制能量图Fig.6 Cumulative control energy history of CDCS

El Centro波地震激励下，集中控制系统(Centralized Control System, CS)、三种分散控制(DCS0，DCS1和DCS2)及两种协调分散控制(CDCS1和CDCS2)的结构各层最大层间位移角减震率和最大绝对加速度减震率，如图7所示。从图7可知，当采用分散控制策略时，除个别层层间位移角控制效果较集中控制有所减弱外，DCS0，DCS1和DCS2较CS而言均获得更好的减震效果；三种分散控制工况中，全维分散控制效果最好，这是因为全维分散对每一个作动器均设置了一个独立的控制器，通过对各子控制器进行优化，可以使得每一个作动器在地震动期间处在最大功效工作状态；而随着子系统内楼层数的增加，子控制器仅能保证子系统内个别作动器发挥最大功效，这一点可以从图8得到验证。但是，全维分散控制系统子控制器个数较多，对于高层结构而言控制成本较高,且不具备实现性；同时，比较DCS1和DCS2，可以发现随着子系统数量的减少，分散控制系统对结构的控制效果也随之减弱。

图7 结构最大层间位移角与最大绝对加速度减震率Fig.7 the vibration decreasing ratio of maximum inter-story drifts and maximum absolute accelerations

当控制系统采用协调分散控制策略时，协调分散控制(CDCS1和CDCS2)的结构响应控制效果较分散控制(DCS1和DCS2)和CS有显著提高，这是由于协调控制器加强了各分散控制器的控制能力，其对各子系统内每一个作动器进行动态协调补偿，使得作动器的出力更加理想，CDCS1和CDCS2各作动器均处于最大功效状态(见图8)。比较协调分散控制与全维分散控制，可以发现，CDCS1和CDCS2较DCS0而言结构层间位移角与绝对加速度减震效果也有所改善。图8为El Centro波地震激励下工况CS，DCS0，DCS1，DCS2，CDCS1和CDCS2各作动器出力峰值。较集中控制与部分分散控制而言，协调分散控制在协调控制器和各子控制器共同作用下使得子系统内各作动器均处于最大功效工作状态。

图8 控制力峰值Fig.8 Maximum control forces

参考Benchmark建筑模型评价指标，表3为El Centro波、Kobe波和Taft波地震激励下各工况结构响应评价指标平均值，其中J1～J3分别为结构层间位移角峰值、绝对加速度峰值、基底剪力峰值，J4～J6分别为层间位移角、绝对加速度、基底剪力范数的峰值，J7为反映结构阻尼耗能自定义的评价指标

(23)

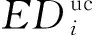
从表3可知，协调分散控制和分散控制各评价指标平均值均表现出与前文所描述结论相似的结果。其中，较工况CS而言，工况CDCS1各评价指标平均值均有较大幅度改善，J1～J7分别提高10%，19%，9%，7%，15%，8%和18%。这是由于传统集中控制仅设置一个中央控制器，而协调分散控制系统则设置了全局协调控制器和多个子控制器，在各子控制器分散控制的基础上利用协调控制器对每个作动器进行动态协调补偿，同时，子控制器之间无需任何信息交流，缩短了信息反馈与控制指令下达的传输时间，减小了时间滞后，从而保证各作动器更加充分地发挥作用，因此，利用最优分散控制器和保性能PID协调控制器设计的协调分散控制策略可以获得更好的减震效果。

5 结 论

本文在结合极值控制、保性能PID控制和分散控制优点的基础上提出了适合于建筑结构振动控制的协调分散控制策略。同时采用模拟退火算法对协调分散控制系统内各子控制器进行优化设计。最后，对9层Benchmark结构进行了集中控制、全维分散控制、部分分散控制和协调分散控制设计、优化与比较分析，仿真计算结果表明：

(1) 协调分散控制能有效抑制结构的地震响应，说明所提出的协调分散控制策略是有效、可行的。不同地震激励下，该控制策略表现出稳定的控制效果，说明其具有较强的鲁棒性。

(2) 依据“先分散后协调”设计顺序，利用模拟退火算法对各控制器进行优化，可以使得协调分散控制系统内各作动器在协调控制器和子控制器协同控制下处于最佳工作状态。

(3) 较集中控制而言，协调分散控制对结构各层层间位移角及绝对加速度的控制效果均有显著提高；由于协调控制器对各作动器的动态协调补偿加强了各子控制器的控制能力，协调分散控制可以获得较分散控制更理想的控制效果。

参 考 文 献

[ 1 ] 席裕庚. 动态大系统方法导论[M]. 北京：国防工业出版社，1988.

[ 2 ] LYNCH J P, LAW K H. Decentralized control techniques for large-scale civil structural systems[C]//Proc. of the 20th Int. Modal Analysis Conference (IMAC XX). Bellingham: Society of Photo-Optical Instrumentation Engineers, 2002.

[ 3 ] XU B, WU Z S, YOKOYAMA K. Neural networks for decentralized control of cable-stayed bridge[J]. Journal of Bridge Engineering, 2003, 8(4): 229-236.

[ 4 ] MONAJEMI-NEZHAD S, ROFOOEI F R. Decentralized sliding mode control of multistory buildings[J]. The Structural Design of Tall and Special Buildings, 2007, 16(2): 181-204.

[ 5 ] LOH C H, CHANG C M. Application of centralized and decentralized control to building structure: analytical study[J]. Journal of Engineering Mechanics, 2008, 134(11): 970-982.

[ 6 ] 李宏男, 李瀛, 李钢. 地震作用下建筑结构的分散控制研究[J]. 土木工程学报, 2008, 41(9): 27-33.

LI Hongnan, LI Ying, LI Gang. Decentralized control of structures under earthquakes [J]. China Civil Engineering Journal, 2008, 41(9): 27-33.

[ 7 ] 宁响亮, 谭平, 周福霖. 公路桥梁振动控制的变论域自适应模糊控制算法[J]. 振动工程学报, 2009, 22(3): 262-267.

NING Xiangliang, TAN Ping, ZHOU Fulin. Vibration control of highway bridge using variable universe adaptive fuzzy control algorithm[J]. Journal of Vibration Engineering, 2009, 22(3): 262-267.

[ 8 ] 汪权, 王建国, 裴阳阳. 地震作用下高层建筑结构的分散模糊迭代学习控制研究[J]. 计算力学学报, 2012, 29(5): 681-686.

WANG Quan, WANG Jianguo, PEI Yangyang. Decentralized fuzzy iterative learning control of tall buildings under earthquakes [J]. Chinese Journal of Computational Mechanics, 2012, 29(5): 681-686.

[ 9 ] 蒋扬, 周星德, 王玉. 建筑结构鲁棒分散控制方法研究[J]. 振动与冲击, 2012, 31(6): 37-41.

JANG Yang, ZHOU Xingde, WANG Yu. A robust decentranzed control method for architectural structures [J]. Journal of Vibration and Shock, 2012, 31(6): 37-41.

[10] 雷鹰, 伍德挺, 刘中华. 一种适用于大型工程结构的分散振动控制方法[J]. 振动工程学报, 2012, 25(4): 411-417.

LEI Ying , WU Deting , LIU Zhonghua. A decentralized vibration control algorithm for large-scale engineering structures[J]. Journal of Vibration Engineering, 2012,25(4): 411-417.

[11] WANG Y. Wireless sensing and decentralized control for civil structures: theory and implementation[D]. Stanford: Stanford University, 2007.

[12] 俞立. 鲁棒控制: 线性矩阵不等式处理方法[M]. 北京：清华大学出版社, 2002.

[13] KIRKPATRICK S, GELATT C D, VVCCHI M P. Optimization by Simulated Annealing[J]. Science, 1983, 220: 671-680.

[14] OHTORI Y, CHRISTENSON R E, SPENCER J B F, et al. Benchmark control problems for seismically excited nonlinear buildings[J]. Journal of Engineering Mechanics, 2004, 130(4): 366-385.